坠落式危岩稳定性计算

高培德，张 刚

(重庆607勘察实业总公司，重庆 400056)

危岩崩塌是石质山区常见地质灾害之一，据不完全统计，崩塌灾害分布在山区铁路上，比滑坡、泥石流更普遍(滑坡、泥石流也属于地质灾害)，约占各类型路基病害总量的半数。以成昆线为例，全线较大滑坡183处，泥石流沟249处、危岩落石近500处，崩塌点约100处[1]。素有山城之称的重庆，境内危岩崩塌点数量多、分布广，其中有代表性的危岩崩塌事件有：重庆武隆鸡尾山崩塌、望霞危岩崩塌和三峡库区的南川金佛山甑子岩崩塌。规模大的崩塌灾害往往威胁人民生命财产安全，阻碍交通建设的发展。因此，重视危岩崩塌灾害，研究防治对策显得十分重要。对危岩崩塌灾害通常的处置手段：首先是对其进行稳定性分析，判别岩石块体的稳定状态，然后针对非稳定、欠稳定块体采取工程治理措施，如：锚固、支撑和清除等，条件允许的情况下还需要对处置后的危岩体做稳定性后评价。岩体稳定性的前期评价关系到后期采取的治理措施以及投资预算等，因此，精确的岩体稳定性分析十分重要。按重庆市地方标准—地质灾害防治工程设计规范(DB50/5029-2004)[2]，危岩稳定性分析计算采用极限平衡方法，将危岩体视为刚体，比较岩体下滑力和抗滑力，获取岩体稳定性系数Fs，但是实际工程中发现采用此方法计算得到的稳定性系数往往不能精确界定岩体稳定状态，这催促我们构建新的计算方法，综合评价岩体稳定性。国内外学者在这方面取得了些许成果，如：李佳壕、吴礼舟认为危岩失稳源自主控结构面的断裂失稳，并运用ABQUS有限元软件绘制了危岩应力强度因子在各因素影响下的趋势图，作为预测危岩失稳的依据[3]；李克森、冯建国结合断裂力学和水力学理论，建立了在渗透力作用下压剪和拉剪复合型危岩主控结构面相当应力强度因子和断裂扩展角的计算方法[4]；于明明等采用悬臂梁力学模型对四川省苍溪县三清村高边坡W1危岩体的稳定性进行了分析和评价，结果与野外宏观判断结论基本一致[5]；何晓英等从能量角度分析了长江巫峡望霞危岩失稳破坏的机制，为危岩崩塌中出现的解体行为与特征提供科学解释[6]；高德福、王亮从静力学着手，分析了楔形危岩块体的破坏机理，并构建了相应的稳定性计算方法[7]；谢立均等分析评价了彭水县某危岩带地质特征以及稳定性，并给出了危岩带防治工程措施[8]；何潇等以望霞危岩为例，从地貌学和力学角度研究了长江巫峡岸坡座滑式危岩稳定性，提出了此类危岩破坏过程的四个阶段[9]。

本文拟在前人研究成果基础上，以坠落式危岩为例，从断裂力学角度，提出危岩稳定性计算新方法，以弥补现有研究的不足。

1 模型建立

野外地质调查发现，坠落式危岩主控结构面多数位于后部，近于竖直；上部为卸荷结构面或断裂结构面，多数处于基本贯通状态，近于水平，如图1示，针对此类危岩体(不去考虑主控结构面位于顶部的情形)，建立如图2所示的物理模型。

图1 坠落式危岩野外实物照片

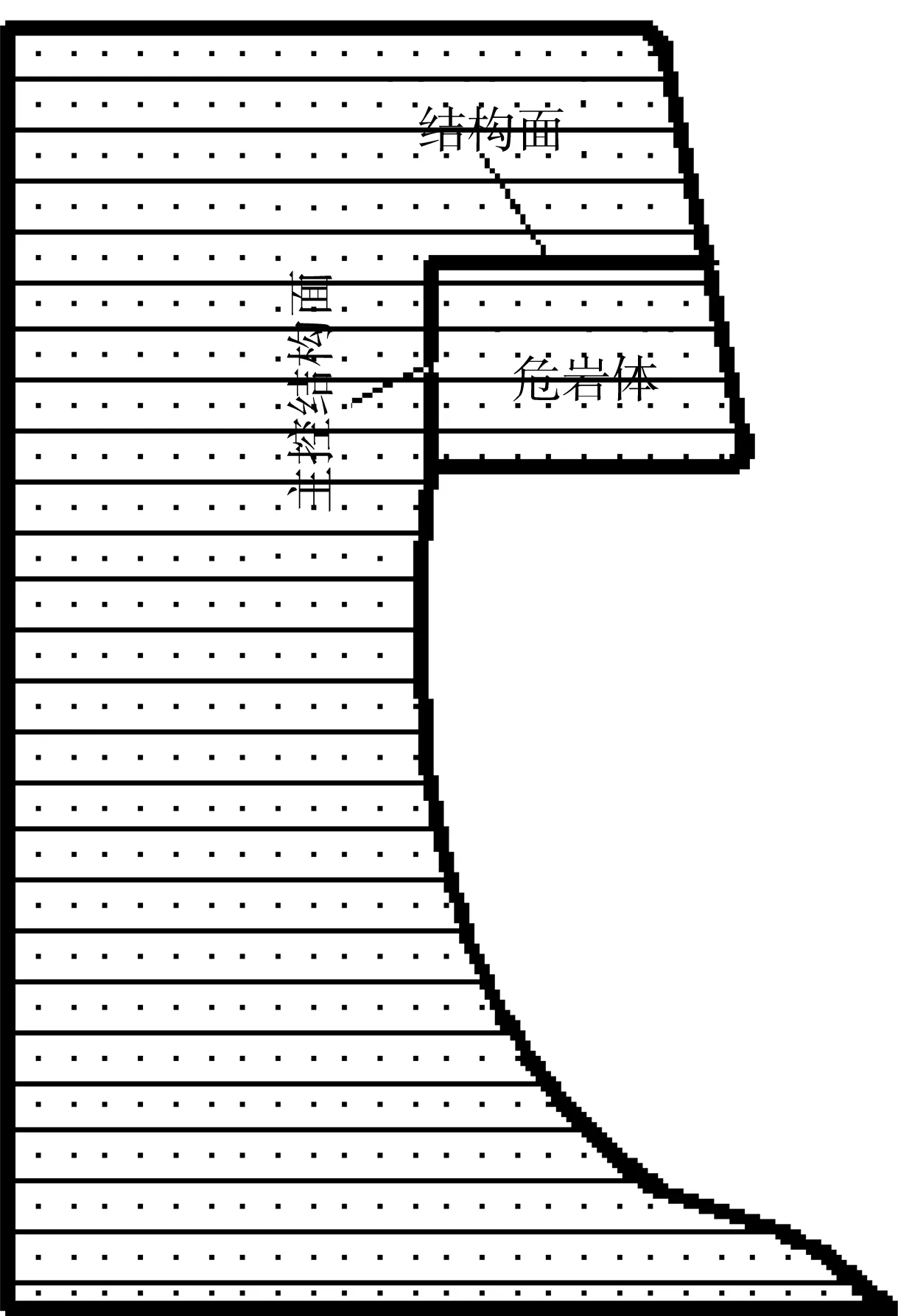
图2 坠落式危岩物理模型

显然，此类危岩体的主控结构面受危岩体自重产生的弯矩和剪力共同作用，从断裂力学角度看，此类危岩体主控结构面端部断裂问题为Ⅰ型和Ⅱ型复合断裂问题，相应的断裂分析模型见图3。

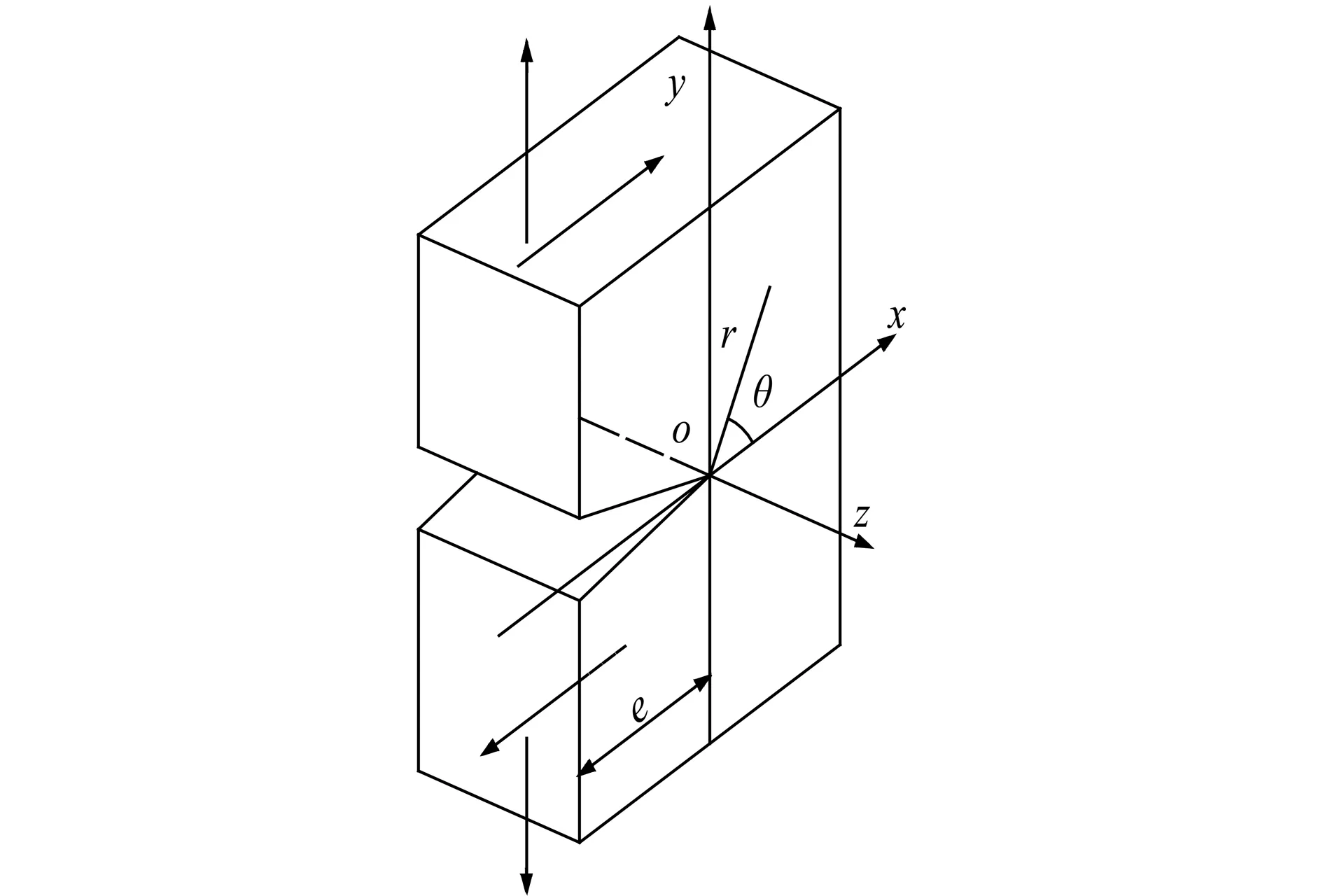
图3 Ⅰ和Ⅱ型复合断裂分析模型

2 模型求解

主控结构面近于竖直的坠落式危岩，其结构面上除受弯矩产生的拉张应力作用外还存在剪切应力的影响，按断裂力学求解方法，我们参考《应力强度因子手册》[10]，分别建立主控结果面端部KⅠ和KⅡ的计算公式。

2.1 应力强度因子KⅠ的求解

应力强度因子KⅠ的贡献主要来源于弯矩产生的拉张应力，其相应计算公式如下：

(1)

(2)

(3)

(4)

式中，F(e)为应力修正系数；σmax为主控结构面所受最大拉应力(kPa)；h为危岩体高度(m)；e为危岩体主控结构面贯通段长度(m)；M为危岩体自重产生的弯矩(kg·m)；W为危岩体自重(kg)；b为危岩体厚度(m)。

2.2 应力强度因子KⅡ的求解

应力强度因子KⅡ的贡献主要来源于主控结构面上所受到的剪切应力，其相应计算公式如下：

(5)

(6)

Fs=W

(7)

式中，τ为危岩体主控结构面所受剪切应力(kPa)；Fs为危岩体主控结构面所受剪力(kN)；l为危岩体主控结构面未贯通段长度(m)。

至此，坠落式危岩主控结构面尖端应力强度因子KⅠ和KⅡ求解完毕。

关于复合断裂问题，迄今为止进行了大量的研究工作，并取得了很大的进展，但是至今未取得完满的结果。目前，关于复合型断裂的理论大致可以分为两类，即应力参量理论与能量理论。属于前者的有最大周向应力理论；而应变能密度因子理论及最大应变能释放率理论等则属于后者。出于简便考虑，本文采用属于应力参量理论的最大周向应力理论(又称σθ准则)建立本研究问题中的断裂分析判据。

按最大周向应力理论，在复合型加载下，裂纹并不一定沿其轴线方向延伸，而可能会出现拐弯现象，发生的这个拐弯角度称为断裂角，断裂角的计算也属于复合断裂分析中要解决的问题之一。裂纹的扩展是沿着最大周向拉应力的截面进行的，这是σθ准则精髓所在，其断裂角θ0满足以下条件：

(8)

(9)

对于Ⅰ、Ⅱ型加载下的平面复合断裂问题，可以根据叠加原理结合极坐标变换得到极坐标形式下的σθ。

(10)

联立式(8)、(9)和(10)得断裂角满足的方程

KΙsinθ0+KΠ(3cosθ0-1)=0

(11)

针对具体问题，根据上式可以求解相应断裂角θ0。仿照Ⅰ型加载下应力强度因子的定义，我们定义一个复合加载下相当应力强度因子Ke

(12)

显然，当相当应力强度因子Ke>KⅠc时，裂纹将开裂扩展，危岩体发生失稳。

3 危岩稳定性的判别及定义

针对本文研究的坠落式危岩，从受力角度来看属于拉、剪型，因此，按断裂力学观点，本文建立的断裂分析模型属于Ⅰ、Ⅱ复合型，并且我们已经根据最大周向应力理论求得了坠落式危岩主控结构面尖端相当应力强度因子的表达式。每一样材料都有达到开裂扩展的临界值，此临界值就是材料的断裂韧性，用表示,组成危岩的材料为岩石材料，因此，使危岩开裂扩展也需要达到开裂扩展的临界值，我们定义危岩断裂稳定性系数Fs为

(13)

按重庆市地方标准—地质灾害防治工程设计规范(DB50/5029-2004)关于危岩稳定性评价标准，对于坠落式危岩：当Fs<1.0，危岩体不稳定；当1.01.5，危岩体稳定。因此，当KⅠc1.5Ke时，危岩体稳定。

至此，坠落式危岩断裂稳定性的判别及定义即建立完毕。

4 总结

本文在前人研究的基础上构建了坠落式危岩断裂稳定性计算方法，现总结如下：

(1)根据坠落式危岩野外实地考察情况，将主控结构面近于竖直的危岩体作为本文研究的主要对象，简化提取了其理论分析的物理模型，并构建了相应的断裂分析模型。

(2)依据建立的断裂分析模型，分别求解坠落式危岩主控结构面尖端应力强度因子KⅠ和KⅡ。

(3)采用复合型断裂判据中的最大周向应力理论研究了坠落式危岩主控结构面尖端裂纹开裂扩展的断裂角，并求解了尖端相当应力强度因子的计算式。

(4)以相当应力强度因子和断裂韧性为基础，定义了坠落式危岩断裂稳定性系数，给出了坠落式危岩稳定状态的断裂参数判别标准。

(5)从断裂力学角度建立坠落式危岩稳定性系数计算方法虽有其新颖性，但暂时只停留在理论层面，未经过实践的检验。

参考文献：

[1]姚一江.危岩崩塌的形成条件、类型及防治原则[J].路基工程,1990,(1):36-39.

[2]DB50/5029-2004重庆市地质灾害防治工程设计规范[S].重庆:重庆市国土资源和房屋管理局,2004.

[3]李佳壕,吴礼舟.危岩应力强度因子的计算研究[J].工程地质学报,2013,21(2):236-242.

[4]李克森,冯建国.考虑渗透力作用的三峡库区危岩失稳破坏机理[J].中国水运,2013,13(5):155-156.

[5]于明明,贾志献,李小雪.基于悬臂梁力学模型分析高边坡危岩体的稳定性—以四川省三清村高边坡W1危岩体为例[J].安全与环境工程，2012，19(1):117-123.

[6]何晓英,陈洪凯,唐红梅.长江巫峡望霞危岩破坏解体特征分析[J].人民长江,2013,44(9):24-28.

[7]高德福,王亮.危岩楔形块体变形破坏机理研究[J].中国新技术新产品:工程技术,2010,(15):119-122.

[8]谢立均,葛明洋,罗鸿.彭水县某危岩带地质特征及稳定性评价[J].西部探矿工程,2014,(3):89-92.

[9]何潇,陈洪凯,赵鹏,等.长江巫峡岸坡座滑式危岩稳定性研究[J].中国岩溶,2013,32(4):411-418.

[10]中国航空研究院.应力强度因子手册[M].北京:科学出版社,1981.