正弦波光栅尺信号的方波相移式细分法及应用*
郑忠杰,陈德传
(杭州电子科技大学自动化学院,杭州 310018)
正弦波光栅尺信号的方波相移式细分法及应用*
郑忠杰,陈德传*
(杭州电子科技大学自动化学院,杭州 310018)
针对正弦波式光栅尺幅值相位细分法中对模数转换处理要求高、软件计算复杂、实时性不强等问题,提出了一种基于方波相移的光栅尺信号检测方法。该方法先将正弦波转换成方波,再从两路方波信号的相对相位位移中提取出光栅尺位移信号,电路简单,软件处理容易,细分精度取决于微处理器主频,对光栅尺信号的正弦近似程度要求不严格。此外,当光栅尺栅距在满足一定条件下与永磁直线同步电机进行一体化设计时,还能直接获得电机动子初始位置。最后,通过实验验证了该方法的可行性,光栅尺的细分精度为0.09μm,直线电机伺服系统的定位控制精度为±0.9 μm。
正弦波式光栅尺;方波相移式细分;相对相位位移;永磁直线同步电机;动子初始位置
永磁直线同步电机能直接将电能转换为直线运动机械能,是高端数控设备中直线驱动控制的关键部件[1]。直线电机能否精确定位,取决于位移反馈元件——光栅尺是否精确。为了提高直线电机的定位精度,一方面是选用更高精度的光栅尺,但这要求提高光栅尺的栅线密度,对工艺要求苛刻,实现起来成本昂贵;另一方面是对普通光栅尺的输出信号进行高倍细分,同样能提高精度,且更具灵活性,实际中更多使用的是这一方案。光栅尺的细分方法有直接四倍频细分[2-3],电阻链细分[4],锁相倍频细分[5],但其中最常用的还属幅值相位细分[6-9],因位移变量隐含在光栅尺输出的正余弦信号的相角中,可通过反正切函数计算出该相角,但此方法对模数转换器的转换速度和精度都有较高要求,软件运行时间长,实时性不强。
本文以横河LM系列永磁直线同步电机内置的正弦波式光栅尺为研究对象,提出了一种基于方波相对相位位移的光栅尺信号检测处理方法,该方法极大程度上降低了对光栅尺栅线密度的要求,又提高了光栅尺信号的细分精度,软件运算简单,且对光栅尺信号的波形正弦近似度要求不严格,当应用于直线伺服系统中时,若光栅尺栅距满足一定条件时,还能直接获得直线电机动子初始位置。
1 系统工作原理
本文所提的基于方波相移的正弦波式光栅尺信号检测处理过程如图1所示,步骤为:(1)对光栅尺输出的8路相位相差45°的近似正弦信号进行严格的同步滤波、跟随后得到信号Vi,再依次通过模拟开关,得到一“调制”信号W0;(2)时钟信号ECLK一方面通过计数器产生模拟开关的地址选择信号,另一方面输出一路8分频后的“载波”信号W1;(3)“调制”信号W0和“载波”信号W1通过高通滤波器消除直流偏置分量,得到两路交流信号X0和X1;(4)两路交流信号X0、X1再通过4阶Butterworth低通滤波器滤去高频分量,得到“调制基波”信号Y0和“载波基波”信号Y1;(5)两路基波信号Y0、Y1再通过高通滤波器、过零比较器和整形电路,得到“调制方波”信号Z0和“载波方波”信号Z1;(6)两路方波信号Z0、Z1最终输入给微处理器,根据它们的相对相位位移变化计算出光栅尺的速度位移。
2 信号检测处理方法
8路光栅尺信号经过同步滤波、跟随后得到的信号Vi表达式为:

(1)
式中,下标i=0,1,…,7,A为信号幅值,w为光栅栅距,x为光栅位移,up为直流偏置。

图2 8路模拟开关和8分频电路
为了得到“调制”信号W0和“载波”信号W1,需进行图2所示电路处理。图2中,ECLK为一固定频率为fclk的方波信号,作为计数器CD4516和CD4024的时钟信号。计数器CD4516的低3位输出端作为模拟开关CD4051的地址选择信号,依次选通V0~V7,模拟开关CD4051的公共输出端再经滤波和跟随器后得到“调制”信号W0;计数器CD4024的第3位输出端作为ECLK的8分频信号输出,经衰减、叠加、滤波和跟随器后得到“载波”信号W1。
“调制”信号W0和“载波”信号W1的波形如图3所示,这是两路带直流偏置的周期性信号,其中信号W0的波形与光栅尺的运动状态有关,信号W1则是固定的波形。

图3 “调制”信号W0和“载波”信号W1

图4 4阶Butterworth滤波器、过零比较和整形电路
图3所示信号不易于分析,为此,还需将信号W0、W1经如图4所示的电路处理。图4中,信号Wi、Xi、Yi、Zi的下标i=0,1,信号Wi先经过高通滤波器滤去直流偏置,得到交流信号Xi;信号Xi经过4阶Butterworth低通滤波器滤去高频分量,得到基波信号Yi;信号Yi再经过高通滤波器进一步滤去由运放输入端偏置所产生的直流分量,最后再经过零比较器、滤波和整形电路,得到方波信号Zi。
先对基波信号Yi进行分析。根据文献[10]可知“调制基波”信号Y0和“载波基波”信号Y1的表达式为:
Y0=A0sin(ω0t+φ0)
(2)
Y1=A1sin(ω1t)
(3)
ω0=ω1-Δω
(4)

(5)

(6)
式中,A0、A1分别是信号Y0、Y1的幅值,一般情况下A0≠A1,φ0是信号Y0、Y1的初始相位差。
根据式(2)~式(6)可以看出,当光栅尺静止时,ω0=ω1;当光栅尺运动方向为正时,ω0<ω1;当光栅尺运动方向为负时,ω0>ω1。这3种情况下信号Y0、Y1的波形如图5所示。图5也表明了基波信号Y0、Y1之间的相对相位位移φ和光栅尺位移x之间的关系,即:

(7)

图5 “调制基波”信号Y0和“载波基波”信号Y1
然而,直接从基波信号Yi中提取相对相位位移φ比较困难。显然,将基波信号Yi转换成方波信号Zi后,其相对相位位移之间的关系保持不变,且方波信号Zi也更易于微处理器处理。
“调制方波”信号Z0和“载波方波”信号Z1的波形如图6所示,其中高频脉冲是微处理器的主频时钟,频率为fosc,Mi是两路信号相邻上升沿之间的高频脉冲个数,下标i=0,1,…,8,并另设N0、N1分别为周期2π/ω0、2π/ω1内高频脉冲个数。

图6 “调制方波”信号Z0和“载波方波”信号Z1
图6(a)中,光栅尺静止,ω0=ω1,显然有M0=M1=M2,若此时为系统刚上电时的状态,那么此时的相位差就是两路信号的初始相位差,即:

(8)
图6(b)中,光栅尺运动方向为正,ω0<ω1。在t6~t8时间段内(即信号Z1的的一个周期内),信号Z0的上升沿与信号Z1的上升沿之间相差了M3个脉冲,在t8~t10时间段内,信号Z0的上升沿与信号Z1的上升沿之间相差了M4个脉冲,则在t7~t9时间段内,信号Z0相对于信号Z1所产生的相位位移为:

(9)
在t9~t12时间段内,存在信号Z1的两个上升沿,说明信号Z0相对信号Z1的相位差从2π→0,此时取信号Z0的上升沿与信号Z1的第2个上升沿之间的脉冲数M6来计算位移,则在t9~t12时间段内,信号Z0相对于信号Z1所产生的相位位移为:

(10)
图6(c)中,光栅尺运动方向为负,ω0>ω1。类似地,在t14~t16时间段内,信号Z0相对于信号Z1所产生的相位位移为:

(11)
在t16~t17时间段内,不存在信号Z1的上升沿,说明信号Z0相对信号Z1的相位差从0→2π,此时取信号Z0的上升沿与信号Z1上一个周期的上升沿之间的脉冲数M8来计算位移,则在t16~t17时间段内,信号Z0相对于信号Z1所产生的相位位移为:

(12)
令微处理器在每个信号Z0的周期内对相对相位位移φ进行更新,则综合式(8)~式(12)不难总结出,相对相位位移的表达式为:

(13)
式中,N(k)是一计数器,当在第k个信号Z0周期内检测到两个信号Z1的上升沿(如图6(b)中的t9~t12时间段),则对N(k)加1;当在第k个信号Z0周期内检测不到信号Z1的上升沿(如图6(c)中的t16~t17时间段),则对N(k)减1。
M(k)则是指在一个信号Z1周期内,信号Z0的上升沿与信号Z1的上升沿之间相差的高频脉冲个数,对应于N(k)有两种特殊情况:(1)若在当前信号Z0周期内检测到信号两个Z1的上升沿,则M(k)取信号Z0的上升沿与信号Z1的第2个上升沿之间的脉冲数(如图6(b)中的M5);(2)若在当前信号Z0周期内检测不到信号Z1的上升沿,则M(k)取信号Z0的上升沿与信号Z1上一个周期的上升沿之间的脉冲数(如图6(c)中的M8)。
最后根据式(7),可知光栅尺位移表达式为:

(14)
进一步可得光栅尺速度表达式为:
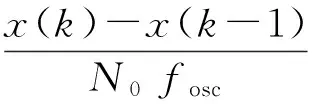
(15)
若忽略实际中的干扰等因素,假设信号Z0、Z1是严格对称的方波,那么理论上光栅尺的细分精度可达w/N1,也就是光栅尺一个栅距w被N1等分,N1的大小取决于微处理器主频fosc。此外,因为是从基波信号中间接提取出光栅尺位移,这也就只要求光栅尺输出信号呈周期性即可,而对其正弦波近似程度要求不高。
3 在直线伺服系统中的应用
在永磁直线同步电机伺服系统中,为了实现矢量控制,都需要事先知道电机动子初始位置,而一般用增量式光栅尺进行动子初始位置定位都比较麻烦[11]。若对增量式光栅尺信号采用前文所提方法处理,那么就可以很容易得到动子初始位置。
设τ是电机极距,θ是动子平移位移折算成的电角位移,则有:

(16)
令w=2τ,则电机产生2π电角位移时所对应的动子平移位移量刚好是一个光栅尺栅距w,而从式(7)可知,当光栅尺产生一个栅距w位移时,信号Z0相对于信号Z1所产生的相位位移也为2π。因此,电机动子位置必然和信号Z0、Z1之间的相位差存在一一对应关系。这样,当系统刚上电电机处于静止状态时,电机的动子初始位置θ0与信号Z0、Z1的初始相位差φ0之间会有如下关系:
θ0=φ0+Δθ
(17)
式中,Δθ是偏移修正角度,为固定常量。
需要指出的是,为了实现动子初始位置定位,必须满足w=2τ,因此此类光栅尺一般都是与相应的永磁直线同步电机进行一体化设计。本文实验所用到的横河LM系列永磁直线同步电机就属于这类电机。
4 实验验证
为了证明本文所述的光栅尺信号方波相移式细分处理方法及其应用的可行性,以横河LM系列永磁直线同步电机的内置正弦波式光栅尺为对象进行了实验验证,实验平台如图7所示。该永磁直线同步电机极距τ=1.037 5 mm,光栅栅距w=2.075 mm,满足w=2τ条件。实验中,时钟信号ECLK的频率fclk=25 kHz,微处理器选用ST公司的STM32F103,主频fosc=72 MHz。

图7 光栅尺方波相移式细分及应用实验平台
实验中光栅尺细分实验的相关波形如图8所示,其中图8(a)为光栅尺运动时发出的两路相位相差45°的信号V6和V7,图8(b)为光栅尺静止时的“调制”信号W0和“载波”信号W1,图8(c)为光栅尺静止时的“调制基波”信号Y0和Y1,图8(d)、图8(e)、图8(f)则分别为光栅尺静止、运动方向为正、运动方向为负时的“调制方波”信号Z0和“载波方波”Z1。仔细观察图8(e)、图8(f)可以发现,当光栅尺运动方向为正,信号Z0的频率变小,与信号Z1的相位差增加;当光栅尺运动方向为负,此时信号Z0的频率变大,与信号Z1的相位差减小。信号Z0相对于信号Z1所产生的相对相位位移变化与图6中的分析一致。

图8 光栅尺细分实验的相关波形
根据磁定位理论[12],当给交流电机施加固定电压矢量时,最后电机动子方向会与电压矢量的方向大致相同。据此,令电机动子处于不同的给定位置P1~P5,再先后施加电压矢量u1和u2,其中u1和u2相差120°,且幅值保证电机电流不超过额定值。当电机在某一电压矢量作用下处于稳态静止时,测得信号Z0与Z1上升沿之间相差的高频脉冲数如表1所示。从表1可以看出,无论电机处于何种位置,在相同电压矢量作用下,最终静止时测得的高频脉冲数变化不大。这5次实验所得数据的平均值相差7 691个高频脉冲,根据式(8)计算出对应的相位差为120.2°。这说明信号Z0与Z1之间的相位差与电机动子的位置存在一一对应关系。因此,只需要进行一次离线计算求出偏移修正角度Δθ,那么之后就可根据式(17)进行动子初始位置定位了。
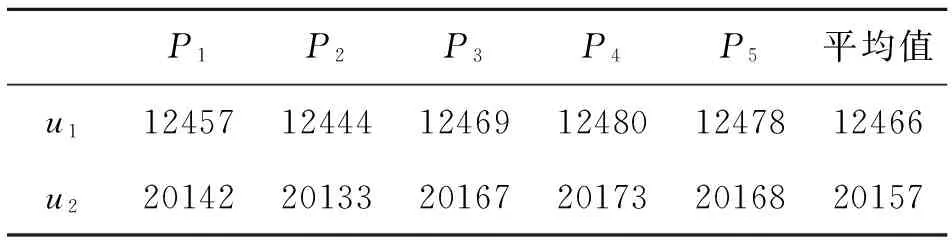
表1 电机静止时信号Z0与Z1上升沿之间相差的高频脉冲数
将光栅尺方波相移式细分方法应用于永磁直线同步电机伺服系统中并进行了位置环控制实验,实验波形如图9所示。图9(a)、图9(b)中,上半部分为位置波形,下半部分为速度波形,可以看出位置响应均十分快速且无超调。这也说明了本文所述的光栅尺细分方法软件处理简单,不会给微处理器造成负担从而影响伺服系统的控制性能。此外,根据前文的分析可得N1=8fosc/fclk=23 040,故光栅尺细分精度为w/N1=0.09 μm,但实际应用中,逆变器会产生干扰,此时实测直线伺服系统定位控制精度为±0.9 μm。

图9 永磁直线同步电机伺服系统运行的相关波形
5 结束语
本文提出了一种基于方波相对相位位移的正弦波式光栅尺信号检测处理方法,分析了其电路和信号特征,并通过实验验证了其可行性。该方法电路简单,对光栅尺信号波形的正弦近似程度要求不高,软件处理容易,无需光栅尺有很高的栅线密度,细分精度取决于微处理器主频。当光栅尺在栅距满足一定条件下与直线伺服电机进行一体化设计时,还能直接获得电机动子的初始位置。目前,该方法已在基于横河LM系列永磁直线同步电机的矢量控制系统中得到应用,光栅尺细分精度为0.09 μm,直线伺服系统定位控制精度为±0.9 μm。若提高微处理器的主频并改善降噪措施,则可进一步提高光栅尺的细分精度和系统定位控制精度。
[1] 郭庆鼎,王成元,周美文,等. 直线交流伺服系统的精密控制技术[M]. 北京:机械工业出版社,2000:1-16.
[2]王成元,常国祥,夏加宽. 新型光栅信号接口IC的设计[J]. 电机与控制学报,2007,11(4):421-424.
[3]Dong Limei,Lu Yuan. The Signal Acquisition System of the Grating Displacement Sensor Based on CPLD and USB Interface[C]//ICIE,Beidaihe,China,2010:185-188.
[4]张兴华,王克逸. 光栅信号电阻链高倍细分法的误差校正的研究[J]. 电子测量技术,2008,31(7):35-39.
[5]罗刚,熊文卓. 光电轴角编码器光电信号正交偏差的测量和补偿方法[J]. 传感技术学报,2008,21(11):1853-1857.
[6]胡晓东,彭琅,雷明,等. 一种光栅细分算法的FPGA实现[J]. 光子学报,2011,40(3):407-412.
[7]刘海龙,贺昱曜,李洁. 麦克劳林级数法求取光电编码器转子位置算法[J]. 传感技术学报,2013,26(5):616-620.
[8]Liu Bo,Li Jinyan. Research on Signal Subdivision of Grating Sensor[C]//IFOST,Harbin,China,2011:1235-1238.
[9]曹卫峰,张梅,文芳,等. 高速高精度光栅位移传感器辨向与细分算法的设计[J]. 组合机床与自动化加工技术,2010,(9):27-33.
[10]Chang Li,Xu Hui,Zhou Yinggang,et al. All Digital Phase Detection and Tracking Method to Subdivide the Grating Morie Fringe Signal[C]//CAR,Bangkok,Thailand,2009:469-472.
[11]腾福林,胡育文,黄文新. 永磁同步伺服系统初始位置修正算法[J]. 中国电机工程学报,2008,28(27):109-113.
[12]黎永华,皮佑国. 基于磁定位原理的永磁同步电机转子初始位置定位研究[J]. 电气传动,2010,40(3):28-31.

郑忠杰(1991-),男,浙江温州人,硕士研究生,研究方向为电机控制与应用,372604194@qq.com;

陈德传(1959-),男,福建福州人,教授级高工,研究方向为电机控制、电力电子系统,chendechuan@hdu.edu.cn。
TheSquare-WavePhase-ShiftSubdivisionMethodforSine-WaveGratingSignalandItsApplication*
ZHENGZhongjie,CHENDechuan*
(School of Automation Hangzhou Dianzi University,Hangzhou 310018,China)
For the problems that the amplitude phase subdivision method for sine-wave grating signal has a high requirement on ADC,a complex software processing,and a weak real-timing,a grating signal detection method based on the phase-shift between suqare waves is proposed. According to this method,sine waves are converted to square waves,and the grating displacement is extracted from the relative phase-shift between the two square waves. The hardware circuit and the software processing are simple,and the subdivision accuracy is depended on the MCU frequency. The strict sinusoidal similarity of grating signal is not required. Moreover,the mover initial position can be directly obtained when the grating is built in the permanent magnet linear synchronous motor under certain condition. Finally,the feasibility of this method is verified by experiments,the subdivision accuracy of grating is 0.09 μm,and the positional accuracy of linear motor servo system is ±0.9 μm.
sine-wave grating;square-wave phase-shift subdivision;relative phase-shift;permanent magnet linear synchronous motor;mover initial position
项目来源:浙江省自然科学基金项目(Y1101143)
2014-06-25修改日期:2014-08-28
10.3969/j.issn.1004-1699.2014.10.024
TP212;TP271.4
:A
:1004-1699(2014)10-1437-06

