生物可降解聚合物血管支架膨胀性能有限元分析

赵 丹 阳, 顿 锁, 田 慧 卿, 王 敏 杰, 于 同 敏, 刘 永 云

( 大连理工大学 精密与特种加工教育部重点实验室, 辽宁 大连 116024 )



生物可降解聚合物血管支架膨胀性能有限元分析

赵 丹 阳*, 顿 锁, 田 慧 卿, 王 敏 杰, 于 同 敏, 刘 永 云

( 大连理工大学 精密与特种加工教育部重点实验室, 辽宁 大连 116024 )

血管支架最有潜力的发展方向是生物可降解聚合物血管支架,而支架的膨胀性能直接影响血管支架的质量和应用．利用有限元方法,采用von Mises屈服和各向同性强化准则,通过与316L不锈钢和WE43镁合金两种支架材料进行对比,分析了聚左旋乳酸(PLLA)材料支架的膨胀性能．结果表明,PLLA新型血管支架具有良好的均匀膨胀性、轴向短缩性和柔顺性,但其回弹性能有待改善．

生物可降解；聚合物血管支架；膨胀性能；有限元分析；各向同性强化准则

0 引 言

随着科学技术的快速发展,血管支架主要经历了金属裸支架和载药支架的发展过程．金属裸支架和载药支架虽然具有优异的力学支撑性能,但由于不能降解,存在诱发血栓和发生再狭窄的缺点,同时还可能存在一些潜在的并发症[1-2]．近几年,国外学者提出了一种生物可降解聚合物血管支架材料,此种材料不仅具有很好的生物相容性,而且可以在一段时间内支撑血管壁并最终降解成二氧化碳和水,避免了血栓的出现和再狭窄的发生,是目前最具有潜力的支架材料[3-4]．由于血管支架的尺寸微小,结构复杂,需要研究血管支架的膨胀过程和植入治疗中支架的弹塑性变形行为,从而进行血管支架的结构优化和材料设计．Chua等研究了支架内压力的增长速度对支架膨胀的影响,发现了低的压力增长速度将会产生理想的扩张直径,但是会造成马鞍形膨胀[5]．Migliavacca等借助有限元方法研究了血管支架的机械特性,指出了低金属覆盖面积比的血管支架具有较高的径向和轴向回弹,但膨胀不均匀系数较低,提出在支架结构优化设计时应该综合考虑以上因素[6]．Pant等利用有限元方法模拟支架的膨胀过程,通过分析支架几何参数与支架的平均应力、回弹性、载药能力和弯曲性之间的关系,优化了支架结构[7]．王小平等利用有限元方法分析了可降解镁合金血管支架的力学特点,通过优化血管支架几何结构,细化镁合金晶粒,提高材料塑性变形能力,设计出了满足延伸率范围的镁合金血管支架[8]．Wang等对血管支架防“狗骨头”设计进行了研究,证实减少球囊的过盈量或增加支架端部支柱的宽度均可以减弱血管支架的“狗骨头”现象,这为球囊-支架系统的设计提供了帮助[9]．目前,血管支架膨胀性能的有限元分析主要针对金属材料,而对生物可降解材料血管支架膨胀过程的研究,国内外未见报道．因此,本文利用有限元分析技术,采用von Mises屈服和各向同性强化准则,通过与316L不锈钢和WE43镁合金这两种支架的膨胀过程进行对比,分析聚左旋乳酸(PLLA)血管支架的膨胀性能．

1 血管支架膨胀过程有限元分析

1.1 几何模型与网格划分

分析对象为一种新型的生物可降解血管支架,其平面结构如图1所示．该血管支架分别沿着周向和轴向对称,模型的几何参数如表1所示．当血管支架植入到病变部位时,在球囊的作用下支架扩张．球囊撤出后血管支架将在自身弹性和血管壁压缩的共同作用下发生高度非线性的回弹,因此血管支架、球囊和病变血管所构成的系统较为复杂,分析难度较大．为了使计算得到简化,只分析血管支架的膨胀过程．由于其对称性,只研究轴向1/2、径向1/2的血管支架．用Pro/Engineer软件建立血管支架的三维几何模型,将模型导入COMSOL系统中进行有限元分析．

图1 1/4血管支架平面结构

表1 模型参数

网格划分是进行有限元分析至关重要的一步,它直接影响着后续计算结果的精确性和计算效率．本文采用自由网格划分的方式,并通过预先定义进行网格细化,既可提高计算精度,同时又能缩短计算时间,网格划分如图2所示．

图2 血管支架的网格划分

1.2 材料参数与模型

由于塑性变形在血管支架的扩张变形中占主导作用,且支架材料特性已经进入到非线性阶段,所以采用von Mises屈服准则和各向同性强化准则作为材料模型．von Mises屈服准则是指材料处于塑性状态时,其等效应力始终是一个不变的定值．各向同性强化准则是指材料进入塑性变形后,屈服面在各个方向均匀扩大,而其形状、中心位置均保持不变．

目前医用金属材料是制造血管支架的主要材料,其中最具代表性的是316L不锈钢和WE43镁合金,它们都具有很好的生物相容性和足够的力学特性,但金属支架在植入人体后可能会引起再狭窄和血栓的发生,同时还会出现潜在的并发症．近年来,发展了一类生物可降解聚合物材料,这类材料具有良好的生物相容性和可吸收性,无全身毒性和细胞毒性,有很好的人体内移植作用[10],其中最具代表性的是PLLA．因此,本文对316L不锈钢、WE43镁合金和PLLA生物可降解聚合物3种材料血管支架的膨胀过程进行模拟,对比分析它们的力学特性．这3种血管支架的材料参数如表2所示[6,11]．

表2 3种血管支架的材料参数

1.3 边界约束条件与求解控制

为了防止血管支架的移动,在支架的膨胀过程中约束径向上的一个点,从而固定其他方向上的刚体位移．为了防止支架发生转动,在支架的对称平面处设置对称边界条件(法向位移为零),如图3所示．

模拟血管支架膨胀时,有位移加载和内压力加载两种方式,但位移加载不能真实反映血管支架膨胀的形式,因此采用内压力加载方式,即在血管支架的内表面加载沿径向向外的压力[12]．冠状动脉血管壁不可能出现屈曲失稳的情况,所以只需考虑血管支架的径向支撑力．根据血管支架的变形特点,采用稳态求解器求解,并通过设置荷载减小到零来模拟血管支架在球囊撤出后的变形过程,获得血管支架的最终稳定形状,整个变形过程采用大变形条件．

图3 血管支架的边界约束条件

1.4 支架变形参数定义

血管支架在介入治疗的过程中通过一个气囊被携带到血管中．当气囊-支架系统到达动脉血管里的预定位置时,通过控制气囊膨胀使支架结构撑开,然后控制气囊泄气并将其移除,扩展开的支架则被保留在血管中的特定位置起到保持血管张开的作用．支架设计的合理性对于治疗过程是至关重要的,如果设计不当导致支架扩张过度或扩张不足,可能会导致血管破裂或起不到扩张血管的作用．因此,支架的变形参数是支架结构设计时需要考虑的重要因素．支架膨胀过程中不同位置的变形程度不一致,端部扩张大于中间部分,这称为不均匀膨胀．另外,支架在膨胀过程中径向的变形会引起轴向的短缩,这称为轴向短缩．如果支架的轴向短缩率较大,将不利于病变处的覆盖,也会危害血管内壁,并且还会使支架定位困难．当气囊被移开,扩张后的支架会发生一定的弹性回复,这称为弹性回弹．支架变形的具体参数如下:

不均匀膨胀率

(1)

式中:Rend和Rmid分别表示支架端部和中部的半径．

轴向短缩率

(2)

式中:Lorig和Lload分别表示支架原始长度和变形后的长度．

弹性回弹率

(3)

式中:Rbefore和Rafter分别表示内压力卸载前和卸载后支架中部的半径．

2 结果与分析

通过对血管支架扩张过程和压力卸载后支架自身回弹过程的有限元计算,确定了3种不同材料的血管支架的膨胀特性．图4～6分别为316L不锈钢、WE43镁合金和PLLA生物可降解聚合物3种血管支架加载前的初始形状和加载后的膨胀结果．对比加载前后的血管支架形状可以看出,3种不同材料的血管支架在径向膨胀的同时都出现了轴向短缩和不均匀膨胀的现象．在支架的撑开状态下,每个支撑单元的两端向两边扩张,但其中的内凹式结构并没有发生明显变形,因此可以保证支撑血管内壁所需要的强度．同时,血管支架沿轴向发生了类似狗骨头状的变形,这是由于血管支架两端没有连接杆而只受单边拉伸所致．

3种不同材料的血管支架模拟结果如表3所示．可以看出,加载后3种支架均膨胀到直径约5 mm时,PLLA支架的不均匀膨胀率为6.00%,明显小于316L不锈钢支架的7.99%和WE43镁合金支架的7.30%．同时,PLLA支架的轴向短缩率11.86%也小于316L不锈钢支架的13.95%和WE43镁合金支架的14.15%．这表明,PLLA支架的均匀膨胀性和轴向短缩性都优于典型的金属材料支架．

图4 316L不锈钢血管支架膨胀模拟结果

图5 WE43镁合金血管支架膨胀模拟结果

图6 PLLA血管支架膨胀模拟结果

表3 血管支架膨胀模拟结果

3种不同材料的支架在膨胀和卸载过程中内压力、不均匀膨胀率和轴向短缩率随支架直径变化的关系曲线如图7～9所示．从图7支架内压力随直径变化的关系曲线可以看出,两种金属材料支架的内压力变化曲线形状相似,而PLLA支架的内压力变化曲线在加载过程中近似呈线性．这说明两种金属材料的支架在膨胀过程中存在一个压力临界值,当内压力较小时直径变化较小,超过临界值后支架迅速膨胀张开；而PLLA支架则在内压力作用下平稳地膨胀张开．3种材料的支架膨胀到相同直径5 mm时,316L不锈钢支架所需的内压力最大,达到了86 kPa,远远超过WE43镁合金支架的38 kPa,而PLLA支架的内压力最小,仅为13.3 kPa．这与材料的弹性模量有关, 316L不锈钢材料的弹性模量分别是WE43镁合金和PLLA材料的4.3倍和45.2倍,如表2所示．因此316L不锈钢支架所需的内压力最高,而PLLA支架具有更好的柔顺性．从图8支架不均匀膨胀率随直径变化的关系曲线可以看出,在加载过程中PLLA支架的不均匀膨胀率始终明显小于另外两种金属材料,而卸载后3种材料的不均匀膨胀率几乎相同,因此PLLA支架对血管内壁的损伤性比另外两种典型金属材料支架要小．图9为支架的轴向短缩率随直径变化的关系曲线,从图中可以看出PLLA支架的轴向短缩率略小于316L不锈钢和WE43镁合金,但差异并不明显．因此可以认为材料种类对轴向短缩率的影响较小,在膨胀过程中对轴向短缩率起着关键作用的是支架结构．

图7 3种支架材料内压力与直径关系曲线

Fig.7 Variation of the internal pressure with respect to the stent diameter for three stent materials

图8 3种支架材料不均匀膨胀率与直径关系曲线

Fig.8 Variation of the uneven expansion rate with respect to the stent diameter for three stent materials

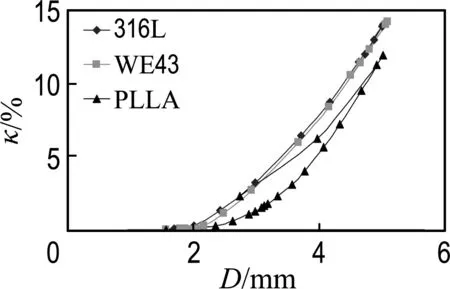
图9 3种支架材料轴向短缩率与直径关系曲线

Fig.9 Variation of the axial shortening rate with respect to the stent diameter for three stent materials

从表3中的卸载后弹性回弹率可以看出,PLLA支架出现了弹性回弹较大的缺陷,回弹率达到了45.42%,显著高于316L不锈钢支架的5.96% 和WE43镁合金支架的11.39%．这是由于PLLA材料的弹性模量和屈服强度远低于这两种金属材料．另外,PLLA支架是否具有足够的径向支撑性能仍有待于进一步的实验验证．为了改善PLLA材料弹性回弹大的缺点,可以通过共聚或共混其他材料等方式进行增强,提高生物可降解材料的弹性模量和屈服强度,将弹性回弹率控制在合理的范围内,获得理想的生物可降解血管支架．通过上述对比分析可以看出,与典型金属材料316L不锈钢和WE43镁合金支架相比,PLLA 血管支架具有更好的轴向柔顺性、均匀膨胀性和轴向短缩性,但是尚存在弹性回弹率较大的缺陷,有待进一步的材料改性研究．

3 结 语

血管支架是经皮穿刺冠状动脉成形术的核心器件,其形状结构和材料特性直接影响着血管支架的使用性能和治疗效果,本文通过对血管支架扩张过程和压力卸载后支架自身回弹过程的有限元分析,研究了PLLA、316L不锈钢和WE43镁合金3种不同材料的血管支架膨胀特性．研究发现,在支架膨胀到相同直径的情况下,PLLA支架所需的内压力明显低于另外两种金属材料的支架,表明PLLA支架具有比典型医用金属材料支架更好的柔顺性．同时PLLA支架的不均匀膨胀率也明显小于另外两种金属材料的支架,表明其具有良好的均匀膨胀性．

通过有限元分析可知,具有内凹式支撑单元的支架不仅表现出合理的相对变形量,还具有良好的均匀膨胀性,可以有效抑制支架在膨胀过程中的不均匀膨胀．但是,PLLA支架的弹性回弹率明显大于316L不锈钢支架和WE43镁合金支架．因此如何提高PLLA材料的弹性模量和屈服强度,保证合理的弹性回弹率,需要进一步深入研究．这些研究结果为血管支架结构的优化设计和支架材料设计提供了有益的帮助．

[1]Tamai H, Igaki K, Kyo E,etal. Initial and 6-month results of biodegradable poly-l-lactic acid coronary stents in humans [J]. Circulation, 2000,102(4):399-404.

[2]Moore J E, Soares J S, Rajagopal K R. Biodegradable stents:biomechanical modeling challenges and opportunities [J]. Cardiovascular Engineering and Technology, 2010,1(1):52-65.

[3]Epstein S E, Speir E, Unger E F,etal. The basis of molecular strategies for treating coronary restenosis after angioplasty [J]. Journal of the American College of Cardiology, 1994,23(6):1278-1288.

[4]Agrawal C M, Haas K F, Leopold D A,etal. Evaluation of poly(L-lactic acid) as a material for intravascular polymeric stents [J]. Biomaterials, 1992,13(3):176-182.

[5]Chua S N D, MacDonald B J, Hashmi M S J. Finite-element simulation of stent expansion [J]. Journal of Materials Processing Technology, 2002,120(1-3):335-340.

[6]Migliavacca F, Petrini L, Colombo M,etal. Mechanical behavior of coronary stents investigated through the finite element method [J]. Journal of Biomechanics, 2002,35(6):803-811.

[7]Pant S, Bressloff N W, Limbert G. Geometry parameterization and multidisciplinary constrained optimization of coronary stents [J]. Biomechanics and Modeling in Mechanobiology, 2012,11(1-2):61-82.

[8]王小平,焦延鹏,崔福斋. 新型可降解金属血管支架的有限元力学分析[J]. 机械设计与研究, 2007,23(5):59-61,69.

WANG Xiao-ping, JIAO Yan-peng, CUI Fu-zhai. Mechanical analysis of new type biodegradable metal stents based on FEM [J]. Machine Design and Research, 2007,23(5):59-61, 69. (in Chinese)

[9]WANG Wei-qiang, LIANG Dong-ke, YANG Da-zhi,etal. Analysis of the transient expansion behavior and design optimization of coronary stents bynite element method [J]. Journal of Biomechanics, 2006,39(1):21-32.

[10]刁繁荣,吕安林,李军杰. 生物可降解性冠状动脉支架的研究进展[J]. 第四军医大学学报, 2006,27(20):1916-1918.

DIAO Fan-rong, LYU An-lin, LI Jun-jie. Progress in researches of biodegradable coronary stents [J]. Journal of the Fourth Military Medical University, 2006,27(20):1916-1918. (in Chinese)

[11]Wu W, Petrini L, Gastaldi D,etal. Finite element shape optimization for biodegradable magnesium alloy stents [J]. Annals of Biomedical Engineering, 2010,38(9):2829-2840.

[12]王伟强. 冠状动脉支架力学行为有限元分析及其结构优化[D]. 大连:大连理工大学, 2005.

WANG Wei-qiang. Finite element analysis of the mechanical behavior of coronary stent and its structure optimization [D]. Dalian:Dalian University of Technology, 2005. (in Chinese)

Finiteelementanalysisofexpansionperformanceofbiodegradablepolymerstents

ZHAODan-yang*,DUNSuo,TIANHui-qing,WANGMin-jie,YUTong-min,LIUYong-yun

( Key Laboratory for Precision & Non-traditional Machining Technology of Ministry of Education, Dalian University of Technology, Dalian 116024, China )

Biodegradable polymer stent is becoming a promising stent, and its expansion performance significantly affects the quality and application of stent. Based on the von Mises yield and isotropic hardening criteria, compared with 316L stainless steel stent and WE43 magnesium alloy stent, the expansion performance of poly L-lactic acid (PLLA) stent was analyzed via the finite element method. It is found that the new PLLA stent has better uniform expansion, foreshortening and flexibility than the other two stents, but the recovery performance needs to be improved.

biodegradable; polymer stents; expansion performance; finite element analysis; isotropic hardening criteria

1000-8608(2014)01-0054-06

2013-04-04；

: 2013-11-28．

“九七三”国家重点基础研究发展计划资助项目(2012CB025905)；国家自然科学基金资助项目(51175060,51275071)；中央高校基本科研业务费专项资金资助项目(DUT12JB10,DUT13ZD105).

赵丹阳*(1976-),男,副教授,博士生导师,E-mail:zhaody@dlut.edu.cn.

R318.01

：A

10.7511/dllgxb201401009