基于OMA试验模态参数的砌体结构有限元建模及修正
管晓明,傅洪贤,王梦恕,崔堃鹏,林凡涛
(北京交通大学 土木建筑工程学院,北京 100044)
在城市地铁建设中较多为下穿隧道工程。用钻爆法开挖隧道时爆破产生的地面振动极易导致临近建筑物损伤甚至破坏。砌体结构房屋建筑因整体性差、应力分布不均匀,更易在隧道施工爆破振动作用下损伤致结构开裂,继而威胁居民的正常工作及生活。因此,该种结构的损伤评价及振动控制技术研究颇受关注,而建立能准确、全面反映砌体真实动力学行为的结构模型为评价结构动力损伤的重要基础。建筑结构模型大多采用有限元模型,但因建模时各种简化及几何、材料、边界等参数取值不确定性,使有限元模型与实际结构有一定差距。目前大多采用模型修正技术建立准确的结构有限元模型。通过对建筑结构进行模态试验获取模态参数(固有频率、振型和阻尼),据结构固有频率参数灵敏度分析选择结构模型中灵敏度较大材料参数修正结构模型,从而使有限元模型分析所得模态参数与试验模态参数趋于一致。该修正方法参数意义明确,结果准确可靠,工程实用性好,已广泛用于机械、桥梁、航天等领域[1-3];但对建筑结构尤其砌体结构模型修正研究较少。
本文以成渝客运专线新红岩隧道工程为背景进行相关研究。该隧道出入口浅埋段下穿重庆市沙坪坝区建设新村与新民坡村,埋深仅15~30 m,隧道周围2、3层砌体房屋密集,且房屋老旧,隧道施工爆破时其安全会直接受到威胁。在隧道上方选一典型2层砖房,通过对砖房进行隧道爆破振动激励的OMA(Operational Modal Analysis)试验获取结构模态参数,采用等效体积单元法建立砌体结构有限元模型,以试验所得模态参数为基准,采用基于结构固有频率的参数灵敏度分析修正方法借助ANSYS软件修正砌体结构有限元模型,为评价砌体结构在隧道施工爆破作用下的动力损伤提供准确、可靠的结构模型。
1 砌体结构有限元模型建立
1.1 砌体结构等效体积单元方法
砌体由砖、砂浆规则砌筑而成,需将砌体均质化为连续性介质,实现采用一种单元建立砌体结构有限元模型。目前大多采用等效体积单元(Representative Volume Element,RVE)法,其包含砌体所有集合与组成信息结构,适用于大规模砌体结构力学行为机理研究。砌体结构等效体积单元建模满足条件[4]为:①包括组成砌体的所有材料,如砖块、砂浆;②能按周期性、连续分布规律组成完整结构;③满足上两条件的最小单元。据此,砌体采用等效体积单元的均质化建模过程见图1。等效体积单元应力应变值用单元中各组成部分的应力应变平均值。等效体积单元用正交各向异性材料模型时的材料参数[4],即将等效体积单元中砖块、砂浆在弹性阶段用各向同性模型,在塑性阶段用Drucker-Prager模型,分别对等效体积单元进行三向(X、Y、Z)单轴抗压及纯剪切试验,获得相应方向弹性模量、泊松比及剪切模量。采用有限元数值分析或室内试验。据试验结果,砌体结构等效体积单元正交各向异性模型参数计算公式[4]为
Ex=σx/εx,μxy=εy/εx,μxz=εz/εx
(1)
Ey=σy/εy,μyx=εx/εy,μyz=εz/εy
(2)
Ez=σz/εz,μzx=εx/εz,μzy=εy/εz
(3)
Gxy=τxy/γxy,Gyz=τyz/γyz,Gzx=τzx/γzx
(4)

图1 砌体等效体积单元均质化过程[5]
对复杂条件下应力状态,砌体采用正交各向异性模型时本构模型为
(5)
式中:εx,εy,εz为正应变;γxy,γyz,γzx为剪应变;σx,σy,σz为正应力;τxy,τyz,τzx为剪应力;Ex,Ey,Ez为弹性模量;μxy,μxz,μyx,μyz,μzx,μzy为泊松比;Gxy,Gyz,Gzx为剪切模量;x,y为水平坐标;z为垂直坐标。
1.2 砌体与混凝土物理力学参数取值
砌体材料参数[6-9]为,密度1 600~2 000 kg/m3,弹性模量1.062~3.646 GPa,泊松比0.15~0.16。据文献[10]烧结普通砖选MU20~MU10,砂浆选M2.5~M5,计算得砌体弹性模量为1.807~3.392 GPa,确定弹性模量为1.800~3.600 GPa,砌体剪切模量按砌体弹性模量的0.4倍选用。混凝土材料参数为,强度等级选C15~C20,弹性模量取22.0~25.5 GPa[11],剪切变形模量可按弹性模量的0.40倍选用,泊松比 0.18~0.22;密度取 2 200~2 400 kg/m3。砌体、混凝土材料参数取值范围及平均值见表1。

表1 砌体、混凝土材料参数取值表
1.3 砌体结构有限元模型建立
经现场调研、实测知,砌体结构有限元模型建模几何参数为,楼层总高7 m,层高3 m,女儿墙高0.7 m,楼板厚0.15 m,外纵墙及承重横墙厚0.24 m,部分隔墙厚0.12 m。房屋一层10.14×7.19 m,二层10.14×8.31 m,挑梁总长3.22 m,二层挑出长度1.12 m。砌体为横向承重结构,二层地面与顶层为混凝土预制板,未设置圈梁及构造柱。二层砖房正、侧面见图2。

图2 二层砖房正面、侧面图
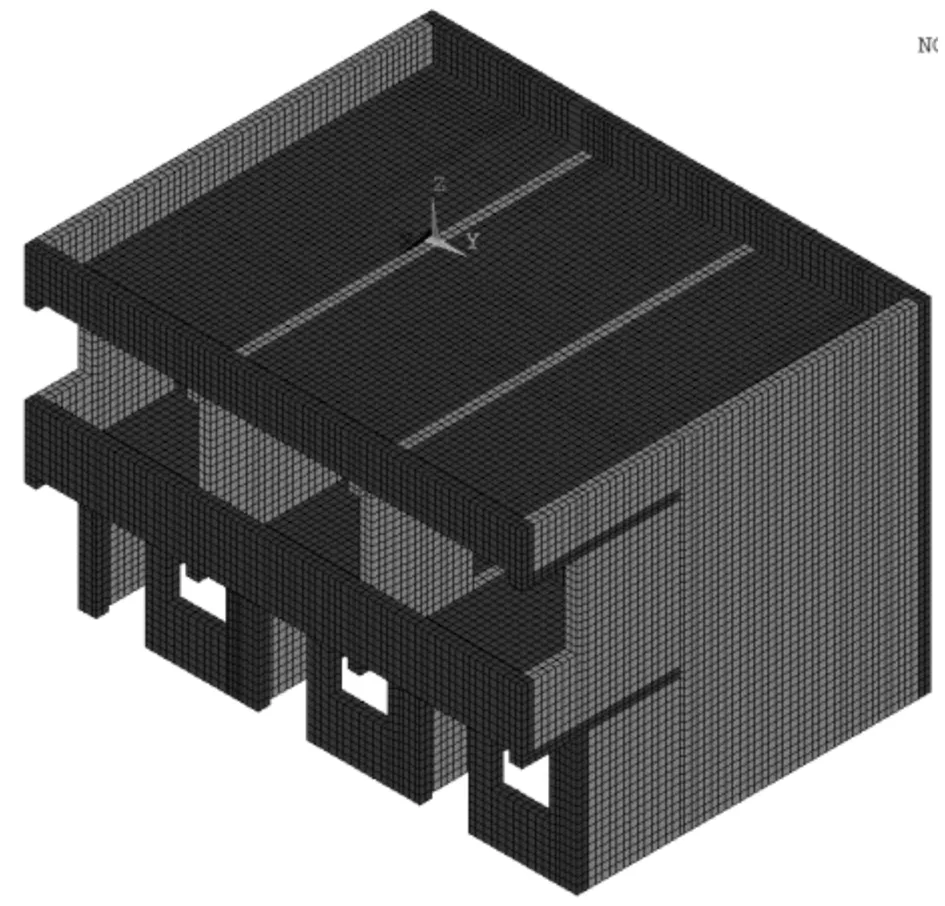
图3 砌体结构初始有限元模型
用ANSYS14.0建立砌体结构有限元模型,建模过程中需适当简化,不考虑楼梯、窗户及门。砌体与混凝土构件均采用solid185六面体单元,砌体结构有限元模型节点66887个,单元40940个,见图3。
2 砌体结构OMA试验与有限元模态分析
2.1 隧道爆破振动激励砌体结构OMA试验
结构模态试验通用方法为试验模态(EMA)法及运行模态(OMA)法。OMA法无需测量激励力,只需测量结构在外界振动激励的响应数据。本文用OMA法进行砌体隧道施工爆破振动激励的模态试验。
OMA模态试验采用同步测试法,布置测点12个,其中一、二楼传感器布置方式一致,纵向测点均4个(Z1,Z2,Z3,Z4),横向测点均2个(H1,H2),见图4。传感器安装时需保持与测量方向一致,底部用石膏固结,需防止振动或人为干扰。试验用TST126型低频水平速度传感器,通过伺服放大器将采集信号传送至数据处理系统进行转换、存储。模态试验选INV3060S型智能数据采集处理分析仪与DASP软件及模态分析软件。试验中测点典型振动波形见图5,测点频谱分析见图6。
隧道爆破振动激励较自然环境振动激励虽持时较短(约1 s,图5),但能量大、频带宽,高频成分丰富(图6),在测点布置足够多条件下,除能激励出结构低阶振型外,亦能激励出结构较高阶振型,此对研究结构在隧道施工爆破作用的动力损伤极为重要。由于爆破地震波主频较高,会致结构发生高阶共振效应,造成局部应力过大,导致结构开裂。故隧道爆破振动激励效果好于自然环境脉动激励;但爆破激励时由于振动能量丰富,易掺杂岩石振动能量或周围房屋振动能量,结构模态参数识别时需谨慎,以确保获取结构固有频率而非周围环境干扰振动频率。

图4 OMA测试传感器一层布置图
2.2 随机子空间法模态参数识别
砌体结构OMA试验后采用随机子空间法(SSI)进行砌体结构模态参数识别。SSI法尤其适用于OMA试验的结构固有频率、阻尼及振型模态参数识别,识别精确度高。SSI法基本模型-离散时间随机状态空间模型[12]为
xk+1=Axk+wk,yk=Cxk+vk
(6)
式中:A为系统离散状态矩阵;C为输出矩阵;xk为离散时间状态向量,yk为输出状态向量;wk,vk为环境激励、测试过程误差,通常设均值为零、互不相关的白噪声协方差矩阵为
(7)
式中:E为数学期望;δpq为Kronrcker delta(p=q时δpq=1,p≠q时δpq=0);p,q,k为离散时间点;Q,S,R为wk及vk协方差矩阵分块矩阵。
随机子空间方法有协方差驱动随机子空间(Cov-SSI)及数据驱动随机子空间(Data-SSI)两种算法。应用较多的数据驱动随机子空间算法识别步骤[13]为
(1) 利用系统输出响应构建Hankel矩阵:
(8)
式中:Y0|2i-1为Hankel矩阵,Y0|2i-1∈R2ij,每行代表块行,即由l个输出响应组成;下标p,f表示“过去”与“将来”,为Hankel矩阵划分块行方式。
(2) 计算“将来”输入行空间在“过去”输入行空间投影,并经QR分解在保持系统原信息情况下缩减数据:
(9)
式中:(·)+为·的广义逆。
通过对Y0|2i-1的Hankel矩阵进行QR分解,Pi可表示为(n为Pi的秩)
Pi=RQT∈Rnij
(10)
投影计算为随机子空间算法核心,可利用“过去”行空间信息预测“将来”;
(3) 对投影进行奇异值分解,并结合卡尔曼滤波理论计算系统状态矩阵A及输出矩阵C;
(4) 对A进行特征值分解,获得特征值、特征向量求解系统模态参数。
采用DASP模态分析软件中SSI方法计算获得稳定图见图7。稳定图含义[14]为,将不同阶数模型模态参数绘于同一幅图中,在相应于某阶模态轴上将高一阶模型识别模态参数与低一阶参数比较,若特征频率、阻尼比及模态振型差异均小于预设的限定值,则该点称稳定点,组成的轴称稳定轴,相应模态即为系统模态。限定值可据实际工程及经验确定,一般设特征频率为1%,阻尼比 5%,模态振型 2%。由图7看出,稳定图由两部分组成,第一部分互谱,在谱峰对应的竖向位置会出现一排特征频率。第二部分用字母“s”“d”“v”“f”“o”分别对应不同阶数计算模型所得特征频率特性。“s”表示频率、阻尼及振型均稳定,“d”表示频率、阻尼比稳定,“v”表示频率、振型稳定,“f”表示频率稳定,“o”表示新频率。若稳定图中谱峰对应的竖向位置出现由低到高的“s”,即对应结构一阶模态。模态参数识别过程中在不明的显谱峰处出现稳定图可能由于计算误差及干扰信号产生的虚假模态引起,需剔除该模态。由图7识别的结构真实模态参数见表2。

图7 SSI法计算的稳定图

表2 砌体结构OMA模态试验分析结果
2.3 有限元模态分析及实测结果对比
为分析砌体采用不同材料模型计算砌体结构模态参数的差别,分别采用各向同性、横观各向同性、正交各向异性材料模型进行模态分析。混凝土用各向同性模型,两种材料物理力学参数取平均值(表1)。砌体材料参数取值为砌体用各向同性模型,选砌体材料参数均值;砌体材料用正交各向异性模型,包含Ex,Ey,Ez,μxy,μyz,μzx,Gxy,Gyz,Gzx9个独立参数。令Ex=Ey=Ez=2.7 GPa,μxy=μyz=μzx=0.15,Gxy=Gyz=Gzx=1.08 GPa。砌体材料采用横观各向同性模型,考虑x,y向同性,包含Ex(或Ey),Ez,μxy,μyz(或μzx),Gyz(或Gzx)5个独立参数。令Ex(Ey)=2.7 GPa,Ez=2.7 GPa,μxy=0.15,μyz(μzx)=0.15,Gyz(Gzx)=1.08 GPa。
模态分析时固定一楼底部节点6个自由度,用Block Lanczos法计算砌体结构1~4阶自振频率及振型,并对比频率计算值与实测值相对误差及总相对误差,总相对误差为前4阶相对误差平方和。初始有限元模型自振频率计算值及实测值相对误差见表3,振型见图8。为分析有限元模型计算振型与试验振型的相关性,采用模态置信准则MAC值(表3)进行验证,MAC值计算公式为
(11)
式中:φai,φei分别为第i阶振型计算及实测振型向量。

表3 砌体不同材料模型下的结构固有频率和MAC值表

图8 砌体结构有限元计算振型
由表3看出:① 无论采用何种材料模型,前4阶自振频率相对误差不一致,第1阶频率相对误差均较小,第2阶频率相对误差均较大,各向同性模型相对误差最大,第3、4阶相对误差为中间值;② 横观各向同性及正交各向异性模型前4阶自振频率值相差不大,且总相对误差小于各向同性模型;③ 不同材料模型的MAC值差别不大,第2阶振型相关性最高,第1、3阶相关程度均大于77%,说明前3阶振型相关性良好,而第4阶实测振型不明显,误差较大,故MAC值较小。
综上分析,砌体采用横观各向同性及正交各向异性模型模态分析结果与实测值更接近,说明各向异性模型能更好反映砌体结构的动力特性,但有限元模型的固有频率与实测值存较大差距,需采用基于结构固有频率的参数灵敏度分析修正。
3 砌体结构有限元模型修正
3.1 结构有限元模型修正方法
砌体结构模型修正为基于OMA模态试验所得模态参数对结构有限元模型材料的物理、力学参数修正。通过对结构有限元模型固有频率参数灵敏度分析,选灵敏度大的材料参数作为修正参数,用ANSYS软件的优化方法进行不断修正,直到有限元计算值与试验值误差最小为止。修正结构模型时先用随机搜索法初步确定最优设计序列,并以此为初始值用零阶或一阶算法进行迭代修正。满足收敛条件时优化迭代结束,所得全局最优设计序列即为材料修正参数的最佳值。
3.2 参数灵敏度分析及修正参数选择
参数灵敏度分析[15]指将结构模态参数表示为模型物理、力学参数的函数。设F(pm)为关于pm=(1,2,…,n)的多元函数,l阶微分灵敏度及差分灵敏度统称为F对pm的l阶灵敏度:
(12)
(13)
式中:F为实测模态参数;pm为材料物理、力学参数,也可为结构几何尺寸。
本文砌体采用三种不同材料模型分别进行结构固有频率的参数灵敏度分析及模型修正,以求获得最优砌体材料模型及参数修正值。砌体各向同性模型参数包括密度(MD)、弹性模量(ME)、泊松比(MP)3个独立参数;砌体横观各向同性模型材料参数包括密度(MD)、弹性模量(MEX、MEZ)、剪切模量(MGXZ)、泊松比(MPXY、MPXZ)6个独立参数;砌体正交各向异性模型材料参数包括密度(MD)、弹性模量(MEX、MEY、MEZ)、剪切模量(MGXY、MGYZ、MGXZ)、泊松比(MPXY、MPYZ、MPXZ)10个独立参数;混凝土用各向同模型材料参数包括密度(CD)、弹性模量(CE)及泊松比(CP)3个独立参数。
本文采用差分灵敏度计算公式,每次计算只改变一个材料参数值,使其增大20%,其它参数不变,计算材料参数对结构前4阶固有频率(FREQ1~FREQ4)灵敏度,以百分比表示。砌体结构固有频率参数灵敏度分析结果见图9~图11。由三图看出,① 砌体密度、混凝土密度及泊松比的增大使结构频率降低,其它参数增大使结构频率增大;②砌体采用各向同性模型时对结构频率影响的参数灵敏度大小依次为ME、MD、CD,其它参数影响较小;横观各向同性模型时对结构频率影响的参数灵敏度大小依次为MD、MGXZ、MEZ、CD、CE、MEX,其它参数影响较小;砌体采用正交各向异性模型时对结构频率影响的参数灵敏度大小依次为MD、MGXZ、 MEZ、CD、CE、MEX、MGYZ,其它参数影响较小。有限元模型修正参数应优先选择灵敏度较大的材料参数。

图9 各向同性模型参数灵敏度分析
3.3 设计变量、状态变量及目标函数
采用ANSYS软件优化设计时需确定设计变量、状态变量及目标函数。设计变量据参数灵敏度分析结果确定:砌体采用各向同性模型时设计变量为ME、MD、CD,砌体采用横观各向同性模型时设计变量为MD、MGXZ、MEX、MEZ、CD、CE,砌体采用正交各向异性模型时设计变量为MD、MGXZ、MGYZ、 MEZ、MEX、CD、CE,设计变量约束条件按表1中材料参数取值范围。状态变量为1~4阶计算频率(FREQ1~FREQ4),分别增大、减小1~4阶实测频率值的10%作为状态变量约束条件,MAC值作为验证计算、实测振型的相关性参考值,满足MACi=1~3≥75%,MAC1i=4≥60%。目标函数用于评价模型修正效果,用前4阶有限元计算频率与实测频率相对误差的平方和作为目标函数,因其修正效率更高、修正效果更明显[16],即
(14)
式中:MBHS为目标函数;fei为试验所得频率;fai为有限元分析所得频率。
3.4 模型修正结果分析
用ANSYS程序优化算法进行模型修正时,优化迭代收敛条件为:当前设计序列与前一设计序列的目标函数值小于目标函数容差ε:
|MBHS(j)-MBHS(j-1)|≤ε
(15)
最佳合理设计序列与当前设计序列目标函数值小于目标函数容差ε:
|MBHS(j)-MBHS(b)|≤ε
(16)
式中:j为迭代次数;ε为较小数:b为最佳设计序列时迭代次数。
砌体结构模型修正后,三种不同模型设计变量及目标函数计算结果及与初始值的差值见表4,计算频率与实测频率相对误差及MAC值见表5。

表4 有限元模型设计变量及目标函数修正结果

表5 模型修正后有限元计算与试验模态参数比较表
由表4、表5看出,① 结构有限元模型修正采用ANSYS优化设计模块多次迭代分析完成,模型修正以目标函数收敛于最小值作为修正目标,故模型修正结果使有限元模型计算所得模态参数总体与实测值趋于一致,不易实现计算与实测每阶模态参数均保持一致或计算值与实测值完全一致。对三种不同材料模型有限元模型修正后目标函数值及计算得结构频率与实测频率相对误差均有减小,且以正交各向异性模型目标函数值为最小。② 有限元模型中需修正的参数通常为难以准确确定的参数,如砌体密度、弹性模量、剪切模量。由修正后材料参数改变量看出,砌体密度、弹性模量及剪切模量改变较大。而在各向异性模型中,正交各向异性模型砌体弹模及剪模的改变量总体小于横观各向同性模型,原因为正交各向异性性模型考虑砌体3个主轴向不同力学参数值,相比横观各向同性模型及各向同性模型而言其修正效果更好。③有限元模型修正后MAC值略有提高,但提高量并不明显,因此模型修正时MAC值验证计算振型与实测振型相关性可起一定参考作用。④ 有限元模型修正后,虽计算频率与实测频率相对误差均有所减小,但部分阶次相对误差仍较大,如第2阶频率,其原因可能为有限元模型未考虑房屋内家具、物品等,测试中存在噪音、干扰信号等,造成有限元模型与实际结构边界条件存在一定误差。
4 结 论
本文通过对砌体结构有限元模型建模及基于OMA模态参数进行结构模型修正研究,结论如下:
(1)采用随机子空间法(SSI)获得二层砌体结构前4阶固有频率位于9~25 Hz。
(2)砌体采用3种材料模型建模时,横观各向同性及正交各向异性模型前4阶固有频率计算值较各向同性模型与实测值更接近,振型相关性更好。
(3)对三种不同材料有限元模型修正后,目标函数值均有减小,计算所得结构频率与实测频率相对误差均有减小,且正交各向异性模型目标函数值最小。MAC值可验证计算振型与实测振型的相关性,有一定参考作用。
(4)有限元模型修正中由于正交各向异性模型考虑砌体3个主轴向不同力学参数值,较横观各向同性模型及各向同性模型修正效果更好。
[1] 夏益霖.基于试验模态参数的结构有限元模型修正[J].振动与冲击,1993,12(1):61-65.
XIA Yi-lin.Finite element structural model updating based on experiment modal parameters[J].Journal of Vibration and Shock, 1993, 12(1): 61-65.
[2] 韩芳,钟冬望,汪君.基于贝叶斯法的复杂有限元模型修正研究[J].振动与冲击,2012,31(1):39-43.
HAN Fang,ZHONG Dong-wang,WANG Jun.Complicated finite element model updating based on Bayesian method[J].Journal of Vibration and Shock, 2012, 31(1): 39-43.
[3] 殷海涛,姜金辉,张方,等.基于试验模态参数及结构动力学优化设计的有限元建模[J].国外电子测量技术,2012,31(9):18-22.
YIN Hai-tao, JIANG Jin-hui, ZhANG Fang, et al.Finite element modeling based on experimental modal parameters and structural dynamics optimization[J].Foreign Electronic Measurement Technology, 2012, 31(9):18-22.
[4] Wu Cheng-qing, Hao Hong.Derivation of 3D masonry properties using numerical homogenization technique[J].International Journal For Numerical Methods In Engineering, 2006, 66(11): 1717-1737.
[5] Wei Xue-ying, Hao Hong.Numerical derivation of homogenized dynamic masonry material properties with strain rate effects[J].International Journal of Impact Engineering, 2009, 36(3): 522-536.
[6] 仲继寿,杨舜臣,肖跃军.矿山采动区砖砌体房屋三维有限元模型的建立与分析[J].中国矿业大学学报,1993,22(2):40-47.
ZHONG Ji-shou, YANG Shun-chen, XIAO Yue-jun.The establishment of a three dimensional finite element model of brick masonry buildings subjected to mining ground deformation[J].Journal of China University of Mining & Technology, 1993, 22(2): 40-47.
[7] 魏海霞,陈士海,张安康.基于动力有限元方法的典型砌体结构爆破振动安全标准的探讨[J].振动与冲击,2011,30(5):49-53.
WEI Hai-xia, CHEN Shi-hai, ZHANG An-kang.Safety standards discussion for blasting vibration of typical masonry buildings with dynamic finite element method[J].Journal of Vibration and Shock, 2011, 30(5): 49-53.
[8] 刘富君,朱玉华,马晓辉.内构造柱加固砌体墙抗震性能有限元分析[J].结构工程师,2011,27(3):62-66.
LIU Fu-jun, ZHU Yu-hua, MA Xiao-hui.Finite element analysis for seismic performances of unreinforced masonry walls strengthened with inside structural column[J].Structural Engineers, 2011, 27(3): 62-66.
[9] 谭晓晶,吴斌,辛文杰.林甸县农村砌体房屋抗震性能调查与分析[J].建筑科学与工程学报,2012,29(2):36-42.
TAN Xiao-jing, WU Bin, XIN Wen-jie.Investigation and analysis of seismic behavior of masonry buildings in rural areas located in Lindian country[J].Journal of Architecture and Civil Engineering, 2012, 29(2): 36-42.
[10] GB 50003-2001,砌体结构设计规范[S].
[11] GB 50010-2010,混凝土结构设计规范[S].
[12] 肖祥,任伟新.实时工作模态参数数据驱动随机子空间识别[J].振动与冲击,2009,28(8):148-153.
XIAO Xiang, REN Wei-xin.Improved data-driven stochastic subspace identification of online operational modal parameters[J].Journal of Vibration and Shock, 2009, 28(8): 148-153.
[13] Van O P, Moor D B.Subspace identification for linear systems: theory implementation applications[M].Dordrecht: The Netherlands: Kluwer Academic Publishers, 1996.
[14] 禹丹江.土木工程结构模态参数识别-理论、实现与应用[D].福州:福州大学,2006.
[15] 沃德·海伦,斯蒂芬·拉门兹,波尔·萨斯,著.白化同,郭继忠,译.模态分析理论与试验[M].北京:北京理工大学出版社,2001.
[16] 卞广为.大跨斜拉桥有限元模型修正的数值模拟与试验研究[D].哈尔滨:哈尔滨工业大学,2008.

