一种七自由度冗余机械臂的奇异构形特征分析

， ，

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001)

一种七自由度冗余机械臂的奇异构形特征分析

史士财，尹斌，蒋再男

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001)

总结了对七自由度冗余机械臂进行奇异性分析的常用方法，并引入了一种基于相关旋量抑制的方法。采用这种方法，对一种构型与加拿大臂2相同的七自由度冗余机械臂进行了奇异性分析，得出了七自由度冗余机械臂出现奇异时的5种情况。为了深入和形象地理解机械臂的奇异构形，针对每种情况进行了详细分析，得出了每种情况对应的奇异构形的几何特征，并用图解形式直观地给出了奇异构形的例子。

七自由度冗余机械臂；奇异性分析；相关旋量抑制方法；奇异构形特征

0 引言

七自由度机械臂是能够完成多维空间任务的冗余机械臂中结构最为简单的，同时也具有了操作灵活、避障、避奇异和力矩优化等优点，因而得到学术界的关注，并得到广泛应用。加拿大臂2(Canadarm2)[1]和SPDM(special purpose dexterous manipulator)[2]都采用了七自由度的构形，并在国际空间站的建设和维护中做出重要贡献。七自由度冗余机械臂的奇异性分析，为机器人机构设计和控制器算法设计提供了理论基础[3-7]。在此，采用了参考文献[5]中提出的相关旋量抑制的方法，分析了一种七自由度冗余机械臂的奇异性。

1 相关旋量抑制的方法

相关旋量抑制的方法是一种针对七自由度冗余机械臂失去1个自由度的奇异性分析方法，这种方法简化了奇异性分析的复杂运算过程。对一个七自由度冗余机械臂，它的旋量矩阵可以表示为[$]=[$1$2$3$4$5$6$7]，$i为第i关节的旋量。当机械臂处于奇异构形时，这个6×7的旋量矩阵将欠秩。为了方便叙述，称这7个关节旋量中任意6个的集合为基旋量，对应的旋量矩阵称为基子矩阵。采用该方法，对七自由度机械臂进行奇异性分析，需要经过以下2步。

a.找出基子矩阵不满秩的条件。当基子矩阵不满秩时，满足以下等式：

(1)

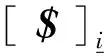
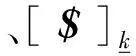
(2)

联立式(1)、式(2)，可以得到七自由度冗余机械臂出现奇异构形的条件。

2 一种七自由度机械臂的奇异性分析

2.1 七自由度机械臂的运动学模型

本次的研究对象是一个七自由度机械臂，采用R⊥R⊥R∥R∥R⊥R⊥R的自由度配置，R代表旋转关节，⊥代表2个关节的轴线相互垂直，∥代表2个关节的轴线相互平行，与Canadarm2构型[8]相同，但结构参数不一样。该机械臂的D-H参数如表1所示。

表1 七自由度机械臂D-H参数

序号θi/(°)di/mmai-1/mmαi-1/(°)10a000290a109030a20-9040a4a3050a6a506-90a7090790a80-90

由于关节1的旋量表达式较为复杂，故选择关节2～关节7的关节旋量作为基旋量。同时，为简化关节旋量的计算[9]，选择关节5的坐标系F5-x5y5z5为参考坐标系计算各个关节的旋量。该七自由度冗余机械臂的关节旋量矩阵为：

5[$]=[5$15$25$35$45$55$65$7]

基子矩阵为：

(3)

2.2 基子矩阵欠秩的条件

s4s6(a3c3+a3c34+a6s345)=0

(4)

要使式(4)成立，需满足以下情况。

第1种情况：

s4=0

(5)

第2种情况：

s6=0

(6)

第3种情况：

a3c3+a3c34+a6s345=0

(7)

2.3 旋量矩阵欠秩的额外条件

基子矩阵不满秩的条件有3种情况，如式(5)～式(7)。在此，将针对每种情况，先找出相关旋量，然后计算抑制矩阵不满秩的条件，从而得出旋量矩阵欠秩的额外条件。

2.3.1 第1种情况

(8)

2.3.2 第2种情况

推导方法与第1种情况相同，在此不再赘述，直接给出结果。这种情况下七自由度冗余机械臂出现奇异分别有2种情况：

(9)

(10)

2.3.3 第3种情况

推导方法与第1种情况相同，在此不再赘述，直接给出结果。这种情况下七自由度冗余机械臂出现奇异分别有2种情况：

(11)

(12)

机械臂的关节角度关系只要在满足5个方程式组中的任意1个，就会出现失去1个自由度的奇异构形。

3 七自由度机械臂奇异构形的特征分析及图解

为了对七自由度机械臂的奇异构形有一个形象的理解，分析了机械臂出现奇异时所具有的构形特征，对每种情况给出例子，用图解的形式来表示。

3.1 第1种情况

这种情况对应式(8)。s4=0，即关节4的角度为0°或±180°，又关节3，4，5的轴线相互平行，故关节3，4，5的轴线共面。

第2个式子由于过于复杂，没有分析出它对应的几何意义。但此时可以看作是关节4固定，即等价为一个构型为R⊥R⊥R∥R⊥R⊥R的六自由度机械臂，失去1个自由度时的奇异构形。这里给出这种情况下的特例，各个关节的角度为[0° 0° 0° 0° 0° 0° 0°]，即机械臂处于零位姿时，机械臂的构形如图1所示；各个关节角度为[0° 0° 0° 180° 0° 0° 0°]时，机械臂的构形如图2所示。

语文组“深入”探讨此次研学活动后，对以下四方面进行了整合思考：（1）跨学科主题与学科内主题的整合（天坛的传统文化）；（2）研究课程的“纵深”关系（研究话题的整合，任务直指核心能力）；（3）研学活动的传统文化价值；（4）“后研学”活动的开展。

图1 第1种奇异构形的例子1

图2 第1种奇异构形的例子2

3.2 第2种情况

这种情况对应式(9)。此时，关节2角度为0°或±180°，意味着关节1的轴线与关节3的轴线平行；关节6角度为0°或±180°，意味着关节7的轴线与关节5的轴线平行。又因为关节3，4，5的轴线相互平行，因此，这种情况下机械臂的奇异构形特征是：关节1，3，4，5，7的轴线相互平行。

这里给出这种情况下的例子，取各个关节的角度为[0° 0° 20° 50° -30° 180° 70°]，机械臂的构形如图3所示。

图3 第2种奇异构形的例子

3.3 第3种情况

这种情况对应式(10)。

a.分析1。关节6角度为0°或±180°，则关节7的轴线与关节5的轴线平行，6号坐标系的y-z平面与关节7的轴线、关节5的轴线形成的平面共面。

b.分析2。1号坐标系到6号坐标系的齐次变换矩阵的(1，4)元素，即x分量为c6(-a3c5-a3c45+a1s345)，显然，此时x分量为0，即1号坐标系的原点位于6号坐标系的y-z平面上。

图4 第3种奇异构形的特例

综上可知，这种情况下机械臂的奇异构形特征为：关节7的轴线与关节5的轴线平行，且1号坐标系原点位于关节7的轴线、关节5的轴线所形成的y-z平面上。

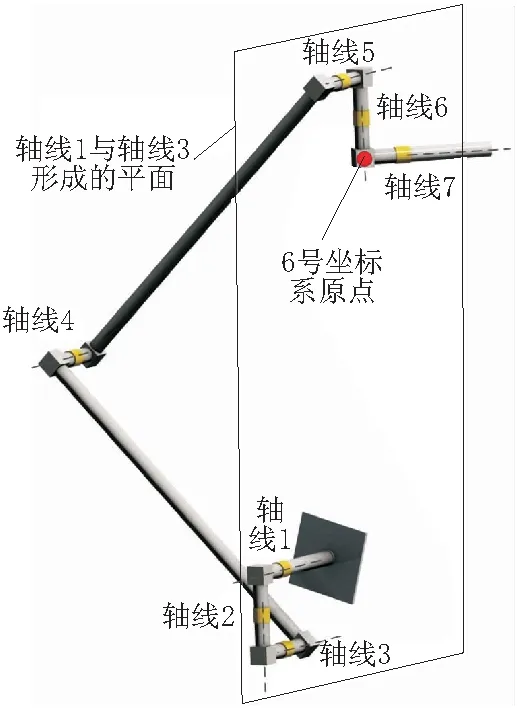
图5 第4种奇异构形的例子

3.4 第4种情况

这种情况对应式(11)。

a.分析1。s2=0，则关节1的轴线与关节3的轴线平行，2号坐标系的y-z平面与关节1的轴线和关节3轴线形成的平面共面。

b.分析2。6号坐标系到2号坐标系的齐次变换矩阵的(1，4)元素，即x分量为a3c3+a3c34+a6s345，显然，x分量为0，即6号坐标系的原点位于2号坐标系的y-z平面。

综上可知，这种情况下机械臂的奇异构形特征是：关节1的轴线平行于关节3的轴线，且6号坐标系原点位于关节1的轴线和关节3的轴线所形成的平面上。

这里给出这种情况下的一个特例，各个关节的角度为[15° 180° 45° 90° -135° 45° 30°]，机械臂的构形如图5所示。

3.5 第5种情况

这种情况对应式(12)。

a.分析1。6号坐标系到2号坐标系的齐次变换矩阵的(1，4)元素，即x分量为a3c3+a3c34+a6s345，显然，x分量为0，即6号坐标系的原点位于2号坐标系的y-z平面。

b.分析2。6号坐标系到1号坐标系的齐次坐标变换矩阵的(2，4)元素，即y分量为-a1+a3s3+a3s34-a6c345，显然，y分量为0，即6号坐标系的原点位于1号坐标系的x-z平面。

综上可知，这种情况下的奇异构形特征是：6号坐标系的原点位于一条线上，这条线是由1号坐标系的x-z平面和2号坐标系的y-z平面相交形成的。

这里给出这种情况下的一个特例，各个关节的角度为[0° 0° 80.319° 175° -99.681° 45° 0°]，机械臂的构形如图6所示。

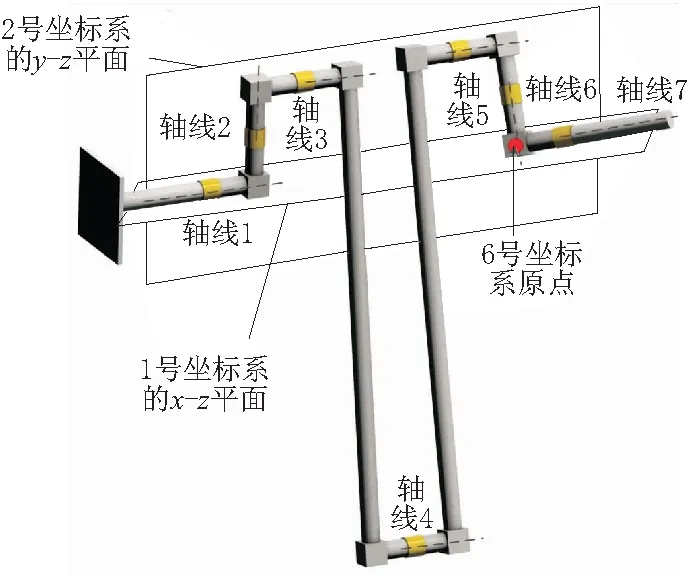
图6 第5种奇异构形的例子

4 结束语

采用相关旋量抑制的方法，对一种构型与Canadarm2相同的七自由度机械臂进行了奇异性分析，得出了机械臂出现奇异的5种条件。为使对七自由度冗余机械臂奇异构形的理解不局限在公式层面，详细分析了每种条件，给出了每种条件对应的奇异构形特征，并用图解形式直观地给出了奇异构形的例子。所用的分析方法和结论,适用于与本文机械臂构型相同的任何七自由度冗余机械臂。

[1] 张凯锋，周 晖，温庆平，等.空间站机械臂研究[J].空间科学学报，2010，30(6)：612-619.

[2] Coleshill E，Oshinowo L，Rembala R，et al. Dextre: improving maintenance operations on the international space station[J]. Acta Astronautica，2009，64(9):869-874.

[3] 丑武胜，吴 忠，王田苗，等.冗余机械臂运动奇异性分析[J].机械工程学报，2000，36(9)：33-36.

[4] Nokleby S B. Singularity analysis of the Canadarm2[J]. Mechanism and Machine Theory，2007，42(4):442-454.

[5] Kong X，Gosselin C M. A dependent-screw suppression approach to the singularity analysis of a 7-DOF redundant manipulator:Canadarm2[J]. Transactions of the Canadian Society for Mechanical Engineering，2005，29(4):593-604.

[6] Boudreau R，Podhorodeski R P. Singularity analysis of a kinematically simple class of 7-jointed revolute manipulators[J]. Transactions of the Canadian Society for Mechanical Engineering，2010，34(1):105-117.

[7] Xu W F，Zhang J T，Qian H H，et al. Identifying the singularity conditions of canadarm2based on elementary Jacobian transformation[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems，Tokyo，Japan，2013:795-800.

[8] Gibbs G，Sachdev S. Canada and the international space station program: overview and status[J].Acta Astronautica，2002，51(1):591-600.

[9] Waldron K J，Wang S L，Bolin S J.A study of the Jacobian matrix of serial manipulators[J].Journal of Mechanisms，Transmissions and Automation in Design，1985，107(2):230-238.

Features Analysis of Singular Configurations of a 7-DOF Redundant Manipulator

SHIShicai，YINBin，JIANGZainan

(State Key Laboratory of Robotics and System，Harbin Institute of Technology，Harbin 150001，China)

Popular methods for singular analysis of a 7degrees of freedom (DOF) redundant manipulator are summarized. A depend-screw suppression approach is introduced and applied to the singular analysis of a 7-DOF redundant manipulator，whose configuration is identical with Canadarm2. Five sets of conditions defining singular configurations are obtained. In order to have a deep and visual understanding of singular configurations，each condition is analyzed in detail. Geometric features and illustration of singular configurations of the 7-DOF manipulator are presented.

7-DOF redundant manipulator; singularity analysis; dependent-screw suppression approach; feature of singular configurations

2014-06-05

国家自然科学基金资助项目(51305097)；教育部博士点基金资助项目(20122302120046)

TP24

A

1001-2257(2014)10-0067-04

史士财(1978-)，男，辽宁辽中人，博士，副研究员，研究方向为机器人技术；尹斌(1989-)，男，河南新郑人，硕士，研究方向为机器人技术；蒋再男(1982-)，男，安徽岳西人，博士，助理研究员，研究方向为空间机器人遥操作、人机交互技术。