基于小波包分解的滚动轴承故障信号频域特征提取方法研究

，

(昆明理工大学机电工程学院，云南 昆明 650500)

基于小波包分解的滚动轴承故障信号频域特征提取方法研究

丘世因，袁锐波

(昆明理工大学机电工程学院，云南 昆明 650500)

0 引言

机械故障诊断的本质就是模式识别的应用过程[1]。据统计，30%的旋转机械故障由轴承故障引起，90%的滚动轴承故障来自内圈和外圈的故障[2]。利用轴承运行过程中产生的振动信号进行故障诊断是常用的方法。当滚动轴承发生故障时，轴承的部件在运行过程中会周期性的撞击故障部位，产生一系列的冲击振动，这些冲击振动的出现使所测得的信号呈现出非平稳振动信号特征[3]，由于小波分析对非平稳瞬态信号的处理具有宽频响应的特点，故目前对轴承振动信号的分析多采用小波分析的方法,国内外众多学者对此进行了大量的研究，田野等[2]利用小波包分解提取不同频段内的振动能量，并采用支持向量机进行轴承故障的模式识别；Teotrakool K等人[4]介绍了小波包分解法在转速变化的轴承故障诊断中的应用，实验证明采用小波包分解法能够较早地发现故障特征; Eren L等人[5]的研究表明通过小波包分解能够找到覆盖轴承故障特征的频段；杨国安等人[6]研究了基于小波包分解的时域特征提取方法，分别重构不同频带内的分解系数，从重构的时间序列中进行特征提取，将方差和峭度作为故障诊断参数，该方法不仅能够识别故障，而且还能找出某个特定频带下的信号特征。

在前人研究的基础上，提出一种基于小波包分解的频域特征提取方法，利用小波包对轴承振动信号进行三层分解，重构第三层的所有节点，提取重构信号频谱的峰值作为故障特征空间的故障特征点。由于轴承故障发生部位和轴承结构的不同, 轴承振动信号的能量在频域的分布也不同[2]，为了提取轴承故障的特征，需要找到最优的小波包节点，使其重构信号中包含最明显的轴承故障特征，为此需要计算特征空间中特征点与特征点中心之间的平均欧氏距离，若某个小波包节点为最优节点，则由其重构信号构建的特征空间的平均欧氏距离是最小的，因为此时故障信号的能量集中在该节点代表的频带内，接着重构最优小波包节点得到最优重构信号，从最优重构信号的频谱中提取峰值作为特征点，重复上述过程，直到4种轴承状态的特征点全部提取出并构成轴承状态特征空间，最后使用K均值聚类法对特征空间中的特征点进行聚类。

1 小波包变换及算法

小波包变换是在多分辨率分析基础上构成的一种更精细的正交分解方法, 它在全频带对信号进行多层次的频带划分。它继承了小波变换良好的时频局部化特点，又继续对小波变换没有再分解的高频频带做进一步的分解， 从而提高了频率分辨率，小波包分析同时在低频和高频部分进行分解，自适应地确定信号在不同频段的分辨率。

小波包分解和重构算法为:

(1)

小波包算法分解到第N层时，将得到2N个子频带。N=3时的小波包分解树如图1所示，第3层一共有8个节点。

图1 小波包分解树

小波包变换的信号分解是将包括正弦信号在内的任意信号划归到相应的频带里，因而这些分解频带信号都具有一定的能量，由于不同的轴承故障能量分布在不同的频段内[2]，即不同轴承故障的能量包含在不同节点的重构信号中[3]，故必须找到包含故障特征能量的最优小波包节点。

2 平均欧氏距离

平均欧式距离是系统聚类法中使用最普遍的一个距离指标[7]，可用来衡量类内离散度，利用最小平均欧氏距离作为衡量故障能量在某频段内的集中程度，找到了故障能量最为集中的频段也就找到了最优小波包节点。第i类样本xik和全体样本的均值μi间的平均欧氏距离为:

(2)

n为第i类的样本总数。

3 试验分析

3.1 试验准备

采用美国Case Western Reserve University电气工程实验室的滚动轴承试验数据[8]来验证所提方法的有效性。试验分析选用电机驱动端的轴承振动数据，采用加速度传感器测量振动信号，采样频率为12 kHz，试验的轴承采用6205-2RS JEM SKF深沟球轴承，轴承节径为39.04 mm，滚动体共9个，滚动体直径为7.94 mm。试验选用了转速在1730r/min、1750r/min、1772 r/min和1797 r/min下的轴承内圈、外圈、滚动体故障数据以及无故障轴承的数据，共包含800份数据。其中，每种转速包含200份数据(每种轴承状态包含50份数据,每份数据持续时间为0.1s)。详细介绍转速为1750r/min时，4种轴承状态的特征提取与模式识别方法，其余3种转速下的轴承状态识别方法与之相同。

3.2 轴承状态特征提取

转速为1750r/min的振动数据，包含4种轴承状态(内圈、外圈、滚动体故障以及无故障状态，共200份数据)，每种轴承状态包含50份数据，将这50份数据分为训练集(20份)以及测试集(30份)两部分，对训练集中每种状态的每一份数据进行小波包分解(分解3层)，第3层得到8个小波包节点，再重构这8个节点的信号，从8个重构信号的频谱中提取峰值作为特征点，得到8个特征点，于是每种状态将能得到一个20×8的特征空间(160个特征点)，特征空间的第1列代表从小波包节点[3,0]的重构信号中提取的特征点，其余以此类推。

由于篇幅所限，仅展示1750r/min转速下节点[3,1]和节点[3,4]的训练集重构信号特征空间，如图2所示，图2中“+”号代表内圈故障特征点；“*”代表外圈故障特征点；“▽”代表滚动体故障特征点；“○”代表无故障特征点；“×”代表轴承状态特征点中心(平均值点)，从图2a的特征点分布规律可以发现，节点[3,1]的特征空间中4类轴承状态的特征点分布较为稀疏，并且外圈故障、滚动体故障和无故障3类的特征点中心之间的距离较短，产生了一定的混叠；节点[3,4]的特征空间中滚动体故障和无故障的特征点分布较为紧密，内圈和外圈的特征点分布较为稀疏。从试验中发现，节点重构信号的特征点分布疏密程度与小波包节点的选取有关，说明不同故障的特征位于不同的频段内。为了准确提取故障特征，需要找到最优的小波包节点，使该节点的重构信号中包含最明显的故障特征，这样可以使特征点的分布变得紧密，有利于提高轴承故障模式识别的准确率。

图2 重构信号特征空间(1750r/min)

如果从某个节点的重构信号中提取的特征点最密集，说明该节点的重构信号包含了最明显的轴承故障特征，则该节点为最优的小波包节点，采用平均欧氏距离作为衡量特征点集中程度的标准。首先对训练集的20份内圈故障信号进行3层小波包分解，并重构所有小波包节点的信号，提取重构信号频谱的峰值作为特征点，得到20×8的特征空间(160个特征点)，然后分别计算8个节点对应的内圈故障特征空间(每个节点对应的特征空间包含20个特征点)中每个特征点到特征空间中心的平均欧氏距离，最小平均欧氏距离所对应的节点即为最优小波包节点，转速为1750r/min时，特征点到特征空间中心的平均欧氏距离如表1所示。重复上述方法可以得到外圈故障、滚动体故障以及无故障特征空间的平均欧氏距离，见表1。

从表1的数据中可以看到，在1750r/min转速下的内圈故障特征点平均欧氏距离在节点[3,0]处最小，说明节点[3,0]的重构信号包含了内圈故障特征。因此，内圈故障的最优小波包节点为[3,0]，以此类推可以得到1750r/min转速下，其余轴承状态对应的最优小波包节点，如表2的第2行所示。重复上述的过程，可以得到其余3种转速下的最优小波包节点，如表2所示。找到并重构最优小波包节点后，便可以从最优重构信号中提取故障的特征。

表1 平均欧氏距离(1750r/min)

对1750r/min转速下的4种轴承状态的最优小波包节点进行重构，然后提取重构信号的特征点，构成训练集最优特征空间，如图3所示，再利用K均值聚类方法对训练集最优特征空间进行聚类。重复上述方法对其余3种转速下的轴承状态进行特征提取和K均值聚类。

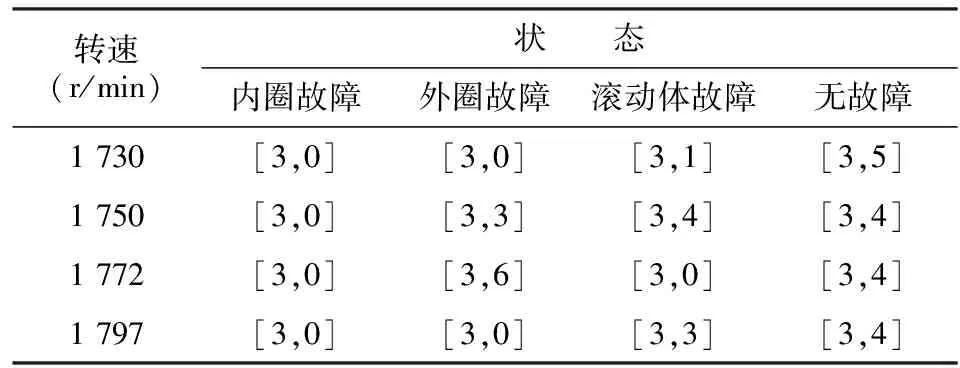
表2 最优小波包节点

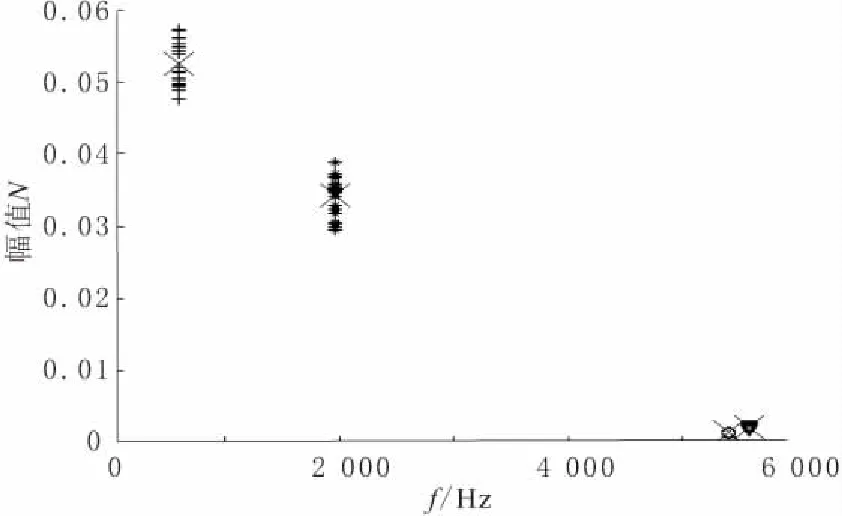
图3 训练集最优特征空间(1750r/min)

从图3中可以看到，训练集最优特征空间中的特征点明显地分布在了4个区域，分别代表轴承的4种状态(内圈故障、外圈故障、滚动体故障和无故障)，4个区域之间的距离较远且每个区域内的特征点分布较为紧密。图中的“×”代表聚类中心，经过K均值聚类算法后找到了4个聚类中心，并将特征空间(80个特征点)划分为了4类，1750r/min转速下的聚类结果如表3所示，内圈故障的特征点数为20个且全部归为类别1，说明转速为1750r/min时，轴承内圈故障特征点的正确聚类率为100%。同理，外圈故障、滚动体故障及无故障特征点的正确聚类率均为100%。其余3种转速下4种轴承状态的正确聚类率也均为100%，有利于提高测试集轴承状态模式识别的准确率。

表3 训练集K均值聚类结果(1750r/min)

3.3 轴承状态模式识别

前面已经利用平均欧氏距离法找到了训练集轴承数据的最优小波包节点以及训练集最优特征空间，接下来按前面所提方法对测试集轴承数据(共120份数据，4种轴承状态各占30份数据)进行3层小波包分解,重构最优小波包节点的信号并提取状态特征，构成测试集最优特征空间，再将其与训练集最优特征空间进行合并，构成最优模式识别特征空间，最后对最优模式识别特征空间进行K均值聚类，从而实现对测试集轴承数据的模式识别，1730r/min和1750r/min转速下的测试集K均值聚类结果分别如图4、图5所示。“□”代表测试集特征点，从这2幅图中可以看到，测试集的4种轴承状态特征点同样明显地分布在了4个区域，并且这4个区域与训练集的特征区域基本重合。故通过对最优模式识别特征空间进行聚类，便可以知道测试集数据所属的轴承状态。

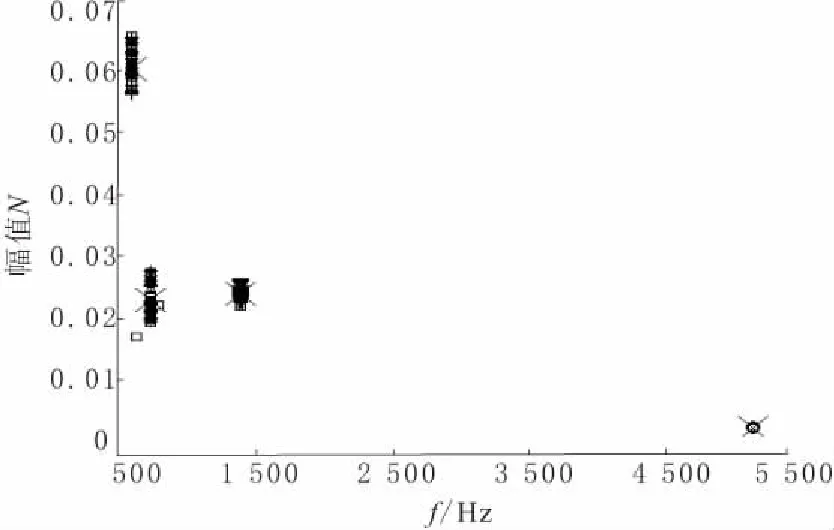
图4 最优模式识别特征空间(1730r/min)

图5 最优模式识别特征空间(1750r/min)

表4为转速为1730r/min时测试集轴承状态的模式识别结果，其中，外圈故障有一个特征点被误识别为内圈故障，模式识别率为96.67%，其余3种轴承状态的模式识别率均为100%。

表5、表6、表7分别为转速1750r/min、1772 r/min和1797 r/min时的轴承状态模式识别结果，4种轴承状态的模式识别率均为100%。从试验数据中发现，除了转速为1730r/min时外圈故障的识别率为96.67%外，其余转速下的轴承状态识别率均达到100%，证明了所提方法的有效性。

表4 测试集K均值聚类结果(1730r/min)

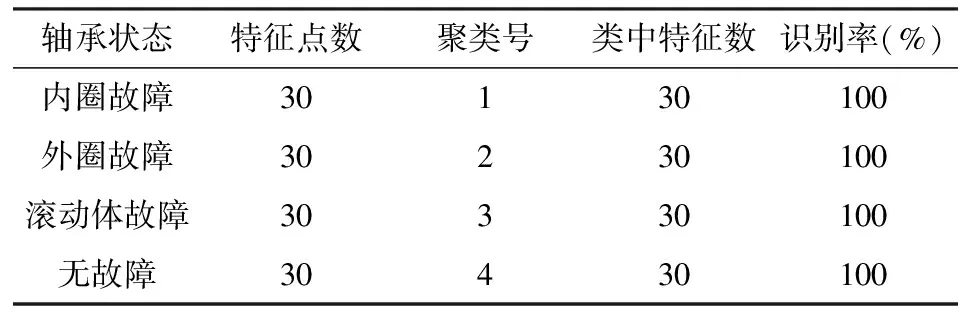
表5 测试集K均值聚类结果(1750r/min)

表6 测试集K均值聚类结果(1772 r/min)

表7 测试集K均值聚类结果(1797 r/min)

4 结束语

研究结果表明，一方面，对于不同的轴承状态其状态特征位于不同的频段内，利用小波包分解法可以找到包含最明显的状态特征的频段，另一方面，试验证明利用平均欧氏距离能够找到最优的小波包节点，重构最优小波包节点可以得到最优重构信号，从最优重构信号的频谱中提取峰值作为特征空间的特征点，此时的特征空间具有最低的类内离散度，说明最优重构信号能够包含最明显的轴承状态特征。从试验结果中看到，该方法能够适应不同转速下的轴承状态识别，可以获得较高的轴承状态模式识别准确率，为滚动轴承故障的特征提取提供了一种新的思路。

[1] 许国根,贾 瑛.模式识别与智能计算的Matlab实现[M].北京:北京航空航天大学出版社,2012.

[2] 田 野,陆 爽.基于小波包和支持向量机的滚动轴承故障模式识别[J].机床与液压,2006,(6):236-246.

[3] Sun Fang,Wei Zijie. Rolling bearing fault diagnosis based on wavelet packet and RBF neural network[A].Proceedings of the 26th Chinese Control Conference[C].2007.451-455.

[4] Teotrakool K,Devaney M J,Eren L.Adjustable-speed drive bearing-fault detection via wavelet packet decomposition[J].IEEE Transactions on Instrumentation and Measurement,2009,58(8):2747-2754.

[5] Eren L, Devaney M J.Bearing damage detection via wavelet packet decomposition of the stator current[J].IEEE Transactions on Instrumentation and Measurement,2004,53(2):431-436.

[6] 杨国安,钟秉林,黄 仁,等.机械故障信号小波包分解的时域特征提取方法研究[J].振动与冲击,2001,20(2):25-28.

[7] 张大克,王玉杰.随机平均欧氏距离的统计性质与分类阈值[J].天津科技大学学报,2008,23(4):85-88.

[8] Case western reserve university bearing data center website. Bearing test data[EB/OL].http://www.eecs.cwru.edu/laboratory/bearing,2011-4.

Research of the Rolling Element Bearing Fault Signal Frequency Domain Feature Extraction Method Based on the Wavelet Packet Decomposition

QIUShi-yin,YUANRui-bo

(Faculty of Mechanical and Electrical Engineering,Kunming University of Science and Technology,Kunming 650500,China)

对轴承故障信号进行3层小波包分解，重构第3层所有节点，提取重构信号频谱的峰值作为故障特征点并构成特征空间，计算特征空间的平均欧氏距离，平均欧氏距离最小时对应的节点即为最优小波包节点，重构最优节点得到最优重构信号并从中提取特征点构成最优特征空间，最后，对最优特征空间进行K均值聚类。对4种转速下轴承的4种状态进行特征提取与模式识别试验，结果表明，运用该方法能有效提取轴承故障的特征，并使故障特征空间具有最低的类内离散度，获得了较高的模式识别准确率。

轴承故障；特征提取；小波包分解；最优节点；K均值聚类；模式识别

First of all,the bearing fault signals were decomposed into three layers wavelet coefficients by which the bearing fault signals were reconstructed.The peak values extracted from the reconstructing signal spectrum constructed a feature space.Then,the minimum average Euclidean distance calculated from the feature space indicated the optimal wavelet packet node.The optimal feature space could be constructed by the feature points extracted from the signals reconstructed by the optimal wavelet packet nodes.Finally,the optimal feature space was used for the K-means clustering.The feature extraction and pattern recognition test of the four kinds of bearing conditions under four kinds of rotation speeds was detailed.The test results show this method, which can extract the bearing fault feature efficiently and make the fault feature space have the lowest within-class scatter,wons a high pattern recognition accuracy.

bearing fault;feature extraction;wavelet packet decomposition;optimal node;K-means clustering;pattern recognition

2013-11-06

云南省自然科学基金重点项目(2010CD030)

TH133；TP391

A

1001-2257(2014)05-0012-05

丘世因(1990-),男,云南昆明人,硕士研究生,研究方向为流体传动控制；袁锐波(1968-),男,云南昆明人,博士,教授，研究方向为电液比例伺服控制、气动伺服控制。