二水平设计离散偏差和对称化L2偏差紧的下界*
李洪毅,黎奇升,欧祖军
(1.吉首大学师范学院,湖南 吉首 416000;2.吉首大学数学与统计学院,湖南 吉首 416000)
二水平设计离散偏差和对称化L2偏差紧的下界*
李洪毅1,2,黎奇升2,欧祖军2
(1.吉首大学师范学院,湖南 吉首 416000;2.吉首大学数学与统计学院,湖南 吉首 416000)
基于现有的均匀性测度公式,利用Langrange乘数法和Taylor公式得到二水平设计离散偏差和对称化L2偏差紧的下界,最后通过2个例子来验证其结论.
均匀设计;U型设计;离散偏差;对称化L2偏差;下界
均匀设计是计算机试验和稳健试验设计的一种很重要的方法,它有助于试验点遍及整个设计空间.均匀性测度在均匀设计的构造方面有重要的作用,各种偏差作为均匀性测度用来衡量均匀性的好坏,其中最为常用的偏差有离散偏差[1]和对称化L2偏差[2].因此,离散偏差和对称化L2偏差作为均匀性测度,寻找它们精确的下界是十分重要的.若一个下界可以达到,则称这个下界是紧的.许多研究者尽力去找这些偏差的下界,针对二水平部分因子设计,文献[1]给出了离散偏差的一个下界,文献[2-3]分别给出了对称化L2偏差的一个下界.笔者利用Langrange乘数法和Taylor公式获得了二水平离散偏差和对称化L2偏差紧的下界.
1 预备知识
记d(n;qs)为一具有n次试验、s个q水平因子的设计,其设计表可看成是n×s的矩阵d=(dij),其中每一列取{0,1,…,q-1}中的元素,d的每一行对应于一次试验,d的每一列对应于一个因子.若d(n;qs)的任一列中的所有的水平出现相同的次数,则称d(n;qs)为U型设计,即每个因子的每个水平在每一列中出现相同的次数.所有具有n次试验、s个q水平因子的U型设计的集合记为U(n;qs).设δij为设计d的第i行和第j行之间相应位置上相同元素的个数,对于任意的设计d∈U(n;2s),其离散偏差和对称化L2偏差分别记为DD(d;a,b),SD(d),它们分别可以通过以下表达式得到:
(1)
其中a,b为常数且a>b>0;
(2)
关于(1),(2)式的详述分别参见文献[1-2].
引理1[4]已知l为任意整数,如果d∈U(n;2s),那么
(3)
其中:w为r/k的整数部分;p,q满足p+q=k和pw+q(w+1)=r;k=n(n-1);r=n(n-2)s/2.
2 主要结论
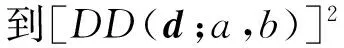
定理1 对任意的设计d∈U(n;2s),有
(4)
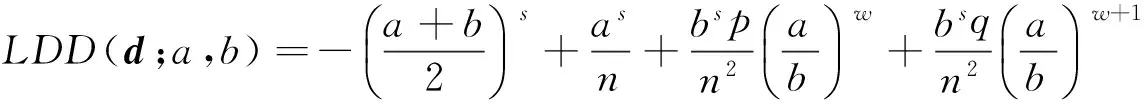
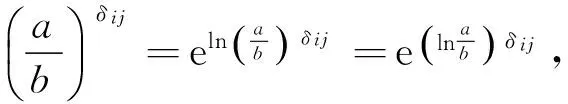
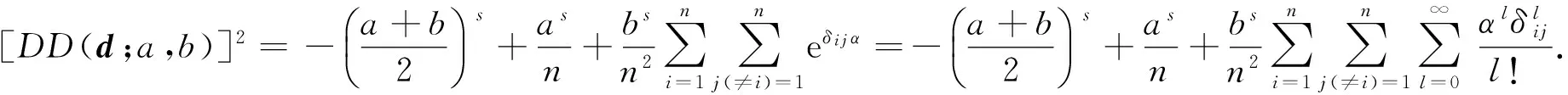
由(3)式可得
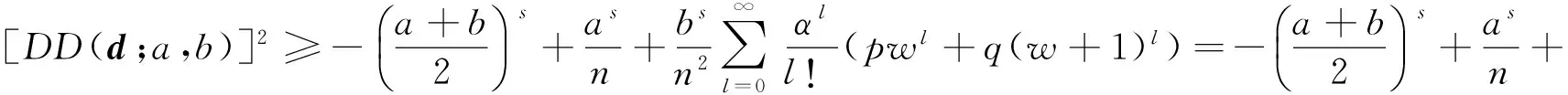
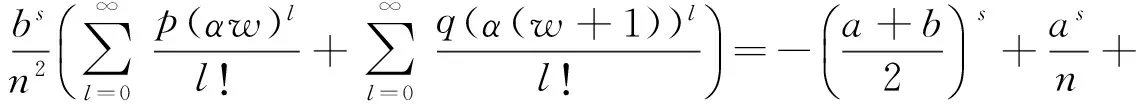
从而(4)式得证,定理1证毕.
定理2 对任意的设计d∈U(n;2s),有
(5)
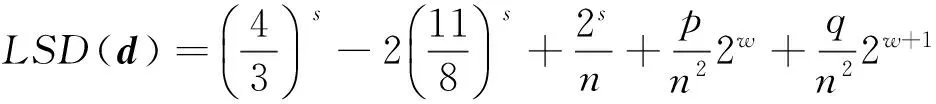
利用(3)式,可类似定理1的证明过程来完成定理2的证明.
3 举例
例1 考虑文献[5]中的2个设计d8,6∈U(8;26),d8,7∈U(8;27),其中n=8,s分别为6,7.表1分别给出了设计d8,6、d8,7、离散偏差(其中a=1,b=0.5)、对称化L2偏差及相应的下界.

表1 二水平设计d8,6、d8,7、离散偏差、对称化L2偏差及其下界
例2 考虑文献[5]中的2个设计d12,10∈U(12;210),d12,11∈U(12;211),其中n=12,s分别为10,11.表2分别给出了设计d12,10、d12,11、离散偏差(其中a=1,b=0.5)、对称化L2偏差及相应的下界.
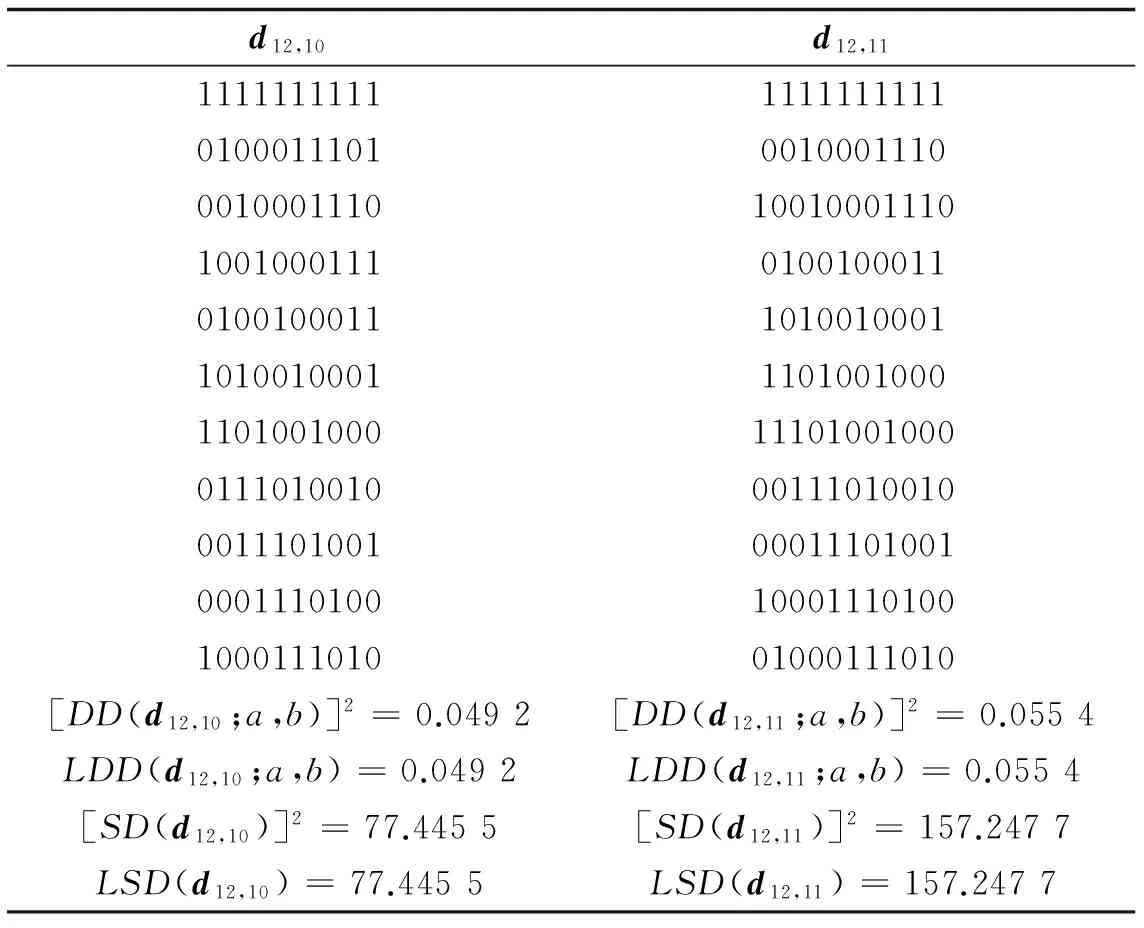
表2 二水平设计d12,10、d12,11、离散偏差、对称化L2偏差及其下界
从这2个例子不难发现,由(4)和(5)式求出的下界和相应的偏差的平方相等,这样的下界是最好的,且这2个下界可以达到,因此这2个下界都是紧的.
4 结语
基于已有的离散偏差和对称化L2偏差公式,利用Langrange乘数法和Taylor公式给出了二水平设计的离散偏差和对称化L2偏差紧的下界.
[1] QIN Hong,FANG Kaitai.Discrete Discrepancy in Factorials Designs[J].Metrika,2004,60:59-72.
[2] 汪政红.对称化L2偏差新的下界及其应用[D].武汉:华中师范大学数学与统计学学院,2006.
[3] FANG Kaitai,MA Changxing,MUKERJEE R.Uniformity in Fractional Factorials[M]//FANG Kaitai,HICKERNELLll F J,NIEDERRERTER H.Monte Carlo and Quasi ̄Monte Carlo Methods in Scientific Computing.Berlin:Springer,2002:232-241.
[4] CHATTERJEE K,LI Zhaohai,QIN Hong.Some New Lower Bounds to Centered and Wrap ̄AroundL2 ̄Discrepancies[J].Statistics and Probability Letters,2012,82:1 367-1 373.
[5] FANG Kaitai,WINKER P.Lower Bounds for Centered and Wrap ̄AroundL2 ̄Discrepancies and Construction of Uniform Designs by Threshold Accepting[J].Journal of Complexity,2003,19:692-711.
(责任编辑 向阳洁)
LowerBoundstoDiscreteDiscrepancyandSymmetricL2DiscrepancyinTwoLevelFractionalFactorialDesigns
LI Hongyi1,2,LI Qisheng2,OU Zujun2
(1.Normal College,Jishou University,Jishou 416000,Hunan China;2.College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)
On the basis of existing formula of uniformity measurement and using the Langrange multiplier method and the formula of Taylor,the tight lower bounds to discrete discrepancy and symmetricL2discrepancy of two level fractional factorial designs are obtained.Finally,two examples are given to illustrate the results.
uniform design;Utype design;discrete discrepancy;symmetricL2discrepancy;lower bound
1007-2985(2014)03-0020-03
2013-11-12
国家自然科学基金项目(11201177);湖南省教育厅科研项目(12C0287);湖南省教育厅优秀青年项目(14B146);吉首大学校级科研项目(13JDY041);吉首大学学成返校博士科研项目(JSDXXCFXBSKYXM201113)
李洪毅(1978-),女,湖南沅陵人,吉首大学数学与统计学院硕士研究生,主要从事概率统计研究
欧祖军(1979-),男,湖南宜章人,吉首大学数学与统计学院副教授,主要从事概率统计及试验设计研究;E ̄mail ozj9325@mail.ccnu.edu.cn.
O212.6
A
10.3969/j.issn.1007-2985.2014.03.005

