公路隧道结构计算的分项系数法

郭小红,舒 恒,拓勇飞

(中交第二公路勘察设计研究院有限公司,湖北 武汉 430056)

公路隧道结构计算的分项系数法

郭小红,舒 恒,拓勇飞

(中交第二公路勘察设计研究院有限公司,湖北 武汉 430056)

应用概率极限状态设计方法是当今国内外结构设计发展的必然趋势。为了推进分项系数法在公路隧道结构设计中的应用，结合隧道结构和分项系数法的特点，针对不同的隧道建设工法及结构安全等级，提出各分项系数的取值建议，并对各分项系数进行经验校准。得到如下结论：1)当隧道结构安全等级为一级时，根据本文给出的分项系数的计算结果，结构的总体安全水平略高于传统设计方法；2)当结构安全等级为二级时，其总体安全水平与传统设计方法相当；3)安全等级为三级时比传统方法略低。建议推行基于结构可靠度理论的分项系数法。本文对隧道设计规范修编具有较大的参考价值。

隧道结构；计算；可靠度；分项系数

0 引言

对于公路隧道结构计算，现行规范推荐采用基于破损阶段的安全系数法进行强度校核[1]。破损阶段法要求结构构件达到破损阶段时的承载能力R不低于标准荷载引起的结构内力S乘以安全系数K，即KS≤R。破损阶段法将影响结构安全的各种因素集中在一个安全系数中来考虑，但该安全系数由经验确定，没有理论及计算依据，未能考虑不同影响因素对结构安全性的影响，并不能真实反映结构的安全程度[2-4]。破损阶段法对素混凝土隧道支护结构具有一定合理性，但真正需要验算的结构是地质条件较差、大跨度条件下的钢筋混凝土结构，其合理性存在一定的局限。这就需要逐步改进，以求进一步完善结构设计理论。

20世纪40年代，美国学者Freudentha[5]提出了结构可靠性理论；至60—70年代，结构可靠性理论有了很大的发展；70年代以来，国际上结构可靠度理论在土木工程领域逐步进入了实用阶段[6-8]。我国从20世纪70年代中期才开始研究，但至20世纪80年代后期就在建筑结构领域率先进入了实用阶段，研究成果已应用于结构设计规范[9-14]。这些统一标准以结构可靠度理论为基础，采用以分项系数表达的概率极限状态设计方法，作为我国各行业结构设计规范修编的准则。

采用全概率法进行结构计算还处于研究阶段[15]，计算工作量太大且过于复杂，还不具备全面应用的条件。采用分项系数设计表达式，可以更好地考虑影响结构可靠度的各基本变量的变异性，更好地处理结构安全可靠度与经济合理性这一对基本矛盾，使所设计的各种结构构件在不同的设计条件下均具有较佳的可靠一致性。在隧道结构设计标准中采用概率极限状态设计原则和分项系数设计表达式，有利于促进隧道结构设计理论的发展，推动隧道结构设计标准的技术进步，更好地对结构中主要的不定性因素利用统计数学进行量化分析，为实现优化设计，在安全与经济之间选择最佳平衡创造条件。

在隧道结构设计中全面推行分项系数法在当前还有一定的困难，但是可以从第一步——经验校准法开始，为规范管理部门、规范编制者以及设计者今后有意识地去搜集和积累有关变量的统计资料，为今后隧道结构设计向以结构可靠度理论为基础的概率极限状态设计法转化创造条件。

1 现行规范强度校核方法与安全系数

现行《公路隧道设计规范》[1]及《公路隧道设计细则》[16]规定：公路隧道衬砌结构可采用砌体结构、混凝土结构或钢筋混凝土结构，应按破损阶段法对其正截面强度进行校核。

偏心受压砌体或混凝土结构的抗压强度按式(1)进行：

KN≤φαbhRa。

(1)

偏心受压混凝土结构的抗拉强度验算按式(2)进行：

KN≤1.75φRlbh/(6e0/h-1)。

(2)

轴心受压钢筋混凝土构件的正截面强度按式(3)进行：

(3)

受弯钢筋混凝土构件的正截面强度按式(4)进行：

(4)

式中：M，N为设计荷载作用下截面的弯矩及轴力；b，h，h0为矩形截面宽、高度及截面有效高度；φ，α为构件纵向弯曲系数、轴向力的偏心影响系数；Ra，Rl为混凝土抗压极限强度、混凝土抗拉极限强度；Rg′为纵向受压钢筋抗压强度标准值；A，Ag′分别为构件截面面积和纵向受压钢筋截面面积；x为混凝土受压区的高度；ag′为受压钢筋合力点至受压区边缘的距离。

在验算构件截面的强度时，规范要求根据不同的荷载组合，分别采用不同的安全系数K，并应不小于表1和表2给出的数值[1，16]。

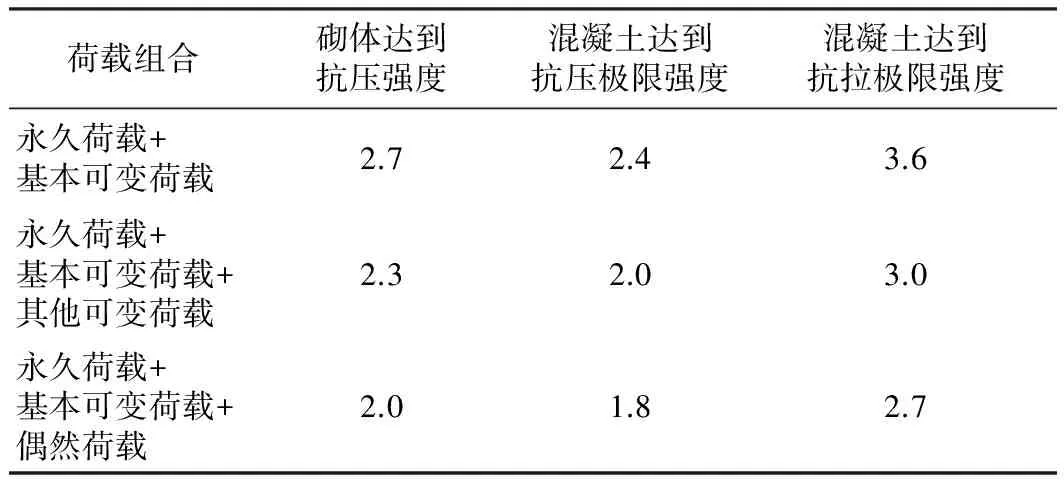
表1 混凝土和砌体结构的强度安全系数KTable 1 Safety factors of plain concrete and masonry structures K

表2 钢筋混凝土结构的强度安全系数KTable 2 Safety factors of reinforced concrete K

隧道支护结构在稳定洞室过程中起主要作用，承担外部荷载较明确，且自重荷载可能控制结构强度时，一般可以采用荷载-结构模型进行内力计算，并对其极限状态进行校核，如：明洞结构、棚洞结构、浅埋隧道衬砌结构、Ⅳ～Ⅵ级围岩深埋地段衬砌结构及特殊地质条件下的衬砌结构等，应进行支护结构内力计算及强度校核。经对前述公式及表格的分析可以看出，现行隧道设计规范在进行结构强度校核时，主要存在以下问题：

1)结构设计未充分考虑隧道的重要性。低等级公路隧道内交通量小，而高速公路隧道内交通量大，当隧道结构出现安全问题时，在社会上造成的影响以及产生的经济损失相差较大，按照当前结构设计理念，其安全系数或失效概率应该有差异。

2)未考虑隧道结构的施工方法差异对结构安全产生的影响。暗挖隧道由于施工条件差，且均为隐蔽工程，一般施工质量难以保证；如果采用预制构件，一般为工厂化生产，质量可靠性更好，而明挖隧道的施工质量则介于两者之间，在隧道结构设计过程中应有所反映。

3)土木工程技术发展迅速，新材料、新工艺层出不穷，需要合理考虑掘进机等新工法对荷载的影响及FPR筋材等新材料的使用等，采用传统的单一安全系数法进行结构强度验算已不能满足现阶段结构设计要求。

4)目前隧道结构强度验算方法与国内外其他土木工程行业相比落后较多，计算方法、计算参数与建设部及市政行业规范差异较大。对于一些重要工程，如水下隧道与市政隧道，由于建设单位、设计单位、施工单位以及行业主管单位可能来自于不同的行业，这些差异会给设计及管理带来极大不便。

根据上述分析，在隧道结构强度校核中引入分项系数法非常有必要。

2 隧道结构计算的分项系数法

公路隧道支护结构的极限状态可分为承载能力极限状态、正常使用极限状态和耐久性极限状态。承载能力极限状态可理解为结构或结构构件发挥允许的最大承载功能的状态，当隧道支护出现基础过大沉降、初期支护压屈或失稳、二次衬砌受力过大而开裂破坏、洞门滑移或失稳等现象时，应认为超过了承载能力极限状态；正常使用极限状态指结构因受力而使其几何形状、外观等发生显著改变，虽未达到最大承载能力，但已彻底不能使用，如隧道支护出现超过规定的收敛变形或差异沉降、未影响承载功能的开裂以及车道板震动过大等现象；耐久性极限状态为结构或构件在外部环境作用下，其承载功能或外观达到设计最低要求的状态，当隧道支护出现结构表面发生的损伤影响结构外观或损害结构承载力、钢筋锈蚀导致的顺筋裂缝，其性能接近设计指标时，应认为超过了耐久性极限状态。

根据公路工程相关规范[10]，进行持久状况承载能力极限状态设计时，公路隧道结构的目标可靠指标不应小于表3的规定指标。可靠度指标对应的失效概率如表4所示。

表3 公路隧道结构的目标可靠指标Table 3 Reliability index for highway tunnel structure

表4可靠度指标对应的失效概率
Table 4 Relationship between reliability index and failure probability

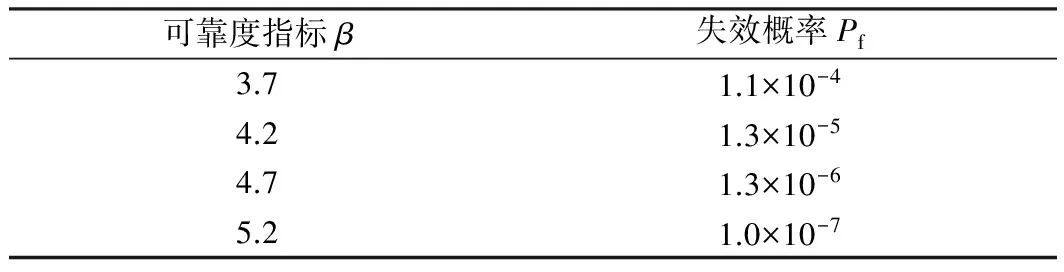
可靠度指标β失效概率Pf3．71．1×10-44．21．3×10-54．71．3×10-65．21．0×10-7

由表4可以看出，安全等级最低时，结构的失效概率约为万分之一，安全等级每提高一级，其失效概率则降低一个数量级。

基于极限状态的分项系数法可采用式(5)[16]表示。

γ0γ1S(γffr,αk)≤R(fk/γm,αk,C)。

(5)

式中：γ0，γ1为结构重要性系数及结构附加安全系数；S(.)为作用在结构之上的荷载作用效应函数；R(.)为与结构材料强度及几何尺寸相关的结构抗力效应函数；fr为作用在结构之上的作用组合标准值；fk，αk为结构材料性能，几何参数标准值；C为结构的极限约束值；γf，γm为荷载分项系数及结构材料性能的分项系数。

如何从确定的结构目标可靠度指标或容许失效概率推导出式(5)中的分项系数，是实现基于可靠度设计理论的分项系数法的关键所在。

3 分项系数的确定

3.1 分项系数的表达

当按设计值方法确定作用(荷载)分项系数时，永久作用分项系数γG、可变作用分项系数γQ和抗力分项系数γR可分别按式(6)、式(7)和式(8)确定：

(6)

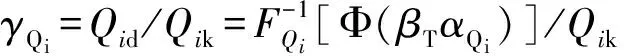
(7)

(8)

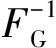
根据式(6)—(8)确定荷载分项系数非常复杂，且当前各基本变量的统计参数还不够完备，因此需要寻求其他的方法。

3.2 分项系数法的强度校核方法

根据混凝土及钢筋混凝土结构设计原理，隧道结构分项系数法的强度校核可采用以下方法进行。

偏心受压砌体或混凝土结构的抗压强度按式(9)进行：

γ0γ1Nf≤φαbh·fck/γck。

(9)

偏心受压混凝土结构的抗拉强度验算按式(10)进行：

γ0γ1Nf≤1.75φbh·ftk/γtk·(6e0/h-1)

(10)

轴心受压钢筋混凝土构件的正截面强度按式(11)进行：

γ0γ1Nf≤0.9φ(fck/γck·A+Rg′/γg·Ag′)

(11)

受弯钢筋混凝土构件的正截面强度按式(12)进行：

γ0γ1Mf≤fck/γck·bx(h0-0.5x)+Rg′/γg·Ag′

(12)

式中：fck，ftk分别为混凝土轴心抗压强度标准值和抗拉强度标准值；Mf，Nf为计算荷载(考虑荷载分项系数)作用下截面的弯矩及轴力；γck，γtk，γg分别为混凝土抗压强度分项系数、混凝土抗拉强度分项系数及钢材的强度分项系数。

3.3 分项系数法的校准方法

目前，隧道结构设计采用分项系数法还处于经验校准阶段。在进行结构强度校核时，要求采用式(9)—(12)设计的结构安全度不低于采用式(1)—(4)的水平。对上述2组公式进行对比以及参照相关行业规范就可初步确定其分项系数。

偏心受压砌体或混凝土结构的抗压强度：

γ0γ1γck·Ra/fck·Nf/N≥K。

(13)

偏心受压混凝土结构的抗拉强度：

γ0γ1γtk·Rl/ftk·Nf/N≥K。

(14)

轴心受压钢筋混凝土构件的正截面强度：

(15)

受弯钢筋混凝土构件的正截面强度：

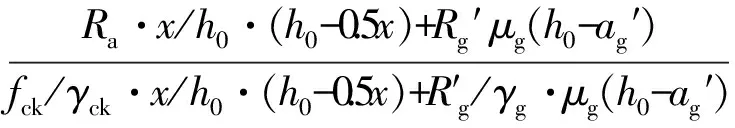
(16)

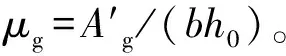
根据式(13)—(16)，参照现行行业标准与规范，可以对式(1)—(4)公式中的分项系数进行校准，确定各个分项系数。

4 分项系数的取值与校准

一般情况下，结构重要性系数γ0、结构材料性能的分项系数γm及荷载分项系数γf在各行业规范之中取值基本相当。按照隧道结构破坏可能产生的后果(危及人的生命、造成经济损失和产生社会影响等)严重程度，一般将隧道结构划分为3个安全等级。一级：高速公路、一级公路隧道、公路水下隧道、连拱隧道、三车道及以上跨度的公路隧道、长度L>3 000 m公路隧道及地下风机房；二级：双车道的二、三级公路隧道，长度L>1 000 m的四级公路隧道，斜井、竖井及联络风道等通风构造物；三级：长度L≤1 000 m的四级公路隧道，斜井、竖井及平行导坑等施工辅助通道。各级隧道的重要性系数取值见表5。

表5 结构重要性系数γ0Table 5 Importance factor γ0

根据本行业桥涵设计规范及相关行业结构设计规范的规定，隧道支护结构的材料性能的分项系数γm可按表6取值。

表6 材料的分项系数γmTable 6 Material factor γm

一般结构采用作用效应组合，不同的荷载组合其效应(内力)组合系数不同，因此其荷载分项系数也不相同。隧道支护结构由于地层弹性抗力的参与，荷载产生的内力具有高度非线性，因此一般不采用效应组合，宜采用荷载组合，即用荷载组合系数将各类荷载累加在一起，然后求解内力。对于一般的隧道支护结构，主要承担地层的岩土压力与水压力，均为静载，即使对于浅埋结构或汽车荷载作用显著的隧道结构，其动载在总荷载中比例很低，一般仅占总荷载的5%～10%，这样隧道荷载组合相对更为简单。

荷载组合的分项系数选取是一个非常复杂的工作，但是基于工程设计可以进行适当简化处理。参照相关行业规范[16-18]，结构的荷载分项系数为1.2～1.4，如果为恒载则取1.2，如果为动载则取1.4，然后根据荷载的分布特点进行适当调整；结构正常使用极限状态的荷载分项系数一般为0.5～1.0，如果为恒载则取1.0，如果为动载则取0.5～0.7；结构在偶然荷载作用下的承载能力极限状态的荷载分项系数一般取1.0。

鉴于公路隧道施工工法的多样性，分项系数中增加了一项结构附加安全系数γ1。结构附加安全系数γ1综合考虑结构施工的不确定性并与目标可靠度指标相联系，通过可靠性分析并适当考虑工程经验确定。由于公路隧道有关变量的统计资料积累还相对较少，本文根据工程经验选取合适的结构附加安全系数γ1，达到分项系数法与破损阶段设计法的安全度水平保持总体相当。采用钻爆法施工的隧道结构，由于施工环境比较差，隐蔽工程的质量控制难度大，因此其附加安全系数应适当提高；而对于采用工厂化预制生产的结构，由于其质量有充分保证，其附加安全系数可适当降低。隧道结构的附加安全系数γ1可按表7取值。

鉴于表7中的系数主要是针对二级及三级公路隧道提出的，并未根据隧道的重要性程度区别对待，因此对于安全等级为一级的高等级公路隧道及水下隧道，其结构安全要求更高一些，而部分安全等级为三级的低等级公路隧道的结构安全系数可以适当降低。总之，应据此实际情况进行安全系数的校核。

表7 结构附加安全系数γ1Table 7 Additional safety factor γ1

对于采用钻爆法施工的山岭公路隧道结构，重要性一般分为一级、二级与三级，混凝土强度等级一般采用C25、C30、C35，作为安全储备的混凝土结构厚度一般为30～35 cm，钢筋混凝土结构厚度一般为50～60 cm，钢筋强度等级一般采用HRB400。其安全系数校核情况见表8。

表8钻爆隧道钢筋混凝土结构安全系数校核
Table 8 Safety factor calibration for reinforced concrete structure of drill and blast tunnel

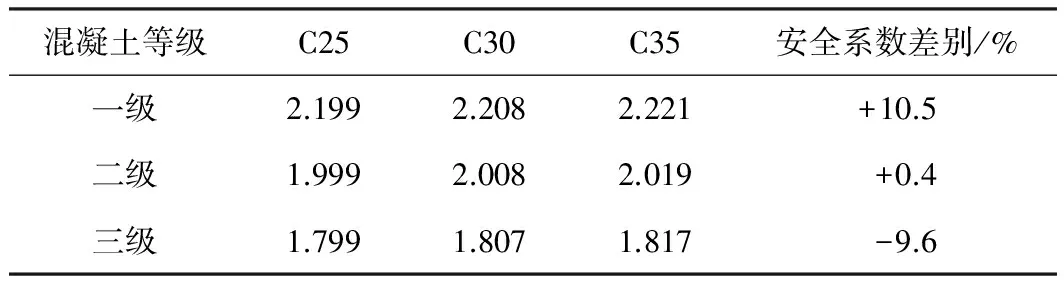
混凝土等级C25C30C35安全系数差别/%一级2．1992．2082．221+10．5二级1．9992．0082．019+0．4三级1．7991．8071．817-9．6

从分项系数换算得到的综合安全系数可以发现：对于钢筋混凝土结构，当结构安全等级为二级时，其安全系数与传统方法相当；安全等级为一级的结构安全系数比传统方法要求高约10%；安全等级为三级的隧道结构将比传统方法要求低约10%。主要原因是同类设计规范中混凝土结构的抗压分项系数取值偏低。对于安全等级为一级的隧道，采用混凝土作为承载结构时对其要求较二级、三级隧道更高，符合工程质量的控制规律。

对于明挖隧道及棚洞结构，重要性一般为一级或二级，混凝土强度等级一般采用C25、C30、C35，结构厚度一般为60～100 cm，钢筋强度等级一般采用HRB400。其安全系数校核情况见表9和表10。

表9一级明洞结构安全系数校核
Table 9 Safety factor calibration for Grade I cut-and-cover tunnel structure

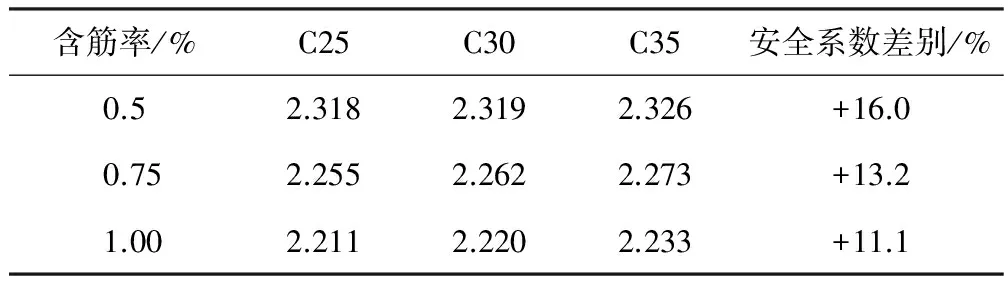
含筋率/%C25C30C35安全系数差别/%0．52．3182．3192．326+16．00．752．2552．2622．273+13．21．002．2112．2202．233+11．1

从计算结果可以发现：对于明挖隧道及棚洞结构，当结构安全等级为二级时，其安全系数与传统方法相当；安全等级为一级的结构安全系数比传统方法要求高约13%，符合工程质量的控制规律。

表10二级明洞结构安全系数校核
Table 10 Safety factor calibration for Grade II cut-and-cover tunnel structure

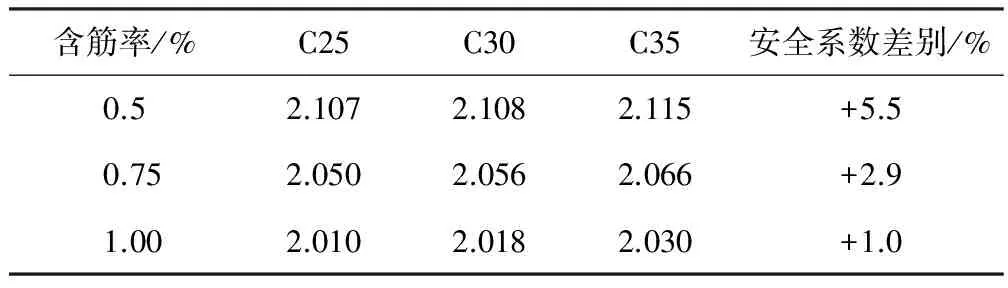
含筋率/%C25C30C35安全系数差别/%0．52．1072．1082．115+5．50．752．0502．0562．066+2．91．002．0102．0182．030+1．0

盾构隧道结构重要性一般为一级，混凝土强度等级一般采用C45、C50、C60,结构厚度一般为45～65 cm，钢筋强度等级一般采用HRB400。其安全系数校核情况见表11。

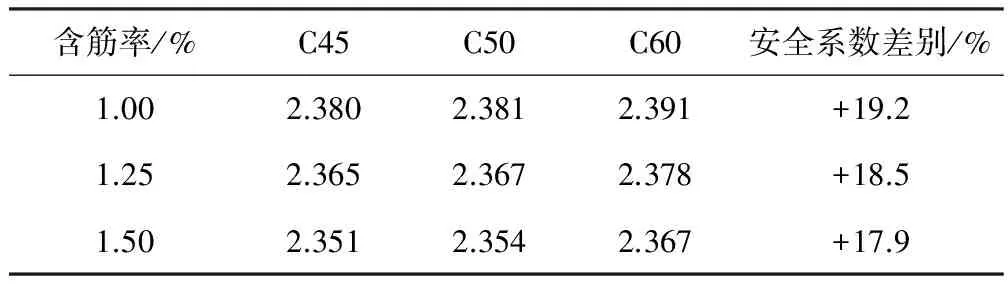
表11 盾构隧道结构安全系数校核Table 11 Safety factor calibration of shield tunnel structure

沉管隧道结构重要性一般为一级，混凝土强度等级一般采用C35、C40、C45，结构厚度一般为100～120 cm，钢筋强度等级一般采用HRB400。其安全系数校核情况见表12。

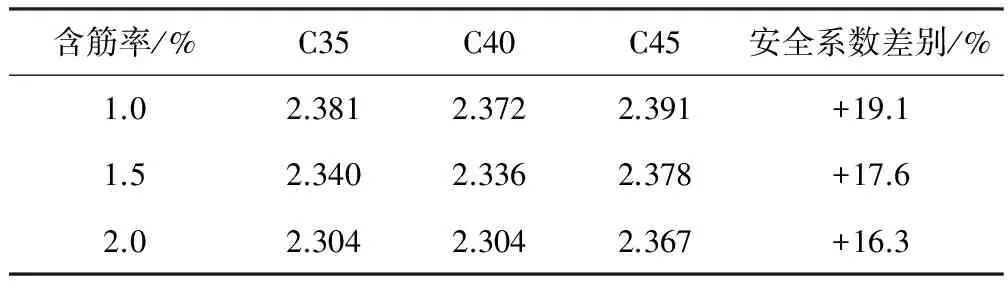
表12 沉管隧道结构安全系数校核Table 12 Safety factor calibration of immersed tunnel structure

通过计算发现，对于盾构及沉管隧道，按目前给定的分项系数进行结构验算，其综合安全系数要求达到2.3～2.39。鉴于该类隧道的重要性，其安全系数应该由传统的2.0提升至2.2(重要性系数1.1)，因此分项系数的取值是合理的。同时通过计算分析发现，当水压力比例增加时，综合安全系数将降低。对于水下盾构隧道，如果水压力所占比例达到50%左右，综合安全系数接近2.1；对于水下沉管隧道，如果水压力所占比例达到70%，则综合安全系数接近2.0。

5 结论

在工程结构设计标准中采用以结构可靠度理论为基础的概率极限状态设计法，已成为国内外工程结构领域的发展趋势，国内土木工程界已作了大量工作，并取得了突破性的进展。在隧道结构设计标准中推行该方法，可以较好地对设计中主要的不确定性因素进行量化分析，为实现设计优化、在安全与经济之间选择最佳平衡创造条件。因此，在我国隧道结构设计标准中应积极推行以结构可靠度理论为基础的概率极限状态设计法。

本文结合分项系数的计算方法以及隧道结构的特点，针对不同的隧道建设工法及结构安全等级，提出了各分项系数的取值方法，并对各分项系数进行了经验校准。根据本文给出的各分项系数，荷载分项系数不低于1.35时，对于承载能力极限状态，安全等级为一级的结构，其总体安全度略高于传统设计；结构安全等级为二级的结构，其总体安全度与传统设计相当；安全等级为三级的结构，其总体安全度略低于传统设计。本文的研究结论对隧道设计规范的修订具有较大的参考价值。

[1]JTG D70—2004 公路隧道设计规范[S].1版.北京：人民交通出版社,2004.

[2]赵国藩,曹居易,张宽权.工程结构可靠度[M].北京:水利电力出版社，1984.(ZHAO Guofan,CAO Juyi,ZHANG Kuanquan.Reliability of engineering structures[M].Beijing:Hydraulic and Electric Power Press,1984.(in Chinese))

[3]杨伟军,赵传智.土木工程结构可靠度理论与设计[M].北京：人民交通出版社,1999.(YANG Weijun,ZHAO Chuanzhi.The reliability theory and design of civil engineering[M].Beijing:China Communications Press,1999.(in Chinese))

[4]魏新欣,丁文其.公路隧道概率极限状态设计方法[J].公路交通科技,2011,28(10):75-79.(WEI Xinxin,DING Wenqi.Probabilistic limit state design method of highway tunnel [J].Journal of Highway and Transportation Research and Development,2011,28(10):75-79.( in Chinese))

[5]A M Freudenthal,The safety of structures[J].Transactions of the American Society of Civil Engineers,1947,112(1):3-9.

[6]ACI 318—02 Building code requirements for structural concrete[S]．American Concrete Institute，2002.

[7]U S Department of transportation federal highway administration.Technical manual for design and construction of road tunnels [S]．National Highway Institute,2009．

[8]European committee for standardization.EN1997-1:2004 Eurocode7:Geotechnical design-part 1：General rules[S].2004.

[9]GB 50153—2008 工程结构可靠性设计统一标准[S].北京：中国建筑工业出版社,2009.(GB 50153—2008 Unified standard for reliability design of engineering structures[S].Beijing:China Construction Industry Press,2009.(in Chinese))

[10]GB/T50283—1999 公路工程结构可靠度设计统一标准[S].北京：中国计划出版社,1999.(GB/T50283—1999 Unified standard for reliability design of highway engineering structures [S].Beijing:China Planning Press,1999.(in Chinese))

[11]GB 50216—1994 铁路工程结构可靠度设计统一标准[S].北京：中国计划出版社,1994.(GB 50216—1994 Unified standard for reliability design of railway engineering structures[S].Beijing:China Planning Press,1994.(in Chinese))

[12]GBJ 68—2001 建筑结构可靠度设计统一标准[S].北京：中国建筑工业出版社,2001.(GBJ 68—2001 Unified standard for reliability design of building structures[S].Beijing:China Construction Industry Press,2001.(in Chinese))

[13]GB 50158—2010.港口工程结构可靠性设计统一标准[S].北京：中国计划出版社,2010.(GB 50158—2010 Unified standard for reliability design of port engineering structures[S].Beijing:China Planning Press,2010.(in Chinese))

[14]GB 50199—1994 水利水电工程结构可靠度设计统一标准[S].北京：中国计划出版社,1994.(GB 50199—1994 Unified standard for reliability design of hydraulic engineering structures [S].Beijing:China Planning Press,1994.(in Chinese))

[15]郭小红.厦门翔安海底隧道风化槽衬砌结构可靠度分析[J].隧道建设,2011,31(4):411-415.(GUO Xiaohong.Analysis on reliability of lining structure in weathering slot:Case study on Xiang’an subsea tunnel in Xiamen [J].Tunnel Construction,2011,31(4):411-415.(in Chinese))

[16]JTG/T D70—2010公路隧道设计细则[S].北京：人民交通出版社,2010.(JTG/T D70—2010 Guidelines for design of highway tunnel[S].Beijing:China Communications Press,2010.(in Chinese))

[17]GB 50009—2012 建筑结构荷载规范[S].北京：中国建筑工业出版社,2012.(GB 50009—2012 Load code for the design of building structures[S].Beijing:China Construction Industry Press,2009.(in Chinese))

[18]JTG D60—2004公路桥涵设计通用规范[S].北京：人民交通出版社,2004.(JTG D60—2004 General code for design of highway bridges and culverts[S].Beijing:China Communications Press,2004.(in Chinese))

PartialFactorMethodforStructureCalculationofHighwayTunnels

GUO Xiaohong,SHU Heng,TUO Yongfei

(CCCCSecondHighwayConsultantsCo.,Ltd.,Wuhan430056,Hubei,China)

It is a worldwide inevitable trend to adopt probability limit state design method in the structure design.In order to promote the application of partial factor method in the structure design of highway tunnels,the authors make proposals on the partial factors,considering the characteristics of the tunnel structure and the partial factor method,as well as considering the tunnel construction method and the structure safety grade.The authors also make calibrations on these partial factors on basis of experiences.Conclusions drawn are as follows:1) For tunnel structures with Grade I safety level,the total safety factor obtained by partial factor method is higher than that obtained by traditional design method; 2) For tunnel structures with Grade II safety level,the total safety factor obtained by partial factor method is almost the same as that obtained by traditional design method; 3) For tunnel structures with Grade III safety level,the total safety factor obtained by partial factor method is slightly lower than that obtained by traditional design method.The authors propose that the partial factor method based on reliability theory should be adopted in the new standards,specifications and codes.The paper can provide reference for the revision of the tunnel design standards in the future.

tunnel structure; calculation; reliability; partial factor

2014-01-27;

2014-03-24

郭小红(1966—)，男，湖南澧县人，1989年毕业于同济大学，地下工程与隧道工程专业，博士，教授级高级工程师，从事隧道及地下工程设计与研究工作。

10.3973/j.issn.1672-741X.2014.05.002

U 459.2

A

1672-741X(2014)05-0402-06