新型三维形貌测量系统SIFT算法改进研究*

刘常杰,黄东晓,杨凌辉

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)



新型三维形貌测量系统SIFT算法改进研究*

刘常杰,黄东晓,杨凌辉*

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)

将测绘领域的三线阵摄影测量原理应用于运动物体三维形貌测量,提出一种基于三线阵CCD的新型三维形貌测量方法。针对新型测量系统获取的三线阵CCD影像同名点匹配问题,研究了常用的影像匹配算法,并选用SIFT匹配算法。由于传统SIFT匹配算法处理大尺寸图像耗时长、提取匹配点数少等不足,对算法进行优化,并提出基于新型大尺寸三维形貌测量系统的匹配搜索策略,确定最优匹配阈值,最后通过对比实验进行验证。实验表明,改进的算法能够解决匹配影像视角变化等问题,缩短算法处理时间,增加匹配点数,提高算法性能。

三维形貌测量;三线阵CCD;SIFT算法;影像匹配

连续运动物体三维形貌检测问题在隧道施工维护、高速列车安全检测等方面广泛存在[1]。在二维图像分析基础上引入三维形貌信息,是该领域研究最具吸引力的思路,三维信息和二维信息的相互补充和校核,可以确保检测信息完整性、结果可靠,但其对测量提出大尺度、高动态、高分辨率、实时性好等特殊测量要求[2-4]。目前关于运动物体三维形貌及表面检测的研究相对较少。德国Otto Hofmann博士[5]提出三线阵CCD传感器摄影测量原理,常应用于遥感测绘领域,但该系统复杂度高、对数据无法进行在线处理。本文借鉴该思想通过运动信息将传感器输出的连续时间图像序列与空间相对姿态关联融合,创新一种大尺寸运动物体三维形貌测量方法,并设计了相关测量系统。

测量中三个不同拍摄视角的线阵CCD匀速运动获取线阵影像。由于存在遮挡、光照变化等干扰因素,而灰度匹配易受其影响,图像理解匹配算法不成熟,故选用SIFT尺度不变特征变换(Scale-Invariant Feature Transform)点特征匹配算法[6-8]。该算法对光照变化、尺度变化、视角变化和旋转等具有一定的不变性,同时具有鲁棒性强、独特性好、多量性、可扩展性等优点。目前常用于遥感测绘领域,但其匹配速度慢、效率低,不能直接应用于实时性高的场合,需对算法进行改进,实现对图像的高效匹配处理[9]。

对SIFT算法的改进一般是通过降维、结合图像其他特征等进行,陈文宇[10]使用圆区域描述特征子,具有较好的旋转不变性;冯嘉[11]使用PCA技术降低特征向量维度,减小算法计算量;王军铎等[12]将SIFT与小波金字塔进行结合,提高匹配正确率;张卡等[13]提出基于SIFT特征和灰度特征的综合匹配相似性测度计算方法,提高匹配精确度等等。改进算法一般仅在SIFT基础上进行,没有针对具体系统及应用场合进行优化,同时无法实现实时处理。

此外为确保本系统检测的可靠性,若获取的单幅影像大小为5 734×4 096像素,其要求匹配算法能够提取大量同名点、实时性好(百秒级)等,而传统SIFT算法耗时较长(千秒级)、提取同名点数量较少[14]。

针对上述问题及需求,本文依据前人对SIFT算法的改进思想,结合系统应用背景,对SIFT算法的三个耗时环节进行改进:优化尺度空间建立;简化特征描述子;采用基于系统的匹配搜索策略,从而降低SIFT算法的运算复杂度及计算量,提高匹配速度。此外选择合适匹配阈值,最终提高基于本系统的SIFT算法的匹配性能。

1 新型运动物体三维形貌测量系统

新型大尺寸三维形貌测量系统由计算机、三线阵CCD图像传感器、机械结构部分、电气驱动部分等组成。

针对测量成像要求,选用线阵CCD作为系统的成像单元,具有成本低、扫描精度高、分辨率高、视场大、易于实现动态测量等优点,能够克服面阵CCD像元数多、帧幅率受限等缺点。

线阵CCD数量选择及结构方面,选用三线阵CCD并采用相互平行且具有一定交会角的结构,扫描拍摄方向与CCD垂直。该结构能够解决单线阵CCD信息获取不完整、双线阵CCD易受表面遮挡影响等问题,实现被测量对象三维表面形貌的完整成像,满足测量要求。

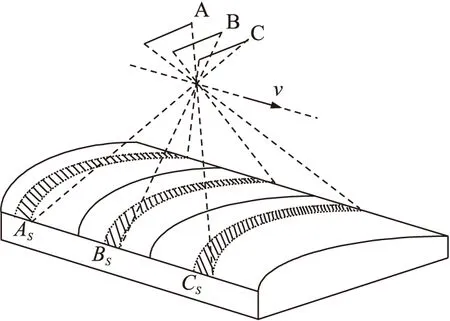
图1 新型大尺寸三维形貌测量原理

运动物体三维形貌测量原理与高分辨率遥感卫星测量基本原理相同,但是成像影像因素更多,对实时性要求更高。

测量时,三线阵CCD传感器载体在高精度直线导轨以垂直线阵CCD方向匀速运动,每个CCD以同步扫描周期对测量目标表面进行扫描拍摄,得到同一物体形貌不同透视中心的三个重叠影像[15]。如图1所示,A为前视传感器,B为正视传感器,C为后视传感器。三线阵CCD传感器以速度v匀速直线运动时间t后,分别扫描得到不同视角下的As、Bs、Cs三幅影像。

此后对所获取不同视角下重叠的CCD影像进行特征提取、匹配等,确定不同影像对应同名像点坐标;又三线阵CCD相机的内外方位元素可通过实验室标定确定,依据摄影测量前方交会公式,便能求出被测量对象表面物点的空间三维坐标,进而构建出被测物表面三维形貌。

2 SIFT算法原理

SIFT算法最早由Lowe D G于1999年提出的[16]。2004年,Lowe D G对其进行改进并正式提出[17]。SIFT特征匹配算法是目前国内外特征点匹配研究领域的热点和难点,其匹配能力强,可以处理两幅图像之间存在平移、旋转、视角变化、仿射变换、光照变化、噪声情况下的匹配问题。

SIFT算法实现影像匹配的主要有以下六个步骤:尺度空间的构造、尺度空间极值检测、特征点精确确定、特征点方向分配、生成特征点描述子、特征点匹配。

①尺度空间的构建。首先对图像I(x,y)构建高斯尺度空间,如式(1)所示;其次为有效在尺度空间检测到稳定的关键点,也为缩短时间和空间的复杂度,在构建高斯尺度空间的基础上构建高斯差分尺度空间如式(2)所示。

L(x,y,σ)=G(x,y,σ)×I(x,y)

(1)

D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]×I(x,y)=L(x,y,kσ)-L(x,y,σ)

(2)

其中:G(x,y,σ)为变尺度的高斯函数,k为两相邻尺度空间倍数的常数。

②尺度空间极值点检测。尺度空间中极值点的寻找是在高斯差分金字塔中进行,对于图像中的每个采样点必须与同一尺度及相邻两尺度的相邻的26个采样点进行比较,如果该采样点小于或大于这26个相邻点,则该点为一个局部极值点。

③特征点精确定位。由于检测极值点是在离散空间进行,其并非真正意义上的极值点,因而需要通过Taylor二次多项式曲面拟合方法以精确确定特征点的位置和尺度坐标,同时去除对比度低的极值点和不稳定的边缘响应点,以增强匹配稳定性、提高抗噪能力。

④特征点方向分配。为了实现图像旋转不变性,采用直方图统计方法,利用特征点的局部图像梯度方向特性,为特征点指定方向参数。

M(x,y)=√{[L(x+1,y)-L(x-1,y)]2+[L(x,y+1)-L(x,y-1)]2}

(3)

θ(x,y)=arctan{[L(x+1,y)-L(x-1,y)]/[L(x,y+1)-L(x,y-1)]}

(4)

式(3)和式(4)为(x,y)处为梯度的模和方向;L所用的尺度为每个特征点各自所在的尺度。

⑤特征点描述子生成。为确保旋转不变性,首先将坐标轴旋转为特征点的方向;之后以特征点为中心取大小为16×16的像素区域,并将其等间隔分为4×4大小的子区域,每个子区域生成有8个方向的梯度强度信息的种子点,因此每个特征点有4×4共16个种子点组成,即共有4×4×8个数据,最终形成128维SIFT特征向量。

⑥特征点匹配。为获得两幅图像间的同名点对,采用欧式距离法,取左影像中某个特征点,通过遍历找出其与右影像中所有特征点的欧式距离最近的前两个特征点,若距离的比值小于某个比例阈值,则接受这一对匹配点。

3 算法改进

新型大尺寸三维形貌测量系统获取的影像数据量大,而传统SIFT算法处理大尺寸影像时耗时长、性能低,需要对算法进行改进,提高实时性。

通过对大量影像的SIFT匹配试验及分析[18],统计SIFT匹配算法各个阶段所需要的时间占总时间的百分比,如表1所示。

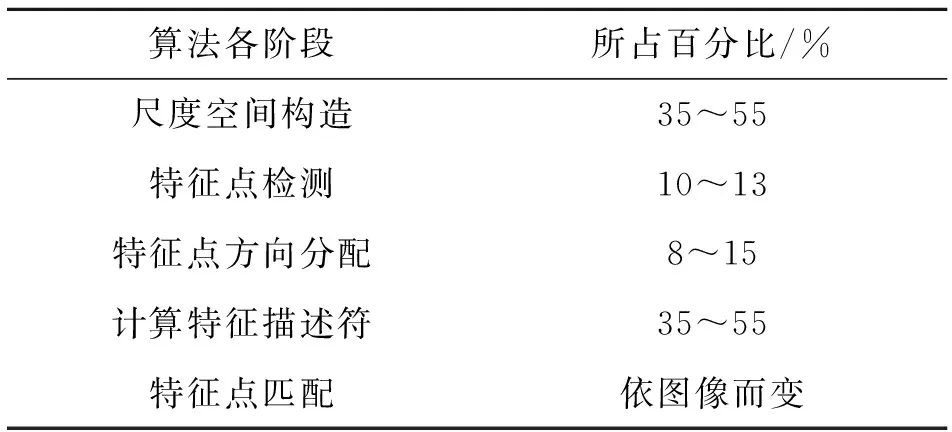
表1 SIFT匹配算法各阶段所需时间

从表1我们可以发现,尺度空间构造及特征描述符的生成耗时比例大,特征点匹配则与搜索策略和图像匹配区域有关。因而下文在将从这几方面对SIFT算法进行优化。

3.1 优化尺度空间构建

传统的SIFT算法对高斯金字塔一般会构建8组以上,每组有3～5层。组数和层数的选择直接影响到整个算法的精准性和复杂程度。通过试验发现,80%以上的特征点分布在金字塔的第一组和第一层,15%以上的特征点分布在金字塔第一组第二层。此外高分辨率三线阵CCD获取的影像尺寸较大,在保证能提取足够特征点的前提下,将构建的高斯金字塔进行简化,采取图像组数为3组,每组为5层。

3.2 简化特征点描述子

传统SIFT算法采用128维特征点描述子,虽能增强匹配稳健性,但与此同时也耗费了大量的时间,维度与耗时成正比;此外三线阵影像尺寸随扫描时间的增加,影像尺寸增大,提取的特征点数量增多,匹配的时间成本增加[19]。因此需要对特征点描述子的生成进行简化。

本文对特征点描述子的简化主要是通过减少种子点数、降低其特征向量维度实现。取窗口为以特征点为中心的8×8的像素区域,每4×4的窗口内计算出8个方向直方图,获得4×8共32维特征点描述子来表示特征点,如图2所示。

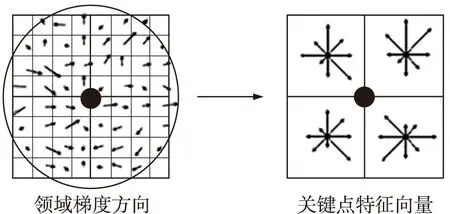
图2 特征点描述子的生成

3.3 基于三线阵CCD的匹配搜索策略

影像匹配算法的性能主要体现在速度、精度和可靠性三个方面。为加快匹配速度,可通过缩小匹配搜索窗口来提高搜索效率,减少非匹配点上的相关计算,即算法计算量,缩短运算时间,提高匹配效率。搜索窗口确定方法如下:

三线阵CCD以扫描方式对测量工件表面某一点P的成像过程如图3所示。前视与正视线阵CCD光学中心在y轴方向偏差为σ,两线阵CCD之间的垂直距离为s。在t1时刻,前视CCD(A)对物点P成像,当三线阵CCD在高精度平行导轨上直线运动时间t后,正视CCD(B)对物点P成像。取正视影像特征点(x1,y1)为已知,假设其前视影像匹配点为(x2,y2),则根据三线阵CCD成像特点,有:

x2=[x1-(l-s)×ε]∈[x1-((H+δ)tanα-s)×ε,
x1-((H-δ)tanα-s)×ε]

(5)

y2∈[y1-σ,y1+σ]

(6)

其中:H为三线阵CCD的工作距离;δ为物体表面物点最低点与最高点垂直距离;ε为CCD相机单位扫描距离对应像面空间的像元数,通过相机标定获得。

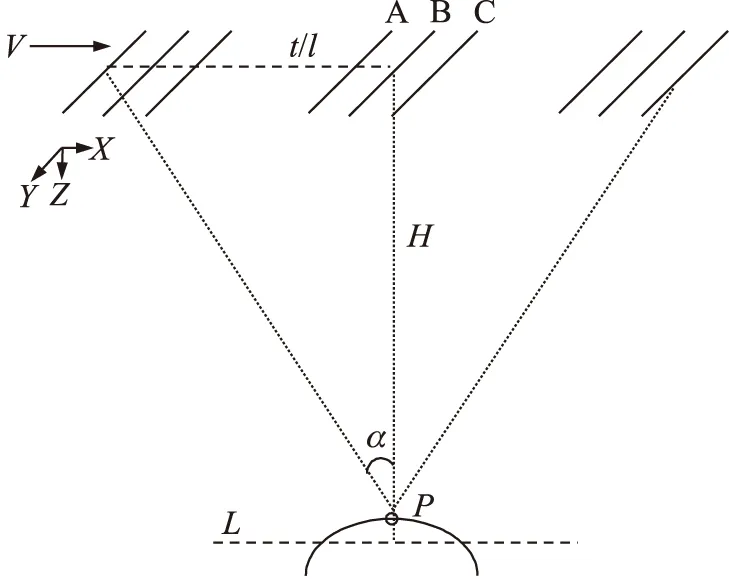
图3 三线阵CCD对P点成像过程

即利用三线阵CCD的结构及成像特点等,由式(5)、式(6)确定动态搜索窗口,从而使得进行影像匹配运算时,尽量减少无关计算量参与,提高匹配效率。正视与后视、前视与后视影像匹配搜索策略,同前视与正视的相似,不再赘述。

4 实验

为验证传统SIFT算法改进后的实时性及性能等,本文设计并采用基于三线阵CCD的新型三维形貌测量系统进行动态测量,获取三线阵影像,其成像部分如图4所示。

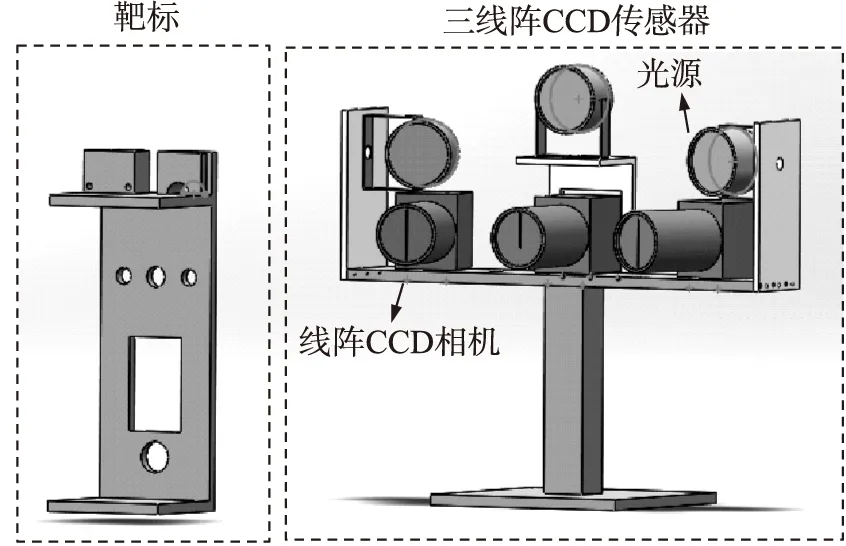
图4 三线阵CCD三维形貌测量示意图

其中,线阵相机选用Spyder3 SG-14,线阵CCD为2×4 096像素,相机焦距为50 mm,交会角为15°,工作距为650 mm。三线阵影像为三线阵传感器在高精度平行直线导轨上匀速运动(50 mm/s)对静止测试靶标扫描拍摄获得,影像大小为5 734×4 096像素。如图5所示。

将所获取的三幅影像进行分组匹配对比实验。实验一为改进SIFT算法和传统SIFT算法的对比试验;实验二为不同阈值下改进算法的对比试验;通过RANSAC进行提纯,确定正确率。

①实验一,SIFT算法进行影像匹配主要有六个步骤,本文对其中的尺度空间构建、特征点描述子生成、影像匹配三个步骤进行改进,目的是在匹配点数、正确率与算法处理时间进行权衡,验证改进算法的性能。匹配比例阈值选用0.6,实验结果如表2和表3所示。

图5 三线阵CCD前/正/后视影像

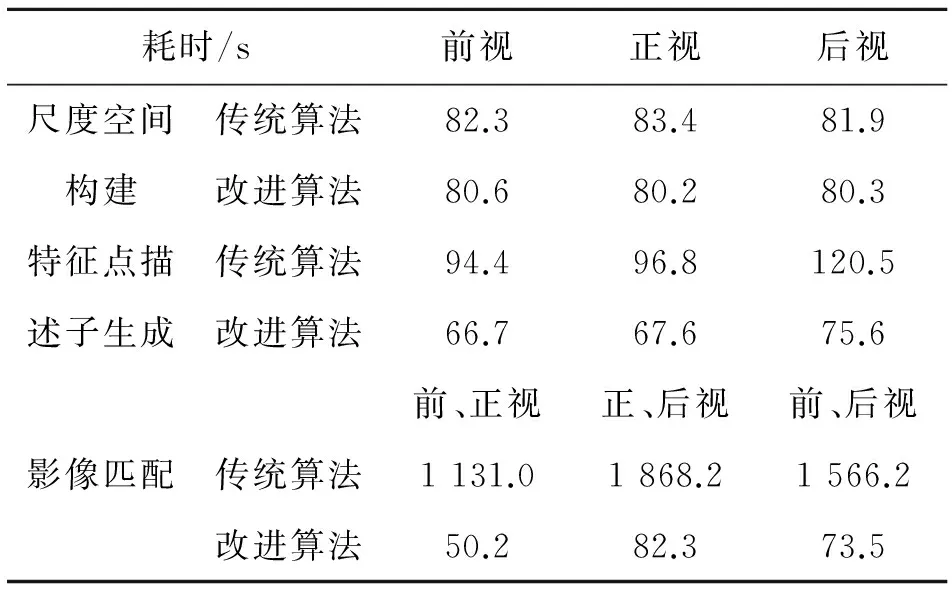
表2 SIFT算法耗时比较

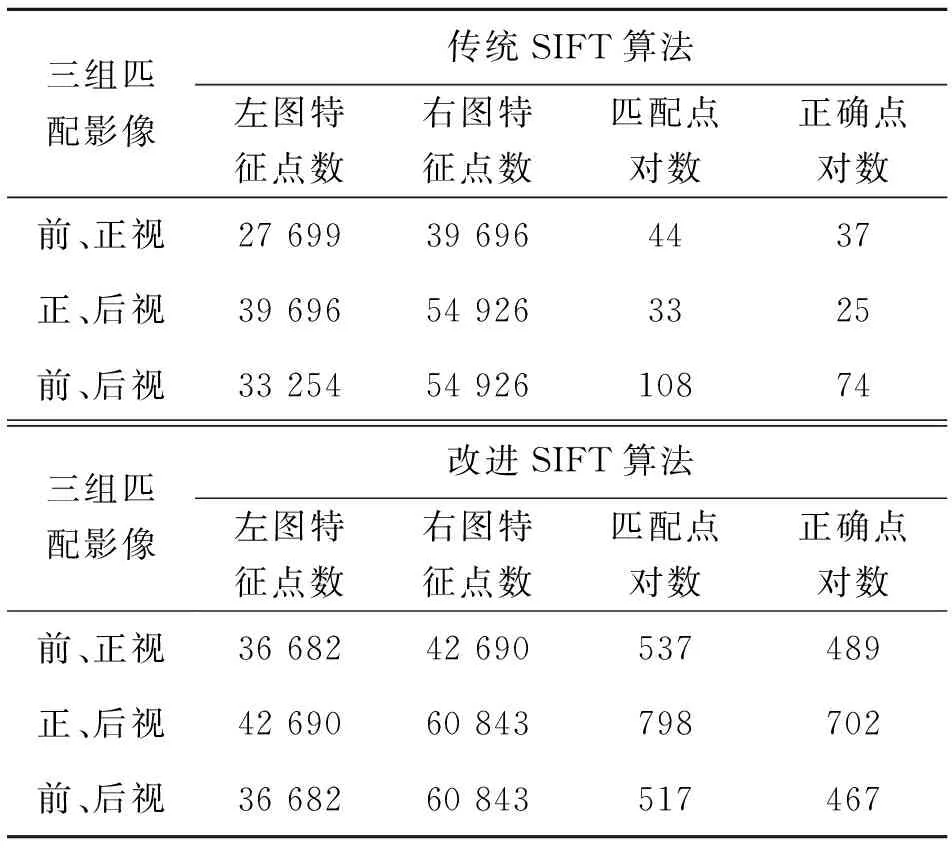
表3 算法改进前后匹配结果比较

实验结果表明,改进的SIFT算法缩短了尺度空间建立时间,同时也大大缩短了特征点描述子生成时间和匹配时间,并提高了匹配点数和正确率,解决不同视角下匹配问题,如前正视夹角为15°,前后视夹角为30°。改进的SIFT算法能够有效提高三线阵CCD影像的匹配效率和实时性。

②实验二,为了验证不同匹配阈值对于改进的SIFT算法在三线阵影像匹配中的影响,并选用合适的比例阈值,本文选用比例阈值为0.3/0.4/0.5/0.6/0.7,并对其进行实验对比,实验结果如表4和图6所示。

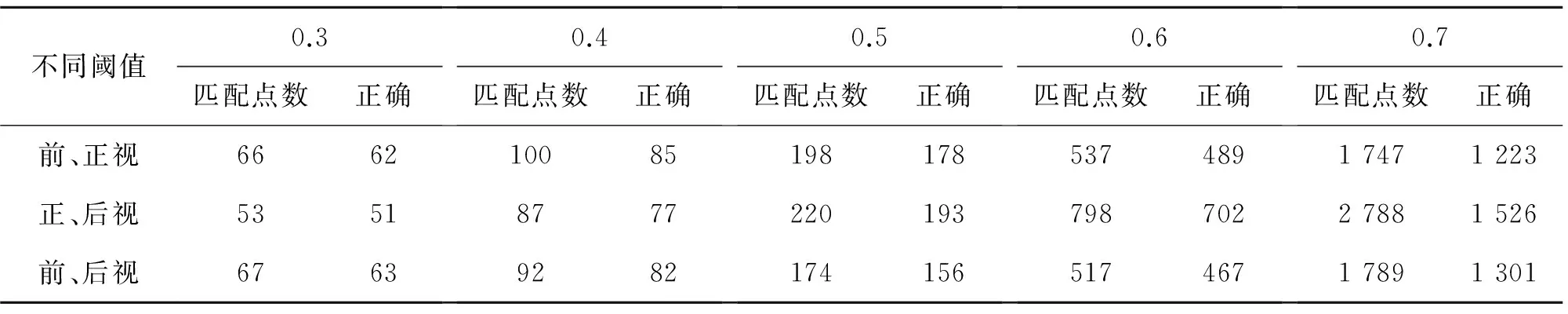
表4 不同阈值下的改进算法匹配结果

实验结果表明,阈值越大,影像匹配点数越多,同时误匹配情况也增多,但总体正确匹配点数也增多;阈值越小,影像匹配越稳定,但匹配点数量不足。而后续测量工件三维形貌重建,要求正确的匹配点多且稳定,因此,需要在匹配点数与稳定性间进行权衡,选择合适的阈值。经匹配对比实验,比例阈值选用0.6,可以在保证足够匹配点数的同时,得到较稳定的匹配结果,其部分匹配同名点连线图如图6所示。

图6 三组影像匹配结果(阈值为0.6)

5 结束语

本文提出新型的动态物体三维形貌测量方法,并针对系统改进了SIFT匹配算法,通过对比实验进行验证。实验结果表明,改进算法解决了不同视角匹配问题,提高了算法的实时性,匹配效率提高了一个数量级;匹配阈值与匹配点数及误匹配数成正比,在权衡匹配点数及正确率后,选用适合本系统的匹配阈值为0.6。因此,该匹配方法能够应用于对实时性、高分辨率等具有一定要求的运动物体三维形貌测量。

[1] 文强. 国内外高速列车检修制度综述[J]. 国外铁道车辆,2014,51(2):1-3.

[2]何华武. 高速铁路运行安全检测监测与监控技术[J]. 中国铁路,2013(3):1-7.

[3]Peisen S,Huang,Zhan Chenping,et al. High-Speed 3-D Shape Measurement Based on Digital Fringe Projection[J]. Opt Eng,2003,42(1):163-168.

[4]刘常杰,刘洋,刘邈,等. 光栅投影测量系统三维形貌拼接技术研究[J]. 传感技术学报,2014,27(7):870-875.

[5]王任享. 三线阵CCD影像卫星测量原理[M]. 北京:测绘出版社,2006.

[6]张会章,张利霞,郭雷. 图像理解[J]. 计算机工程,2003,29(11):23-24,71.

[7]赵斐,胡莘,关泽群,等. 三线阵CCD影像的像点自动匹配技术研究[J]. 测绘科学,2008,33(4):12-14,44.

[8]邓传斌,郭雷,李维. 基于SIFT的遥感图像配准方法[J]. 传感技术学报,2009,22(12):1742-1747.

[9]薛顺瑞,高原,唐湘成,等. 基于FPGA并行处理SIFT算法特征点检测[J]. 电视技术,2012,36(23):188-192.

[10]Chen Wenyu,Zhao Yanli,Xie Wenzhi,等. An Improved SIFT Algorithm for Image Feature-Matching,Multimedia Technology(ICMT)[J]. 2011 International Conference,2011,197(200):26-28.

[11]冯嘉. SIFT算法的研究和改进[D]. 吉林:吉林大学,2010.

[12]王君铎. 基于CCD影像数据构建DEM关键技术的研究[D]. 天津:天津理工大学,2012.

[13]张卡,盛业华,叶春. 基于数字视差模型和改进SIFT特征的数字近景立体影像匹配[J]. 测绘学报,2012,39(6):624-630.

[14]Yoneyama S,Morimoto Y,Fujigaki M. Phase-Measuring Profilometry of Moving Object without Phase-Shifting Device[J]. Optics and Lasers in Engineering,2003,40(3):153-161.

[15]田铁印,王红,谷凤安,等. 三线阵立体测绘相机光学系统设计[J]. 光学精密工程,2009,17(11):2692-2698.

[16]Lowe,David G. Object Recognition from Local Scale-Invariant Features[C]//Computer Vision,Corfu,Greece,1999:1150-1157.

[17]Lowe,David G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision,2004,60(2):91-110.

[18]李芳芳,肖本林,贾永红,等. SIFT算法优化及其用于遥感影像自动配准[J]. 武汉大学学报(信息科学版),2009,34(10):1245-1249.

[19]汪松. 基于SIFT算法的图像匹配方法研究[D]. 西安:西安电子科技大学,2013.

刘常杰(1973-),男,山东人,副教授,硕士生导师,1996年、1999年、2002年于天津大学分别获得学士、硕士、博士学位,主要从事视觉检测技术方面的研究,liuchangjie@tju.edu.cn;

黄东晓(1987-),男,福建泉州人,硕士研究生,2011年于天津大学获得学士学位,主要从事视觉检测技术方面研究,huangdx89@tju.edu.cn;

杨凌辉(1981-),男,天津人,博士,主要从事激光视觉检测技术及应用研究,icelinker@tju.edu.cn。

ImprovedSIFTAlgorithmBasedonaNewMeasurementSystemofLargeScale3DShape*

LIUChangjie,HUANGDongxiao,YANGLinghui*

(State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China)

The tri-linear CCDs photogrammetry using in surveying was applied to large scale 3-D shape measurement. To pick out the homologous image points from tri-linear CCDs images,SIFT algorithm was used finally. In order to against deficiencies of traditional SIFT,such as time consuming,a new improved SIFT algorithm was proposed. A searching strategy and threshold based on new system were given to meet“real-time”,verified by the experiments. The experiments show that the improved SIFT can cut down the time-consuming and increase the number of matching point-pair and performance of algorithm.

3-D surface measurement;tri-linear CCDs;SIFT;image matching

项目来源:国家863计划项目(2012AA041205)

2014-05-21修改日期:2014-09-11

10.3969/j.issn.1004-1699.2014.11.011

TP391;TH741

:A

:1004-1699(2014)11-1500-06