便携式代谢率检测系统的误差分析及改进*

杨 浩,唐 飞,李曙哲,王晓浩,杨 涛

(1.西南科技大学信息工程学院,四川 绵阳 621010;2.清华大学精密仪器系/精密测试技术及仪器国家重点实验室,北京 100084)



便携式代谢率检测系统的误差分析及改进*

杨 浩1,唐 飞2*,李曙哲2,王晓浩2,杨 涛1

(1.西南科技大学信息工程学院,四川 绵阳 621010;2.清华大学精密仪器系/精密测试技术及仪器国家重点实验室,北京 100084)

通过对便携式代谢率检测系统误差模型进行蒙特卡罗仿真,得到最终误差指标,通过改进测试电路和多传感器数据融合,在非标定条件下实现了仪器的代谢率测试准确度要求。针对温度传感器测试模块进行了误差分析和改进,精度达到0.15 ℃(RMS)。通过极大似然估计对改进电路进行数据融合,保证整个测试过程中温度测试误差在0.124 ℃(RMS)以内,满足了批量生产的高准确度要求,避免了标定过程,降低了生产成本。

代谢率检测;误差统计分析;数据融合;温度传感器

代谢率是指机体生命活动的能量代谢速率,能够反映人体的健康状态,是研究人体能量消耗、需求的重要依据。代谢率的测量可以采用量热法[1]进行气体分析而直接获得结果,或通过经验近似公式来进行间接估算。尽管实际测定代谢率是最准确的,但其测量过程需要在严格的条件下进行,测量仪器昂贵且操作过程复杂,通常采用经验公式估算人体的基础代谢率。Harris-Benedict[2-3]、MifflinStJeor[4]等公式利用人体的身高、体重、年龄等参数,基于统计理论给出了人体的基础代谢率估计,但其不能动态、实时地反映人体的代谢率变化。本文设计了一种便携式代谢率检测仪器,采用多传感器进行实时代谢率测量,并通过改进测试电路和多传感器数据融合,在非标定条件下提高了代谢率测试准确度。

1 便携式代谢率检测原理

根据能量守恒定律,人体代谢产生的能量是储存在体内的热量、对外做功和人体与周围环境的热交换的总和,因此代谢量可用如下公式表达:

M=S+W+H

(1)

其中,M为人体代谢量,S为储存在体内的热量,W为对外做功,H为人体与周围环境的热交换。

在静息状态下,人体对外做功近似为零,储存在体内的热量维持不变,人体代谢产生的能量大部分以热量的形式散发到空气中,用于保持体温的平衡,因此,(1)式可以表示为[5]:

M=H=Qcond+Qconv+Qrad+Ed+Esw+Eres+EL+EP

(2)

其中,Qcond表示着装人体表面与环境的传导换热,Qconv表示着装人体表面与环境的对流换热,Qrad表示着装人体表面与环境的辐射换热,Ed为人体皮肤扩散蒸发热损失,Esw为人体皮肤表面汗液的蒸发热损失,Eres为呼吸潜热损失,EL呼吸显热损失,EP排泄消耗的热损失。

文献[5]给出了式(1)的具体计算方法,可以看出,人体与周围环境的热交换可利用环境温湿度、人体表皮的平均温度和湿润度及人体着装状态进行估算。

因此,在已知人体着装状态的情况下,通过测量环境温湿度、人体表皮的平均温度和湿润度可以估算出人体代谢率。从理论上讲,测量人体表皮的平均温度和湿润度,需要在人体全身各处布置大量的温湿度传感器。这种方式操作复杂,且测试成本较高。

为了实现便携式测试,可以通过检测局部代谢率来估算人体代谢率,而局部代谢率可以通过测量局部(比如指部)温度和湿润度来估算[6]。本文通过计算手指动脉与组织的热交换,并将式(1)中人体代谢率测量方法应用于局部代谢率测量,得到如下公式:

(3)

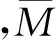
局部动脉血液温度与核心温度有比率关系,而核心温度一般固定不变(37 ℃左右)。因此,除了局部温度和湿润度,为了测量局部代谢率,还需要进行局部血流量检测。局部血流速可通过热传递法来进行测量[7],本文利用贴合在手指表皮的传热棒的远近端温度变化来估算。

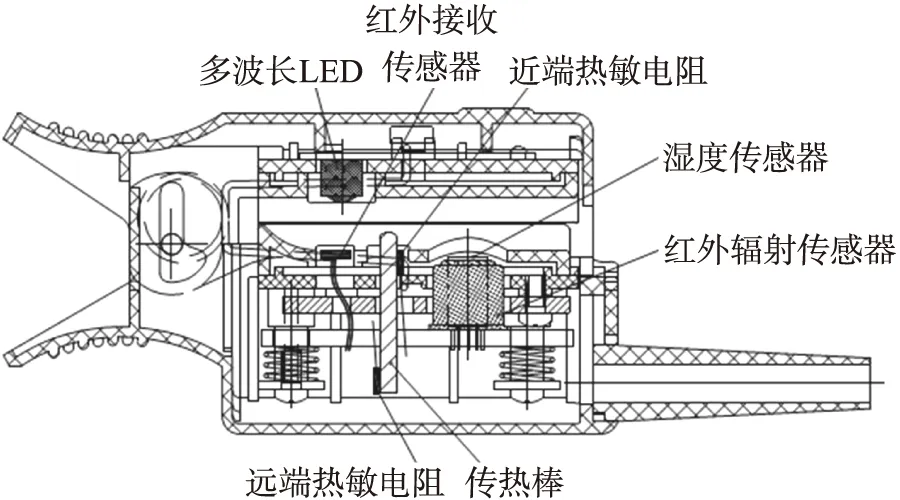
图1 局部代谢率测量探头的结构主视图

图1所示的采集探头通过测量手指的温度和湿润度、环境温湿度来进行局部代谢率测试,所用传热棒一端接触手指皮肤,另一端固定在采集探头的底板上。红外辐射温度传感器采集手指表皮的温度和探头内部温度。以上温度测量点构成了代谢率检测的温度检测系统。

利用式(3)计算代谢率时,可判断1 ℃的温度误差引起的代谢率误差达到10%,因此降低传感器测量误差非常重要。本文以温度测试为实例阐述测试系统的误差分析和多传感器数据融合。

2 温度误差分析及传感器数据融合

2.1 温度测试模块误差分析和改进

每个温度传感模块信号处理需经过传感、放大、滤波、采集完成。假定信号处理中每个信号处理单元的误差都服从独立正态分布,整个传感模块的标准差为:

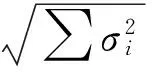
(4)

其中,σi(i=1,…,n)为每个部分的标准差。

为了降低信号处理过程中产生的误差,温度模块的放大、滤波和采集均利用了高精度的IC和精密电阻(0.1%),因此传感部分以外电路中产生的误差较少(不超过0.1 ℃)。经分析可知产生误差最大的部分是传感部分。在测试远近端温度时,将利用高精度的热敏电阻(PT100 A级)和惠斯通电桥来进行温度检测。

图2所示电路是满足小功耗的经典测试电路。在不考虑电桥电阻误差的情况下,由温度变化引起的测量点Vrtj和Vdr之间的电压差可表示为:

(5)

其中,R=R4+R5。此处忽略由温度变化引起的电源电压误差,通过该电压差和温度变化可以得到传感电路的灵敏度。

图2 远近端温度测试电路

Vscale=ΔV(Δt)/ΔtV/℃

(6)

测试温度对应的电压是基准电压测量点Vdr和近端温度传感器分支电压Vrtj之间的电压差,可用如下公式表示:

(7)

实际应用中,不同探头对应的元件特性都有一定程度的差异,而该电路的最终指标和元件之间有式(7)所示的非线性关系,因此难以直接计算出精度特性。本文通过蒙特卡罗模拟方法得出了传感电路温度测试误差特性。从式(7)直接写出蒙特卡罗仿真模型:

(8)

其中～符号表示随机量。

图2的所有元件和供电电压均服从参数为(μ,σ)的正态分布,传感器和元器件的标准差可以参考手册,在特定的环境条件下,产生满足各个元件精度特性的随机数进行蒙特卡罗仿真,仿真的每次随机数发生对应于一个新的探头的元件特性,利用式(8)可以得到每个不同探头远近端温度传感部分输出电压及其标准差。利用式(6)将电压转换成温度之后其标准差为0.21 ℃。考虑放大部分和采集部分标准差(分别为0.08 ℃,0.04 ℃),并利用(1)得出的整个远近端传感模块的标准差为0.23 ℃(3σ为0.69 ℃)。可知允许3σ误差的范围内最大值和最小值差异是1.38 ℃,这将对代谢率测试引起较大的误差。

为了尽量降低传感部分的误差,电桥的所有电阻改成二倍阻值的电阻的并联(前提条件是两个电阻参数独立),在不改变单个电阻精度,同时保持与上述仿真相同的条件下,得到远近端温度传感部分的标准差为0.15 ℃,图3对比了改进前与改进后的电压差分布。

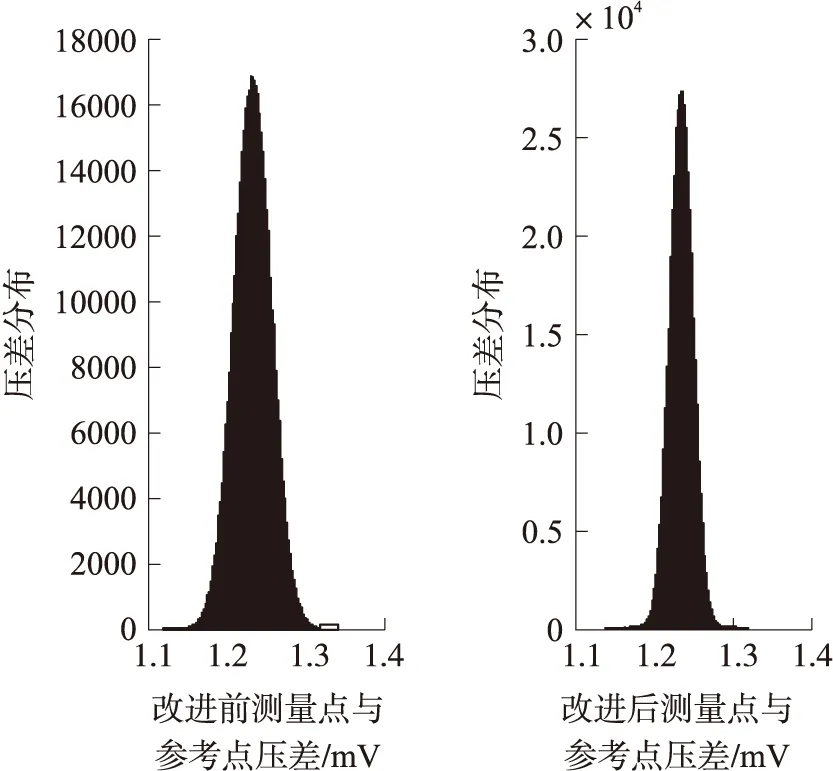
图3 改进前后测量点与参考点的压差分布对比

利用(1)式可以计算整个测试模块的精度(包括放大、滤波、采集)为0.175 ℃(3σ为0.525 ℃)。可以看出改进电路取得了一定效果。

2.2 环境温度融合和传感器校正

即使采用高精度电路设计,并进行了相应的改进,但仍然存在一定的测试误差。

图1中有三个温度传感模块,在整个测量过程中,远、近端温度和探头内部温度的变化过程如图4所示,分别表示为T1(t)、T2(t)、T3(t)。

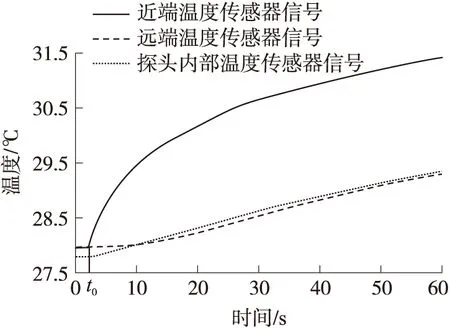
图4 远、近端温度传感器和环境温度传感器的变化

当t=t0时(t0为开始测试时刻),需满足T1(t0)=T2(t0)=T3(t0),而每个传感器都存在误差,实际测试值不可能相等,因此可利用数据融合技术对整个传感器系统进行校正[8]。

温度传感器的测试值可以用下面公式来表达:

T=T0+ΔTc+ΔTt+ΔTn

(9)

其中,T0是真实的温度值,ΔTc、ΔTt、ΔTn分别是常数偏移量、随着温度变化而变化的温度偏移量、随机漂移和随机重复性误差。常数偏移量ΔTt又分为传感器分度表误差和传感器及信号处理电路中产生的误差。

ΔTc=ΔTc1+ΔTc2

(10)

因为本项目应用的是精密信号处理电路,除ΔTc2(对应于3.1中分析的误差)以外,其他误差成分可以控制到最小,所以主要考虑的误差是ΔTc2。

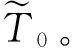
极大似然估计值是通过分析传感器误差(正态分布)得到关于传感器最佳估计值的方法[9]。极大似然函数[10]表示为:

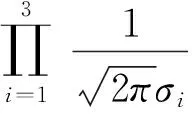
(11)

其中,x1,x2,x3分别代表远、近端温度传感器和环境温度传感器在测试开始时刻的测量值。

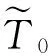
(12)

可以得到关于T0的极大似然估计值为

(13)

在基于置信距离测度的总概率最大值法中[11],设

(14)

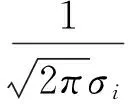
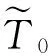
(15)

利用环境温度估计值对每个温度传感器进行偏移量校正,就可以得到校正后的温度变化值。

(16)

3 仿真试验和实验结果

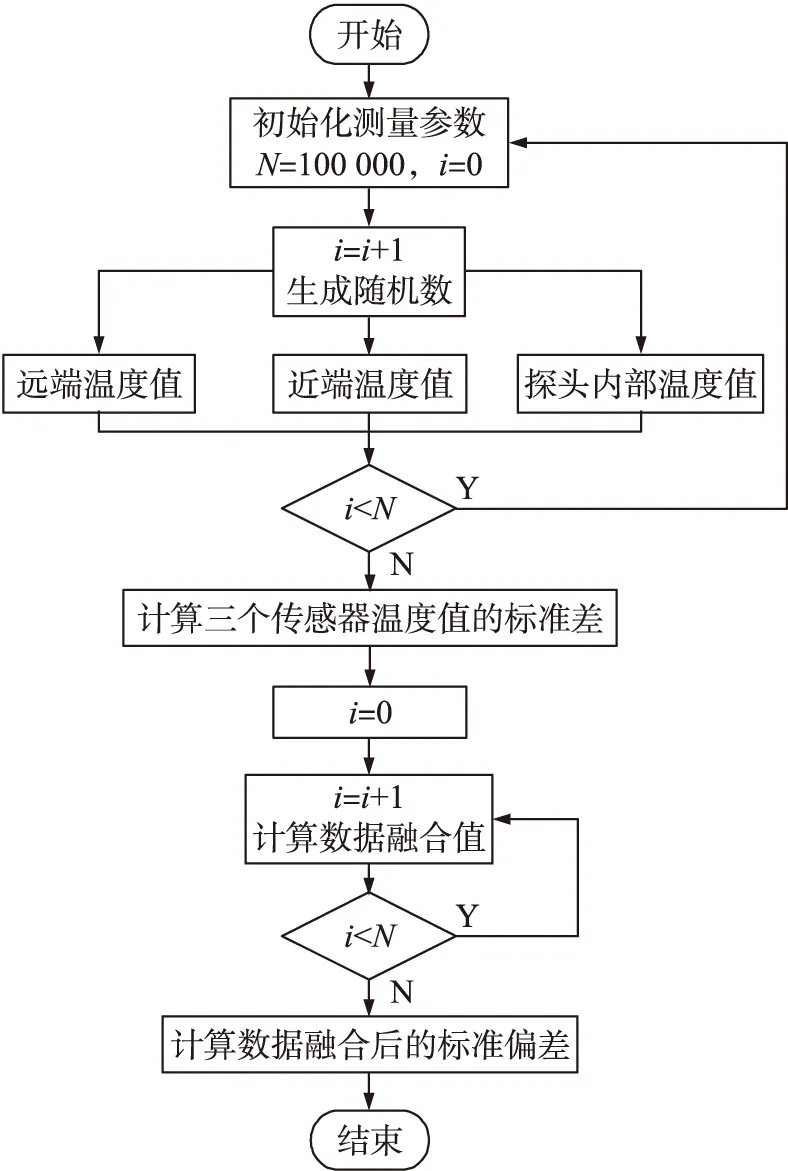
图5 数据处理流程图

整个系统的仿真流程如图5所示。

通过对电路进行改进以及数据融合后[12],当仿真次数N=100 000,真实环境温度T0=23 ℃时,仿真结果如表1所示。

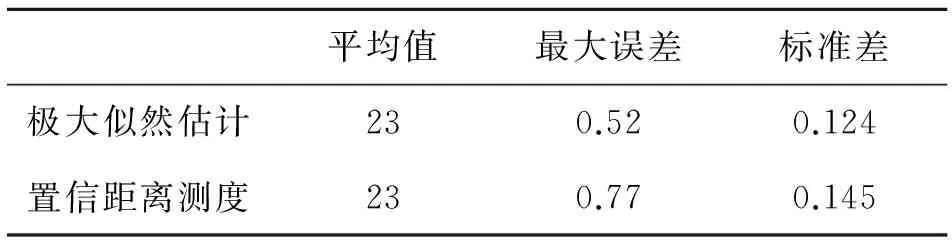
表1 电路改进及数据融合后的仿真结果

利用极大似然估计方法时,得到三个传感器的测量标准偏差从0.175、0.175、0.25降至0.124。利用基于置信距离测度的总概率最大值法时,最终融合结果的标准偏差是0.145,可以看出,在本实验条件下,极大似然法能更好的降低了整个系统的标准偏差。

图6是项目组开发的便携式代谢率测试装置主机和探头。

图6 便携式代谢率测试装置主机和探头

实验过程中,通过在恒温干燥箱中放置一个铁盒,构成双层屏蔽,然后将所有探头放置在铁盒中,并且在干燥箱里温度达到稳定的条件下保持1 h以上,以确保所有探头的环境温度一致。

图7是对10个探头在环境温度为25.1 ℃(利用国家二级标准水银温度计测试的环境温度)时,进行实验得到的远近端温度测试值和环境温度测试值,以及通过最大似然估计得到的融合值。

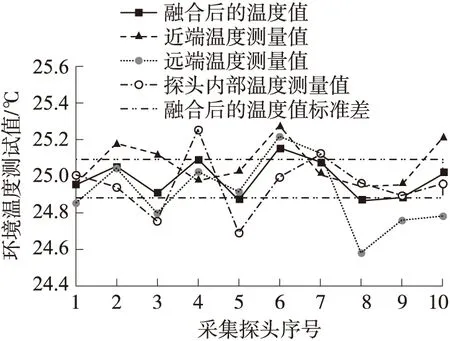
图7 三个传感器及融合后的温度值

从图7中可以看出,对10个探头融合后的数据都在24.8 ℃～25.1 ℃范围内,其标准差为0.12 ℃,且融合后的均值为25.01 ℃,对比真实温度,误差小于0.1 ℃,满足了对温度测量数据的准确性和一致性要求。

通过式(16)对温度值进行校正,得到如图8所示的实际探头中三个传感器的温度值变化过程。可以看出,在整个代谢率检测过程中,远近端温度及探头内部温度均有较好的一致性,可为后续代谢率计算提供准确可靠的温度值。

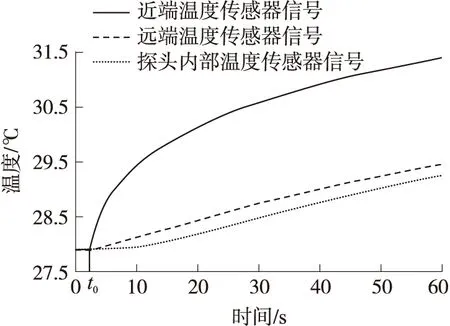
图8 融合及补偿后测试值变化过程

通过仿真及实验,最终确定改进测试电路及数据融合后,温度测试值一致性误差减少了50%。通过式(3)进行代谢率计算,由于传感器测试值的改进,提升了3～5%的代谢率测试准确度。

4 结论

基于电路改进和数据融合,本文提出一种在便携式代谢率检测系统中降低环境温度测量值标准偏差的方法,有效的提升了代谢率测试准确度以及系统的一致性,满足了批量生产的高准确度指标要求,避免了标定过程,降低了生产成本。

[1] Du Charme M B,Kenny G P. A Calorimetric Validation of Evaporative and Dry Heat Losses Measured with Heat Flow Transducers[C]//13th International Conference on Environmental Ergonomics,Boston. 2009.

[2]Roza,Allan M,Shizgal,et al. The Harris Benedict Equation Reevaluated:Resting Energy Requirements and the Body Cell Mass[J]. The American Journal of Clinical Nutrition,1984(40):168-182.

[3]Müller B,Merk S,Bürgi U,et al. Calculating the Basal Metabolic Rate and Severe and Morbid Obesity[J]. Medline,2001(45):1955-1963.

[4]Mifflin M D,St Jeor S T,Hill L A,et al. A New Predictive Equationfor Resting Energy Expenditure in Healthy Individuals[J]. The American Journal of Clinical Nutrition,1990(51):241-247.

[5]刘丽英. 关于着装人体热舒适方程的计算与分析[J]. 青岛大学学报,2013,28(4):68-70.

[6]唐飞,王晓浩,王东生,等. 代谢热整合法无创血糖检测技术研究[J]. 仪器仪表学报,2007(10):1858-1859.

[7]李俊峰,唐飞,徐效文,等. 热传递法无创测量血液流速[J]. 仪器仪表学报,2006(6):1178-1180.

[8]黄漫国,樊尚春,郑德智,等. 多传感器数据融合技术研究进展[J]. 传感器与微系统,2010,29(3):5-8.

[9]周逸峰,亨利·伦帕特,瑞克·C·亚普. 数据融合的精确极大似然配准算法[J]. 情报指挥控制系统与仿真技术,1998(6):20-40.

[10]陈福增. 多传感器数据融合的数学方法[J]. 数学的实践和认识,1995(2):11-16.

[11]于耀亮,姜嘉言,张立明. 一种新的距离测度学习算法[J]. 信息与电子工程,2008,6(4):115-119.

[12]段宗涛,程豪,康军. 基于数据融合的多传感器实时数据处理系统[J]. 电子设计工程,2014,22(7):43-46.

杨浩(1989-),男,硕士研究生。研究方向为移动智能系统,智能医疗仪器;.

唐飞(1973-),男,副教授,硕士生导师。主要研究方向为精密测量和控制技术、微系统设计和工艺等,tangf@mail.tsinghua.edu.cn。

TheErrorAnalysisandImprovementofPortableMetabolicRateDetectionSystem*

YANGHao1,TANGFei2*,LIShuzhe2,WANGXiaohao2,YANGTao1

(1.School of Information Engineering,Southwest University of Science and Technology,Mianyang Sichuan 621010,China;2.State Key Laboratory of Precision Measurement Technology and Instruments,Department of Precision Instrument,Tsinghua University,Beijing 100084,China)

In this paper,utilizing Monte Carlo simulation on the error model of portable metabolic rate detection system,obtained the final error indicators. Improved test circuit and used multi-sensor data fusion to achieve metabolic rate test instrument accuracy requirements in non-calibrated conditions. Through sensor error analysis and improvement,the accuracy of temperature test module of the project reached 0.15 ℃(RMS). In addition,through the maximum likelihood estimate of the improvement circuit for data fusion,it can ensure that the test error is 0.124 ℃(RMS)or less throughout the temperature testing process,meet the requirements of high accuracy of mass index,avoided the calibration process,reduced the cost of production.

metabolic rate detection;error statistical analysis;data fusion;temperature sensor

项目来源:国家863项目(2011AA040406)

2014-08-20修改日期:2014-09-10

10.3969/j.issn.1004-1699.2014.11.009

TP393

:A

:1004-1699(2014)11-1490-05