无线传感器网络中一种新的无条件安全密钥协商模型*

王秋华,吕秋云,王小军,骆 懿,游 林

(杭州电子科技大学通信工程学院,杭州 310018)



无线传感器网络中一种新的无条件安全密钥协商模型*

王秋华*,吕秋云,王小军,骆 懿,游 林

(杭州电子科技大学通信工程学院,杭州 310018)

针对现有无条件安全密钥协商模型中存在的问题,提出了一种获取初始随机相关信息的新模型。实验结果表明,与现有模型相比,新模型和原信源模型和原信道模型在功能上等价,但新模型在保证合法通信双方之间的误比特率不变的情况下,增加了窃听方的误比特率,弱化了窃听方的优势,提高了密钥协商的总信息率。

无线传感器网络;无条件安全;密钥协商

安全性问题是制约无线传感器网络WSN(Wireless Sensor Networks)发展的重要难题[1],目前,该问题主要采用加密和认证技术来解决,其核心是密钥的安全分配与协商。由于传感器节点在计算能力、存储空间及电源能力上受限,基于预分配的密钥管理方案或ECC加密算法是WSN主要采用的安全措施。但现有的密码体制(私钥和公钥密码体制)是建立在计算安全模型之上的[2],随着算法效率和计算机计算能力的提高(如量子计算机),基于计算安全的密码体制越来越受到威胁,时刻面临被攻破的危险,必然刺激我们去研究具有无条件安全的密码体制。

无条件安全模型以信息论为基础,假定敌手有无限的资源和能力,即使他能够在很短时间内遍历所有密钥,也不能攻破基于信息论的安全体系。无条件安全得以实现的关键是无条件安全密钥协商协议的设计,只要通信双方能共享一个无条件安全的密钥,就能利用一次一密密码体制,加密双方的通信内容,最终实现无条件安全的保密通信[3]。

无条件安全密钥协商是在不事先共享密钥的情况下,产生源源不断的共享密钥的机制[4],是近几年研究的一个热点。它建立在无条件安全模型之上,在具有强大计算能力的量子计算机面前仍然能提供绝对安全的秘密通信。无条件安全的密钥协商机制既可作为现有安全机制的补充,也适应未来安全技术的发展需求。

相比于传统的WSN密钥分配和加密方式,无条件安全的密钥协商具有更强的安全性,且需要更少的节点存储空间,例如,通过无条件安全协商出的112bit的密钥在加密强度上相当于2 048 bit Diffie-hellman密钥[4],另外,无条件安全的密钥协商比传统的加密方式需要更少的计算复杂度[5]。更重要的是,无条件安全的密钥协商在初始化阶段需要通过无线有扰信道传输方式获取初始相关信息,有些模型甚至要求进行密钥协商的节点间要直接进行无线信号的收发,而无需基站等其它设施的中转,而此机制正好符合WSN的无线通信机制,故无条件安全的密钥协商在WSN中具有更强的应用优势。

无条件安全密钥协商的基本思想是:首先,合法通信双方获得初始随机相关信息,然后,利用该初始相关信息,通过无条件安全密钥协商协议,获得源源不断的密钥流,进而实现完善保密通信。

假定通信的发方是Alice,收方是Bob,Eve为窃听方,无条件安全密钥协商过程可以抽象为:

①初始化阶段:该阶段是原始密钥的获取阶段。Alice,Bob和Eve分别得到3个相关随机变量X,Y和Z作为他们各自的初始密钥信息,X,Y和Z服从联合概率分布pXYZ。

②通信阶段:得到初始随机相关信息后,利用密钥协商协议,Alice和Bob通过公开信道交换信息,产生最终密钥,这一过程也称为公开讨论(public discussion),具体分为优先提取[7-8],信息协调[9-10]和保密增强[11-12]3个阶段。(a)优先提取:如果Eve接收信道的误比特率小于合法接收者的,合法通信双方的互信息将小于窃听方与发方之间的,优先提取就是把Alice与Bob间相对于Alice与Eve间的互信息由劣势转化为优势的过程。优先提取后,相对于Eve,Bob拥有更多的关于Alice的比特串的信息。(b)信息协调:优先提取执行后,Bob与Alice间的比特串并不完全相同,还需要信息协调过程,纠正通信双方比特串中不一致的比特。去除Bob和Alice优先提取后不一致比特的过程即为信息协调。(c)保密增强:密钥协商的最后一个阶段是保密增强,合法通信双方从一个部分保密的比特串中,提取一个高度保密比特串的过程称为保密增强。

③决策阶段:如果Alice和Bob认为最终协商出的密钥K可以作为他们之间的共享密钥,则接受,否则,删除K,重新进行密钥协商。

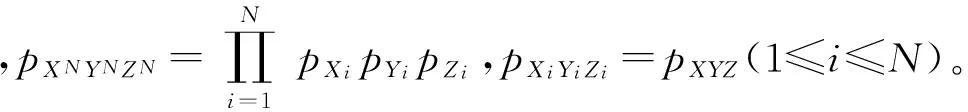
定义1在随机变量Z条件下的随机变量X,Y的密钥速率,由S(X;Y||Z)表示,定义为在使Eve获得信息速率任意小的情况下,Alice和Bob能够协商一个密钥K的最大速率,即对任意ε>0,分别用X和Y代替XN和YN,则当N充分大时,总存在一个密钥协商协议,使满足

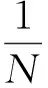
(1)

和

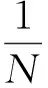
(2)

的协商密钥速率R达到最大。

定理1在随机变量Z条件下,随机变量X,Y的密钥速率的上界为

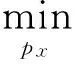
(3)

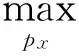
(4)

在文献[6]中,Maurer证明:如果通信双方的初始信息毫不相关,则无条件安全密钥协商的速率为零,即无条件安全的密钥协商不可能实现。因此,在信息理论安全的密钥协商中,总有一个初始化阶段产生通信双方的初始相关信息,而如何得到该初始随机相关信息成为研究的重点。目前的方法主要是基于量子信道传输[13]或无线有扰信道传输[6,14],但由于量子信道传输距离短,价格昂贵,因此现有的密钥协商方案大都以有扰信道模型为基础进行设计的。在无线网络中,目前利用信道噪声产生随机相关信息的方式主要有一般信源模型Model SW(Source-Type Model with Wiretapper)和一般信道模型Model CW(Channel-Type Model with Wiretapper)。

本文主要研究了无条件安全密钥协商模型,首先分析了在初始化阶段产生随机相关信息的模型Model SW和Model CW及其存在的主要问题;然后在此基础上,提出了一种WSN中获取初始随机相关信息的新模型,并对新模型和原有模型进行了分析与比较。

1 无条件安全密钥协商模型

1.1 Model SW

在图1所示的信源模型Model SW中[15],假设存在一个随机信号源,通过各自有噪声的信道,通信双方对随机信号源进行观测,然后,在一个公开无差错信道上协商如何利用观察到的随机数据生成密钥。目前公认较为实际的是Maurer提出的以卫星广播信号作为随机信源的模型[6]。在该模型中,卫星以低信噪比不断向地面发送随机比特串U=(u1,u2,…,uN)∈{0,1}N,Alice,Bob和Eve分别通过无记忆二进制对称信道BSC(Binary Symmetric Channels)以误比特率pA,pB和pE得到3个随机比特串X=(x1,x2,…,xN)∈{0,1}N,Y=(y1,y2,…,yN)∈{0,1}N,和Z=(z1,z2,…,zN)∈{0,1}N作为初始信息,其中,pA=Pr{xi≠ui},pB=Pr{yi≠ui},pE=Pr{zi≠ui}。X,Y及Z服从联合概率分布pXYZ。

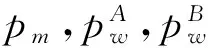
pm=pA+pB-2pApB

(5)

(6)

(7)

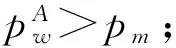
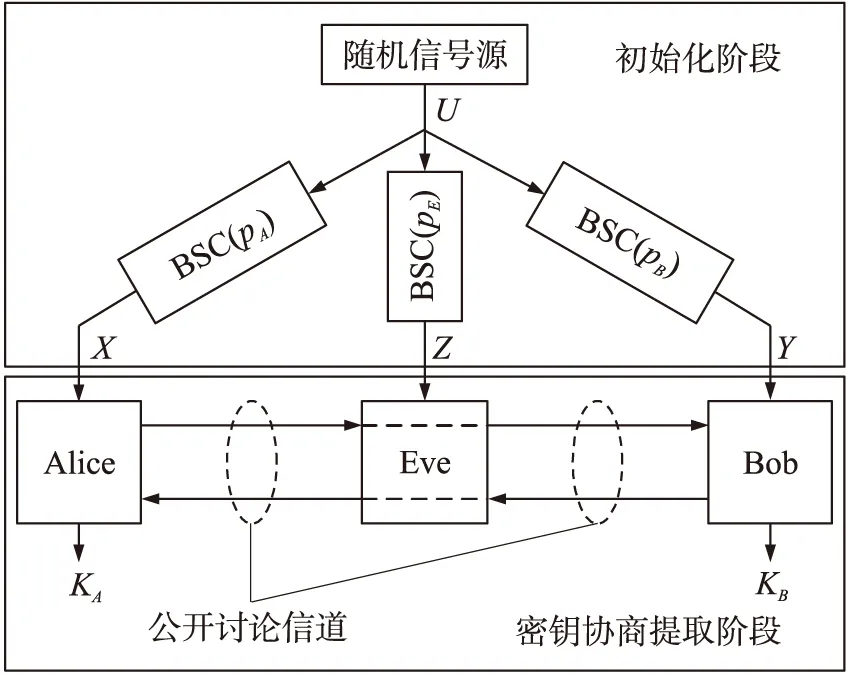
图1 Model SW

定理3令随机变量X,Y,Z是根据p(ui=0)=p(ui=1)=0.5,PXYZ|U=pApBpE的规则产生的,则密钥协商速率的下界为

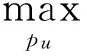
(8)

其中,h(p)=-plog2(p)-(1-p)log2(1-p)。

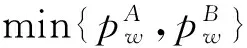
1.2ModelCW

在图2所示的信道模型Model CW中[16],Alice产生随机序列X=(x1,x2,…,xN),并通过条件概率分布为pY|X的离散无记忆信道(Discrete Memoryless Channel,DMC){W:Alice(Bob×Eve}传输给Bob。由于信道中存在噪声,Bob收到X的噪声版本Y=(y1,y2,…,yN),而Eve通过一个不同的信道(由概率pZ|X表征)接收到X的噪声版本Z=(z1,z2,…,zN)。然后,Alice和Bob通过一个公开无差错信道协商如何利用X和Y产生共享密钥,而Eve却不能获得此密钥。

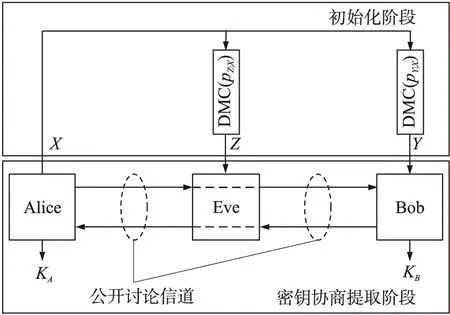
图2 Model CW

定理4假设Bob和Eve的接收信道是相互独立的二元对称信道,其误比特率分别为ε和δ,则密钥协商速率的下界为

(9)

式(9)表明,只有当ε<δ,即Bob的接收信道好于Eve的接收信道时,Bob与Alice才可以进行密钥协商。

在后续讨论中,我们均以Alice的比特串为基准进行密钥协商。

1.3 存在问题分析

合法双方可以通过公开协商,在他们接收数据基础上产生共享密钥,而决定密钥保密性的关键是噪声信道输出的信息差异与没有信道能够完全保证无差错。在Model SW和Model CW中,通信双方获取初始相关信息方法的本质是利用信道中的噪声增加窃听方对信息的不确定性。

对于Model SW,目前公认较为实际的是卫星广播模型,但该模型存在以下两个问题[17]:①接收双方的同步问题;②需要额外配备卫星信号接收装置,增加成本,而且并不是任何企业或个人都可以通过卫星的噪声信道获得初始比特串(原始密钥)。

对Model CW,当Eve接收信道的误比特率小于Bob接收信道的误比特率时,需要执行优先提取协议把Alice和Bob之间的互信息由劣势转为优势。但通过分析可知,比特对优先提取协议仅降低合法通信双方的误比特率,而窃听方的误比特率保持不变。且当Eve接收信道的误比特率较小时,在信息协调阶段,借助于合法方在公开信道上交换的信息,Eve的误比特率会进一步下降,使其后续保密增强阶段提取密钥的信息率进一步降低,导致密钥协商的总信息率非常低。例如,在信道模型中,当ε=0.1,δ=0.05时,需要进行1轮比特对优先提取协议和2轮Winnow信息协调协议。一轮比特对优先提取协议的信息率为41%,2轮winnow信息协调协议的信息率为73.41%,保密增强协议的信息率为12.53%,则密钥协商协议的信息率仅为3.77%。

同时,通过定理3和定理4,在Model SW和Model CW中,当Eve接收信道的误比特率比Bob的小时,密钥协商的速率为0。虽然可以通过后续的优先提取协议,使得I(X;Y)>I(X;Z)和I(X;Y)>I(Y;Z),但通过分析可知,优先提取协议的执行大大降低了密钥协商协议的速率和整个密钥协商协议的总信息率;另一方面,当Eve接收信道的误比特率较小时,保密增强阶段提取密钥的信息率很低,甚至无法提取安全的密钥。比特对优先提取协议不能降低窃听方的误比特率,而Winnow协议却使Eve的误比特率进一步降低,从而导致后续保密增强协议失效。所以,我们应当在初始化阶段就尽量增大比特串对(X,Z)之间的误比特率,这样才能保证后续密钥协商各阶段的有效执行。基于以上考虑,我们提出了一种适用于WSN的新的密钥协商模型。

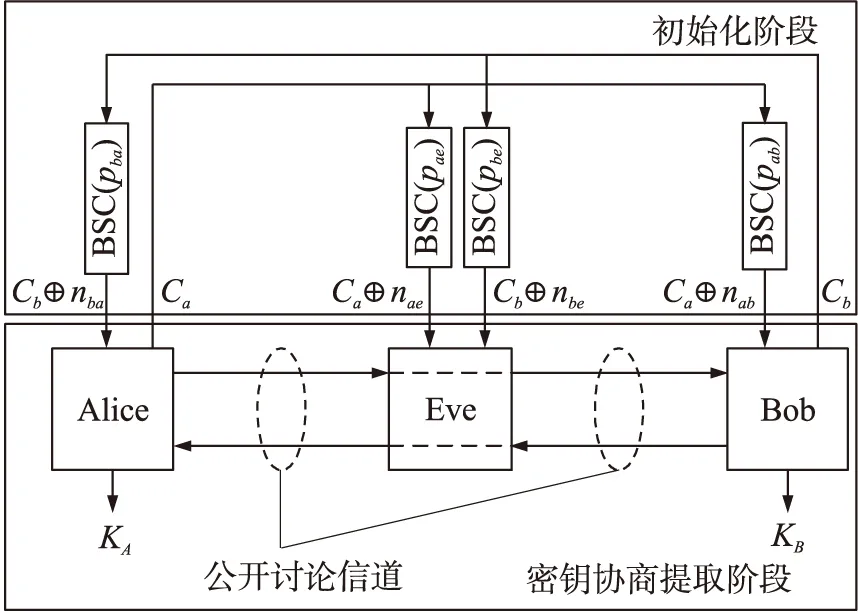
图3 新模型

2 一种新的密钥协商模型

2.1 模型描述

新模型如图3所示。具体实现步骤如下:

①Alice随机产生比特串Ca,并通过BSC广播信道以低信噪比发送给Bob,Bob接收到的是Ca的衰落版本Ca⊕nab,nab为噪声比特串,且p(nab=1)=pab;此外,Eve也接收到Ca的衰落版本Ca⊕nae,nae为噪声比特串,且p(nae=1)=pae;

②同样,Bob随机产生比特串Cb,并通过独立的BSC广播信道以低信噪比发送给Alice,Alice接收到的是Cb的衰落版本Cb⊕nba,nba为噪声比特串,且p(nba=1)=pba;此外,Eve也接收到Cb的衰落版本Cb⊕nbe,nbe为噪声比特串,且p(nbe=1)=pbe;

③Alice计算X=Ca⊕Cb⊕nba,Bob计算Y=Ca⊕Cb⊕nab,为他们的初始相关信息;Eve只能获取比特串Z=Ca⊕Cb⊕nae⊕nbe。

在后续的通信阶段,Alice和Bob通过一个公开无差错信道来协商如何利用X和Y产生共享密钥,且使Eve不能得到此密钥。

2.2 模型分析与比较

新模型中,通信双方节点直接通过无线收发方式获取初始相关信息,符合WSN的通信机制。

在新模型中,Bob的初始比特串Y=Ca⊕Cb⊕nab相对于Alice的初始比特串X=Ca⊕Cb⊕nba的误比特率为:

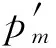
=Pr{nab≠nba}=pab+pba-2pabpba

(10)

Eve初始比特串Z=Ca⊕Cb⊕nae⊕nbe相对于Alice的初始比特串X=Ca⊕Cb⊕nba的误比特率为:

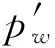
=Pr{nae⊕nbe≠nba}=Pr{nae⊕nbe⊕nba=1}

=pba+(pae+pbe-2paepbe)-2pba(pae+pbe-

2paepbe)=pba+pe-2pbape

(11)

其中,pe=pae+pbe-2paepbe。

若把新模型中的数据用卫星模型进行实现,则可做如下设置。

卫星广播初始比特串U=Ca⊕Cb,Alice,Bob和Eve分别通过误比特率为pA,pB和pE的信道进行接收,各自得到U的衰落版本X=Ca⊕Cb⊕nA,Y=Ca⊕Cb⊕nB和Z=Ca⊕Cb⊕nE。其中,nA,nB,nE分别为Alice,Bob和Eve收到的噪声比特串,且p(nA=1)=pA,p(nB=1)=pB,p(nE=1)=pE。

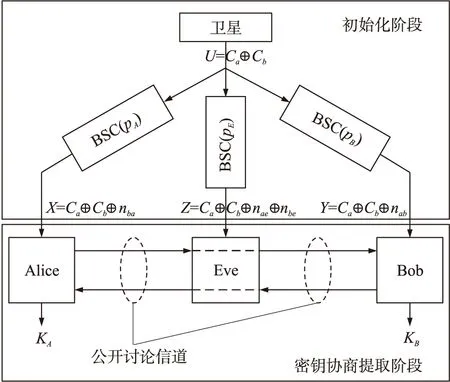
图4 新模型与卫星广播模型的等价性

如果假设pA=pba,pB=pab,pE=pae+pbe-2paepbe,则nA=nba,nB=nab,nE=nae⊕nbe,此时,新模型和卫星广播模型在功能上等价,等价模型如图4所示。

但是,在新模型中,通信的传感节点无需额外卫星信号接收硬件装置,节约了成本。Alice和Bob获取到初始相关比特串后,可以利用优先提取、信息协调和保密增强协商他们的共享密钥。容易看出,与原卫星模型相比,新模型在保证Alice和Bob间误比特率不变的情况下,增加了Eve和Alice间的误比特率,有助于提高协议的总信息率。

同样,若把新模型中的数据用Model CW模型实现,则可做如下设置:

Alice发送比特串X=Ca⊕Cb⊕nba,Bob和Eve分别通过误比特率分别为ε和δ的信道接收到X的衰落版本Y=(Ca⊕Cb⊕nba)⊕nAB,Z=(Ca⊕Cb⊕nba)⊕nAE。其中,nAB,nAE分别为Bob和Eve收到的噪声比特串,且p(nAB=1)=ε,p(nAE=1)=δ。

如果假设ε=pba+pab-2pbapab,δ=pba+(pae+pbe-2paepbe)-2pba(pae+pbe-2paepbe),则nAB=nab⊕nba,nAE=nae⊕nbe⊕nba,此时,新模型与Model CW模型在功能上也等价。

由于新模型增大了比特对(X,Z)间的误比特率,弱化了Eve的优势,提高了密钥协商的总信息率。由定理4得出,若以Alice得到的比特串为基准进行密钥协商,则新模型密钥协商理论速率的下界为:

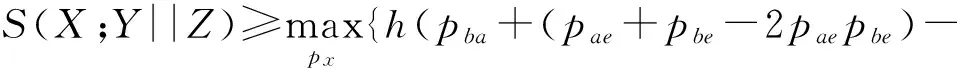
2pba(pae+pbe-2paepbe))-

h(pab+pba-2pabpba)}

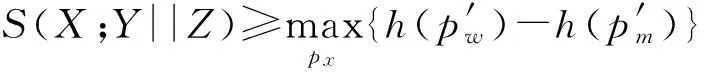
(12)

为比较方便,假设3种模型下的信道误比特率为:pA=pB=ε=pab=pba=p,pE=δ=pae=pbe=q。表1列出了新模型与Model SW、Model CW的密钥协商理论速率的比较值,由表1可以看出,在相同条件下,新模型提高了密钥协商的理论速率,且使合法方之间的误比特率的适应范围增大。

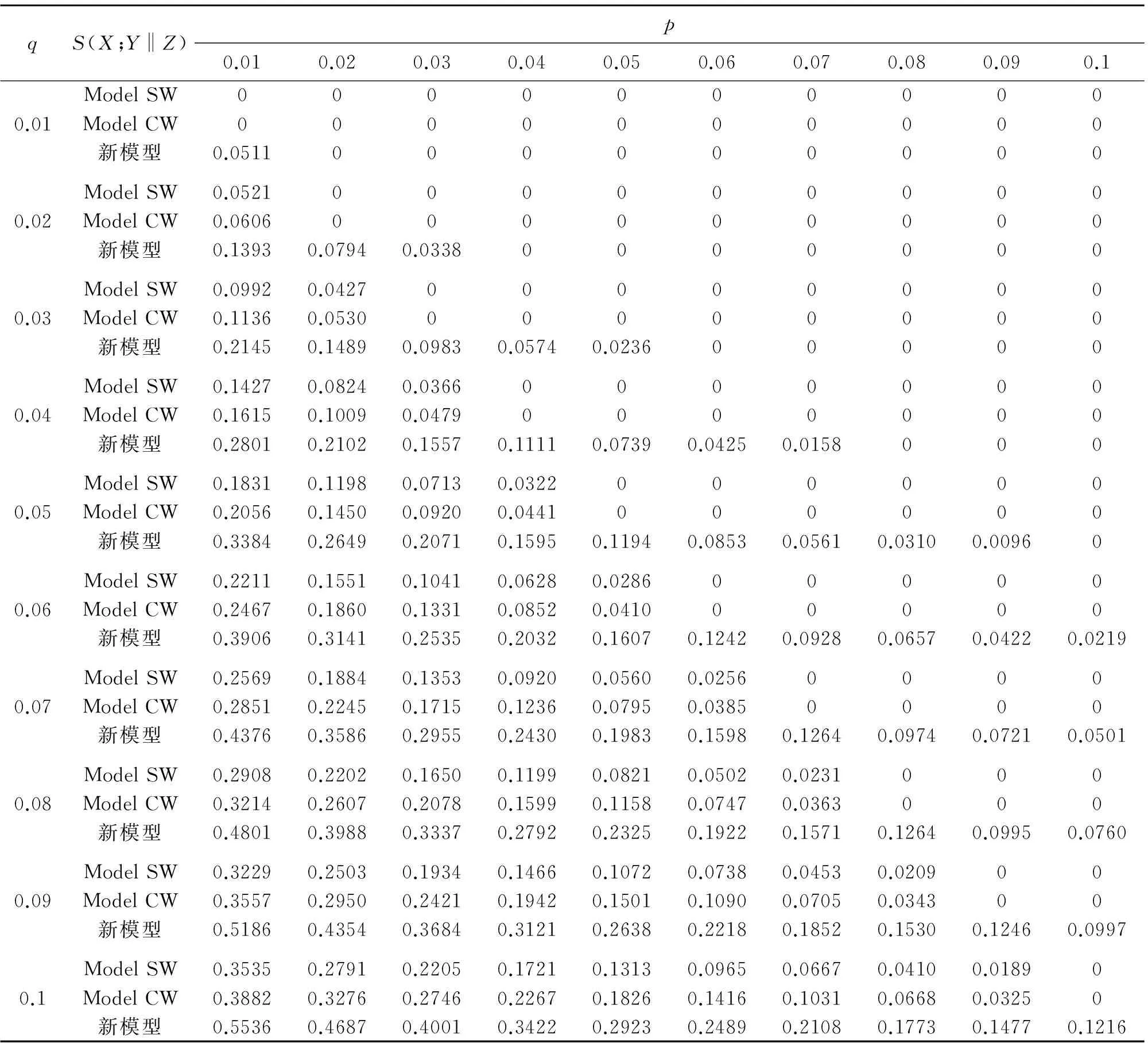
表1 新模型与Model SW、Model CW的密钥协商理论速率比较

3 实验结果

3.1 实验环境设置

除了上述理论分析,我们进一步在实际WSN环境下对上述3种模型进行了性能比较。试验中的随机数采用SK-WSN-43实验系统CC2530自带的随机数发生器芯片产生。

新模型:首先节点Alice产生初始随机比特串Ca,并通过广播方式以低信噪比发送给Bob,Bob接收到Ca的衰落版本Ca⊕nab后即把自己产生的随机比特串Cb通过广播方式以低信噪比发送给Alice,Alice接收到的是Cb的衰落版本Cb⊕nba,窃听节点Eve接收到Ca的衰落版本Ca⊕nae,和Cb的衰落版本Cb⊕nbe。

实验过程中,设置其它传感器节点无序并发信息,对Alice和Bob间的通信形成干扰。

Model SW:为了和Model SW做比较,我们利用WSN基站作为随机信源模拟卫星场景,取Alice和Bob在新模型试验中产生的随机比特串的异或结果,即Ca⊕Cb作为基站广播信号,该信号分别由Alice、Bob和Eve接收。

Model CW:为了和Model CW做比较,我们设置实验场景如下:Alice把在新模型实验中计算得到的随机比特串X=Ca⊕Cb⊕nba进行广播,Bob和Eve分别进行接收。

同时,在试验中,为了有效克服WSN中存在的同频串扰问题,本文采用了S-MAC协议[18],采用虚拟载波侦听和物理载波侦听,以及请求发送/清除发送(RTS/CTS)交换技术,使与此次通信无关的节点进入休眠状态,以减少串扰带来的能量损耗,提升协议的执行效率。

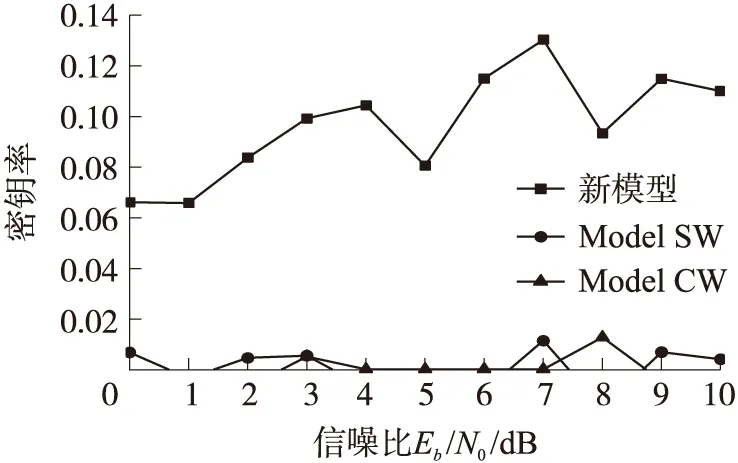
图5 新模型与Model SW、Model CW的密钥率比较

3.2 实验结果

图5为在3种模型实验环境下所测得的实验结果,由图5可以看出,在相同的信噪比环境中,新模型下的密钥率远高于Model SW和Model CW,这是因为新模型增加了Eve和Alice间的误比特率,弱化了Eve的优势。

4 结论

针对现有无条件安全密钥协商初始化模型中存在的问题,提出了WSN中一种新的密钥协商模型。在新模型中,通信双方无需额外的卫星信号接收硬件装置,节约了成本。Alice和Bob获取到初始相关比特串后,即可以利用优先提取、信息协调和保密增强协议协商他们的共享密钥。与现有模型相比,新模型在保证Alice和Bob间误比特率不变的情况下,增加了Eve和Alice间的误比特率,弱化了Eve的优势,有助于提高后续协议的总信息率。新模型的性能优势在实际实验环境中得到进一步的验证。

今后,如何在新模型的基础上设计适应WSN的效率更高的优先提取、信息协调和保密增强协议是作者进一步研究的重点。

致谢

本文由浙江省数据存储传输及应用技术研究重点实验室(杭州电子科技大学)资助。

[1] 王秋华,陈惠芳,谢磊,等.无线传感器网络一种改进的随机密钥预分配方案[J].传感技术学报,2010,23(10):1494-1500.

[2]Rivest R L,Shamir A,Adleman L.Method for Obtaining Digital Signatures and Public-Key Cryptosystems[J].Communications of the ACM,1978,21(2):120-126.

[3]秦兴成.信息理论安全密钥协商的研究[D].西安:西安电子科技大学,2003.

[4]Lenstra A K,Verheul E R.Selecting Cryptographic Key Sizes[J].Journal of Cryptology,2001,14(4):255-293.

[5]Jessica Erin Dudley Croft.Shared Secret Key Establishment Using Wireless Channel Measurements[D].A Dissertation Submitted to the Faculty of The University of Utah in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy,2011:7.

[6]Maurer U M.Secret Key Agreement by Public Discussion from Common Information[J].IEEE Transactions on Information Theory,1993,39(3):733-742.

[7]Maurer U M.Protocols for Secret Key Agreement Based on Common Information.Advances in Cryptology-CRYPTO’92[J].Lecture Notes in Computer Science,1993,740:461-470.

[8]Liu S,Henk C A,Tilborg V,et al.A Practical Protocol for Advantage Distillation and Information Reconciliation[J].Designs,Codes and Cryptography,2003,30:39-62.

[9]Yan H,Ren T,Peng X,et al.Information reconciliation Protocol in Quantum Key Distribution System[C]//Proc of the 4th Int Conf on Natural Computation(ICNC’08),2008.

[10]Buttler W T,Lamoreaux S K,Torgerson J R.Fast,Efficient Error Reconciliation for Quantum Cryptography[J].Phys Rev A,2003,67:052303.

[11]Bennett C.Quantum Cryptography Using Two Nonorthogonal States[J].Phys Rev Lett,1992,68:3121-3124.

[12]Ahlswede R,Csiszár I.Common Randomness in Information Theory and Cryptography—partⅠ:Secret Sharing,IEEE Transactions on Information Theory[J].1993,39(4):1121-1132.

[13]Maurer U,Wolf S.Privacy Amplification Secure Against Active Adversaries,Advances in Cryptology-CRYPTO’97[J].Lecture Notes in Computer Science,1997,1294:307-321.

[14]Watanabe Y.Privacy Amplification for Quantum Key Distribution[J].Journal of Physics A:Mathematical and Theoretical,2007,40(3):99-104.

[15]Yakovlev V,Korzhik V,Morales-Luna G,et al.Key Distribution Protocols Based on Extractors Under the Condition of Noisy Channels in the Presence of an Active Adversary,2010,arXiv:1005.3184[cs.IT].

[16]Ahlswede R,Csiszár I.Common Randomness in Information Theory and Cryptography—PartⅠ:Secret Sharing[J].IEEE Transactions on Information Theory,1993,39(4):1121-1132.

[17]王保仓.基于有扰认证信道的信息理论安全密钥协商[D].西安:西安电子科技大学,2004.

[18]Ye W,Heidemann J,Estrin D.Medium Access Control with Coordinated Adaptive Sleeping for Wireless Sensor Network[J].IEEE ACM Transactions on Networking,2004,12(3):493-506.

王秋华(1978-),女,博士,杭州电子科技大学教师,研究方向为传感器网络安全、计算机网络安全、安全密钥管理等,wangqiuhua@hdu.edu.cn。

ANewUnconditionallySecureSecretKeyAgreementModelforWirelessSensorNetworks*

WANGQiuhua*,LvQiuyun,WANGXiaojun,LUOYi,YOULin

(School of Communication Engineering,Hangzhou Dianzi University,Hangzhou 310018,China)

To resolve the problems in the unconditionally secure secret key agreement model,a new model to obtain the initial random related information was proposed.The experiment results show that compared with existing models,the new model is equivalent in function to the source model and the channel model.However,in the new model,the bit error rate between legal communication parties remains unchanged,while the bit error rate of eavesdropper increases.Hence,the advantage of eavesdropper weakens and the total information key agreement rate increases.

wireless sensor networks(WSN);unconditionally secure;secret key agreement

项目来源:浙江省自然科学基金青年基金项目(LQ14F020010);国家自然科学基金项目(61272045);浙江省杭电智慧城市研究中心项目

2013-11-06修改日期:2014-06-03

10.3969/j.issn.1004-1699.2014.06.021

TP393.08

:A

:1004-1699(2014)06-0821-07