数控转塔冲床机身动态特性分析
邹 瑶,汤文成
(东南大学 机械工程学院,江苏 南京 211189)
数控转塔冲床机身动态特性分析
邹 瑶,汤文成
(东南大学 机械工程学院,江苏 南京 211189)
为了研究数控转塔冲床机身的振动情况,以江苏亚威机床股份有限公司的HPR-3048数控转塔冲床为例,对机床机身进行有限元模态分析和实验模态分析,建立准确的有限元模型,同时通过塑性成形软件DEFORM计算板料冲孔时模具冲裁力的时间历程曲线,并以此作为动态载荷,通过模态叠加法计算机床的动态响应,得出机身冲裁过程中的最大动应力、最大动态位移以及几个关键点动态位移的时间历程曲线和模态参与因子随时间变化的三维曲面,为减小机床的振动提供实际指导。
数控转塔冲床;有限元模态分析;实验模态分析;冲裁工艺;瞬态分析
数控转塔冲床是一种柔性薄板冲压加工设备,发展至今已有70多年历史,随着工业生产的需要,其冲压速度和冲压吨位不断提高,传统的静态设计已经不能满足实际的设计需求,其设计已经进入动态设计阶段[1]。本文利用实验法和有限元法建立了准确的有限元模型,通过数值模拟计算得到了冲裁工艺的模具冲裁力时间历程曲线,研究了冲床机身在循环周期冲击力作用下的动态响应,找出了机身的薄弱部位,为冲床的结构优化提供指导。
1 有限元模型的建立
数控转塔冲床机身主要是由Q235-A型钢板焊接而成,除了主板上的加强筋之外,其他钢板的厚度相对于其长宽来说比较小,根据经典板壳理论,当板的厚度t与板最小边长a的比,即t/a≤1/5时可以认为该板是薄板[2]。因而本文对于冲床机身各钢板采用壳单元来进行离散,而对于主板上的加强筋则采用实体单元进行建模。至于冲床中大量的焊缝,采用SEAM连接方式中的CWELD焊接单元来模拟。图1为冲床机身的有限元模型,共划分了373 018个壳单元和21 690个实体单元。
2 模态分析
模态分析是结构动力学分析的基础,其主要目的是得到结构的一些固有特性,比如模态频率、模态振型、模态阻尼等,同时可以根据机床的固有频率来避开冲床的工作频率,以避免共振,减小振动[3],而且通过实验模态分析与有限元模态分析结果的对比,可以对有限元模型进行修正,建立准确的有限元模型。另外本文的瞬态分析采用的是基于模态叠加法,所以在动态响应分析之前进行模态分析是非常必要的。

图1 冲床机身有限元模型
冲床有限元自由模态分析和实验模态分析前四阶非刚体模态的频率以及主振型(自由模态前六阶为刚体模态)如图2所示。
由分析结果对比可知,有限元分析的结果和实验结果的最大误差为15.24%,在误差允许范围之内,说明有限元模型具有一定的准确性。由图2可知,数控转塔冲床机身的一阶振型主要是主板上方左右主墙板在Z方向的同向一阶弯曲振动以及工作台板在Y方向的一阶上下振动;二阶振型主要是主板上方左右主墙板在Z方向的反向弯曲振动;三阶振型主要是主板上方左右主墙板在Z方向的同向二阶弯曲振动;四阶振型主要是主板上方左右主墙板在Z方向的同向三阶弯曲振动以及工作台板在Y方向的二阶上下振动。左右墙板Z方向的振动将导致冲头在Z方向的移动,造成定位精度的降低,同时导致加工孔的圆柱度降低;工作台板Y方向的振动将导致胚料钢板的振动,影响胚料的定位以及加工精度,所以相对于整机来说,主板上方左右主墙板和工作台板的刚度相对较弱,同时也是对加工精度影响较大的两个部位,这两个部位需要给予一定程度的加强。

图2 冲床有限元自由模态分析和
3 数控转塔冲床瞬态响应分析
3.1瞬态响应分析基本理论
瞬态分析实际上只是在指定的时间点上通过求解下式来计算结构的响应。

(1)
式中:K为全局刚度矩阵;M为全局质量矩阵;B为阻尼单元确定的阻尼矩阵[4]。
(2)
本文通过阻尼表格TABDMP1列出了阻尼值相对于固有频率的值,将阻尼单独施加在了各个模态点上。式(2)解耦后为:
(3)
式中:ξi=bi/(2miωi)为模态阻尼系数,其中bi为模态阻尼比;mi为模态质量;ωi为模态特征值。
3.2冲裁力的计算
冲裁是通过一对模具——冲头和凹模,利用冲压设备加压于其间的胚料,使之在其有一定间隙的刃口处产生剪切等变形,进而分离破裂的冲压加工分离工序[5]。在冲裁加工中变形的区域非常小,变形力集中,变形过程涉及弹塑性变形和断裂问题,所以冲裁工艺的数值模拟是一个很复杂的问题。
本文利用DEFORM-2D软件进行冲裁工艺的数值模拟,胚料选择SUS304(304不锈钢),胚料厚度为4mm,凹模直径为φ41mm,冲头直径为φ40mm,双边冲裁间隙为1mm,冲孔频次为330次/min,冲程为6mm,冲头的平均速度为110mm/s,胚料为弹性材料,冲头和凹模为刚性材料,所以只需要对胚料划分网格,单元类型选择四节点单元,单元总数为3 955个。为了避免胚料断裂时胚料体积的大量流失以及主要变形区的精确模拟,在划分网格时对于主要变形区进行局部网格细划分,采用1∶0.4∶0.1∶0.05的网格划分比例。同时为了防止在剪切变形的过程中变形区网格的过度变形和网格的穿透,在分析过程中设置相互穿透网格最大尺寸为0.032 195mm,即相互穿透网格最大尺寸超过0.032 195mm时网格自动重划分。DEFORM-2D软件提供了10种断裂准则,本文所选用的断裂准则为Normalized C&L准则,C值取3.5[6]。冲裁工艺有限元模型如图3所示。

图3 冲裁数值模拟有限元模型
冲裁工艺数值模拟过程以及铅直方向冲裁力时间历程曲线分别如图4~图8所示,总共4个过程:第一阶段为冲击压缩阶段,材料相应处出现圆角,冲头和凹模的棱角处应力较大,冲裁力迅速增加;第二阶段为压入剪切阶段,应力集中面积迅速扩大,冲裁力在某一时刻增加到最大;第三阶段为裂纹生长阶段,胚料上被冲头棱角和凹模棱角压入的部位首先出现裂纹并同时向中间生长,产生断面毛刺,并且冲裁力不断减小;第四阶段为突然分离阶段,裂纹汇合,毛胚断裂,冲头突然卸载,冲裁力急剧减小[7]。

图4 冲击压缩阶段

图5 压入剪切阶段

图6 裂纹生长阶段

图7 突然分离阶段

图8 铅直方向冲裁力时间历程曲线
3.3冲床瞬态响应分析
本文的瞬态响应分析采用的是基于模态叠加法,除了需要进行模态分析还需要确定系统的阻尼值,这里采用系统的近似模态阻尼,由于数控转塔冲床的机身是焊接钢板结构,属于弱阻尼系统,近似取各阶振型的阻尼比ξ=0.01,β=2ξ/(2π×f),从模态分析可得主振型的频率f,从而计算出β阻尼为1.3e-4。
对于系统的冲击冲裁力,本文选择3个连续的冲压周期时间段,总时间为0.545 6s,分为100个时间步。数控转塔冲床上安装伺服液压缸和冲头的主板承受向上的周期性循环动态冲裁力作用,同时底部安装模具转盘的支撑板承受向下的周期性动态冲裁力作用,另外系统还承受向下的重力作用,这3个载荷是整个数控转塔冲床的外载激励源,通过Radioss BulkDate求解器的Tload载荷卡片建立动态载荷,同时将2个动态载荷以及1个重力载荷集成在1个载荷步里面。
由瞬态分析的结果可得最大位移时间历程曲线如图9所示。
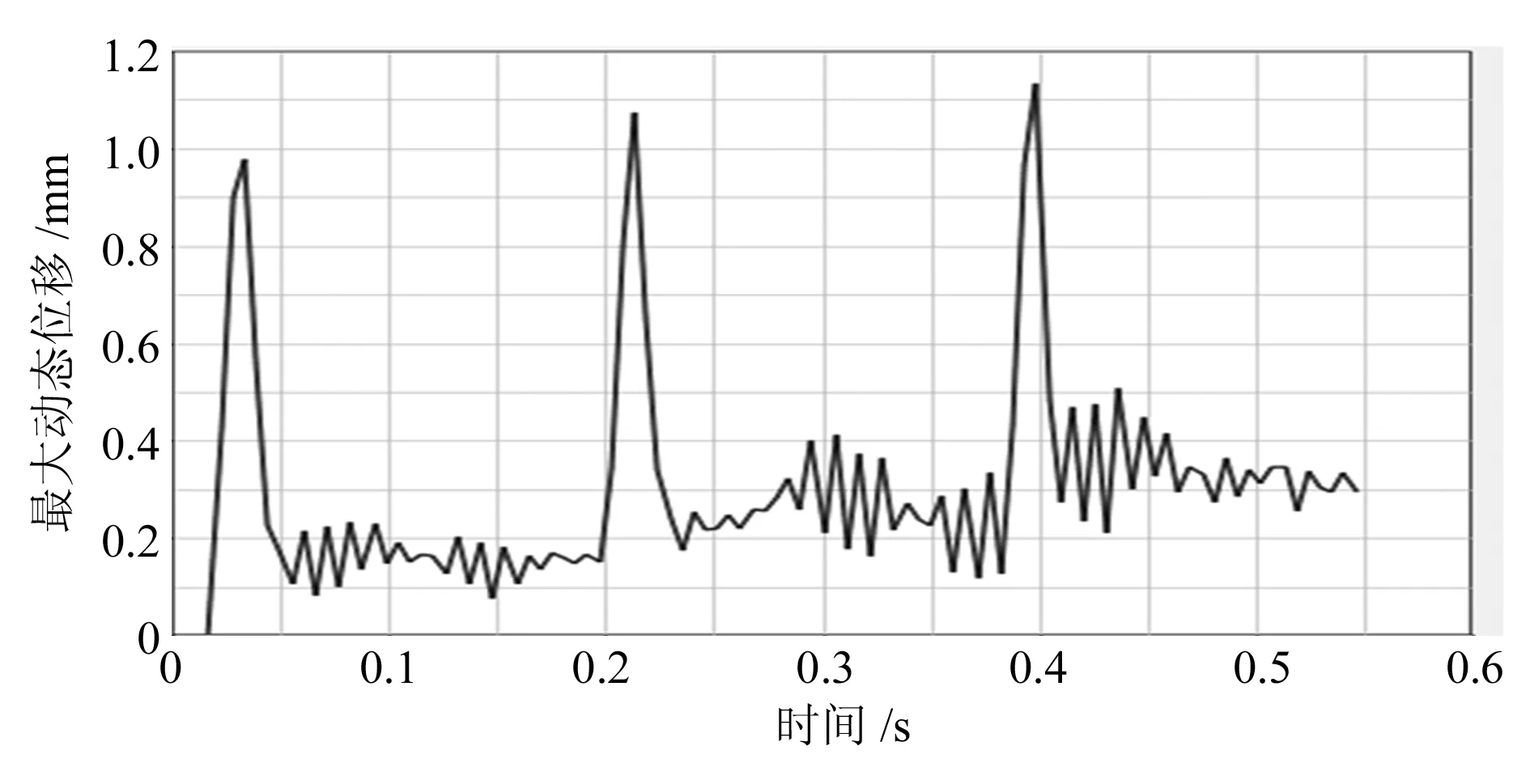
图9 最大位移时间历程曲线
最大应力时间历程曲线如图10所示。

图10 最大应力时间历程曲线
由图9可知,冲床机身最大动位移约为1.15mm,第一个周期振动最为剧烈的时刻最大位移约为0.99mm,第二个周期振动最为剧烈的时刻最大位移约为1.09mm,而第三个周期振动最为剧烈的时刻最大位移增加到1.15mm,由此可知机床振动越来越剧烈,同时由图9可知,第一个周期的振动相对于第二个、第三个周期衰减较快,第二个周期衰减最慢。由图10可知,机床机身的最大动应力约为74.8MPa,也是第三个周期的时候最大动应力最大,动应力衰减也是第二个周期相对较慢。
在图1中标注的6个节点的位移时间历程曲线如图11~图16所示。

图11 Node1 3个方向的位移时间历程曲线

图12 Node2 3个方向的位移时间历程曲线

图13 Node3 3个方向的位移时间历程曲线

图14 Node4 3个方向的位移时间历程曲线

图15 Node5 3个方向的位移时间历程曲线
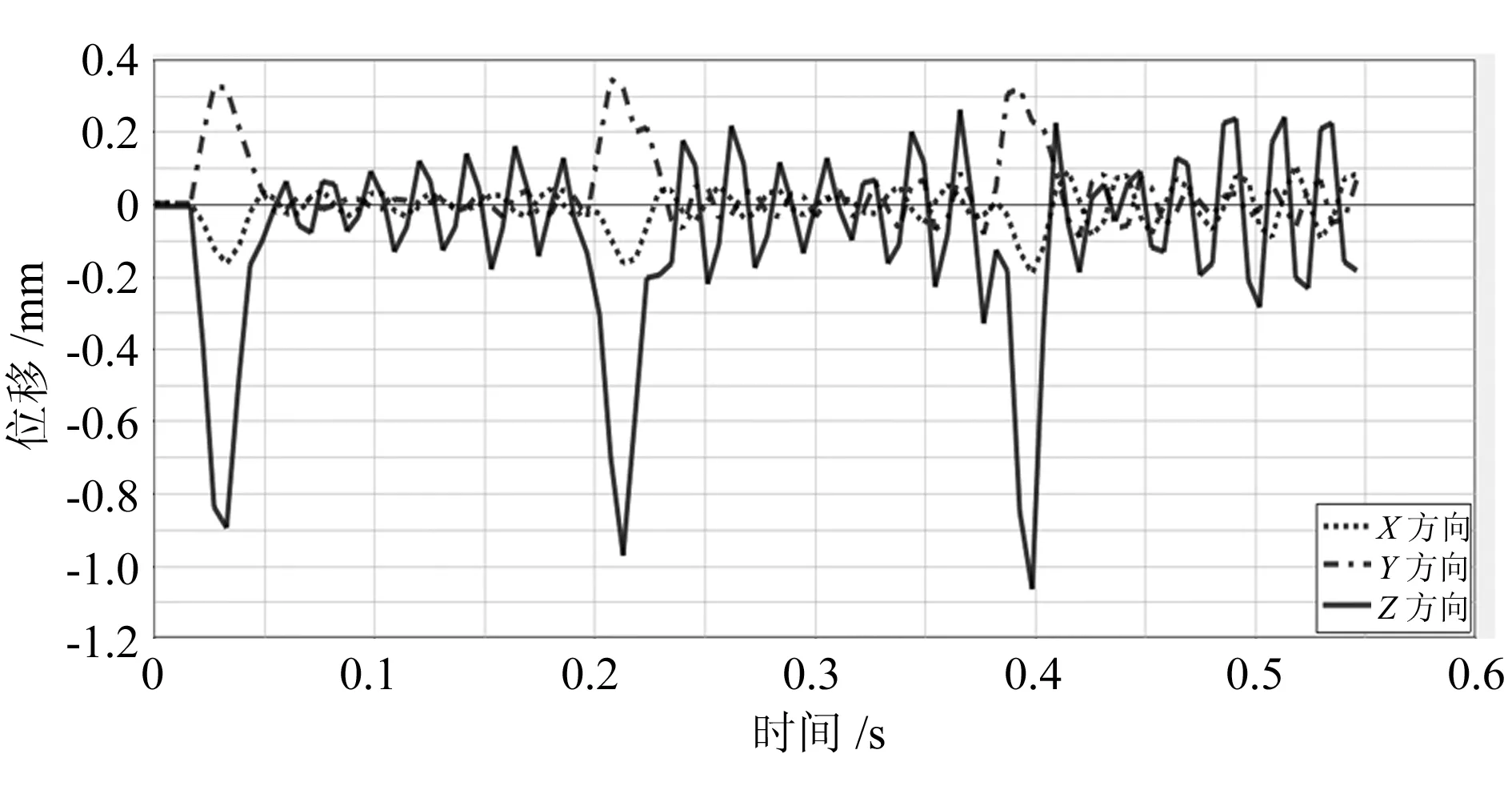
图16 Node6 3个方向的位移时间历程曲线
Node1和Node2分别为冲头的中心节点和下模的中心节点,由图11和图12可知,Node1的最大变形为0.46mm,Node2的最大变形为0.16mm,Node1的位移分别在0.027 28s、0.2127 8s、0.451 47s 3个时间点出现峰值,Node2的位移分别在0.027 28s、0.218 24s、0.398 29s3个时间点出现峰值,其他时刻的变形大多在0.06mm左右,相对较小,另外这2个节点的动态变形主要在Y方向,在Z方向和X方向的变形都相对较小;Node3和Node4这2个节点位于横梁支撑平台的导轨边沿,它们的振动对于横梁的振动影响比较大,由图13和图14可知,Node3的最大变形为0.28mm,Node4的最大变形为0.22mm,这2个节点的振动衰减都较慢,而且主要变形在Y方向,至于其他2个方向的变形则更小,同时这2个节点的振动基本同向;Node5和Node6为主墙板上加强筋上方的2个节点,这2个节点的主要变形集中在Z方向,最大位移都在1.09mm左右,振动较为剧烈,而且基本都在0.003 27s、0.212 80s、0.398 30s这3个时间点出现最大值,同时在Y方向的最大位移在0.34mm左右,3个位移峰值基本相等,至于X方向变形相对比较小。
综上可知,在动态载荷的作用下,数控转塔冲床的动态位移和动态应力都相对较大,而且在机床安装冲头一侧的上半部分的Z方向和Y方向振动最为激烈,特别是Z方向最大位移达到了1.09mm,这对于冲头的在Z方向的定位精度影响较大,可见这一部分的动刚度相对较低,需要做一定程度的结构改进。
图17为前二十阶模态的模态参与因子随时间变化的三维曲面图,由图可知在3个振动最为激烈的时间点,主要是二阶、三阶、四阶、六阶、八阶、十阶、十三、十九阶模态的模态参与因子的绝对值相对较大,而这8个模态的振型主要是安装模具一侧的主墙板在Z方向的弯曲振动以及横梁支撑平台在Y方向的振动。所有模态参与因子组成的向量与各阶模态振型向量的矢量积即为当前时刻的振动,所以模态参与因子可以理解为对应模态对当前时刻振动的贡献量[8],这样就可以有针对性地对这8个模态进行控制,改变这几阶模态的频率,避开外界激励频率,降低它们的贡献量,或者减小它们的相对振动,以减小系统总体的振动[9]。
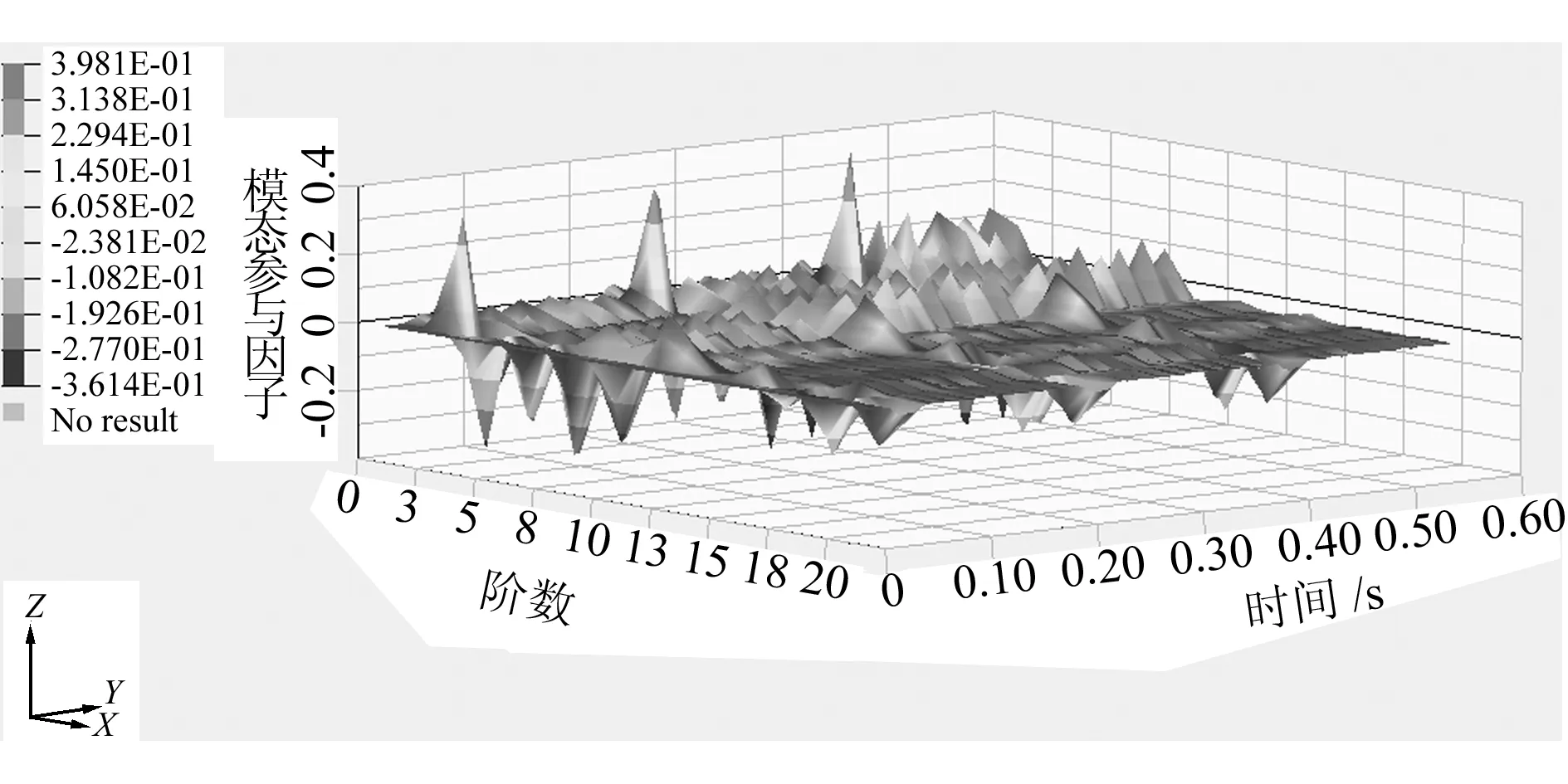
图17 前二十阶模态的模态参与因子
4 结束语
本文将实验与有限元仿真相结合,建立了准确的有限元模型,创造性地利用冲裁工艺数值模拟计算冲裁力,并将其应用于冲床的瞬态响应分析。根据模态分析和瞬态分析的结果,找到了系统的薄弱环节,为进一步的振动研究和优化奠定了基础,同时也为冲床的设计提供了依据。
[1] 季忠,高训涛,孙胜,等.闭式数控压力机机身动态响应分析[J].锻压机械,2001(1):38-40.
[2] 谢君翌.数控转塔冲床机身的有限元分析与优化设计[D].南京:东南大学,2005.
[3] 龚立新,胡金龙,吴长明,等.数控转塔冲床动态特性研究[J].锻压装备与制造技术,2014(1):20-22.
[4] 欧贺国,方献军,洪清泉,等.RADIOSS理论基础与工程应用[M].北京:机械工业出版社,2012.
[5] 戴源德.冲裁工艺噪声发射及其控制的理论与实验研究[D].南昌:南昌大学,2007.
[6] 陈辉.基于伺服压力机的厚板变速冲裁工艺研究[D].广州:广东工业大学,2013.
[7] Ghiotti A,Regazzo P.Reduction of vibrations in blanking by MR dampers [J].CIRP Annals - Manufacturing Technology,2010, 59(1):275-278.
[8] 张开银,陈建辉,刘军辉.基于模态分析技术的结构动应力研究[J].武汉理工大学学报,2007,31(6):991-992.
[9] Gih Keong Lau,Du Hejun.Topology optimization of head suspension assemblies using modal participation factor for mode tracking[J]. Microsyst Technol,2005,11 (12): 1243-1251.
TheDynamicCharacteristicAnalysisontheFrameofCNCTurretPunchPress
ZOU Yao, TANG Wencheng
(Southeast University, Jiangsu Nanjing, 211189, China)
In order to study the frame' vibration of CNC turret punch press, it takes the HPR - 3048 CNC turret punch press as an example, discusses the finite element modal analysis and experiment modal analysis of the frame, establishes an accurate finite element model. Meanwhile through the plastic forming software DEFORM, it obtains the time history curve of the die' cutting force when the punch is punching. Then taking this curve as the dynamic load and computing the dynamic response of the punch through the modal superposition method, it shows the time history curves of the maximum dynamic stress, the maximum dynamic displacement and several key nodes, and provides the 3D surface of modal participation factor' time history, gives the practical guidance for reducing the vibration of the punch.
CNC Turret Punch Press; Finite Element Modal Analysis; Experiment Modal Analysis; Punching Processes; Transient Analysis
10.3969/j.issn.2095-509X.2014.07.007
2014-07-07
邹瑶(1988—),男,湖北麻城人,东南大学硕士研究生,主要研究方向为结构分析与优化。
TH113.1
A
2095-509X(2014)07-0029-06

