间隙对两轴液压振动试验系统动力学影响的研究

文 祥, 陈章位, 贺惠农

(1. 上海卫星装备研究所，上海 200240；2.浙江大学 流体动力与机电系统国家重点实验室，杭州 310027；3.浙江大学 生物医学工程与仪器科学学院，杭州 310027)

在动力学系统中很多运行因素会导致间隙, 间隙的存在会使系统在工作时机构间产生碰撞。含间隙的碰撞振动系统一般为多参数高维的, 且具有强的非线性和不连续性, 使系统的动态行为变得十分复杂, 致使许多工程结构失效, 也给传统结构振动分析及其分析结论的实际运用都造成很大困难[1]。国内外学者在间隙内碰撞非线性模型以及一些典型含间隙机构动力学建模方面做了大量的研究工作，阎绍泽等[2]对含间隙铰的机械多体系统动力学模型展开了研究，对四类间隙铰模型(连续接触模型、有限元模型、经典碰撞模型和接触变形模型)进行了分析比较, 给出了经典碰撞和接触变形模式的含间隙多体系统动力学模型。李哲[3]对含间隙机构混沌响应进行了实验研究，分析了动态响应受运动副间隙尺寸大小和输入速度大小的影响。张跃明等[4]对空间机构间隙转动副进行了建模，分析了间隙转动副所有可能存在的模式, 并运用力学分析的方法得出了模型每种模式的存在条件。郝雪清等[5]研究了不同运动副材料对间隙机构动力学特性的影响，利用非线性等效弹簧阻尼的概念建立了含间隙运动副的接触动力学模型并进行了仿真研究。Flores等[6]对含间隙运动副的多体系统动力学特性进行了数值仿真和实验研究，并将数值仿真结果与实验结果进行了对比分析。Tasora等[7]研究了不同间隙尺寸下曲柄滑块机构的动力学响应，并通过实验进行了验证。Turcic等[8]对弹性四杆机构展开了实验研究，分析了曲柄不同转速和频率下系统应变的响应。近年来，国内外的学者对含间隙运动副的机构动力学展开了深入的理论研究，但实际机构的运动副中的间隙通常很小,运动副间隙所引起的系统运动非常复杂, 不同系统运动副中的各种物理参数也很难准确给定，这些因素都给解析分析带来一定的困难, 因而对含间隙机构进行实验研究显得特别重要,也就是说， 关于含间隙机构的理论研究成果, 只有得到实验的支持才变得更为可靠，但目前对含间隙副的振动试验系统的非线性动力学行为的实验研究还不够深入。

液压振动试验系统本身具有很强的非线性， 在简谐激励下响应状态复杂, 实际振动试验中，由于信号误差、振动台制造误差，两液压振动台之间总是存在异步误差，尤其在中、高频率振动环境工作时，异步误差表现尤为突出，为了能够有效保证振动台和试件的安全，夹具的一侧设计了一个可以自由转动的支耳，如图1所示。由于支耳作为夹具中的一部分，在设计的时候，支耳和测试杆之间有相对转动，运动副之间为动配合，这就存在一定的运动副间隙，运动副间隙导致运动副元素之间发生猛烈冲击和碰撞, 增加构件的动应力,系统响应既有各种不同的周期状态,还存在各种复杂的响应突变。

本文的研究对象是两个液压振动台对细长杆试件进行多点激励振动试验的系统，建立了含间隙副的两轴液压振动试验系统碰撞副力学模型，采用ADAMS进行动力学仿真，并通过实验进行了验证，分析了测试杆在异步简谐激励下，测试杆的动力学响应随激振频率、激振幅值的演变规律，为理论研究和多轴振动试验提供了依据。

图1 两轴液压振动试验系统

1 间隙副力学模型

对于一些在实际工作或运输环境下，受到的激励点不止一个的产品或设备，如导弹、火箭和鱼雷等产品常需要多点激励振动试验。单点激励无法全面模拟其振动情况，多点激励振动试验将成为一种不可替代的试验手段。本实验中，两轴液压振动试验系统对测试杆进行两轴激励试验，测试杆通过转动副连接在支耳和底座上。两轴激励振动试验使试件的振动载荷分布更加均匀、合理、真实，减少单点激励带来的应力集中，减少局部欠试验和过试验程度，同时使夹具设计更加灵活方便。

1.1 间隙转动副定义

理想情况下, 转动副是理想副，轴和轴承同心且没有间隙。但在实际情况下，为了允许轴和轴承的相对转动，一定量的间隙总是存在。图2描述了轴和轴承间隙副，RB表示轴承的半径,RJ表示轴的半径，为了更加清楚地表达间隙的存在，图中的间隙放大画出，间隙的定义为:

c=RB-RJ

(1)

图2 含间隙转动副(间隙夸大)

1.2 连续碰撞力模型

在间隙运动副的轴和轴承中, 通常包括以下三种运动状态:① 自由运动,轴在轴承里自由运动而不发生接触;② 碰撞, 轴和轴承发生接触时产生碰撞力, 非接触时没有碰撞力;③ 连续接触, 轴和轴承始终接触,如图3所示。

图3 轴在轴承内部的运动类型

具体来讲，在连续接触阶段，轴和轴承的表面始终处于接触状态或相对滑动状态，并沿着轴承内表面沿圆周方向有相对穿透深度。当这种运动状态结束后，轴和轴承开始分离，轴开始进入自由运动阶段，也就是说，轴和轴承之间不再相互接触，运动副之间不会有相互作用力，轴可以在轴承内部自由运动。自由运动结束后，轴和轴承开始进入碰撞阶段，碰撞力作用在系统上，轴和轴承之间的动量发生很大的变化，系统的运动和动力学特性呈现不连续性。当碰撞结束后，轴要么进入自由运动状态要么进入连续接触状态[9-12]。图3表达了运动的各种状态。

当轴和轴承发生碰撞后，轴和轴承之间会产生法向力FN和切向力FT,且这些力通过机械系统传递。图4显示了轴和轴承碰撞引起的切向力和法向力。碰撞引起的穿透深度可以定义为：

δ=eBJ-C

(2)

式中：eBJ为轴和轴承中心的偏心矢量的大小，C为间隙尺寸。

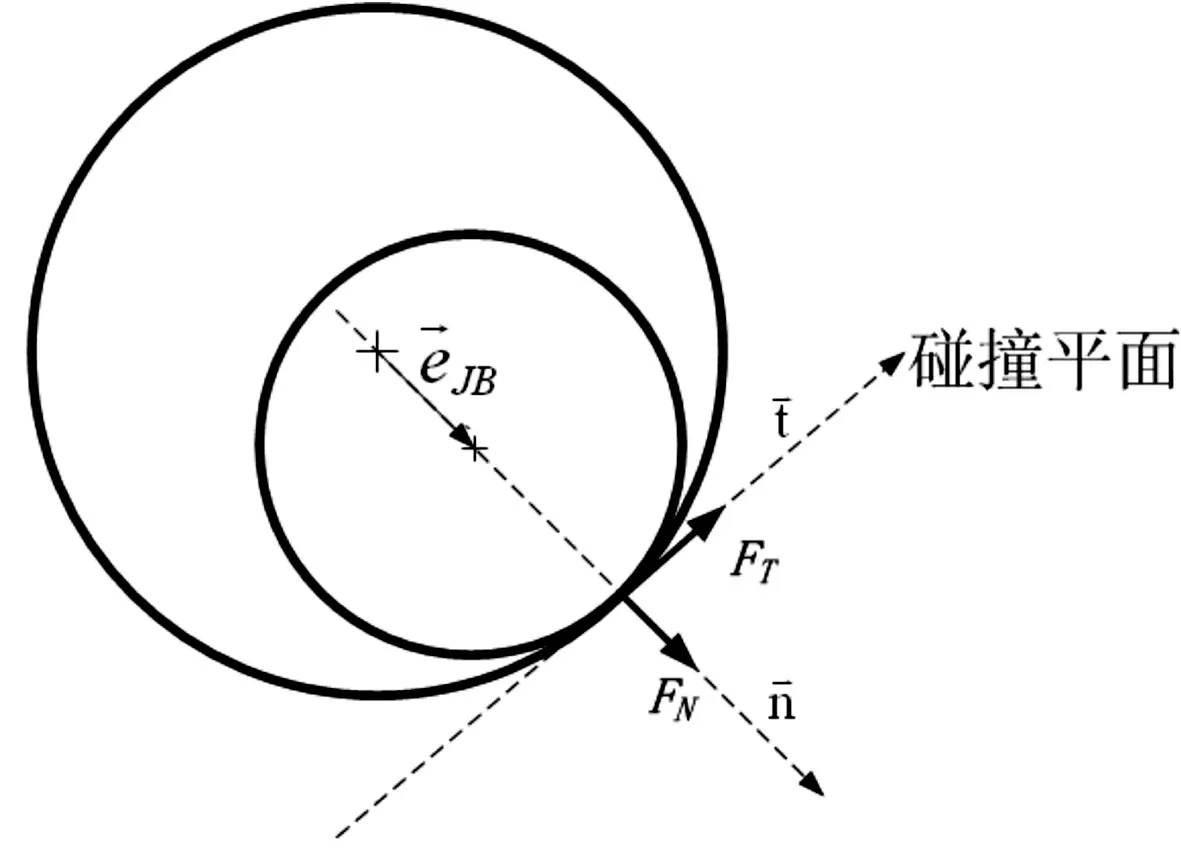
图4 法向和切向碰撞力

连续碰撞力模型考虑了轴和轴承碰撞过程中的动态变化[13]。在这个模型中，积分时间步长应该比碰撞时间要短，当轴和轴承发生碰撞时，轴相对于轴承有一个穿透深度，碰撞力取决于瞬间的穿透深度和穿透速度。连续碰撞力模型主要用于模拟碰撞时间很短的物理过程，目前为止，很多文献提供了多种基于连续碰撞力模型的法向力的计算方法，其中，Hertz模型普遍被采用，但它只考虑了碰撞刚体件的弹性本质，没有考虑碰撞过程中的能量耗散。Lankarani 和Nikravesh 在计算过程中考虑了结构阻尼，因此可以获得包含能量耗散项的法向力计算关系式：

(3)

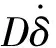
(4)

其中材料参数σB，σJ为：

(5)

式中：νz为泊松比，Ez为碰撞体材料的杨氏弹性模量，Hunt和Crossley将滞环阻尼系数表示为：

D=Hδn

(6)

式中：H为滞环阻尼因子，对于两个圆柱形的碰撞体，H可以表示为：

(7)

2 数值仿真和实验分析

为了分析间隙对两轴液压振动试验系统动力学响应的影响，将系统模型嵌入到ADAMS动力学软件中进行仿真研究，如图4所示，两激振器处于异步状态。图5清楚地表达了系统中试验对象和激振器系统以及夹具之间的连接关系。底座1通过螺栓固定在激振器台面1上，底座2通过螺栓固定连接在台面2上，测试杆左端和底座1通过转动副连接，测试杆右端和支耳通过转动副连接，且测试杆右端和支耳相连接的转动副存在间隙(通过更换轴可以改变间隙的大小，为了获得参考数据，特别加工了一个轴，使得轴与轴承之间的间隙为0)，间隙尺寸C=0.8 mm，其余运动副为理想副。

图4 双轴液压振动试验系统在ADAMS中的模型(异步状态)

图5 双轴液压振动试验系统结构简图(异步状态)

为了验证仿真的有效性，搭建了一套双轴液压振动试验系统，现场如图6(a)所示，整个系统由MIMO振动控制器(杭州亿恒科技有限公司生产的PREMAX,同时具备数据采集功能)、ICP传感器2个、双轴液压振动台、底座1、底座2、测试杆。如图6(b)所示ICP传感器1(CA-YD-186)垂直安装在支座1上， ICP传感器2(PCB SN55125)垂直安装在支耳上。支耳和底座2通过转动副连接，激振器1和激振器2分别做简谐运动。

图6 (a)实验现场

图6 (b)加速度数据采集系统

仿真和实验过程中，激振器1和激振器2的输入均为简谐激励，两个激振器处于异步状态，激振器1的输入为y=Asin(2*pi*ω*t)，激振器2的输入为y=Asin(2*pi*ω*t+φ)，实验主要针对相位差大小φ为45°的异步激振下，不同激振频率ω、不同激振幅值A对系统动力学响应的影响，本实验关注垂直方向的加速度响应，其它方向不予考虑。

系统中各部件的几何参数和惯性特性如表 1所示，系统动力学实验参数见表2：

表1 双轴液压振动试验系统主要特性

表2 双轴液压振动试验系统仿真参数

3 结果和分析

3.1 不同激振频率下的加速度响应

当间隙尺寸C=0.8 mm时，激振器1的输入为y=5sin(2*pi*ω*t)，激振器2的输入为y=5sin(2*pi*ω*t+45°)，通过改变激振器输入激振频率的大小ω,综合分析系统的加速度输出响应，仿真和实验结果如图7所示。

图7 激振频率分别为ω=5 Hz，ω=10 Hz，ω=20 Hz时，加速度响应

图7给出了系统加速度的响应，蓝色虚线和黑色虚线分别为ADAMS中底座1和支耳的仿真输出加速度，红色实线和绿色实线分别表示间隙尺寸c=0.8 mm时，底座1和支耳的输出加速度，仿真和实验结果表明，在间隙尺寸一定的情况下，两个激振器相位差为45°时，随着简谐输入激振频率的增加，每半个周期，也就是激振器换向的时候，间隙处都发生剧烈碰撞，可以看出峰值加速度急剧增加，由于激振器的异步，产生了耦合振动效应，且随着频率的增加，底座1的加速度峰值和支耳上的加速度峰值都在增加，但底座1的加速度峰值要大于支耳上的加速度峰值，底座1上的峰值加速度甚至可以达到3倍以上，同时还可以看出，随着激振频率的增加，间隙副处的碰撞次数增加，加速度响应曲线的“毛刺”越来越多。

3.2 不同激振幅值下的加速度响应

当间隙尺寸C=0.8mm时，激振频率为10Hz时，激振器1的输入为y=Asin(2*pi*10*t)，激振器2的输入为y=Asin(2*pi*10*t+45°)，通过改变激振器输入幅值的大小A,综合分析系统的加速度输出加速度响应，仿真和实验结果如图8所示。

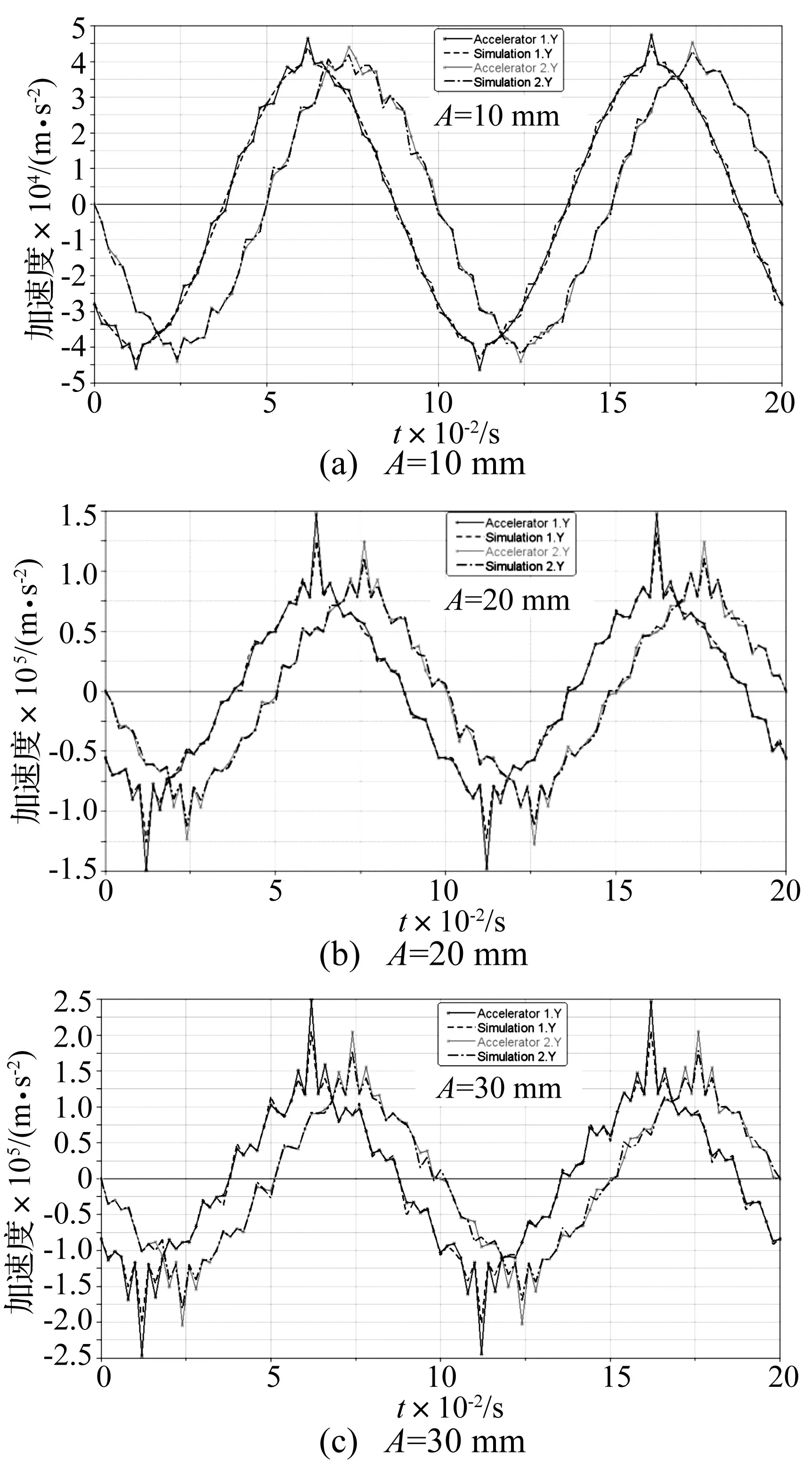
图8 激振幅值分别为A=10 mm， A=20 mm， A=30 mm时，加速度响应

图8给出了系统加速度的响应，蓝色虚线和黑色虚线分别为ADAMS中底座1和支耳的仿真输出加速度，红色实线和绿色实线分别表示间隙尺寸C=0.8 mm时，底座1和支耳的输出加速度。仿真和实验结果表明，在间隙尺寸一定的情况下，两个激振器相位差为45°时，随着简谐输入激振幅值的增加，每半个周期，也就是激振器换向的时候，间隙处都发生剧烈碰撞，可以看出峰值加速度显著增加，由于激振器的异步，产生了耦合振动效应，随着激振幅值的增加，底座1的加速度峰值和支耳上的加速度峰值都在增加，但底座1的加速度峰值要大于支耳上的加速度峰值，底座1上的峰值加速度可达到2倍以上，同时还可以看出，与激振频率影响系统响应不同的地方是，随着激振幅值的增加，加速度响应曲线的“毛刺”相对较少，说明在一定的时间范围内，间隙处的碰撞次数相对较少。

4 结 论

本文建立了基于Lankarani 和Nikraves的连续碰撞力学模型，采用ADAMS动力仿真软件对两轴液压振动试验系统的动力学特性进行了数值仿真分析，并通过实验进行了验证，仿真和实验结果表明：

(1)两轴液压振动试验系统的动力学响应受间隙尺寸的影响，在激振器异步且间隙尺寸一定的情况下，由于激振器的异步，产生了耦合振动效应，系统的稳态加速度响应有明显的变化，加速度输出会出现抖动的“毛刺”，这是间隙引起的转动副间碰撞的结果。

(2)激振器输入激振频率对系统的动力学响应影响很大。随着激振频率频率的增加，底座1的加速度峰值和支耳上的加速度峰值都在增加，但底座1的加速度峰值要大于支耳上的加速度峰值，底座1上的峰值加速度甚至可以达到3倍以上。因此，对多轴激振实验而言，合理设计转动副间隙从而消除由于间隙副的非线性因素的影响非常重要。

(3)在间隙尺寸一定的情况下，随着激振幅值的增加，底座1的加速度峰值和支耳上的加速度峰值都在增加，但底座1的加速度峰值要大于支耳上的加速度峰值，底座1上的峰值加速度可达到2倍以上，与激振频率影响系统响应不同的地方是，随着激振幅值的增加，加速度响应曲线的“毛刺”相对较少，说明在一个在周期内，间隙处的碰撞次数相对较少。

参 考 文 献

[1]曹妍妍, 赵登峰.间隙约束悬臂梁系统的动力学行为实验研究[J]振动与冲击，2007,26(4):154-157.

CAO Yan-yan, ZHAO Deng-feng. Experimental study on dynamic characteristic of a cantilever beam system with clearance restriction[J]. Journal of Vibration and Shock, 2007,26(4):154-157.

[2]阎绍泽，陈鹿民,季林红,等。含间隙铰的机械多体系统动力学模型[J].振动工程学报，2003,16(3):290-294.

YAN Sao-ze, CHEN Lu-min, JI Lin-hong, et al. Dynamic modeling of multibody system with clearance joints[J]. Journal of Vibration Engineering, 2003,16(3):290-294.

[3]李 哲，张 渊.含间隙机构混沌响应的实验研究[J].北京工业大学学报, 1994,20(4):33-38.

LI Zhe, ZHANG Yuan . Experimental research of on the chaotic responses of mechanisms with clearances[J]. Journal of Beijing Polytechnic University, 1994,20(4):33-38.

[4]张跃明，唐锡宽,张兆东，等.空间机构间隙转动副模型的建立[J].清华大学学报,1996;36(8):105-109.

ZHANG Yue-ming, TANG Xi-kuan, ZHANG Zhao-dong, et al. Modeling of revolute joint with clearances in spatial mechanism[J]. Journal of Tsinghua University(Sci&Tech)1996;36(8):105-109.

[5]郝雪清，陈江义.不同运动副材料对间隙机构动力学特性的影响[J].振动与冲击，2012,31(12):19-21.

HAO Xue-qing，CHEN Jiang-yi. Effects of different materials in joints on dynamic characteristics of a mechanism with clearance[J]. Journal of Vibration and Shock,2012,31(12):19-21.

[6]Flores P, Koshy C S, Lankarani H M, et al. Numerical and experimental investigation on multibody systems with revolute clearance joints[J]. Nonlinear Dynamics, 2011,65(4):383-398.

[7]Tasora A, Prati E, Silvestri M. Experimental investigation of clearance effects in a revolute joint：Proceedings of 2004 AIMETA International Tribology Conference, ed. Aracne, ISBN, 2004[C]. Citeseer.

[8]Turcic D A, Midha A, Bosnik J R. Dynamic analysis of elastic mechanism systems. II：Experimental results[J]. Journal of Dynamic Systems Measurement and Control, 1984,106(4):255-260.

[9]Flores P. Modeling and simulation of wear in revolute clearance joints in multibody systems[J]. Mechanism and Machine Theory, 2009,44(6):1211-1222.

[10]Flores P, Leine R, Glocker C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach[J]. Multibody System Dynamics, 2010,23(2):165-190.

[11]Khemili I, Romdhane L. Dynamic analysis of a flexible slider-crank mechanism with clearance[J]. European Journal of Mechanics-A/Solids, 2008,27(5):882-898.

[12]Tasora A, Prati E, Silvestri M. A Compliant Measuring System for Revolute Joints with Clearance：Ait-aitc 2006, 2006[C]. Citeseer.

[13]Megahed S M, Haroun A F. Analysis of the dynamic behavioral performance of mechanical systems with multi-clearance joints[J]. Journal of Computational and Nonlinear Dynamics, 2011,7(1):011002.