汽车撞击桥墩瞬态撞击力的等效静力计算

崔堃鹏， 夏 禾， 夏超逸， 吴 萱

(北京交通大学 土木建筑工程学院，北京 100044)

随着公路、铁路、城市立交桥的大量建设，跨线桥数量剧增，桥墩被汽车撞击的可能性大大增加。桥梁受到汽车等撞击时，可能会引起支座与主梁的错位，使伸缩缝变形不协调，伸缩缝断裂，给桥梁结构埋下安全隐患，严重时会直接导致桥梁的塌落，后果极其严重。譬如，对于高速铁路桥梁，桥墩受到撞击时，桥梁结构即使不发生塌落，也将发生一定的振动和位移，从而影响桥上线路的平顺性和稳定性，造成桥上行车安全问题。

撞击过程是一个瞬态动力作用，工程往往将动力作用转化为一个静力荷载进行设计。中国《高速铁路设计规范(试行)》(TB10621-2009)和《公路桥涵设计通用规范》(JTG D60—2004)中规定：对遭受汽车撞击而无防撞措施的桥梁墩台，应检算汽车撞击状态，顺汽车行驶方向的撞击力应采用1 000 kN，垂直于汽车行驶方向的撞击力应采用500 kN，两个等效力不同时考虑，作用在路面以上1.2 m高度[1-2]。美国AASHTO 2007年颁布的《LRFD bridge design specifications,4th edition》中规定：位于距道路边缘9 m以内或距铁路轨道中心线15 m的桥梁墩台，未安装防护装置时，设计时应考虑1 800 kN的车辆撞击力，该力在地面以上1.2 m位置从任意方向水平作用于结构[3]。这些规范并未给出这些等效静力的来源及合理性，美国规范只是阐明规定源自于早期的足尺测试实验，也未考虑提及汽车桥墩撞击动力相互作用。

国内外关于船舶撞击桥墩撞击力时程等特性已有相关研究[4-5]，并且规范给出计算方法，很多学者也发表相关经验公式，但是关于汽车撞击桥梁的研究很少，公路、铁路规范也没有给出动态撞击力计算方法。

车辆与桥梁结构碰撞的作用机理复杂，涉及几何非线性、材料非线性、接触非线性以及动力效应问题，理论研究的难度非常大，实验研究破坏性大、费用昂贵，英国Arup公司的车辆撞击桥梁桥墩和上部结构的足尺试验数据只是作为企业内部的研究报告，尚未公开[6]。澳大利亚昆士兰大学Thilakarathna等[7]采用非线性数值分析模型，研究了车辆对墩柱的撞击作用，获得了撞击力时程曲线、结构位移和支座反力等分析结果。Buth[8]等统计了美国重型汽车撞击桥梁事故，通过数值模拟研究分析了美国规范对应限值存在的风险性和准确性。清华大学陆新征等[9-10]基于精细化非线性有限元分析，研究了超高车辆撞击桥梁上部结构的损坏机理，给出了撞击力时程。目前多数研究还是采用有限元模拟手段，没有考虑动力与静力相互转化作用，并且在动力研究中没有明确给出激励荷载。

汽车撞击是一个瞬态过程，撞击过程一般不超过0.2 s，撞击力的峰值出现在碰撞过程中的某一个时刻。在实际工程设计中，需要把这样一个瞬态撞击过程力等效成一个静力荷载。本文拟通过研究比较几种将动态力转换成等效静力的方法，与规范限值进行比较，探讨其中可能存在的问题。研究中采用ANSYS LS_DYNA建立了互通立交桥墩模型和Ford卡车模型，模拟车辆以60km/h、80km/h、100km/h、120km/h四种不同撞击速度正向撞击桥墩侧面的过程，从中提取汽车撞击桥墩的碰撞过程撞击力结果，采用全局平均法、局部平均法、等效位移法、简化脉冲荷载法等四种汽车撞击力等效静力计算方法，计算了模拟撞击过程的等效静力值，并与既有工作和几种规范限值进行了比较，并在此基础上讨论了动力研究过程中输入激励问题。

1 有限元模型获取撞击力时程

ANSYS LS_DYNA运用显式算法能高效求解瞬时大变形动力学、大变形和多重非线性准静态问题及复杂的接触碰撞问题。LS_PrePost是与LS_DYNA配套的高级前处理程序和后处理程序，功能强大。

1.1 车辆模型

为更真实地模拟汽车撞击,采用美国国家碰撞中心NCAC(National Crash Analysis Center)发布的汽车有限元模型。汽车模型选取了一个约8 t重的Ford卡车，代表中型卡车，见图1。

汽车模型中，发动机、传动装置、散热器采用SOLID164实体单元，采用各向同性弹性材料模型*MAT_ELASTIC；车身和底盘等金属部件则采用SHELL163壳单元模拟，采用分段线性塑性模型*MAT_PIECEWISE_LINEAR_ PLASTIC。共有21400个单元、38949个节点。

图1 Ford卡车模型

1.2 桥墩模型

国道312线与苏州市某主干路交叉处设置一互通式立交，该互通上跨312国道主线桥第23号桥墩位于绿化带上，被下穿车辆撞击桥墩的可能性很大，选取此实际桥墩作为撞击研究对象。桥墩截面尺寸为180 cm×300 cm，高度为2 134 cm，C40钢筋混凝土，纵筋采用直径28 mm的HRB335钢筋，箍筋采用直径16 mm的HRB335钢筋，几何尺寸见图2。

图2 互通立交桥墩尺寸(cm)

桥墩有限元模型细部尺寸作简化处理，忽略顶部线性变化，采用整体式模型，solid164实体单元，混凝土材料本构模型采用Brittle_damage本构，其基于损伤力学理论，能够模拟混凝土拉伸断裂行为。

墩顶自由，仿真过程中暂时不考虑梁对桥墩约束和重力作用，实际桥墩被撞击过程中动力特性与上部结构的约束条件和质量关系很大，具体量化关系目前尚不明确，为研究方便，本文采取单墩模型。墩底与路面固结，采用映射网格划分，共288个单元。

1.3 碰撞实现过程

本文仅研究卡车正向直接撞击桥墩的情况，不考虑侧向及其它角度的撞击。鉴于中国国道限速60 km/h，高速公路限速为90～120 km/h，按车辆初速度60 km/h、80 km/h、100 km/h、120 km/h计算。

命令流保存成k文件(文件后缀名为k)，用LS_DYNA 971求解器加载求解，观察整个撞击过程，提取碰撞接触面的撞击力时程及峰值，分析计算结果，在Ls_PrePost后处理中，可以方便地看到模拟的撞击全部过程。图3为Ford卡车在速度120 km/h时，撞击力峰值对应的汽车撞击桥墩视频截图，车头变形过程清晰可见。

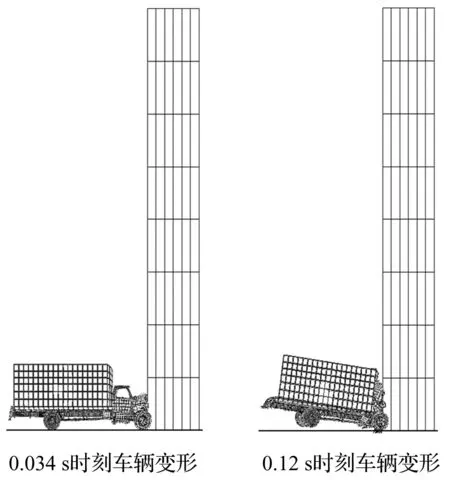
图3 峰值时刻Ford卡车撞击桥墩截图(120 km/h)

1.4 撞击力时程曲线和峰值

1.60km/h，峰值2.85MN；2.80km/h，峰值3.99MN；3.100km/h，峰值7.34MN；4.120 km/h，峰值13.80MN

图4是 Ford卡车撞击力随不同车速的分布，可以看出，撞击力总的持续时间约为0.20 s，但峰值表现为窄脉冲荷载的形式，宽度只有0.01～0.02 s左右。撞击力时程增长与速度近似线性关系，Ford卡车出现3个峰值，是因为Ford卡车在与桥墩发生撞击时，车头前部先变形，然后后面车体对桥墩进行二次撞击的原因,并且速度越高，车厢二次撞击尾部峰值越高。车辆每个部分在参与碰撞过程中是否发挥作用和先后失效决定了撞击力时程峰值的出现。

车速越高，峰值出现得越早，脉冲宽度越窄；峰值撞击力随车速的提高而迅速增大，速度120 km/h时最大峰值为13.80 MN。

2 等效静力计算方法

车辆撞击是一个动态过程，撞击力最大值或者峰值出现在碰撞过程中的某一特定时刻，在工程设计中，往往需选择适当的方法将这样一个动态撞击过程等效成一个静力荷载作用，本文经过研究，提出以下几种等效静力方法，并通过实际计算对比来研究各种方法的可行性。

2.1 全局平均法计算等效静力

全局平均法是指在整个时域内总体平均值，对撞击力时程p(t)在时域内积分，然后与撞击持续时间tt的比值作为等效静力Pt，即:

(1)

采用这种计算方法，对应Ford卡车四种不同速度的等效静力为：Pt60=0.03 MN，Pt80= 0.04 MN，Pt100=0.05 MN，Pt120=0.07 MN。

2.2 局部平均法计算等效静力

局部平均法是指在两个峰值或者波谷撞击力p(t)在时刻(t1～t2)之间时域内的平均值，对该时间段撞击力时程在时域内积分，然后与撞击时间(t2-t1)的比值作为等效静力Pp，即:

(2)

对应Ford卡车四种不同速度的等效静力为：Pp60=0.13 MN，Pp80=0.15 MN，Pp100=0.31 MN，Pp120= 0.42 MN。

2.3 位移法计算等效静力

等效位移法求等效静力是指在力作用点，和对应动力荷载产生相同位移时所需静力的大小Pd，这取决于系统的刚度和动力特性。近似地，取卡车重心高度作为撞击点位置，也就是撞击面作用力的合力点，本例中取重心位置在路面以上1.4 m处(模型车辆重心约在1.4 m处)，在Ls_PrePost提取撞击面撞击力合力时程曲线p(t)和弯矩时程曲线M(t)，在ansys中建立桥墩模型，按下式计算等效撞击力:

(3)

式中：d1为在作用点施加一个单位力求出的作用点处位移，d2为在作用点处施加撞击力和弯矩时程后求出的对应位移。

用这种方法计算出四种不同速度的等效静力为：Pd60=1.24 MN，Pd80=1.79 MN，Pd100=3.59 MN，Pd120= 5.10 MN。

2.4 脉冲简化法计算等效静力

根据Chopra[11]，将车撞桥墩简化成无阻尼体系，如图5所示。

图5 无阻尼单自由度体系

外荷载取矩形、半周正弦和三角形三种形式的脉冲荷载分别予以考虑，如图6所示。

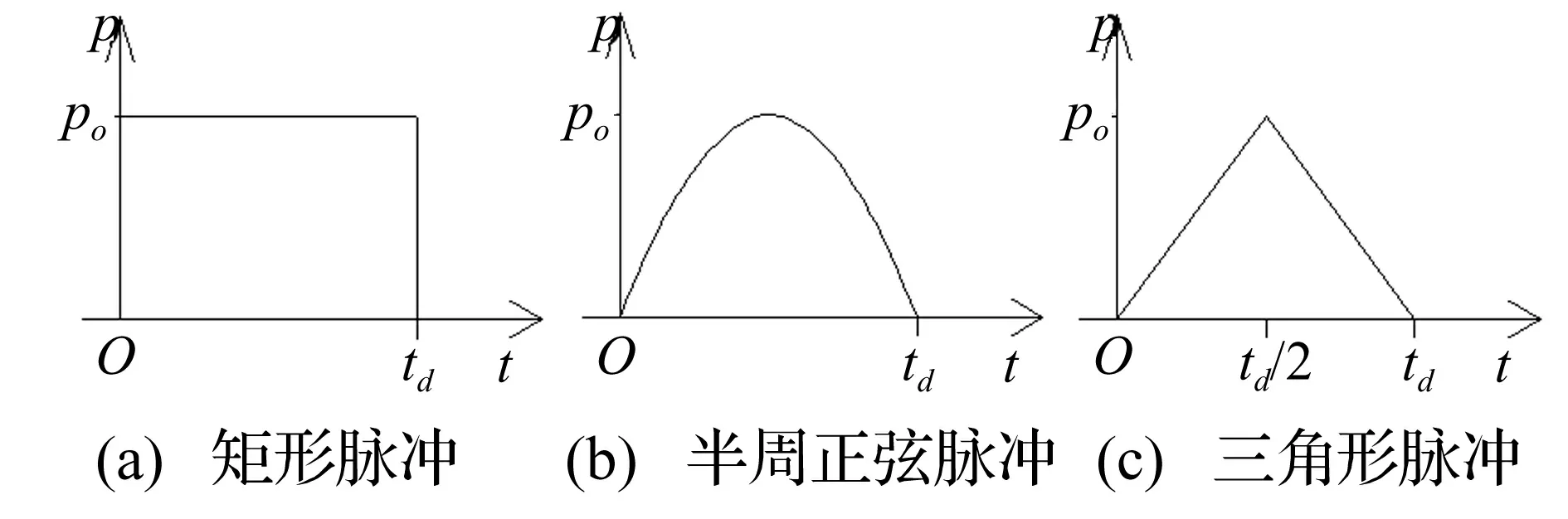
图6 几种脉冲荷载

不考虑阻尼时，体系动力学方程如下：

(4)

图7 对三种相同幅值脉冲力的冲击谱

对具有相同最大荷载值P0的三种脉冲(矩形、半周正弦和三角形)的冲击谱绘于图7中。如果脉冲持续时间td比Tn/2(半个周期)长，则总的最大变形发生在脉冲作用时间，因此脉冲形状非常重要；如果对于较大的td/Tn值，这时整体最大值受加载速度影响，比如突然从零增加到P0的矩形脉冲产生最大变形。

如果脉冲持续时间td比Tn/2短，则体系的整体最大反应发生在它的自由振动阶段，并受脉冲的时间积分控制，面积相同的三个脉冲力的冲击谱见图8。

图8 面积相同的三个脉冲力的冲击谱

针对这种情况，可以考虑td/Tn趋于零的极限情况来证明，随着脉冲持续时间与体系的固有周期相比变得非常短，脉冲变成纯冲量，其值可以表示为：

(5)

体系对这个冲击力的反应是无阻尼体系反应的单位脉冲响应乘以I，即：

(6)

最大变形为：

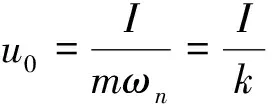
(7)

根据等效位移法定义，动力作用下体系产生u0位移，对应需要的静力Pa为：

(8)

汽车撞击桥梁过程，一般在0.2 s时结束，其中有效时间段不超过0.1 s，保守的取td=0.1 s，在图8中可以看出，在td1/2时，两个解答差别加大，不能再继续使用纯冲量解。也就是说，纯冲量解适应条件为td/Tn<1/2,即Tn>0.2 s。因此计算等效静力时，对于刚度较小的桥墩(f<5Hz)可以使用简化脉冲法，对于刚度较大(f>5 Hz)的桥墩要用等效位移法。

对于本算例，提取墩顶位移时程，做快速傅里叶变换(FFT)，得到桥墩频谱响应，如图9。

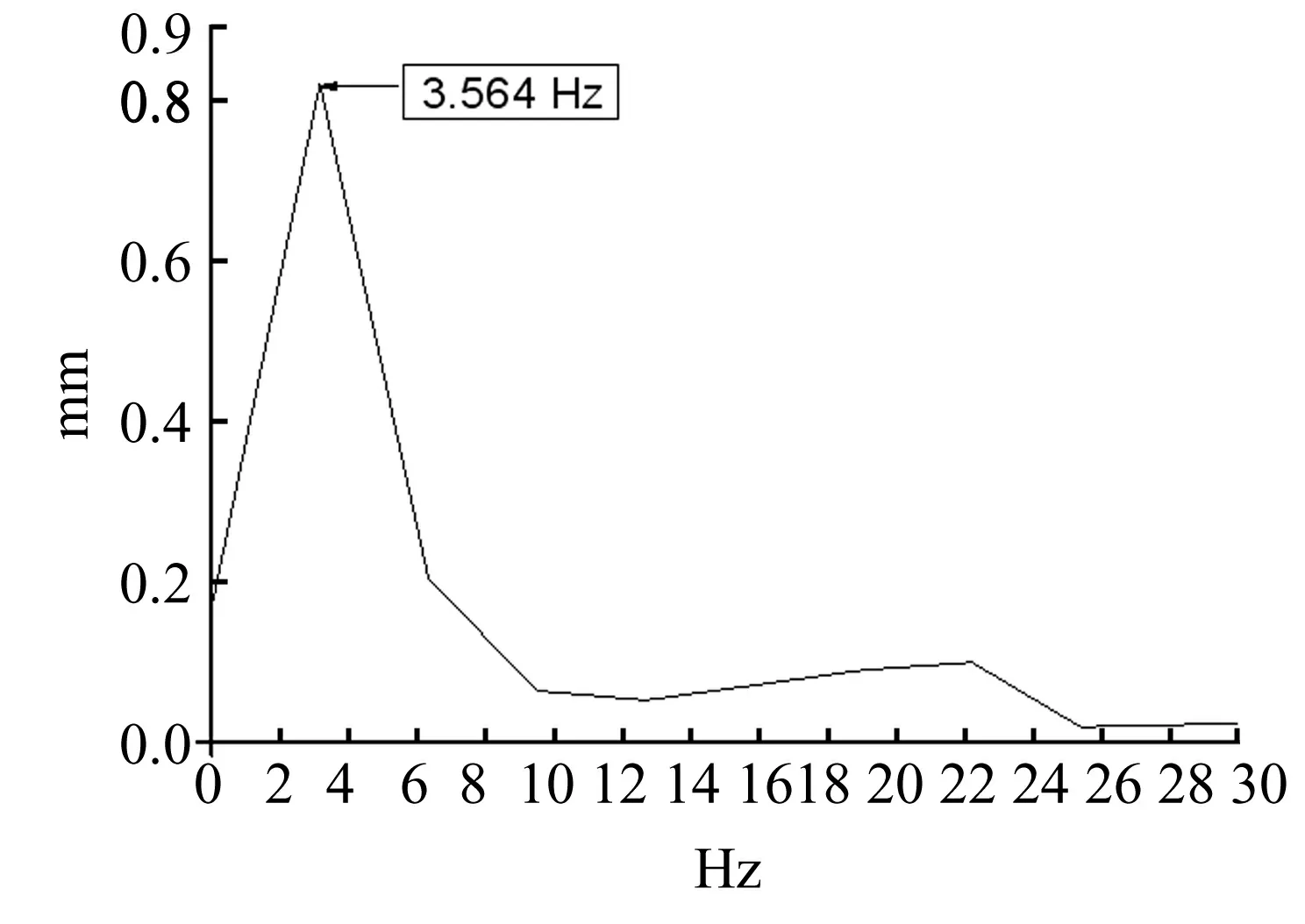
图9 频谱响应图

从图中可以看出，其响应峰值出现在一阶频率3.564 Hz处(用Ansys模态分析也得出了相同结果)。因此可采用简化脉冲法进行分析。

参照上述公式计算其等效静力为：Pa60=1.99 MN，Pa80=2.43 MN，Pa100=3.15 MN，Pa120= 4.37 MN。

2.6 四种计算方法结果对比

表1和图10汇总了上述四种方法的计算等效静力结果及峰值撞击力的比较。

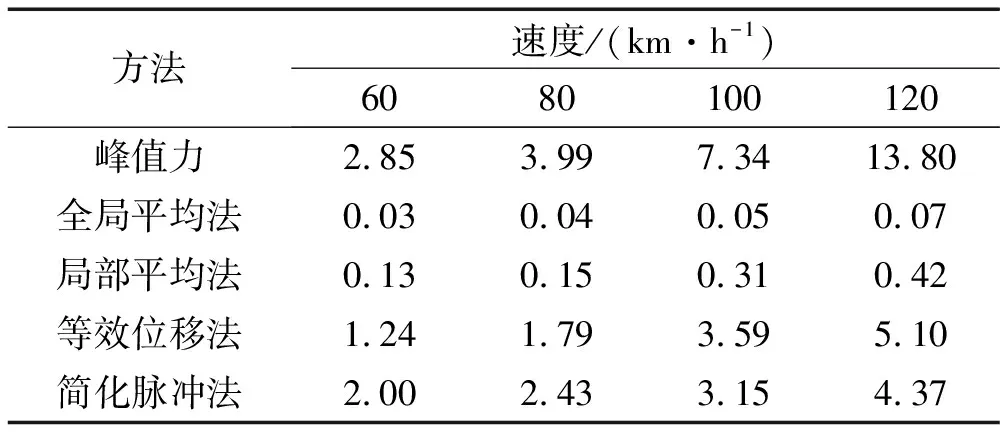
表1 四种等效静力方法计算结果的比较(单位：MN)

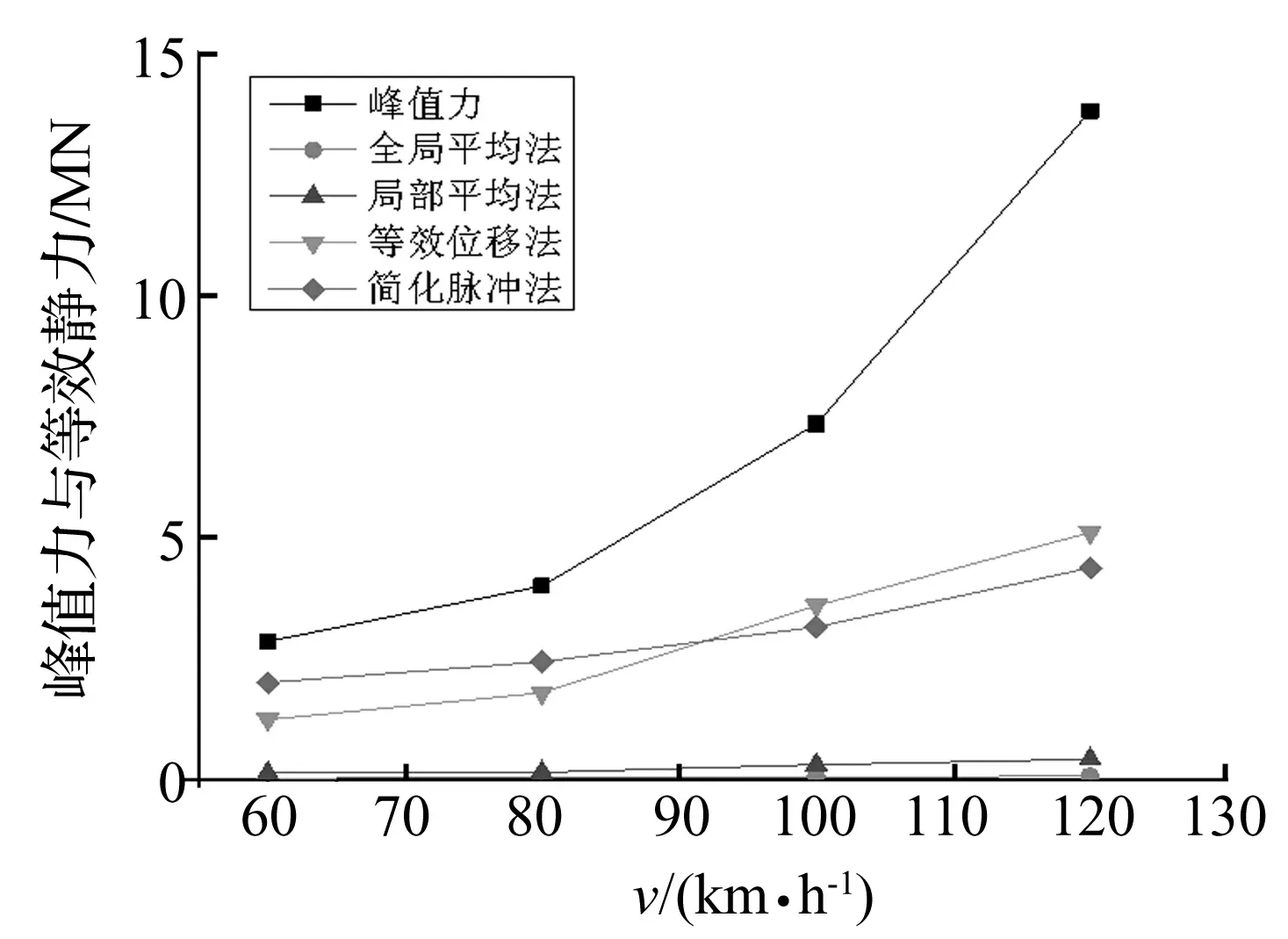
图10 峰值力与等效静力汇总图

从以上比较可以看出，尽管峰值撞击力很大，在120 km/h时达到13.8 MN，但因为撞击过程是瞬态的，峰值大约只有0.01 s，在0.2 s撞击过程所占时间很少，结构还没有来得及反应，过程已经结束，直接采用撞击力峰值作为碰撞过程控制力是不合理的，但文献[12]表明，峰值撞击力对桥上列车的运行安全影响很大。

全局平均法[4-5]，在船舶撞击桥墩计算等效静力中有一定参考价值，因为船舶撞击桥墩作用时间大约3～4 s，有一个持续的相对平缓的平台区域，然而汽车撞击桥梁过程中，虽然撞击力时程曲线中撞击力峰值很大，但是仅仅是一个尖峰，持续时间不到0.01 s，对应峰值时刻数据点少，总体平均出来等效静力过于偏小。因此，全局平均法计算车撞桥墩等效静力与实际匹配度较差。

局部平均法[4-5]，撞击力时程曲线中峰值附近虽然撞击力值很大，与全局平均法一个道理，仍然因为作用时间短，数据点少，平均出来等效静力偏小，不能很好表达真实等效撞击力大小，并且选取波峰或者波谷随机性太大，结果波动大。

等效位移法和简化脉冲法。根据结构动力学原理，td/Tn<1/2时，即Tn>0.2 s体系的整体最大反应发生在它的自由振动阶段，其解为受脉冲的时间积分控制的纯冲量解。因此频率f<5 Hz的柔性墩计算等效静力时可以使用简化脉冲法，频率超过5 Hz的桥墩要用等效位移法计算撞击力的等效静力。从图10可以看出，这两种方法的解答在1～5 MN之间，理论上计算是可行的，在没有实际足尺试验的情况下，这是计算车撞等效静力的有效途径。这两种方法的计算值都远超我国规范1 MN和美国规范1.8 MN的规定，说明规范限值偏小，下面我们将与既有工作比较对其准确性作进一步验证。

3 既有工作结果比较

Sherif EI-Tawil[13]采用55 km/h、90 km/h、110 km/h、135 km/h四种不同撞击速度正向撞击矩形和圆端型桥墩，给出了撞击力峰值和脉冲法算出的等效静力。为便于对比分析，本文忽略桥墩形状和尺寸影响，参照Sherif EI-Tawil论文参数选取，采用55 km/h、90 km/h、110 km/h、135 km/h四种不同速度撞击本文桥墩，撞击力时程如下：

1.55km/h，峰值2.75MN；2.90km/h，峰值4.97MN；3.110km/h，峰值10.60MN；4.135 km/h，峰值12.60MN

可以看出，Ford卡车在速度135 km/h时，撞击发生在0.09 s时，因为车厢的二次撞击，出现二个高达20.80 MN和21.30 MN的撞击力峰值。

用等效位移法和脉冲简化法计算数据结果与Sherif EI-Tawil[13]数据比较，假定其论文里面矩形墩(145 cm×137.5 cm×1 630 cm)为1号墩，圆柱形墩(直径107.5 cm，高度992.5 cm)为2号墩，本文模拟计算为3号墩(简化为200 cm×300 cm×21.34 cm，周期为0.280 6 s)，具体结果汇总见表2。

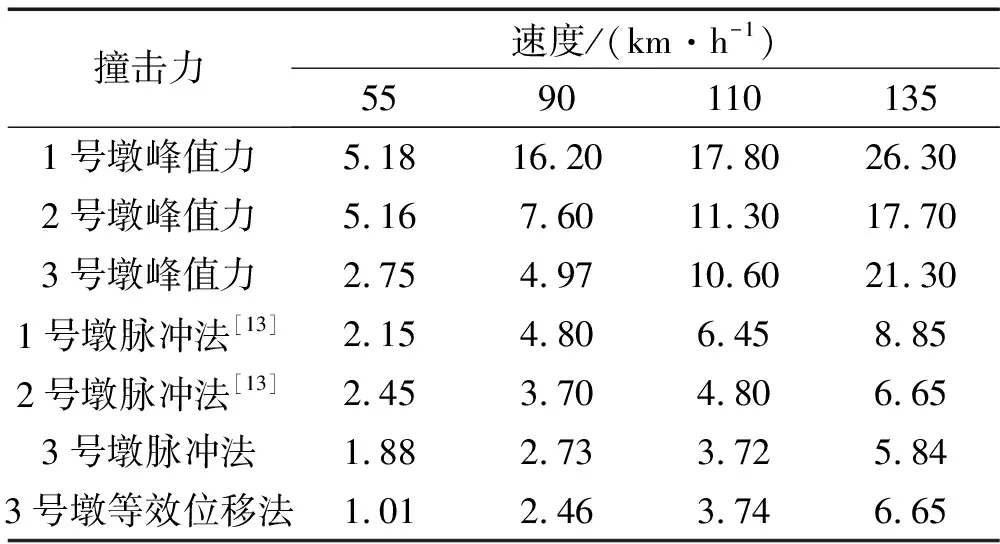
表2 与既有工作结果对比(单位：MN)

为了比较更直观，把所有等效静力值和规范限值绘于图12。图中，1号墩和2号墩等效静力是Sherif EI-Tawil计算的。

可以看出，1号墩等效静力曲线近似直线，本文脉冲法计算的3号墩等效静力与2号墩等效静力规律上接近一致，虽然桥墩尺寸不同，计算结果在量级上是一致的，在范围上也是比较接近的。同样是3号墩，采用等效位移法和脉冲法计算等效静力，计算结果在速度90～110 km/h期间是趋于一致的，在时速低于90 km/h时，等效位移法计算值偏小，时速大于110 km/h时，等效位移法计算值偏大。经过与既有工作比较，可以看出脉冲法和等效位移法在时速90～110 km/h，频率小于5 Hz的柔性桥墩计算结果趋近一致，具有较高可信度。对于大于频率大于5 Hz的桥墩，需要用等效位移法计算等效静力。

图12 等效静力汇总图

通过上述计算等效静力发现规范限值偏小，上述计算值在结构设计中能否直接使用有待进一步研究，但是也能提供一定参考价值。在动力问题研究中不能直接引用规范限值和上述计算静力值，本文建议取撞击力在时域内积分值作为动力研究的输入激励，因汽车撞击全程不超过0.2 s，远小于结构周期，激励波形形状不予考虑，撞击全程时间可以取0.05 s。

4 结 论

本文建立了8 t载重Ford卡车与苏州市某互通立交桥桥墩碰撞的精细有限元分析模型，采用ANSYS LS_DYNA碰撞分析软件计算得到了八种不同速度下汽车撞击力时程曲线。在此基础上提出了四种不同计算等效静力的方法，并与既有工作进行了比较，得出了以下结果和结论：

(1)给出了全局平均法、局部平均法、等效位移法、简化脉冲法4种车撞力的等效静力的定义和计算方法，使车撞等效静力的概念得到明确的诠释，可供桥梁车撞设计参考；

(2)将本文建议的车撞力计算方法结果与既有研究的计算数据进行了对比分析，说明了本文计算方法的合理性，也说明在原型和模型碰撞试验数据缺乏的情况下，碰撞有限元数值模拟技术是建立桥梁车撞力设计计算公式的可靠和有效的途径；

(3)简化脉冲法计算等效静力适用于频率在5 Hz以下的柔性桥墩，对频率大于5 Hz的桥墩，这种方法计算离散性增大，虽然可以粗略评估撞击力量级，但已经不够准确，要想获得更准确可靠地等效静力数据，可以采用等效位移法。

最后需要说明的是，桥梁车撞力受很多复杂因素的影响，本文初步探讨了汽车撞击力等效静力计算的基本方法，在条件允许的情况下应该进行模型或者足尺实验进一步验证其准确性。

参 考 文 献

[1]中华人民共和国行业标准.高速铁路设计规范(试行)(TB10621-2009)[S].北京：中国铁道出版社,2009.

[2]中华人民共和国铁道部.铁路桥涵设计基本规范(TB10002.1-99)[S].北京：中国铁道出版社，1999.

[3]AASHTO I.RFD.AASHTO LRFD bridge design specifications [S].Washington,D.C.1991.American Association of State Highway and Transportation Officials,2007.

[4]王君杰.桥梁船撞研究与工程应用[M]，北京：人民交通出版社，2011.

[5]王君杰，陈 诚，汪 宏，等.基于碰撞数值模拟的桥梁等效静力船撞力一基本公式[J].公路交通技术,2009,4(2):66-70.

WANG Jun-jie,CHEN Cheng,WANG Hong,et al.Equivalent static force of ship impact to bridge based on impact numeric simulation-fundamental formula[J].Technology of Highway and Transport,2009,4(2):66-70.

[6]Derucher K N.Analysis of concrete bridge piers for vessel impact [C].Proc.of Sino-America Symposium on Bridge and Structural Engineering,1982: 1-11.

[7]Thilakarathna H M I,Thambiratnam D P,Dhanasekar M,Perera N.Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment [J].International Journal of Impact Engineering,2010,37(11): 1100-1112.

[8]Buth C E,et al.Analysis of large truck collision with bridge.http://tti.tamu.edu/documents/9-4973-1.pdf,2010.

[9]陆新征，何水涛，黄盛楠.超高车辆撞击桥梁上部结构研究[M].北京：中国建筑工业出版社，2011.

[10]Xu L J,Lu X Z,Smith,S T,et al.Scaled model test for collision between over-height truck and bridge superstructure[J].International Journal of Impact Engineering,2012,49: 31-42.

[11]Chopra A K.Dynamic of structures: Theory and applications to earthquake engineering,2ndEd.Prentice-Hall,Englewood Cliffs,N.J.,2001.

[12]Xia C Y,Lei J Q,Zhang N,et al.Dynamic analysis of a coupled high-speed train and bridge system subjected to collision load[J].Journal of Sound and Vibration,2012,331(10): 2334-2347.

[13]Sherif EI-Tawil P E M,ASCE,et al.Vehicle collision with piers [J].Journal of Bridge Engineering,2005,10(3): 345-353.

[14]中华人民共和国铁道部.铁路桥涵设计基本规范(TB10002.1-99)[S].北京：中国铁道出版社，1999.