基于模型预测控制的高速柔性并联机构振动控制

胡俊峰， 张宪民， 徐贵阳

(1. 江西理工大学 机电工程学院，江西 赣州 341000; 2. 华南理工大学 机械与汽车工程学院, 广州 510640)

并联机构具有高速、高精、高承载能力等特点，在许多领域得到应用。为实现并联机构的高速精密运行，必须考虑其构件变形，对其进行振动控制。柔性并联机构为分布参数的非线性、时变、多输入多输出系统，这给振动控制带来较大困难。由于压电陶瓷等智能材料和现代控制理论的发展，采用智能材料作传感器和作动器的振动主动控制得到了应用[1-6]。

但由于柔性并联机构的非线性因素、各参数之间的耦合、模型参数的不确定性和时变性等影响，很难精确建立系统的数学模型，这给其振动主动控制带来困难。模型预测控制具有以下基本特征：模型预测、滚动优化和反馈校正。模型预测控制方法对系统模型要求低且形式灵活，能够实时补偿因系统参数时变和非线性因素等引起的控制误差，有效克服系统不确定因素的影响，控制效果好且鲁棒性强。

本文以一种考虑构件的弹性变形的新型两自由度平动并联机构为研究对象，采用有限元法和实验模态方法建立其离散状态空间模型，研究应用模型预测控制策略设计鲁棒振动控制器。

1 系统动力学模型

应用有限元法，建立含有压电陶瓷的柔性并联机构的弹性动力学方程[3-4]

(1)

采用模态技术处理，忽略高阶模态的影响，引入变换

U=ψηc

(2)

其中，ψ为振型矩阵，ηc为受控模态的振型坐标，将式(2)代入式(1)可得：

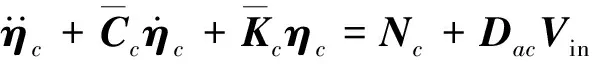
(3)

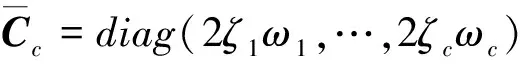
(4)

其中，ω1,…,ωc为系统前c阶固有频率，ζ1,…,ζc为系统前c阶阻尼比，Dac、Das分别为系统作动器、传感器分布矩阵，它们是与作动器、传感器位置和模态振型有关，Nc为在模态坐标下的广义力，称为模态力。

定义受控状态变量为

(5)

则式(4)可以写成状态空间方程形式

(6)

式中，

(7)

2 模型预测控制器设计

模型预测控制结构如图1所示。在模型预测控制中，将系统输出的动态预估问题分为预测模型的输出预测和基于偏差的预测校正两部分。式(6)所表示的预测模型只是对柔性并联机构动态特性的粗略描述，而实际系统中存在非线性、时变性和随机干扰等因素，因此，预测模型不可能与实际对象完全相符，预测模型的输出与实际系统输出之间必然存在偏差。采用这种偏差进行在线校正，使系统构成具有负反馈环节的系统，从而提高预测控制系统的鲁棒性，以满足柔性并联机构的鲁棒振动控制。

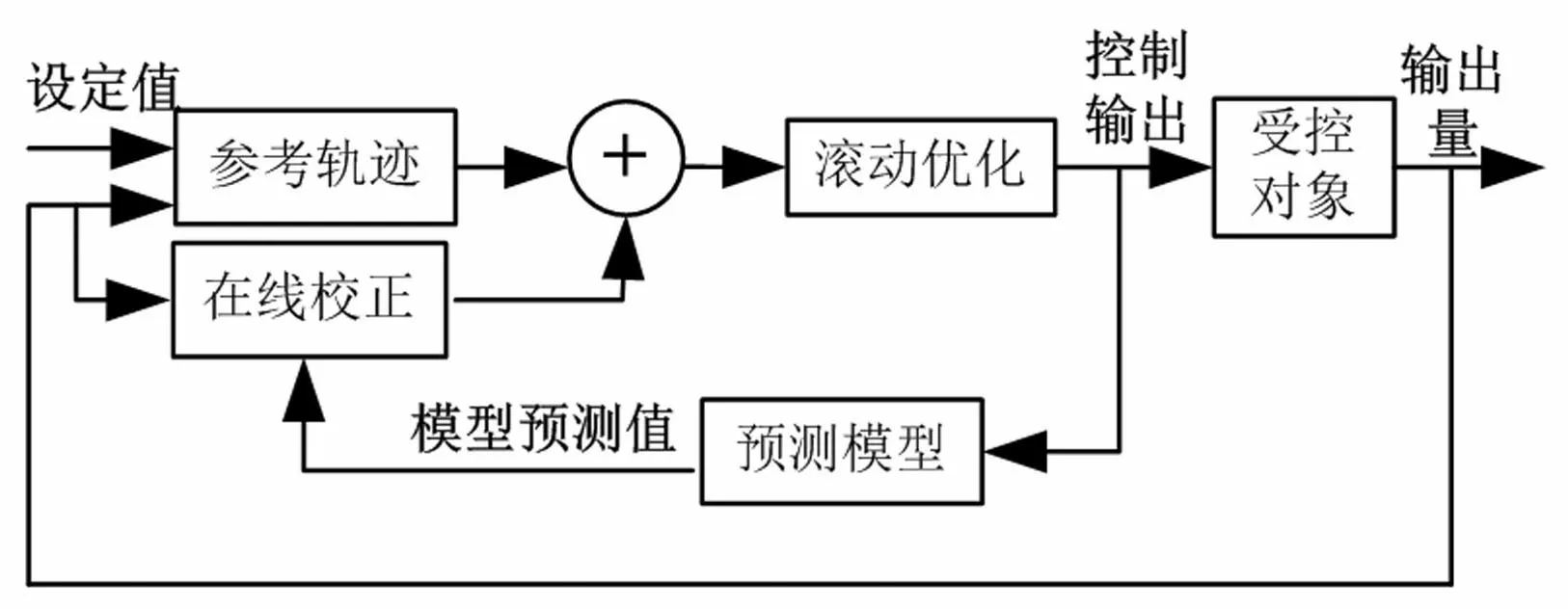
图1 模型预测控制结构

2.1 系统的预测模型

由于模型预测控制是基于离散状态方程进行预测，并且采用计算机进行控制，能方便存取各时刻的采样信号，便于计算。首先对系统连续状态方程(6)进行离散化，离散控制状态方程可写成如下形式：

(8)

式中，设采样周期为Ts，k表示kTs时刻，Ψ(k)、Γ(k)、Θ(k)、Ω(k)分别表示由连续状态方程转换为离散状态方程系数矩阵，Nc(k)为不可测扰动，并且考虑测量噪声对输出的影响，则测量输出ym(k)为

ym(k)=Ω(k)Xc(k)+m(k)

(9)

其中，m(k)为测量噪声。不可测量干扰Nc(k)的状态空间模型为

(10)

(11)

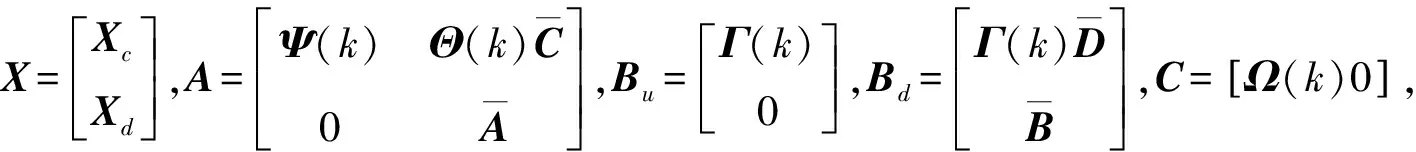
X(k+1)=AX(k)+BuVin+Bdnd(k)
y(k)=CX(k)+Ddnd(k)

(12)

为了求解预测控制问题，在状态空间表达式中必须计算被控变量的预测值。它可由当前状态的最佳估计值以及假设的未来输入计算，或等价地可由最近的输入V(k-1)的值以及假设的未来输入变化ΔV(k+i|k)来计算。为了表述简单，假设从时刻k=0开始，根据式(12)可以预测模型的未来输出值，第i个时间步的输出可以表达为：

(13)

其中，p为预测时域，i代表预测时域p的第i时间步，h为控制时域。式(13)也可以写成如下形式

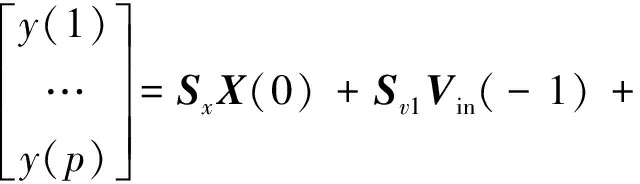
(14)

其中，

(15)

(16)

2.2 状态估计器设计

由于状态变量为模态位移和模态速度，它们是不能测量的，所以需要用一个状态估计器估计这些状态量。状态估计器是基于如图2所示的模型建立的，状态估计器是为了估计受控对象、输入干扰对象的状态，使用卡尔曼滤波器技术设计。状态估计量可表示为：

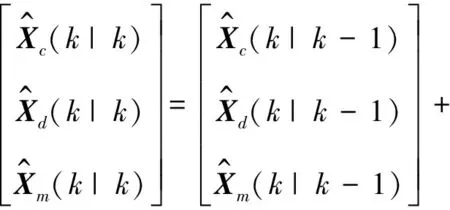
(17)

(19)

2.3 滚动优化

模型预测控制可以通过解下面的优化问题得到，设预测控制最优化目标函数为：

minJ(ΔV)

(20)

其中，J为系统性能指标，它可以表示为：

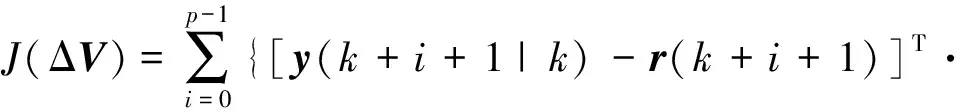
Vtarget(k+i)]TRV[V(k+i|k)-Vtarget(k+i)]}(21)

其中，ΔV为设计变量，它可以表示为ΔV=[ΔV(0),…,ΔV(p-1)]T，Q是ny×ny矩阵，RΔV和RV分别是惩罚是设计变量和控制输入电压的系数矩阵，它们是Na×Na矩阵，它们均为半正定矩阵，Na为作动器的个数，矩阵Q用于惩罚被控输出的预测值y(k+i+1|k)与传感器期望输出r(k+i+1)之间的偏差，Vtarget(k+i)是控制输入电压设定值。

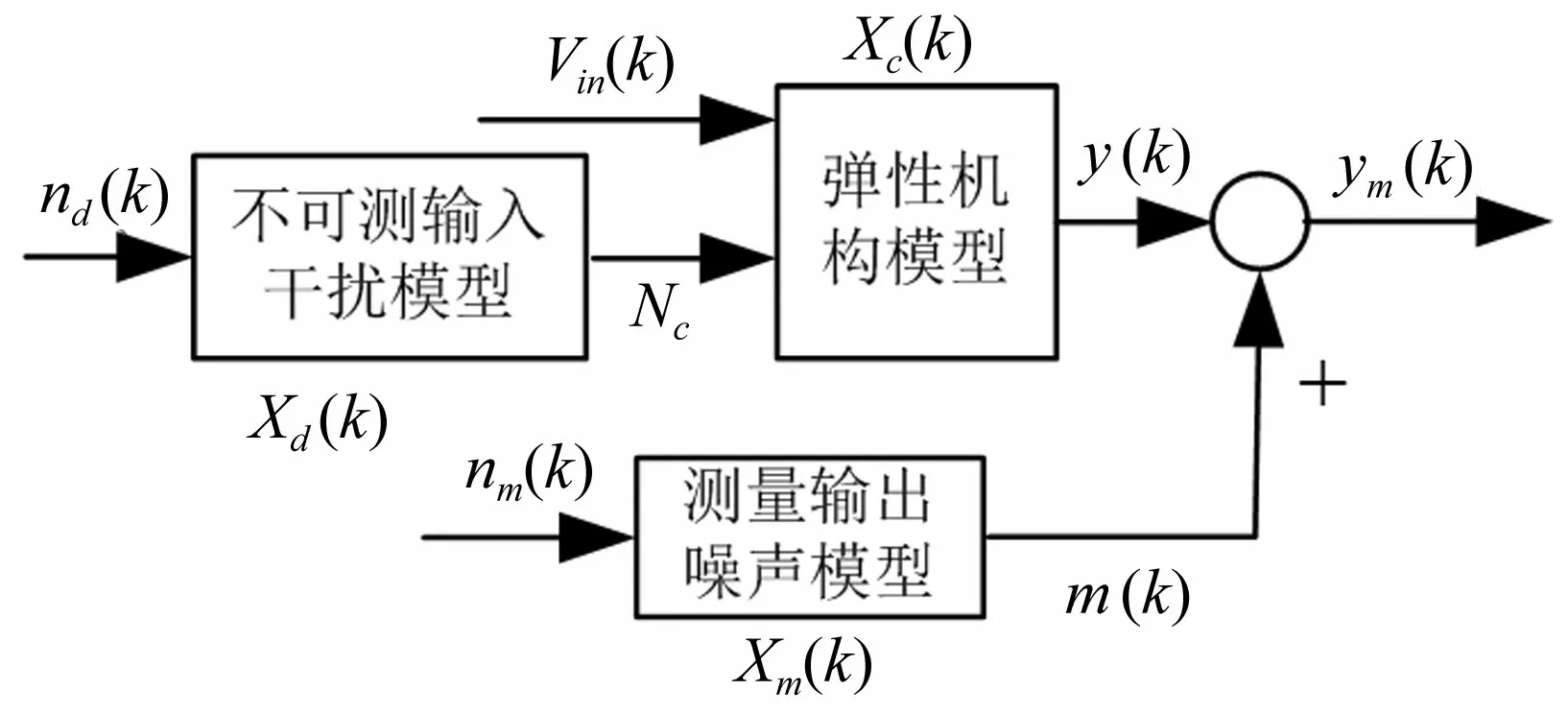
图2 用于状态估计的模型

受控系统存在的约束有控制电压及其变化率的约束条件和系统输出量约束条件：

Vjmin(i)≤Vj(k+i|k)≤Vjmax(i)
ΔVjmin(i)≤ΔVj(k+i|k)≤ΔVjmax(i)
yjmin(i)≤yj(k+i|k)≤yjmax(i)

(22)

其中，下标( )j表示向量的第j个分量，(k+i|k)表示基于时刻k的值的时刻k+i的预测值，r(k)是输出参考值。

将式(21)展开可以表达为如下形式：

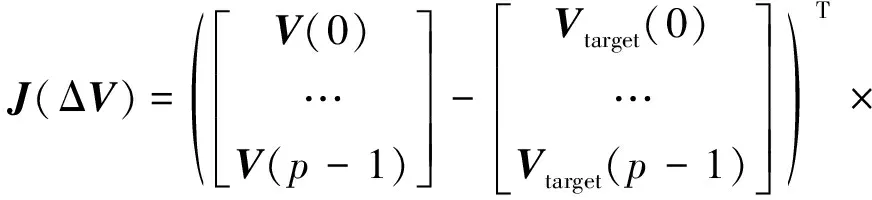
(23)

WV=blkdiag(RV,…,RV)
WΔV=blkdiag(RΔV,…,RΔV)
Wy=blkdiag(Q,…,Q)

(24)

式中,blkdiag(·)代表块对角矩阵，每一个矩阵的块重复p次。

由于控制输入信号V(k)与未来输入变化ΔV(k)的关系可以表示为：

V(k)=V(k-1)+ΔV(k)

(25)

将式(14)代入式(23)，则最终优化目标函数可以写成如下形式：

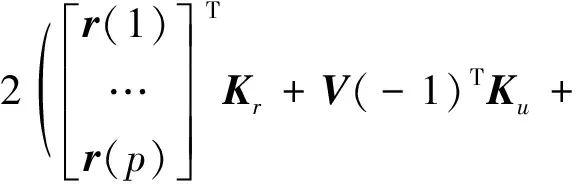
(26)

式中，Const表示常数，KΔV、Kr、Ku、KVt和KX分别为目标函数的系数矩阵。

同理，约束条件(22)也可写成如下形式：

(27)

将式(14)和式(25)代入上式，约束条件可以写成如下形式：

MΔVΔV≤Mlim+MVV(-1)+MXX(0)

(28)

式中，MΔV、Mlim、MV、MX为约束条件系数矩阵，它们可以根据约束条件的上下边界获得。

联合式(26)和式(28)的最优化问题即是一个二次规划优化问题，利用二次规划方法求解可以得到ΔV的最优解ΔV*，它可以表示为：

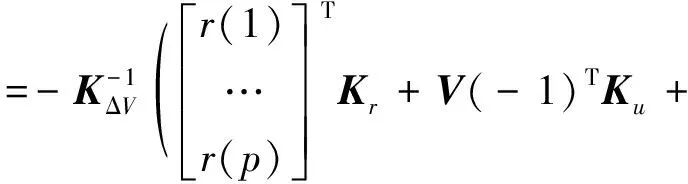
(29)

3 作动器与传感器位置优化

由于振动响应的控制和测量大多采用离散分布式的作动器/传感器，它们在机构上的位置和数目优化问题对系统可控性/可观性有很大影响。合理的作动器布置可以在较小输入能耗作用下最大限度的抑制振动，否则可能使系统性能恶化，甚至导致系统不稳定。相应地，不合理的传感器配置，可能导致无法对系统性能做出正确的评定。

作动器/传感器位置优化的目的是通过合理选取作动器的位置和数目以确定作动力分布矩阵，从而尽可能大地影响被控模态，以及合理的选取传感器的位置和数目以确定传感器的输出系数向量，使得传感器测量的响应中尽可能多包含各阶的模态分量，同时应能保证闭环控制系统的性能稳定。由于现有的位置优化准则过于复杂，采用一种表征作动能量的可控性指标和表征观测信号能量的可观性指标，以确定作动器和传感器的最优位置。

3.1 确定作动器位置

压电作动器作动力列向量可表示为[10]

fc=BcVin

(30)

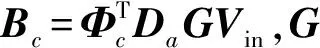
(31)

对作动力系数矩阵Bc进行奇异值分解可得

Bc=USaVT

(32)

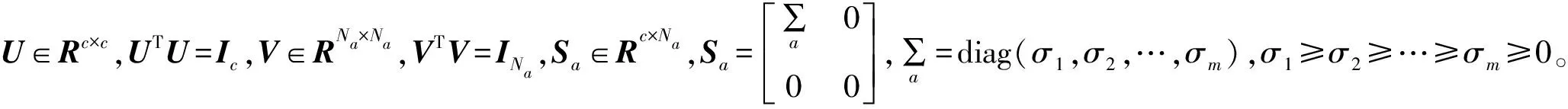
将式(32)代入式(31)可得：

(33)

设Vineq=VTVin，由于VTV=INa，则

(34)

如果控制输入电压Vin给定，向量Vineq的值也可确定，即

(35)

基于σi在式(35)所示控制能量中的作用，引入可控性指标

(36)

由式(36)可知，控制电压确定后，指标Ωa正比于作动器提供的能量，指标Ω值越大，作动器提供的能量越大，而作动能量又与分布矩阵Da、模态矩阵有关。因此，对于给定的控制输入电压，根据Ωa值的大小可以确定作动器的位置，Ωa值最大的位置即为放置作动器的最优位置。

3.2 确定传感器位置

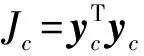
(37)

同理，对系数矩阵Cc进行奇异值分解，则性能指标Jc可表示为

(38)

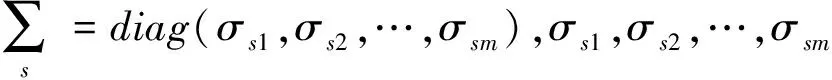
(39)

4 实 例

为了验证所设计的控制器的有效性，对一新型2自由度并联机构进行振动主动控制研究。考虑到高速机构振动控制的复杂性，对机构进行了简化，并为了简化模型，设计如图3所示的并联机构[7-8]，其简图和系统坐标系统如图4所示。l1和l2分别为主动臂和从动臂的长度，l1=505 mm，l2=430 mm。由于从动臂相对于主动臂为细长杆件，为了研究方便，将机构的主动臂视为刚性构件，从动臂为柔性构件。板条由铝合金制成，长360 mm，宽60 mm，厚2 每一柔性从动臂用梁单元进行模拟。系统单元划分如图5所示，图中Ni(i=1～21)为结点编号，Ej(j=1～20)为单元编号，从动臂 1、2均划分为10单元，系统共划分为20个梁单元，考虑边界约束，系统共有79个广义坐标。系统广义坐标U是在如图5所示的坐标系统XOY定义的，系统广义坐标为结点自由度，每个结点具有纵向位移、横向位移、弹性转角和曲率4个自由度，具体的有限元模型建立过程参见文献[9]。

4.1 作动器与传感器位置

设每个柔性杆粘贴3个压电作动器，对机构前4阶模态进行控制，并且作动器的尺寸已确定。下面确定放置作动器最佳位置。如图4所示，综合考虑弹性构件的长度和作动器不能重叠，设作动器位置为下面4种组合，第1种组合为分别作用在单元3、5、7、13、15、17；第2种组合为作用在单元3、5、8、13、15、18；第3种为3、6、8、13、16、18；第4种为4、6、8、14、16、18；作动器在4 种不同位置的性能指标如图6所示，它们分别为64.775 2、103.209 0、 93.635 4、82.081 9。由此可知，第2种组合的可控性指标最大，所以选择该组合，即作动器放置在如图8所示的单元E3、E5、E8、E13、E15、E18上。

对放置传感器的位置进行20种组合，对应这20种组合的性能指标值如图7所示，从该图可以发现第7种和第18种组合，性能指标值较大，这两种组合放置传感器的位置单元分别为单元3、5、8、13、15、18和单元5、6、8、15、16、18，恰好其中第7种组合为放置作动器的位置，而第18组合也有两个位置是放置作动器的位置，所以作动器和传感器采用同位配置较好。A1～A3表示对应于放置在单元E3、E5和E8的作动器，S1～S3表示放置在在单元E3、E5和E8中点的传感器。同样，A4～A6表示为放置在从动臂2上的作动器，对应于放置在如图所示的单元E13、E15和E18，S4～S6表示为放置在从动臂2上的传感器，对应于放置在单元E13、E15和E18中点。根据作动器的位置，并且考虑压电陶瓷片的长度为50 mm，为方便建模，设每一片压电陶瓷片放置位置为一梁单元，这样每一片压电陶瓷片施加在构件的力矩可视为加在单元节点上外力矩，可以设置每根从动臂10个单元的长度分别为65 mm、15 mm、50 mm、40 mm、50 mm、40 mm、40 mm、50 mm、15 mm、65 mm。

图3 实验配置

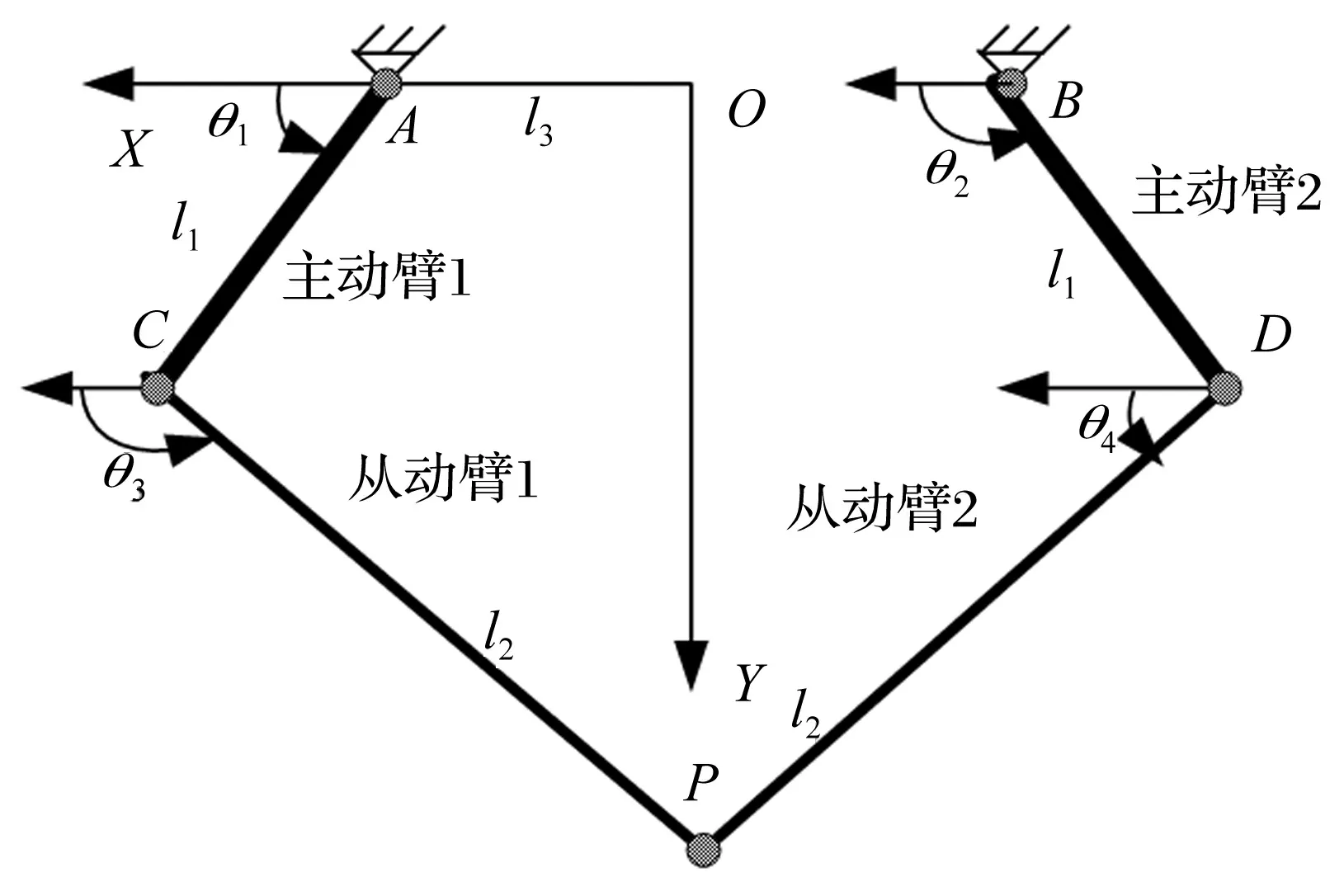
图4 机构简图及其坐标系统

图5 系统单元划分

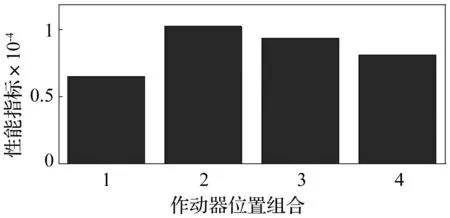
图6 作动器位于不同位置的性能指标值

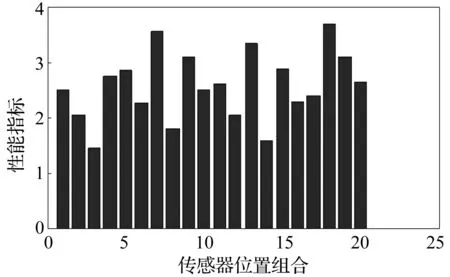
图7 传感器位于不同位置的性能指标值

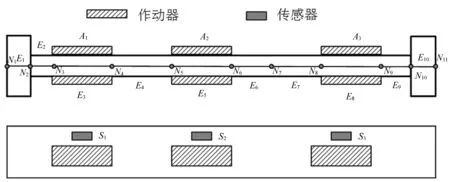
图8 作动器与传感器位置

4.2 实验模态测试

由于机构的阻尼比难以通过有限元方法获得，需要借助试验模态测试得到。采用脉冲锤击法进行实验模态测试。用力锤对机构进行敲击，产生一个宽频带的激励，如图9所示，固定敲击位置，测量12个不同位置的加速度信号。力锤是由PCB公司生产，型号为Model 086C03，测量范围为0～500 lbf，灵敏度系数为2.44 mV/N。加速度传感器采用Kistler 8690C50型压电式加速度计，它可以测量垂直于测量点的加速度信号。为了消除噪声干扰，采用多次平均，设每个测点的测量的次数为5次。使用ZonicBook/618E得到激励点和各测量点的时间历程数据，利用eZ-Analyst软件求出各测点的频响函数。采用ME’scopeVES对这些频响数据进行曲线拟合，得到拟合后的频响曲线如图10所示，得到系统的固有频率和阻尼比。

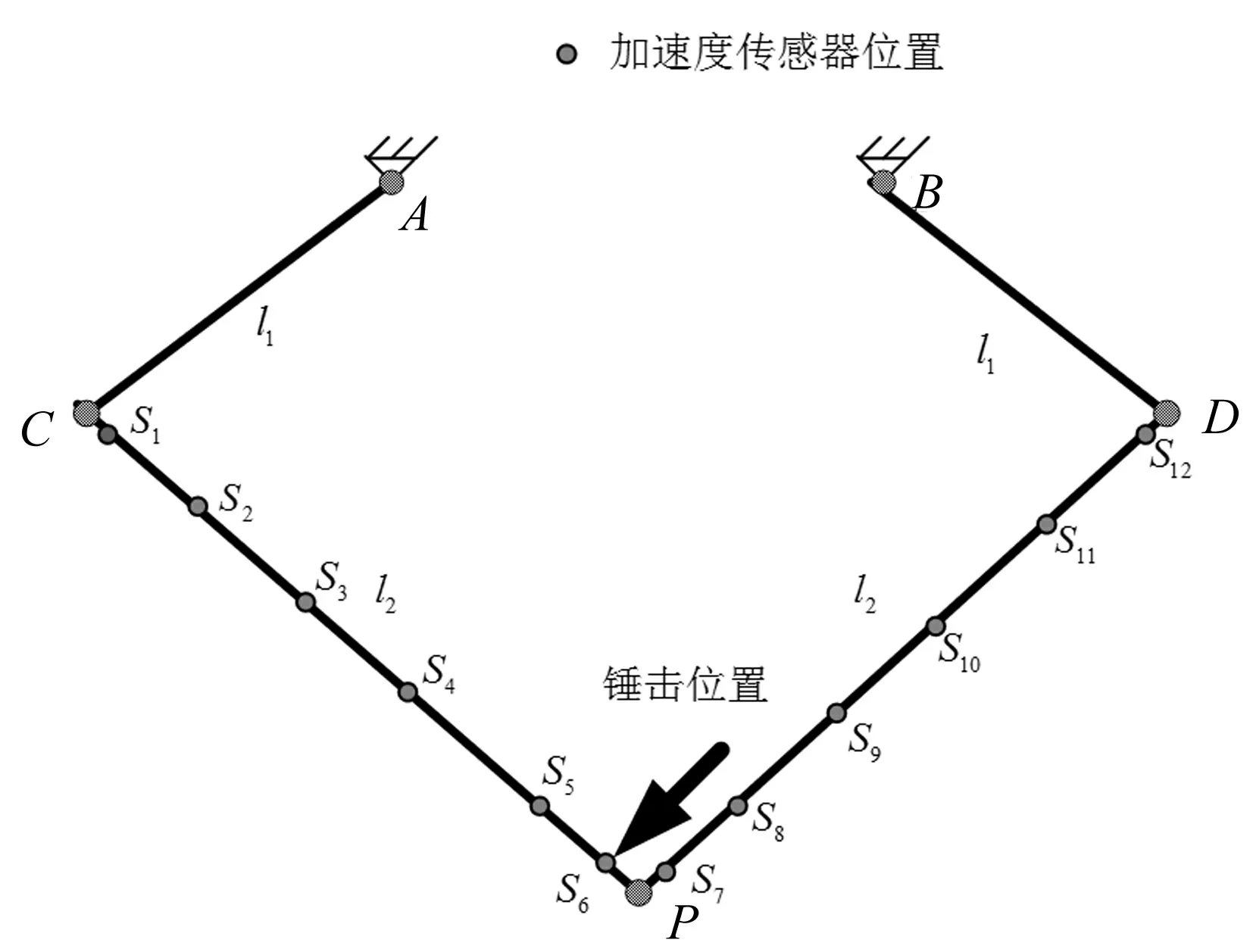
图9 加速度传感器布置

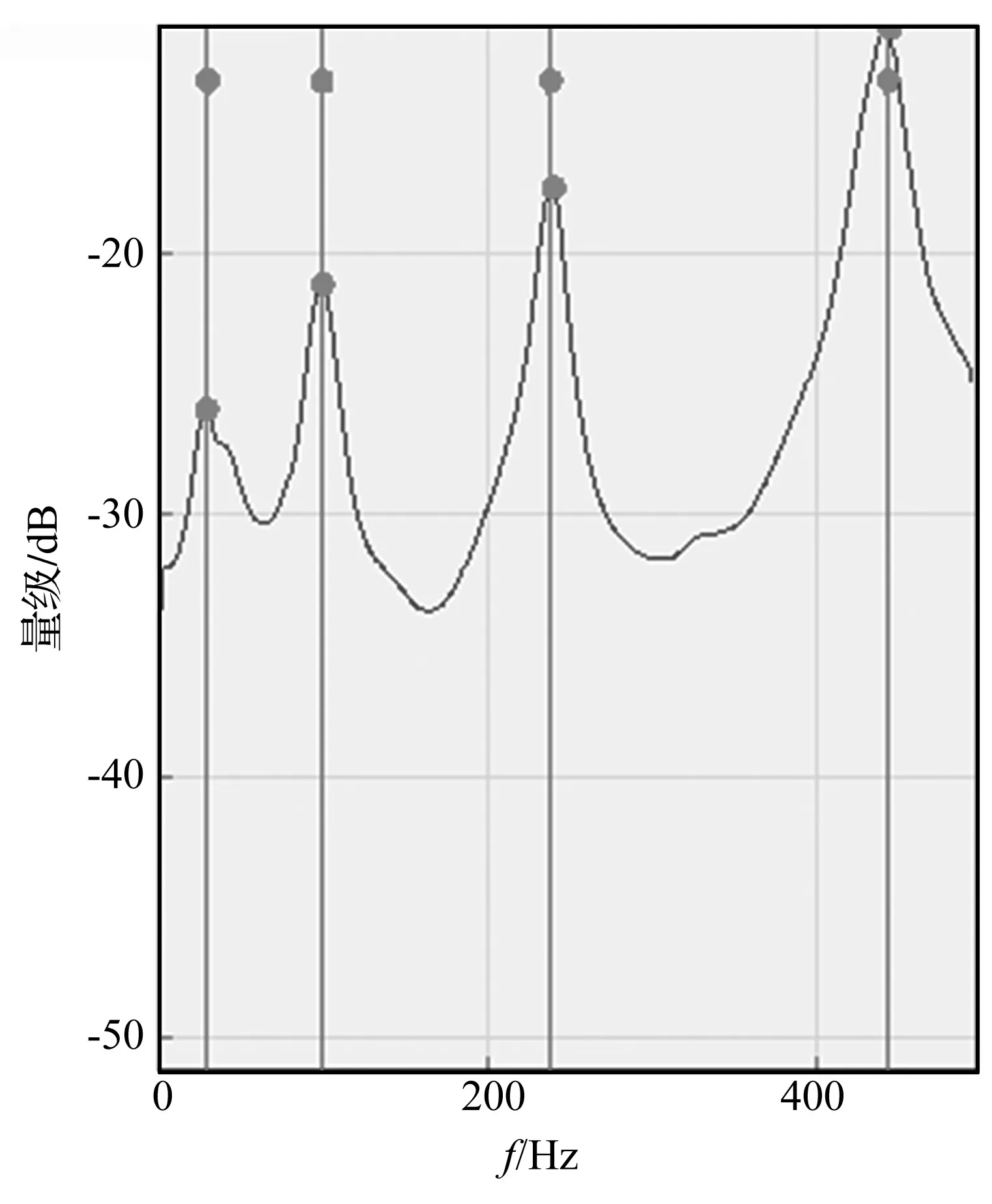
图10 频响拟合曲线

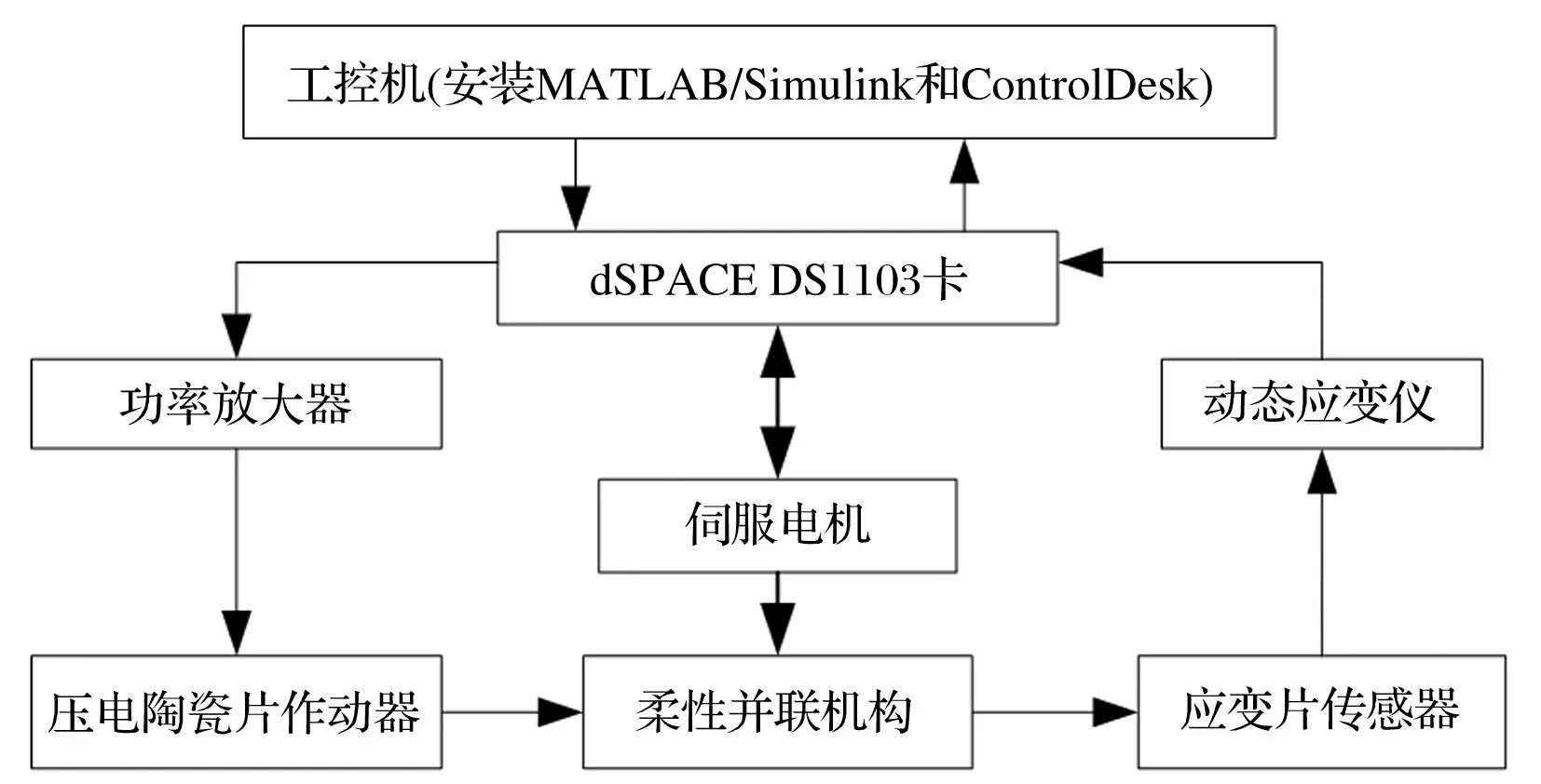
图11 振动控制试验原理图

由试验得到的前2阶固有频率、阻尼比和有限元计算得出的固有频率如表1所示，从该表可以看出，有限元计算值和实验值相对误差接近于13-19%，则说明采用有限元建立的模型和实际系统还存在一定的差距。造成这一误差的原因主要有以下几点：①机构在铰链处的约束复杂；②机构在铰链处存在间隙；③有限元方法采用梁单元，简化对实际构件模型的建立；④建立模型时没有考虑螺栓和螺母之类的构件。所以，应用于控制器设计的模型和实际系统存在误差，也就是说，理论模型不精确。

4.3 实验验证

为了实现机构的高速运动，采用伺服电机驱动控制对象，机构的刚体运动轨迹规划参见文献[8]。交流伺服电机型号为Panasonic MHMD042P1V，其配套的伺服驱动器型号为MBDDT2210003。机构是在高速的运动过程中执行操作，它的两个关节的角速度和角加速度都较高，图12(a)、(b)是以操作时间最短为目标，对机械手的关节空间进行最优运动轨迹规划得到的两个主动关节的角速度和角加速度，它们最大值分别接近15 rad/s、555 rad/s2。

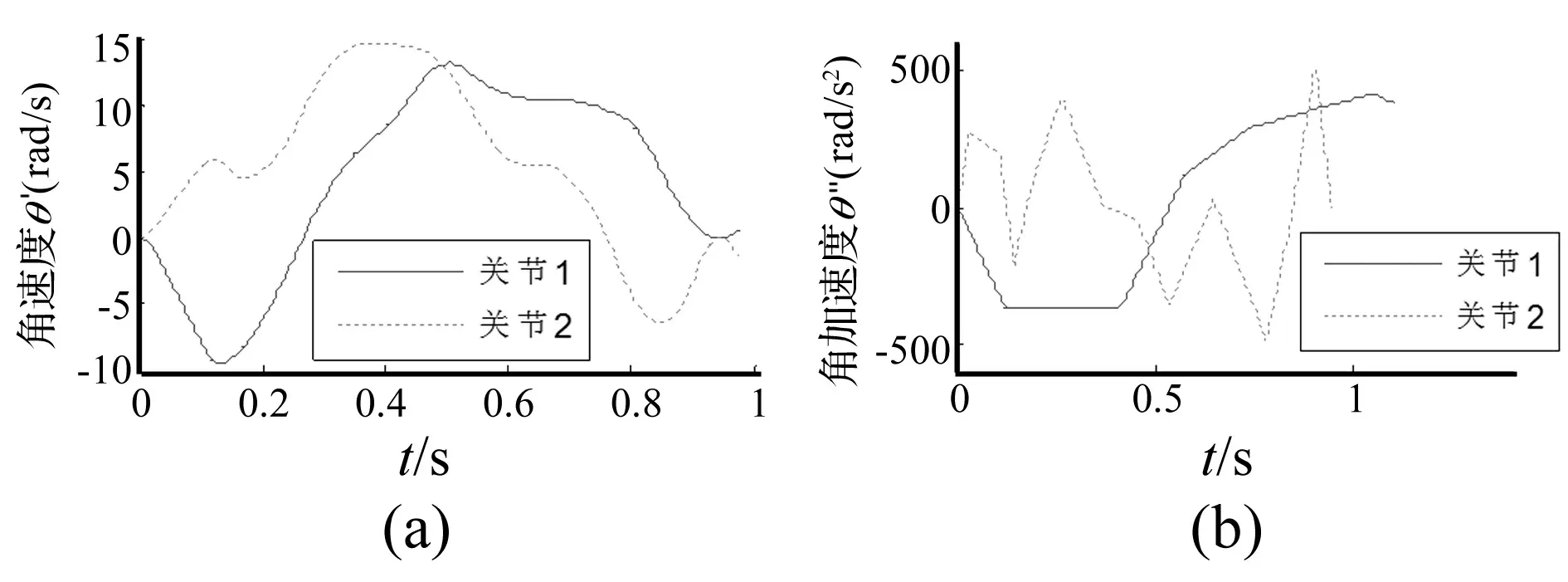
图12 关节角速度和角加速度

电阻应变计为由中航电测公司生产型号为温度自补偿型BE120-3AA(11)，该电阻应变计标称阻值为120 Ω，灵敏度系数为2.17。动态信号采集系统为ZonicBook/618E，8通道动态信号输入，每通道分辨率为16-bit，最大采样率1 MHz。功率放大器是由哈尔滨芯明天科技公司生产，型号为X-505.00，放大倍数为15，由于实验使用了6对压电陶瓷片，采用6路功率放大器分别驱动。dSPACE实时仿真系统是由德国dSPACE公司开发的一套基于MATLAB/Simulink的控制系统开发及半实物仿真的软硬件工作平台。本试验使用dSPACE DS1103平台和MATLAB/Simulink搭建振动控制系统。振动控制试验原理如图11所示，电阻应变片与动态电阻应变仪通过1/4桥路连接，应变仪将被测点的应变信号转换成电压信号传送至数据采集卡，采集到的数据以实时方式传送给dSPACE DS1103处理，按照所设计的控制器实时计算所需的控制电压，实时计算得到的数字量经过数模转换模块输出，由于D/A转换模块输出电压范围为-10～+10 V，需经电压放大器放大后施加给压电陶瓷片，完成对系统的控制。实时控制系统设计过程为：首先利用MATLAB/Simulink构建控制系统框图；然后，利用Real-Time Workshop技术将Simulink框图程序生成实时代码并下载到dSPACE快速原型机中；最后，使用dSPACE提供的综合试验与测试环境软件ControlDesk实现试验过程控制和参数在线修改和实时数据采集。为了实现机构高速运动过程中的实时振动控制，采用如图11所示的工作原理，通过dSPACE同时接受来自伺服电机和应变片传感器的信号，并根据该信号进行运动控制和振动控制，通过所设计的控制器同时发出刚体运动控制信号和振动控制信号，这样，机构高速运动控制与振动控制就能实现同步，以满足振动控制的实时性要求。

在不精确的理论模型的基础上应用鲁棒模型预测控制设计振动控制器。在设计控制器中，模态力视为白噪声信号，其幅值同样分别设为20.5、20.4。量测噪声设为幅值为6×10-6的白噪声。为了与实时控制采样周期相同，设模型预测控制器的采样周期Ts=0.001 s，预测时域p=8，控制时域h=2，加权矩阵为Q=diag(105,105,105,105,105,105)，Vtarget(k)=0，RV=0，RΔV=diag(0.01,0.01,0.01,0.01,0.01,0.01)，为了减小机构振动响应，应变片传感器期望输出r(k)=0，约束条件为控制输入电压的允许最小和最大值，即Vmin(k)=-150V，Vmax(k)=150V，控制输入电压在一个时间步的最小和最大变化率设为ΔVmin(k)=-300V/Ts，Vmax(k)=300V/Ts。

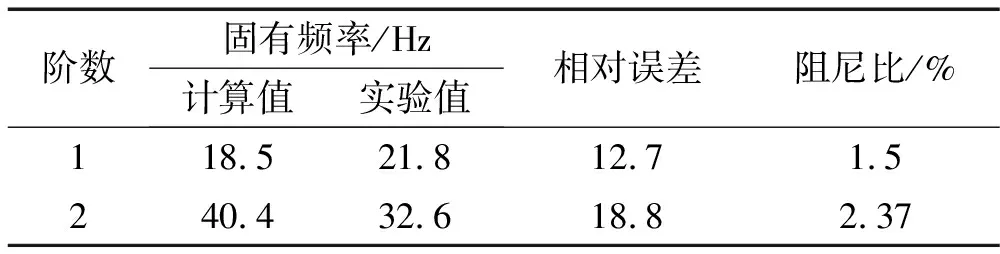
表1 系统固有频率和阻尼比

图13 在无控制和有控制两种情况下传感器S1～S6的输出应变

图13(a)、(b)、(c)、(d)、(e)、(f)分别为在无控制和有控制两种情况下传感器S1～S6的输出应变，分别比较6个传感器的输出应变变化，可以得知，在模型预测控制器作用下，传感器的输出应变以较快的速度衰减，也就是说，并联机构的弹性振动响应得到较大的抑制，这说明控制器的有效性和鲁棒性。图14(a)、(b)、(c)、(d)、(e)、(f)分别为在模型预测控制器作用下六个作动器的输入电压。由于模型预测控制器是基于离散状态方程模型设计的，控制器的输出电压为离散值，控制器的输出电压如图14所示，从该图可以看出，控制输入电压均满足约束条件，同样说明在允许的控制输入电压下，所设计的控制器能获得较好的性能。控制电压在大部分时间步均达到了约束条件的边界，说明控制器需要消耗较多的能量才能达到预期的控制效果。

图14 六个作动器的输入电压

5 结 论

考虑高速柔性并联机构的非线性和不确定性，采用模型预测控制理论设计控制器抑制其弹性振动响应。根据系统不精确的理论模型推导系统的预测模型。将不确定性外部扰动和量测噪声视为白噪声，采用Kalman滤波估计器估计系统状态变量，以控制电压及其变化率为约束条件，将系统性能指标和约束条件化为一个标准二次规划优化问题，通过求解这一优化问题来得到最优控制输出。采用一种表征作动能量的可控性指标和表征观测信号能量的可观性指标，以确定作动器和传感器的最优位置。试验验证了模型预测控制策略对柔性并联机构振动响应控制的有效性和鲁棒性，取得较为满意的控制效果。

参 考 文 献

[1]宋轶民，余跃庆，张 策，等. 柔性机器人动力学分析与振动控制研究综述 [J]. 机械设计，2003，20(4)：1-5.

SONG Yi-min, YU Yao-qing, ZHANG Ce, et al. Summary on the study of dynamics analysis and vibration control of flexible robots [J]. Machine Design, 2003, 20(4)：1-5.

[2]Sun D, Mills J K, Shan J, et al. A PZT actuator control of a single-link flexible manipulator based on linear velocity feedback and actuator placement [J]. Applied Acoustics, 2004, 14(4)：381-401.

[3]胡俊峰，张宪民. 一种新型两自由度柔性并联机械手的主动振动控制 [J]. 中国机械工程, 2010, 21(17):2017-2024.

HU Jun-feng, ZHANG Xian-min. Active vibration control and its simulation of a novel 2-DoF flexible parallel manipulator [J].China Mechanical Engineering, 2010, 21(17):2017-2024.

[4]胡俊峰，张宪民, 朱大昌，等. 柔性并联机器人动力学建模 [J]. 农业机械学报, 2011, 42(11):208-213.

HU Jun-feng, ZHANG Xian-min, ZHU Da-chang et al. Dynamic modeling of flexible parallel robot [J]. Transactions of the Chinese Society for Agricultural, 2011, 42(11):208-213.

[5]Gasparetto A, Zanotto V. Vibration reduction in a flexible-link mechanism through synthesis of an optimal controller [J]. Meccanica, 2006, 41(6)：611-622.

[6]Iorga L, Baruh H, Ursu I. A Review of H∞robust control of piezoelectric smart structures [J]. Appl. Mech. Rev., 2008, 61(4)：1-16.

[7]张宪民, 袁剑锋. 一种二维平动两自由度平面并联的机器人机构：中国, CN1903521 [P]. 2007-01-31.

[8]Hu J F, Zhang X M, Zhan J Q. Trajectory planning of a novel 2-DoF high-speed planar parallel manipulator [A]. In：1st International Conference on Intelligent Robotics and Applications, ICIRA 2008 [C]. Wuhan, China, 2008：199-207.

[9]胡俊峰，张宪民. 两自由度高速并联机械手的弹性动力学分析 [J]. 华南理工大学学报(自然科学版)，2009, 37(11):123-128.

HU Jun-feng, ZHANG Xian-min. Elastodynamic analysis of a novel 2-DOF high-speed parallel manipulator [J]. Journal of South China University of Technology(Natural Science Edition), 2009, 37(11):123-128.

[10]Guney M, Eskinat E. Optimal actuator and sensor placement in flexible structures using closed-loop criteria [J]. Journal of Sound and Vibration, 2008, 312(1-2)：210-233.