一类非负本原矩阵对

罗美金

(河池学院 数学与统计学院，广西 宜州 546300)

一类非负本原矩阵对

罗美金

(河池学院 数学与统计学院，广西 宜州 546300)

研究一类非负矩阵对，它所对应的伴随有向图中含有两个圈γ1,γ2，公共弧γ1-1→γ1，证明了这类双色有向图本原的充分必要条件，并给出了γ2的顶点数为最小值2时的本原指数上界。

非负；本原；矩阵对；上界

0 引言

n阶非负矩阵对(A,B)与其具有n个顶点的伴随有向图D(A,B)存在一一对应关系。D(A,B)中弧存在与否可由非负矩阵对(A,B)中元素的数值来判断。如：D(A,B)中是否存在红弧(蓝弧)可由矩阵A=(aij)(B=(bij))中元素的数值可判断，若aij>0(bij>0)，则从顶点i到顶点j存在一条红弧(蓝弧)；若aij=0(bij=0)，则从顶点i到顶点j不存在红弧(蓝弧)[1]。

有向图D中只含红弧和蓝弧，那么D是一个双色有向图。如果非负矩阵对(A,B)是本原的，那么非负矩阵对(A,B)所对应的伴随有向图，即双色有向图D(A,B)也是本原的，D(A,B)的本原指数exp(D(A,B))即为非负矩阵对(A,B)的本原指数exp(A,B)。由非负矩阵对的本原指数的概念，可定义双色有向图的本原指数的概念为：

任给定D中的一条途径ω，ω的分解为向量(r(ω),b(ω))或(r(ω),b(ω))T，称ω为一条(r(ω),b(ω))-途径，其中r(ω)和b(ω)分别表示ω中红弧和蓝弧的条数。若存在非负整数h和k，且h+k>0，使得D中的每一对顶点(i,j)都存在从i到j的(h,k)-途径，则双色有向图D是本原的，且h+k的最小值为双色有向图D的本原指数，记作exp(D)。

设D中含有圈γ1,γ2,…,γl,C={γ1,γ2,…，γl}是D的圈集合，定义D的圈矩阵

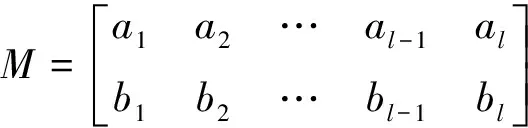
其中ai，bi表示圈γi中的红弧和蓝弧的数目。若M的秩小于2，则M的content(记为content(M))定义为0，否则定义content(M)为M的所有非零2阶主子式的最大公因数。

引理1[2]一个至少包含一条红弧和一条蓝弧的双色有向图D是本原的，当且仅当D是强连通的，且content(M)=1。

目前国内外关于非负本原矩阵对的研究已取得了一些成果[1-6]。本文研究一类非负矩阵对，它所对应的伴随有向图D的未着色图如图1所示。

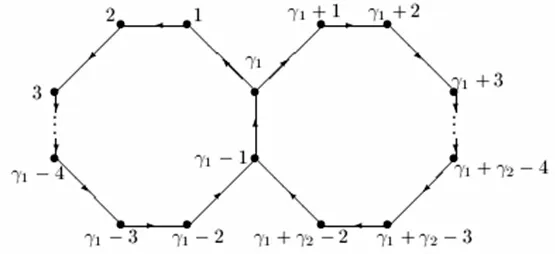
图1 未着色有色图D

由图1可知，D中仅含两个圈，圈长分别为γ1和γ2，两个圈有公共弧γ1-1→γ1。不妨设γ1>γ2≥2，则D的圈矩阵可写为

(1)

其中a,b为正整数，且a≤γ1-1,b≤γ2-1。

1 本原条件

定理1D是如图1的双色有向图，若γ1=km-1,γ2=m，那么D是本原的当且仅当a=k(m-1)-1,b=m-1(k,m∈Z+)。

证明充分性：结合图1，显然，D是强连通的。由引理1，可知D是本原的当且仅当content(M)=1，即det(M)=aγ2-bγ1=am-b(km-1)=±1。由此可得：

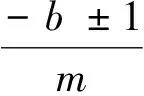
必要性：若a=k(m-1)-1,b=m-1时，易得det(M)=-1，故D是本原的。定理得证。

类似定理1的证明，可得以下三个定理。

定理2D是如图1的双色有向图，若γ1=km+1,γ2=m，那么D是本原的当且仅当a=k(m-1)+1,b=m-1(k,m∈Z+)。

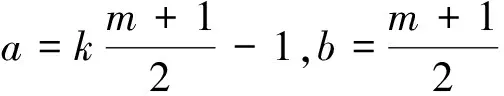
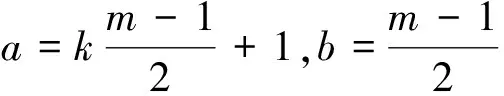
2 γ2=2的指数上界

由定理5可得，det(M)=-1时所对应的圈矩阵及圈矩阵的逆矩阵分别为

det(M)=1时所对应的圈矩阵及圈矩阵的逆矩阵分别为

以下分两种类型讨论双色有向图D的本原指数上界：

类型1：弧γ1-1→γ1是蓝色的；类型2：弧γ1-1→γ1是红色的。

定理6 若如图1的双色有向图D是本原的，det(M)=-1且属于类型1，则

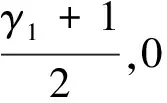
定理7 若如图1的双色有向图D是本原的，det(M)=-1且属于类型2，则

类似定理6、定理7的证明，可得定理8、定理9。

定理8 若如图1的双色有向图D是本原的，det(M)=1且属于类型1，则

定理9 若如图1的双色有向图D是本原的，det(M)=1且属于类型2，则

综合定理6～9，比较各本原指数的大小，可得如图1的双色有向图D的本原指数上界，即定理10。

定理10 若如图1的双色有向图D是本原的，则

[1] B L Shader,S Suwilo.Exponents of nonnegative matrix pairs[J].Linear Algebra Appl,2003,363:275-293.

[2] SHAO Yan-ling,GAO Yu-bin,SUN Liang.Exponent of a class of two-colored digraphs[J].Linear and Multilinear Algebra,2005,53(3):175-188.

[3] GAO Yu-bin,SHAO Yan-ling.Exponent of two-colored double directed cycles[J].Journal of Natural Science of Heilongjiang University,2004(4):55-58.

[4] 罗美金,高玉斌.一类双色有向图的本原指数[J].中北大学学报:自然科学版,2008,29(2):95-100.

[5] 罗美金,高玉斌.一类恰含三个圈的三色有向图的本原指数[J].山东大学学报:理学版,2008,43(1):65-72.

[6] 罗美金.一类双色有向图的本原指数集[J].数学的实践与认识,2012,42(24):253-258.

2014-06-24

广西壮族自治区教育厅项目：双色及多色有向图本原指数的研究(YB2014335)

罗美金(1981-)，女，江西广丰人，河池学院讲师，硕士。研究方向：组合数学。

O157.5

A

1008-4657(2014)04-0072-04

寸晓非]