磁力随钻测量磁干扰校正方法研究
许昊东, 黄根炉, 张 然, 韦红术, 程锋瑞
(1.中国石油大学(华东)石油工程学院,山东青岛 266580;2.中国石油阿姆河天然气公司钻井部,北京 102206;3.中海石油(中国)有限公司深圳分公司,广东深圳 518000)
定向井井眼轨迹控制过程中,需要把MWD安放在无磁钻铤当中,测量井斜角、方位角、工具面角等参数。参数测量精度受到探管所处磁场环境影响,磁干扰使MWD磁通门读数存在误差,导致方位角读数存在误差,降低了井眼轨迹测量精度。现有磁干扰校正方法以单测点磁干扰校正法为主[1-5],近几年又发展出可以在多个测点同时校正磁干扰的多测点校正方法[6-8],基本原理都是参照当地实测磁场强度处理磁通门读数,使处理后的磁通门读数接近当地实测磁场强度。笔者基于单测点磁干扰校正方法,针对常见的径向磁干扰和轴向磁干扰,研究磁干扰校正方法并对其应用效果进行评价,以提高方位角测量精度。
1 MWD测量原理
MWD测量仪器由信号发射器和探管组成,探管内装有两两互相垂直的三轴重力加速度计和三轴磁通门传感器。为叙述方便,不考虑磁偏角和子午线收敛角。以井口为原点O,建立大地坐标系NEV和原点移动至井口的仪器坐标系xyz(见图1)。其中Oz沿探管轴线方向指向探管下部,xy轴在仪器横截面上,x轴与钻头造斜方向一致,仪器坐标轴符合右手法则,重力加速度计和磁通门分布在xyz坐标系3个轴上,测得重力分量和磁场分量分别为gx、gy、gz和Bx、By、Bz。
大地坐标系经过3次旋转可得到仪器坐标系
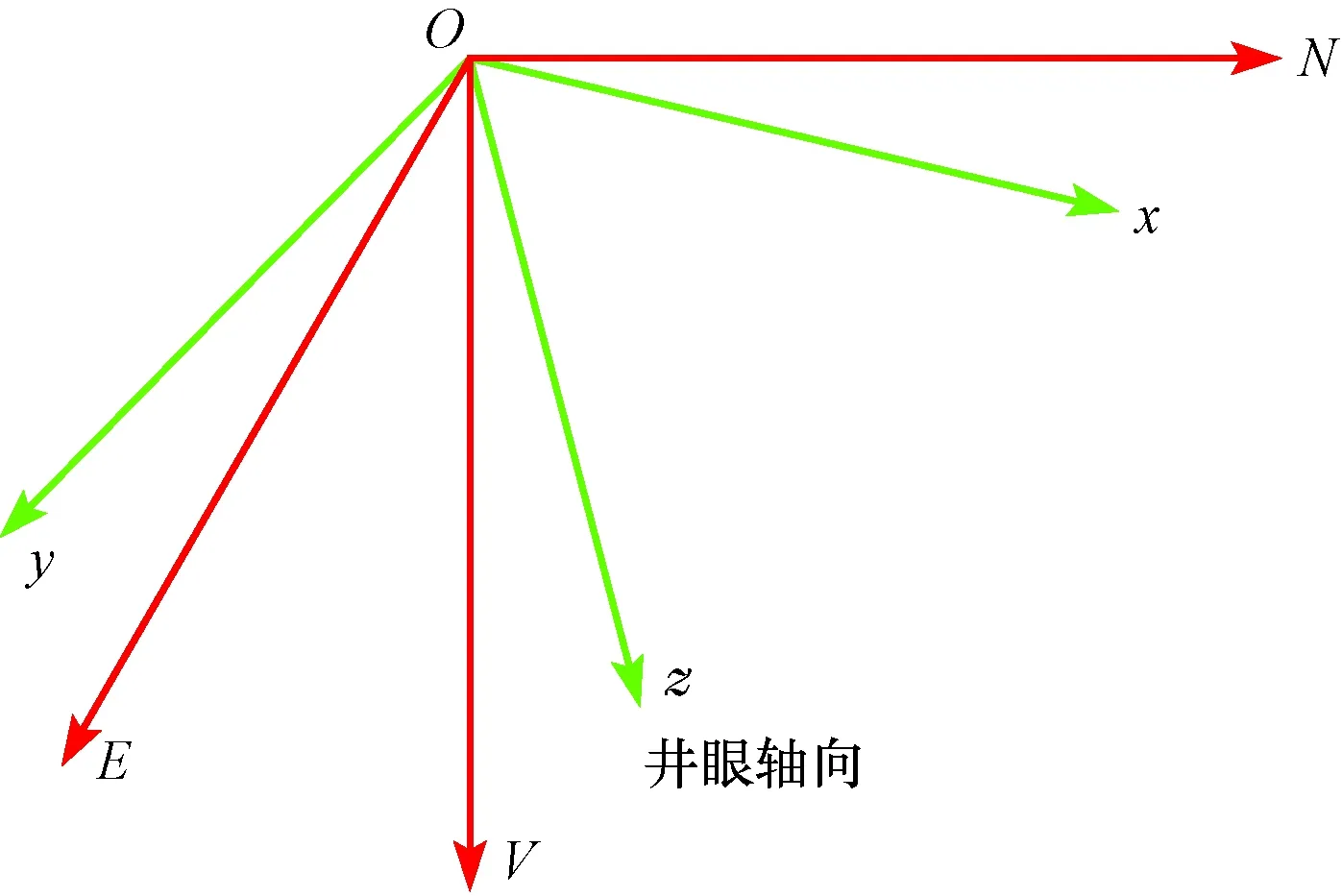
图1 大地坐标系与仪器坐标系Fig.1 Geodetic coordinate system and instrument coordinate system
(见图2),用坐标转换矩阵T表示转换过程[1]。第一次旋转以OV为旋转轴,将N、E分别移动到N1、E1,旋转角度为ψ;第二次旋转以OE1为旋转轴,将V、N1分别移动到z、N2,旋转角度为θ;第三次旋转以Oz为旋转轴,将N2、E1分别移动到x、y,旋转角度为φ,其中θ为井斜角,ψ为方位角,φ为高边工具面角。
大地坐标系等于转换矩阵与仪器坐标系的乘积。大地坐标系下真实的重力场是已知的,通过三轴加速度计读数确定出井斜角和高边工具面角,结合三轴磁通门读数可确定出方位角:
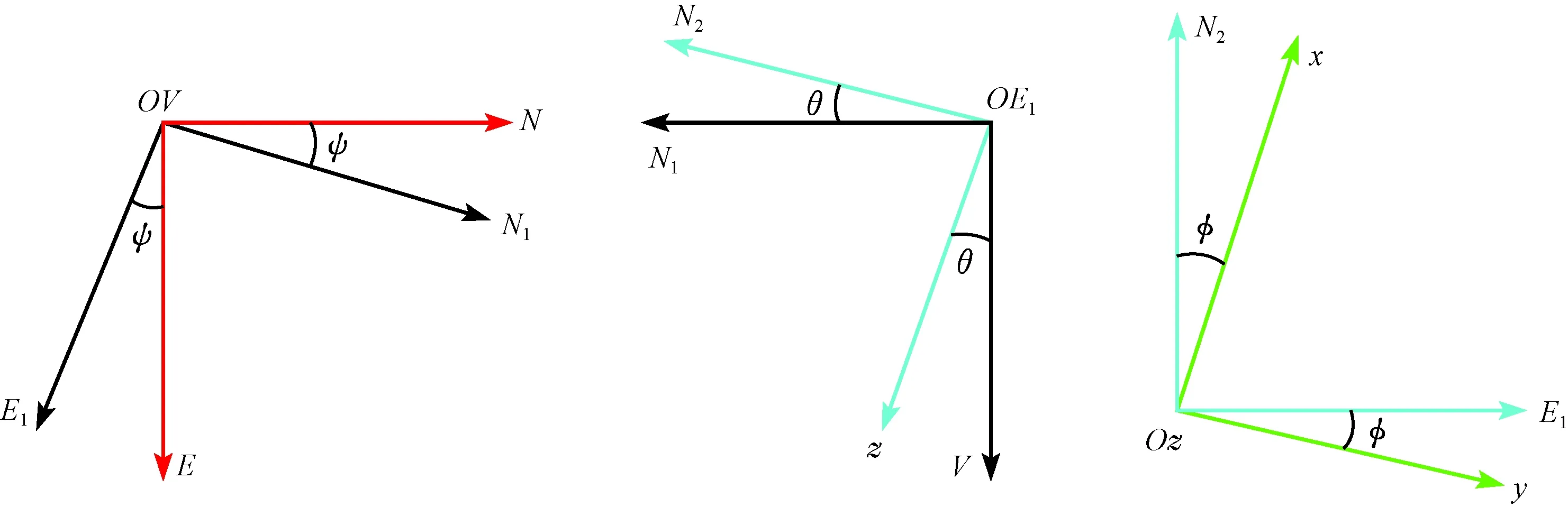
图2 坐标系转换过程Fig.2 Coordinate conversion process
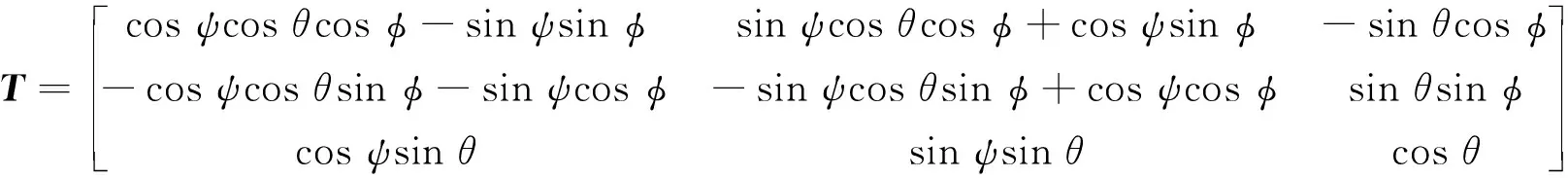
(1)
(2)
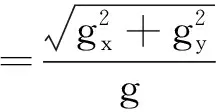
(3)
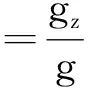
(4)
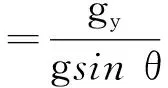
(5)
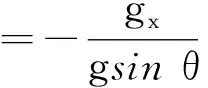
(6)
(7)
2 校正磁干扰
无磁钻铤周围的钻柱组合由铁磁性材料构成,在地磁场作用下发生磁化,主要产生沿仪器轴向的磁干扰。Russell[9]等人研究发现,当无磁钻铤长度大于3.05 m时,磁化产生的径向磁干扰可以忽略不计,也就是说,不考虑钻柱磁化造成的径向磁干扰。目前,制作无磁钻铤的材料主要有以蒙乃尔合金、铬镍合金、铬锰为基础的奥氏体合金、敏铜合金和SMF无磁钢等[10]。由于无磁钻铤材料的化学成分分布不均和加工精度不一致,导致产生局部感应磁和剩磁,这种局部感应磁和剩磁称为磁热点,同时,由于无磁钻铤在使用过程中不可避免的遇到局部冷作,在大钳作用下无磁钻铤也会产生磁热点[11-12]。无磁钻铤上的磁热点将产生径向磁干扰。由于轴向磁干扰和径向磁干扰的来源不同,认为它们是完全耦合的。
在轴向磁干扰和径向磁干扰作用下,三轴磁通门读数存在偏差,导致换算出的方位角存在较大偏差。研究磁干扰时没有考虑邻井套管[13]和测量仪器电池产生的干扰磁场。
2.1 校正径向磁干扰
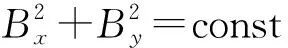
(9)
2.2 校正轴向磁干扰
由于无磁钻铤周围铁磁性钻柱磁化,Oz方向磁通门读数受到干扰,若按照式(6)计算方位角,将会产生较大的误差。在校正轴向磁干扰时,认为径向磁干扰已经被校正。Russell等人[1]提出了一种较为准确的校正方法,徐涛、罗武胜等人[14-15]对该法进行过介绍,但他们选取的坐标系、定义的井斜角和方位角均不符合钻井习惯,而且没有深入研究该方法的有关性质,因此重新简明扼要地介绍Russell法的原理。
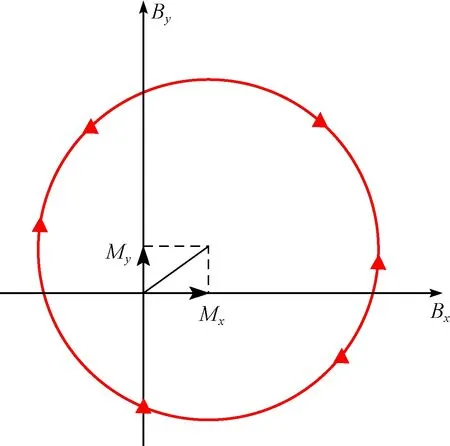
图3 管柱旋转过程中径向磁通门读数Fig.3 Radial magnetometer indication during rotation of pipe
真实地磁场、 轴向干扰磁场和实测磁场分别用B、e和Bm表示,真实方位角ψ和实测方位角ψm之间的偏差角用ψe表示,存在图4所示的空间关系。若不存在轴向磁干扰时,利用式(8)计算的方位角为真实方位角;当存在轴向磁干扰e时,计算出的实测方位角为:
(10)
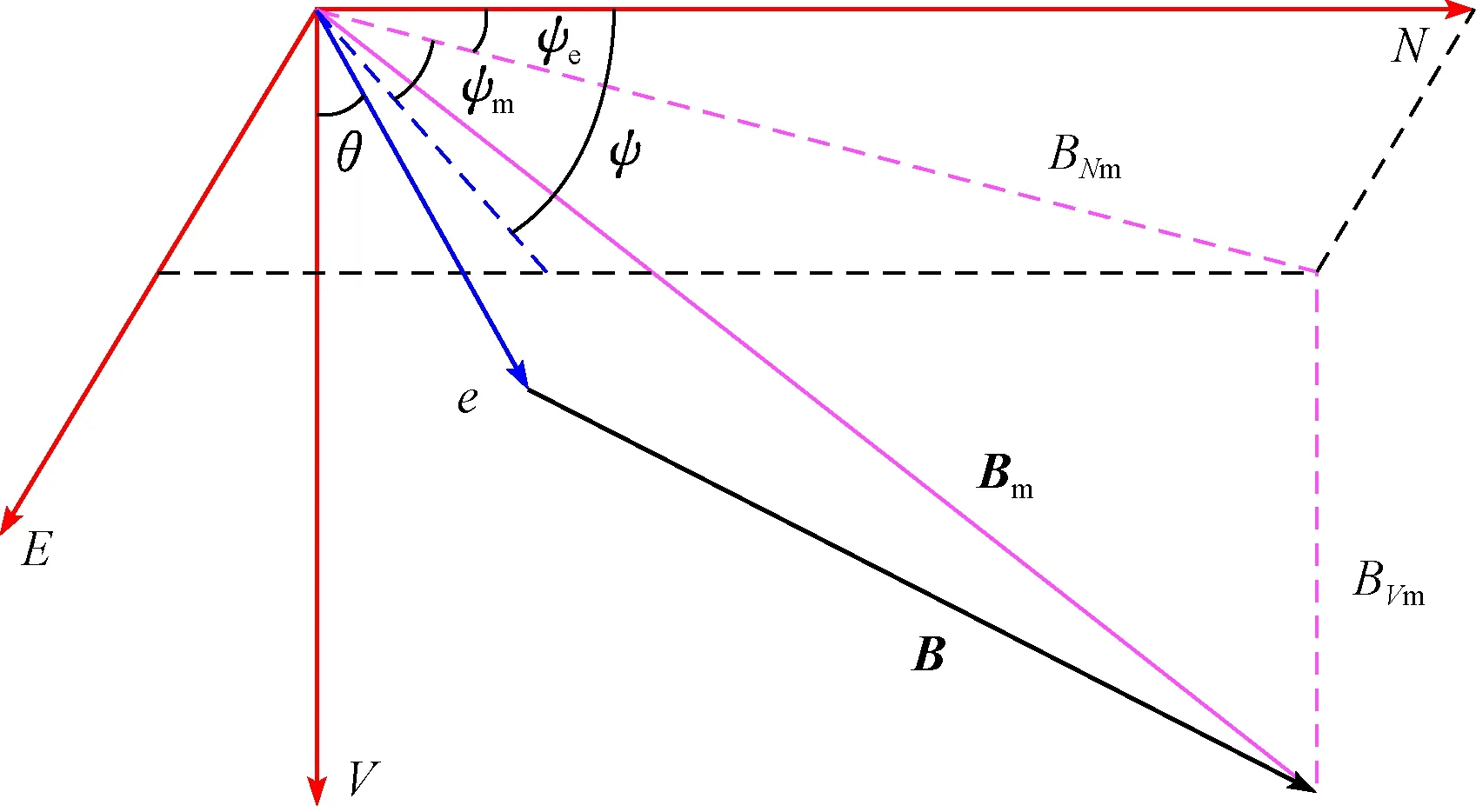
图4 轴向磁干扰的影响Fig.4 Influence of axial magnetic interference
由θ、φ和ψm共同确定出新的转换矩阵T,再由式(7)的变换关系可得Bm的分量:
BNm=cosψm[cosθ(BxCcosφ-ByCsinφ)+Bzsinθ]-sinψm(BxCsinφ+ByCcosφ)
(11)
BVm=-sinθ(BxCcosφ-ByCsinφ)+Bzcosθ
(12)
BEm=0
(13)
设UN、UE、UV分别为北、东、垂向上的单位矢量,真实的地磁场B可分解为水平指北分量BN和垂向分量BV,实测磁场Bm也可以分解在O-NEV坐标系中:
B=BNUN+BVUV
(14)
Bm=BNmUNcosψe+BNmUEsinψe+BVmUV
(15)
上述两式相减得:
em=Bm-B=(BNmcosψe-BN)UN+
BNmUEsinψe+(BVm-BV)UV
(16)
轴向干扰磁场em在仪器坐标系中的取值为[0 0e]T,根据式(7)得:
em=eUNsinθcosφ+eUEsinθsinφ+eUVcosθ
(17)
由式(16)、式(17)可得到ψe的表达式:
(18)
式(18)中存在未知数ψ,采用循环迭代的方法求得ψe:1)用ψm代替ψ代入式(18)求出ψe,根据ψ=ψm+ψe求出ψ;2)设置精度值ε,若|ψ-ψm|≤ε,则ψ为校正后的方位角,结束循环;若|ψ-ψm|>ε,则ψm=ψ,返回步骤1)循环计算。
3 磁干扰校正仿真
按顺序校正径向磁干扰和轴向磁干扰后,可得到校正后的方位角。构造仿真数据来模拟磁干扰校正过程,并根据已有算法编制计算机程序,验证校正方位角的可靠性。已知ε=0.01°,大地磁场强度B=40.0 μT,磁倾角为12°,此时BN=39.126 μT,BV=8.316 μT。
首先,进行仿真径向磁干扰校正。若井眼真实井斜角为30°,真实方位角为60°,旋转钻柱记录工具面角为30°、120°和320°时的径向磁通门读数,并计算得到校正后的径向磁通门读数BxC、ByC。

表1 径向磁干扰校正Table 1 Correction of radial magnetic interference
然后,研究轴向磁干扰校正方法的有关性质。若井眼真实井斜角为30°,真实方位角为60°,真实工具面角为30°,由表1可知校正径向磁干扰后BxC=-5.0871 μT,ByC=-35.736 μT。假设有3组轴向磁干扰e1=1.0 μT、e2=5.0 μT、e3=10.0 μT,随着轴向干扰磁场强度的变化,做出校正方位角随迭代次数的变化(见图5,其中虚线为真实方位角)。随着轴向磁干扰的增大,实测方位角的误差增大,递推计算次数增多,表明轴向磁干扰校正算法具有较好的稳定性。
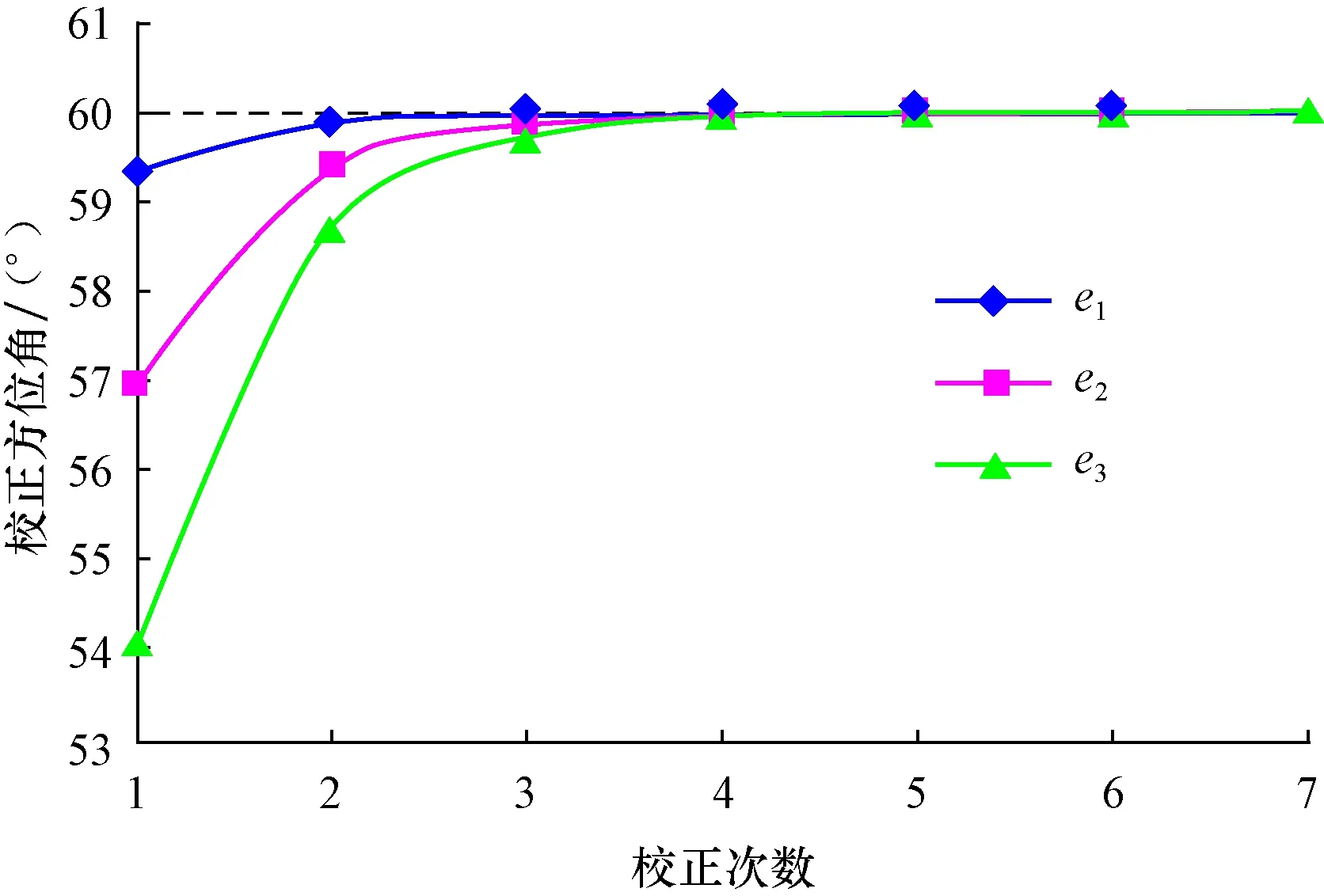
图5 三组轴向磁干扰校正Fig.5 Three groups of axial magnetic interference correction
取e2=5.0 μT,井眼真实方位角为80°,真实工具面角为30°,对井斜角进行一系列变化,测得不同井斜角下的实测方位角和校正方位角变化情况(见图6,其中虚线为真实方位角)。在90°井斜角附近,实测方位角的误差最大,井斜角接近0°或180°(实际不存在)时,实测方位角的误差逐渐减小;在90°井斜角附近,校正方位角与真实方位角仍存在一定微小偏差,在其他井斜角范围内,校正方位角与真实方位角一致。
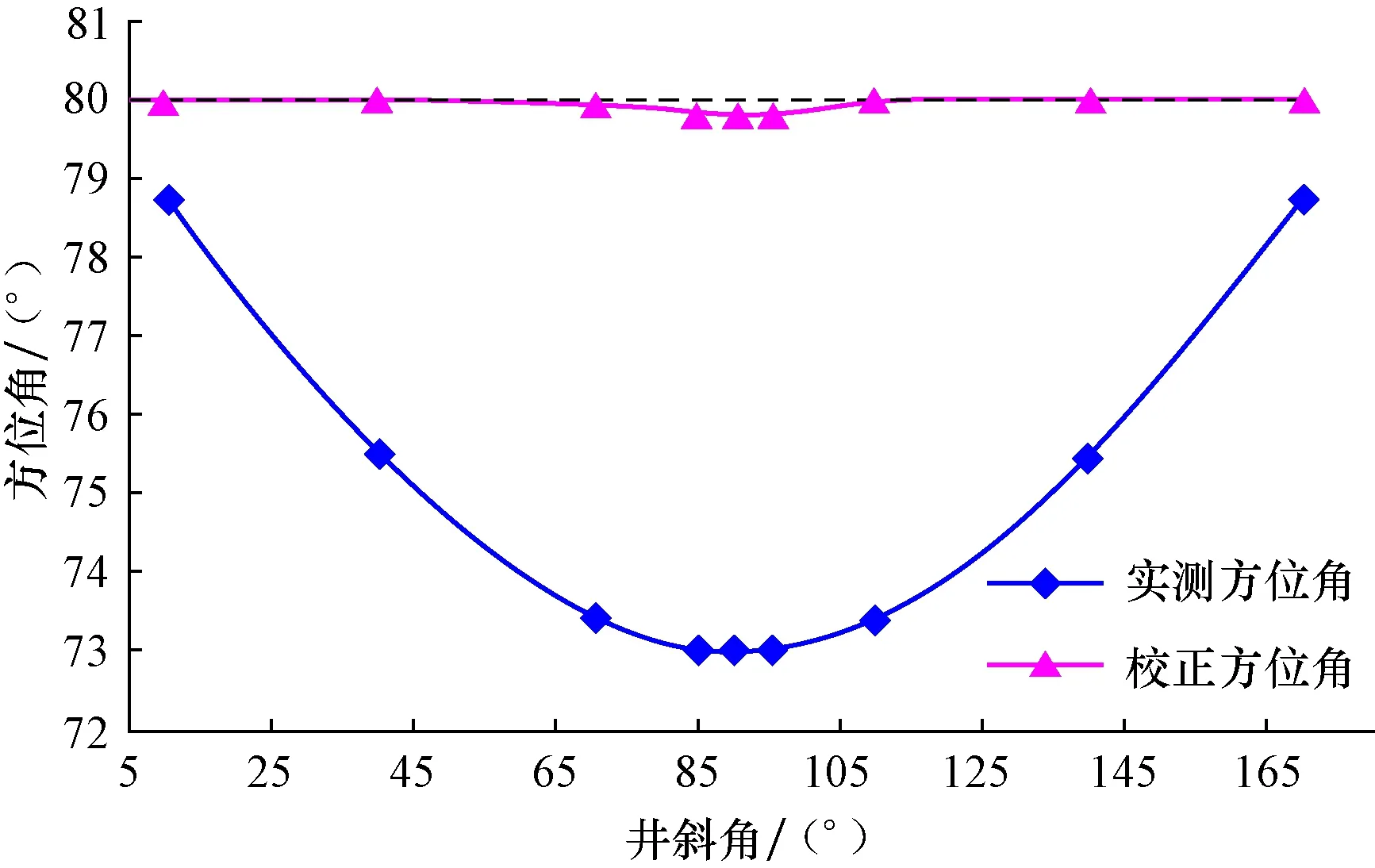
图6 实测方位角、校正方位角与井斜角的关系Fig.6 Relationship between inclination and measured azimuth,corrected azimuth
取e2=5.0 μT,井眼真实井斜角θ=80°,真实工具面角φ=30°,对真实方位角进行实际测量,得到不同真实方位角下的实测方位角和校正方位角(见图7,其中虚线为真实方位角的取值变化),表2为部分源数据。真实方位角为0°~180°时,实测方位角比真实方位角小,真实方位角为180°~360°时,实测方位比真实方位角大,方位角靠近0°或180°时,实测方位误差变小,方位角靠近90°或270°时,实测方位误差变大;当真实方位角接近90°或270°时,校正方位角不能完全达到真实方位角,在其他真实方位角范围内,校正方位角与真实方位角基本一致。
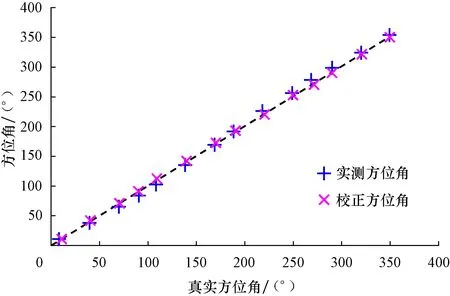
图7 实测方位角、校正方位角与真实方位角的关系Fig.7 Relationship between true azimuth and measured azimuth,corrected azimuth
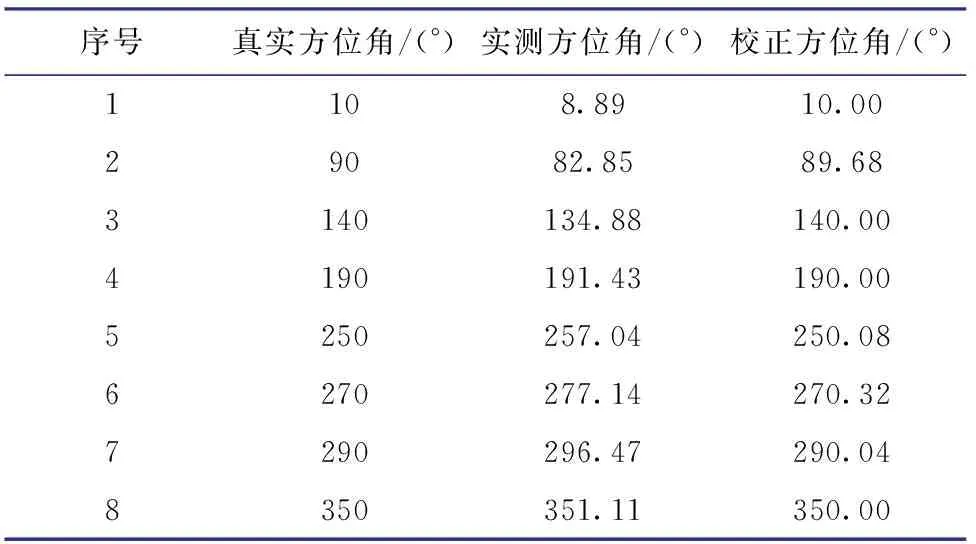
序号真实方位角/(°)实测方位角/(°)校正方位角/(°)1108.8910.0029082.8589.683140134.88140.004190191.43190.005250257.04250.086270277.14270.327290296.47290.048350351.11350.00
4 结 论
1) 进行径向磁干扰校正是保证方位角测量精度的前提。在钻井过程中不需要掌握磁热点在无磁钻铤上的分布情况,只需在井下测量过程中校正磁热点对测量仪器造成的径向磁干扰,通过分析钻柱旋转时记录的离散径向测量数据完成校正。
2) 与井眼轨迹的其他空间分布相比,当井眼轨迹接近水平东或水平西方向时,轴向磁干扰的校正效果最差,这是由于大地磁场在井眼轴向分量过小或等于0,使方位偏差角过小或等于0导致的。
3) 单测点磁干扰校正方法操作简便、算法稳定,能有效提高方位角的测量精度;同时减少无磁钻铤长度,降低钻井成本。建议进一步开展多测点磁干扰校正方法的研究工作。
参考文献
References
[1] Russell M K,Russell A W.Surveying of boreholes:US,4163324[P].1979-08-07.
[2] von Dongen,Johannes C M,Maekiaho Leo B.Method for determining the azimuth of a borehole:US,4682421[P].1987-07-28.
[3] Russell A W.Method of determining the orientation of a surveying instrument in a borehole:US,4819336[P].1989-04-11.
[4] Williamson H S.Accuracy prediction for directional measurement while drilling[J].Journal of Petroleum Technology,1981,33(12):2338-2350.
[5] 王锐,崔朋波,刘培军.MWD独立误差源确定分析[J].特种油气藏,2011,18(5):120-123.
Wang Rui,Cui Pengbo,Liu Peijun.Determinative analysis of MWD independent error sources[J].Special Oil & Gas Reservoirs,2011,18(5):120-123.
[6] Brooks A G.Method of correcting axial and transverse error components in magnetometer readings during wellbore survey operation:US,5623407[P].1997-04-22.
[7] Brooks A G.Method for magnetic survey calibration and estimation of uncertainty:US,6179067B1[P].2001-01-30.
[8] Brooks A G.Multi-station analysis of magnetic surveys:US,8280638B2[P].2010-08-19.
[9] Russell A W,Roesler R F.Reduction of nonmagnetic drill collar length through magnetic azimuth correction technique[R].SPE 13476,1985.
[10] 乔传尚.YST-48R型MWD仪器的Bt值异常分析与判断[J].石油仪器,2011,25(4):23-25.
Qiao Chuanshang.Measurement and analysis of abnormal Bt value of YST-48R MWD[J].Petroleum Instrument,2011,25(4):23-25.
[11] 欧阳奘儒.无磁钻铤磁性对罗盘测量误差的影响[J].石油钻采工艺,1991,13(1):25-31.
Ouyang Zangru.Magnetic properties of nonmagnetic drill collars and their relation to survey compass error[J].Oil Drilling & Production Technology,1991,13(1):25-31.
[12] Edwards J,Pernet F,Jakeman S V J.Magnetic properties of nonmagnetic drill collars and their relation to survey compass error[J].Geoexploration,1979,17(3):229-241.
[13] 张苏,管志川,王建云,等.邻井套管对井斜方位角的影响[J].石油钻探技术,2013,41(6):51-55.
Zhang Su,Guan Zhichuan,Wang Jianyun,et al.Impact of casing on adjacent well azimuth[J].Petroleum Drilling Techniques,2013,41(6):51-55.
[14] 徐涛,温东,孙晓磊.基于加速度计和磁强计的方位测量与校正技术研究[J].仪器仪表学报,2009,30(10):2018-2022.
Xu Tao,Wen Dong,Sun Xiaolei.Research on azimuth measurement and correction technique with accelerometer and magnetometer[J].Chinese Journal of Scientific Instrument,2009,30 (10):2018-2022.
[15] 罗武胜,徐涛,杜列波.基于加速度计和磁强计的定向钻进姿态测量及方位角校正[J].国防科技大学学报,2007,29(1):106-110.
Luo Wusheng,Xu Tao,Du Liebo.Directional drilling attitude measurement and azimuth correction with accelerometers and magnetometers[J].Journal of National University of Defense Technology,2007,29(1):106-110.

