Macondo深水井漏油事故防喷器系统失效原因分析
金业权, 胡 满, 吴 谦, 纪永强
(中国石油大学(华东)石油工程学院,山东青岛 266580)
1 概 述
2010年发生在美国墨西哥湾的Macondo深水井漏油事故中,由于防喷器系统失效,井喷未能得到有效控制,造成了十分严重的后果。目前,深水防喷器系统的故障数据主要来源于美国安全与环境执法局网站上e-Well系统收录的2007—2009年美国墨西哥湾外大陆架所钻259口深水井的油气井活动报告[1]。根据统计,深水防喷器系统常见的失效模式有黄蓝箱自身功能故障、蓄能器液压供应不足、万能防喷器内部泄漏、液压连接器解锁故障、闸板防喷器内部泄漏或无法关闭、柔性接头外部泄漏和节流压井阀外部泄漏等,其中约有50%的故障是由控制系统失效引起的,危害性较为严重的有液压连接器解锁故障、闸板防喷器关闭故障、万能防喷器关闭故障等。
在探讨深水防喷器系统失效主要原因时,国内学者多是针对单一部件或某一子系统,主要是对控制系统进行可靠性研究[2]。由于防喷器系统是一个复杂的系统,单个部件或某一子系统是否可靠的结论,对实际生产不具指导价值。一些学者对深水防喷器系统整体的可靠性进行了初步探索[3-4]。但是,基于故障树分析法,以深水防喷器系统为研究对象,对Macondo深水井漏油事故进行定性和定量相结合的系统失效原因分析,在国内鲜有报道。
为此,笔者根据Macondo深水井漏油事故中防喷器失效的相关资料,建立了Macondo井的深水防喷器系统失效故障树;对该故障树进行定性与定量计算分析,找出了导致系统失效的关键因素和诱因组合;应用该故障树模型,对Macondo井喷漏油事故进行了系统失效原因分析;并对系统失效概率的近似计算与实际情况进行对比,验证识别了主要失效原因的客观性。
2 防喷器系统失效故障树的构建
故障树分析法是一种评价复杂系统可靠性与安全性的重要方法。故障树分析法的一般步骤包括:确定顶事件、调查原因事件、编制故障树和分析故障树。故障树的完善程度和准确程度直接决定故障树分析结果的可靠性和有效性,因此故障树的构建是整个故障树分析法的关键。为了建立较为可信的Macondo井深水防喷器系统失效故障树,笔者结合国外一些团体和企业对该事故的调查报告[5-8],对顶事件的发生原因和经过进行了详细分析,找到了导致系统失效的因素集,并在此基础上构建了故障树。
2.1 顶事件的确定
顶事件是不希望发生的失效事件。在防喷器系统的失效分析中,确定顶事件(T)为“防喷器组没有封住井口”。
2.2 Macondo井防喷器系统失效过程分析
在Macondo深水井漏油事故中,直到油气进入隔水管时作业人员才发现井涌,然后立即关闭上部万能防喷器。由于发现溢流不及时,油气上返速度太快,钻杆受到很大提升力,使得钻杆接头的一部分到了上部万能防喷器的橡胶密封元件之上。在万能防喷器完全关闭所需要的26 s内,通过橡胶密封元件和钻杆接头之间空隙的油气岩屑流的流速迅速增大,对密封元件和钻杆接头造成严重侵蚀,万能防喷器密封失效。同时,上部万能防喷器上方的钻杆也受到了严重侵蚀。
之后,平台作业人员又关闭了上部、中部2个变径闸板防喷器(VBR),并用机械闸板防喷器锁定装置(ST锁)锁紧,VBR关井成功。爆炸导致钻机断电后,平台的定位系统失效,随着平台位置的偏离,钻机游车与防喷器组之间的钻杆受到拉力,短短几分钟内,上部万能防喷器上方之前受到严重侵蚀的钻杆在拉力作用下发生了断裂,先前被封闭在VBR下方的流体通过钻杆断口再次喷出井口。
于是,平台工作人员试图关闭全封剪切闸板防喷器(BSR)。爆炸损坏了多路电液控制系统(MUX)电缆,使受控于地面控制面板的紧急解脱系统(EDS)失效。平台工作人员试图通过黄蓝控制箱激活自动模式(AMF)功能,但未激活。在BP公司墨西哥湾漏油事故的事后调查中发现,黄箱103电磁阀损坏,蓝箱供给SEM B的蓄电池和控制箱的蓄电池电量不足,无法激活103电磁阀,AMF没有被激活。之后,平台工作人员试图通过水下机器人(ROV)控制液压接头干预关闭剪切闸板,但由于水下机器人的泵失效、输出流量低以及水下蓄能器泄漏,导致控制液压接头无压力,这个尝试也失败了。最后,通过水下机器人驱动并剪断自动剪切杆,自动剪切功能被激活,BSR开始关闭。但是,由于一个工具接头穿过剪切闸板,BSR无法剪断且无法完全关闭。到此,防喷器组完全失效了。
2.3 Macondo井防喷器系统失效故障树的编制
基于以上Macondo井防喷器系统失效分析,建立了具有21个中间事件(E1—E21)和14个基本事件(X1—X14)的防喷器组失效故障树(见图1)。
3 防喷器组失效故障树定性分析
故障树分析包括定性分析和定量分析,求解故障树的最小割集、最小径集和各基本事件结构的重要度属于定性分析的范畴,在已知各基本事件发生概率的条件下求解顶事件的发生概率属于定量分析。
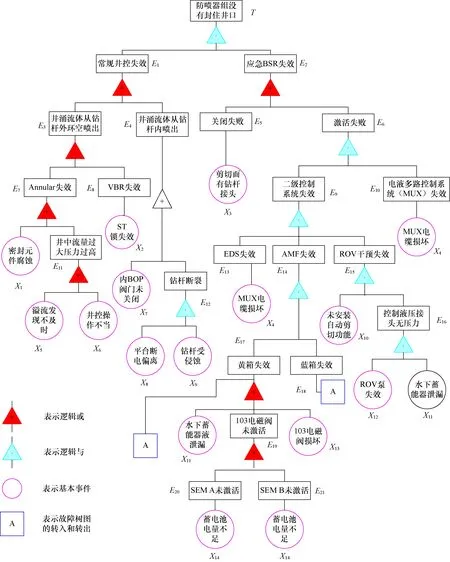
图1 “防喷器组没有封住井口”的故障树Fig.1 Fault tree of BOP failed to seal the well
3.1 故障树最小割集的求解
最小割集是指引起顶事件发生的最低限度的基本事件集合。任何一个最小割集中的基本事件同时发生,顶事件都会发生。通过求解故障树的最小割集,可以得到系统故障发生的所有模式。最小割集数量越多,表示系统的故障模式越多,系统也就越危险[9-10]。通常用布尔代数化简法求解故障树最小割集,求解过程为:
T=E1E2=(E3+E4)(E5+E6)=(E7E8+X7+E12)(X3+E9E10)=
[(X1+X5+X6)X2+X7+X8X9](X3+E13E14E15X4)=
(X1X2+X2X5+X2X6+X7+X8X9)[X3+X4E17E18X10E16X4]=
(X1X2+X2X5+X2X6+X7+X8X9)[X3+(X11+X14+X13)X10X11X12X4]=
(X1X2+X2X5+X2X6+X7+X8X9)(X3+X4X10X11X12)=X1X2X3+X1X2X4X10X11X12+
X2X5X3+X2X5X4X10X11X12+X2X6X3+X2X6X4X10X11X12+
X7X3+X7X4X10X11X12+X8X9X3+X8X9X4X10X11X12
(1)
从式(1)可以看出,进行布尔代数化简后得到X1X2X3等10个最小割集,具体见表1。
表1Macondo井深水防喷器系统失效故障树最小割集
Table1MinimalcutsetsinafaulttreefordeepwaterBOPsysteminMacondowell

割集阶数(数量)最小割集二阶割集(1)(X3X7)三阶割集(4)(X1X2X3),(X2X3X5),(X2X3X6),(X3X8X9)五阶割集(1)(X4X7X10X11X12)六阶割集(4)(X1X2X4X10X11X12),(X2X4X5X10X11X12),(X2X4X6X10X11X12),(X4X8X9X10X11X12)
表1中,10个最小割集表示系统失效的10种情况。其中,最低阶数割集为X3X7,说明最容易导致防喷器系统失效的原因组合是剪切面有钻杆接头和内防喷器阀门未关闭。由前述Macondo井防喷器系统失效过程分析可知,Macondo井喷漏油事故中的基本事件X1,X3,X4,X5,X6,X8,X9,X10,X11,X12,X13和X14均发生了。参照表1可知,导致Macondo井喷漏油事故发生的原因组合为(X3X8X9)和(X4X8X9X10X11X12),根据最小割集的定义,其中任何一个原因组合的发生都可导致Macondo井漏油事故的必然发生。
3.2 最小径集的求解
最小径集是指不能引起顶事件发生的最低限度基本事件集合。任何一个最小径集中的各基本事件不同时发生,顶事件就不会发生。最小径集数量越多,说明控制系统不发生故障的方法就越多,系统也就越安全。
通常利用最小径集和最小割集的对偶性来求解最小径集,其具体步骤是:首先构建故障树的对偶树(即成功树),其方法是在故障树图的基础上,将所有的“与”门变成“或”门,所有的“或”门变成“与”门,得到成功树;然后,利用布尔代数化简法求解成功树的最小割集,即原故障树的最小径集。成功树最小割集(故障树最小径集)的求解过程为:
T'=E1+E2=E3E4+E5E6=(E7+E8)X7E12+X3(E9+E10)=
(X1E11+X2)X7(X8+X9)+X3(E13+E14+E15+X4)=
(X1X5X6+X2)X7(X8+X9)+X3(X4+E17+E18+X10+E16+X4)=
(X1X5X6+X2)X7(X8+X9)+X3(X4+X11X13X14+X10+X11+X12)=X1X5X6X7X8+
X1X5X6X7X9+X2X7X8+X3X7X9+X3X4+X3X11X13X14+X3X10+X3X11+X3X12
(2)
从式(2)可以看出,进行布尔代数化简后得到X1X5X6X7X8等9个最小径集,具体见表2。
表2Macondo井深水防喷器系统失效故障树最小径集
Table2MinimalpathsetsinafaulttreefordeepwaterBOPsysteminMacondowell

径集阶数(数量)最小径集二阶径集(4)(X3X4),(X3X10),(X3X11),(X3X12)三阶径集(2)(X2X7X8),(X2X7X9)四阶径集(1)(X3X11X13X14)五阶径集(2)(X1X5X6X7X8),(X1X5X6X7X9)
表2中,9个最小径集表示防止系统失效的9种办法,4个二阶径集表示防止系统失效的4种最简单的方法。
3.3 计算基本事件的结构重要度
结构重要度分析就是不考虑各基本事件的发生概率有多大,仅从故障树结构上分析各基本事件的发生对顶事件发生的影响程度。精确计算各基本事件结构重要度比较繁琐,通常利用最小割集或最小径集来近似求取各基本事件的结构重要度系 数。近似计算判别式为[10]:
(3)
式中:Ii为基本事件Xi结构重要度的近似判别值,Ii越大则结构重要度Iφ i越大;Xi∈Kj表示基本事件Xi属于Kj最小割(径)集;nt为基本事件Xi所在最小割(径)集中基本事件的个数。
由于防喷器系统失效故障树的最小径集比最小割集形式要简单,所以利用最小径集求解结构重要度近似值。利用式(3)计算得到各个基本事件的重要度得到:I1=I5=I6=I13=I14=0.125,I2=I4=I10=I12=0.5,I3=2.125,I7=I11=0.625,I8=I9=0.312 5。将以上近似值从大到小排序,得到结构重要度排序:Iφ3>Iφ7=Iφ11>Iφ2=Iφ4=Iφ10=Iφ12>Iφ8=Iφ9>Iφ1=Iφ5=Iφ6=Iφ13=Iφ14。
以上分析可知,剪切面有钻杆接头、内BOP阀门未关闭和水下蓄能器泄漏等3个基本事件对防喷器系统的失效影响最大,是导致系统失效的关键诱因。这些因素分别属于防喷器设计方面、人员操作方面和系统监测方面的问题。
4 深水防喷器系统失效概率的近似计算方法
4.1 概率近似计算公式
设故障树有n个最小割集Gi(1≤i≤n),则系统的故障事件可表示为:
T=G1+G2+…+Gn
(4)
式中,每个最小割集Gi(1≤i≤n)是基本事件Xj(1≤j≤m,m为基本事件数目)的积事件。一般情况下,最小割集彼此相交,根据相容事件的概率计算公式,设顶事件发生概率为P(T),则:
P(T)=P(G1+G2+…+G3)=
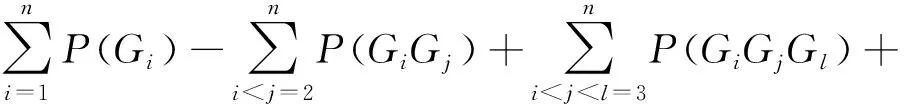
(-1)n-1P(G1G2…Gn)
(5)
从式(5)可以看出,当最小割集数目较大时,式中项数很多,按照传统的近似计算方法,即选取该式的第一项或前面部分项进行近似计算误差较大,特别是在故障树的基本事件发生概率较大的时候[11]。因此,在近似计算时选取精确解公式(即式(5))的前2项,并为了减小相对误差对第2项乘以最优权因子,由此得到顶事件发生概率近似计算公式为:
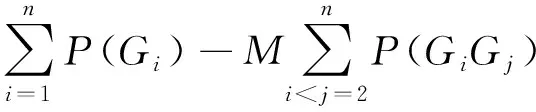
(6)
式中:M为最优权因子,根据基本事件概率分布区间从最优权因子表(见表3)[12]中取值。
4.2 顶事件最小割集的简化
最小割集中所含基本事件数目越多,该最小割集发生的概率越小。因此,在各基本事件发生概率不太高的情况下,舍弃高阶割集对顶事件概率计算造成的理论误差不大。为了进一步简化顶事件概率计算,采用了截尾技术,即规定最小割集中基本事件的数目不超过4个,对于超过4个基本事件的割集在概率计算中不参与运算。因此,式(1)可以简化为:

T≈X3X7+X1X2X3+X2X3X5+X2X3X6+X3X8X9 (7)
4.3 顶事件概率计算过程
将式(7)代入式(6)进行近似计算。计算过程中要注意,在求组合概率积时必须消去重复的概率因子,例如P(X3X7X1X2X3)=P(X3X7X1X2),具体计算步骤为:
P(T)≈P(X3X7+X1X2X3+X2X3X5+X2X3X6+X3X8X9)=
P(X3X7)+P(X1X2X3)+P(X2X3X5)+P(X2X3X6)+P(X3X8X9)-
M[P(X3X7X1X2)+P(X7X2X3X5)+P(X2X3X6X7)+P(X7X3X8X9)+P(X1X2X3X5)+
P(X1X2X3X6)+P(X1X2X3X8X9)+P(X2X3X5X6)+P(X2X3X5X8X9)+P(X2X3X6X8X9)]=
p3p7+p1p2p3+p2p3p5+p2p3p6+p3p8p9-M(p3p7p1p2+p7p2p3p5+p2p3p6p7+
p7p3p8p9+p1p2p3p5+p1p2p3p6+p1p2p3p8p9+p2p3p5p6+p2p3p5p8p9+p2p3p6p8p9)
(8)
式中:pi(1≤i≤n)为第i个基本事件发生的概率。
由于各基本事件发生的一般概率数据很难获得,所以采用专家调查法对基本事件X1,X2,X3,X5,X6,X7,X8,X9按照表4[13]中的5个等级进行概率高低评判。综合各专家意见得出的结果为:X3,X5,X7的发生概率为非常高等级;X1,X6,X9为高等级;X2,X8为中等级。
根据表4中概率值和语言变量的转换关系可得:pi≥1.0×10-1(i=3,5,7);1.0×10-2≤pj<1.0×10-1(j=1,6,9);1.0×10-3≤pk<1.0×10-2(k=2,8)。各取最小值,得pi(i=3,5,7)=0.1;pj(j=1,6,9)=0.01;pk(k=2,8)=0.001。由此,参照表3可得M=1,代入式(8)得P(T)min=0.010 01,处于高概率等级。这表明,Macondo深水井漏油事故中,深水防喷器系统失效的概率高,存在的井喷漏油风险高。而由“2.2 Macondo井防喷器系统失效过程分析”可知,基本事件X1,X3,X5,X6,X8和X9均发生了,与专家评判结果基本一致;并且,由于上述基本事件的发生,最后导致Macondo深水井防喷器系统彻底失效而发生井喷,说明该井防喷器系统的失效概率确实高。顶事件计算结果与实际情况基本相符,验证了失效原因分析的正确性。

表4 概率值和对应的语言变量Table 4 Probability values and the corresponding linguistic variables
注:L为每天发生基本事件的次数。
5 结 论
1) 基于故障树分析法,结合Macondo井防喷器失效过程分析,建立了Macondo井深水防喷器系统失效故障树。
2) 求解了Macondo井深水防喷器系统失效故障树的最小割集与最小径集,对基本事件的结构重要度进行了排序,找出了系统失效的10种模式,为深水防喷器系统失效分析提供了一种可供借鉴的方法。
3) 对基本事件进行了结构重要度计算,识别出了防喷器失效的主要原因。
4) 顶事件概率计算发现,Macondo井防喷器系统失效的概率较高,这与实际情况是相符的,验证了Macondo井防喷器失效原因分析的正确性;而且,该研究结果有助于对Macondo深水井漏油事故进行更深入的分析。
参考文献
References
[1] Holand P.Reliability of subsea BOP systems for deepwater application[R].STF38 F97417,1997.
[2] 李博.深水海底防喷器组液压控制系统设计研究[D].青岛:中国石油大学(华东)机电工程学院,2009.
Li Bo.Deepwater subsea BOP stacks hydraulic control system design and research[D].Qingdao:China University of Petroleum(Huadong),School of Mechanical and Electrical Enginee-ring,2009.
[3] 段明星,李明亮,陈瑞峰,等.深水防喷器系统可靠性探讨[J].中国造船,2010,51(增刊2):297-302.
Duan Mingxing,Li Mingliang,Chen Ruifeng,et al.Discussion on the reliability of deepwater subsea blowout preventer system[J].Shipbuilding of China,2010,51(supplement 2):297-302.
[4] 刘翔.3000m深水下防喷器组可靠性研究[D].青岛:中国石油大学(华东)机电工程学院,2010.
Liu Xiang.Research on reliability of subsea BOP stacks for the depth of 3000 meters[D].Qingdao:China University of Petroleum(Huadong),School of Mechanical and Electrical Engineering,2010.
[5] BP plc.Deepwater horizon accident investigation report[R].2010.
[6] Holand P,Awan H.Reliability of deepwater subsea BOP systems and well kicks[R].Houston:ExproSoft Inc,2012.
[7] Deepwater Horizon Study Group.Final report on the investigation of the Macondo Well blowout[R].2011.
[8] Transocean Inc.Macondo Well incident transocean investigation report[R].2011.
[9] 刘刚,金业权.钻井井控风险分析与控制[M].北京:石油工业出版社,2011:83-86.
Liu Gang,Jin Yequan.Drilling well control risk analysis and control[M].Beijing:Petroleum Industry Press,2011:83-86.
[10] 刘绘珍,张力,王以群,等.故障树中最小割集和最小径集的改进算法[J].工业安全与环保,2006,32(4):58-59.
Liu Huizhen,Zhang Li,Wang Yiqun,et al.One advanced calculation method for the least cut set and least path set of fault tree[J].Industrial Safety and Environmental Protection,2006,32(4):58-59.
[11] 孙逊.基于FTA的故障诊断分析算法的研究[D].大连:大连理工大学控制科学与工程学院,2009.
Sun Xun.The study of fault diagnosis algorithm based on FTA[D].Dalian:Dalian University of Technology,School of Control Science and Engineering,2009.
[12] 孙东平,姚奕,马瑞萍.故障树近似计算中最优权因子的选取[J].指挥控制与仿真,2006,28(3):97-98.
Sun Dongping,YaoYi,Ma Ruiping.Choice of the best parameter in fault tree analysis approximate computation[J].Command Control & Simulation,2006,28(3):97-98.
[13] Pillay A,Wang J.A risk ranking approach incorporating fuzzy set theory and grey theory[J].Engineering Reliability & System Safety,2003,79(1):61-67.

