FRP约束混凝土柱应力-应变计算模型及其比较

薛东智

(陕西建工集团总公司,陕西西安710003)

纤维复合材料(FRP)作为一种新型结构加固材料，逐渐被建筑业人士所接受。它具有高强、轻质、耐腐、耐久、便于施工等诸多优点，在建筑领域应用越来越广泛。它可以加固各种结构，如桥梁、隧道、工业与民用建筑和结构构件，如梁、板、柱、剪力墙等。但因为这项技术在建筑业的应用较晚，研究尚不成熟，仍有大量工作需要做，尤其随着FRP约束混凝土的力学性能研究的不断的深入，热点问题还将集中在应力-应变关系的研究。

关于FRP约束混凝土的应力-应变关系目前已有较多的研究成果，其中以对圆形截面柱的研究居多，近年来开始研究方、矩形截面柱。应力-应变关系是工程结构材料的物理关系，是其内部微观机理的宏观行为表现，是结构强度和变形计算中必不可少的依据。为了研究FRP约束混凝土构件的力学性能和承载力设计方法，必须确定混凝土在FRP复合材料约束情况下的应力-应变关系模型。

基于试验观测，不同的研究者对FRP约束混凝土的应力-应变关系描述基本一致[1-3]：FRP约束混凝土在弹性阶段的应力-应变关系曲线和无约束混凝土的曲线基本重合，表明此时FRP基本未对混凝土产生有效约束作用。随着荷载的继续加大，当混凝土的应力接近素混凝土抗压强度时，素混凝土由于没有横向约束作用，在竖向产生一些微细裂缝，并不断扩展，最终导致混凝土被压碎，应力-应变关系进入下降段;而FRP约束混凝土在轴向加载过程中随着混凝土的横向膨胀，将促进FRP的环向应变迅速增长，使混凝土的应力仍能有效增长，其增长的幅度将取决于截面形状、FRP加固量、纤维缠绕方向等因素，此时试件的极限强度和变形能力均有明显的提高。试件进入破坏阶段时由于FRP约束大小的不同，约束后混凝土的应力-应变关系存在强化和软化两种情况。对于方形或矩形等非均匀约束截面，FRP的约束效果要差，大都出现软化现象。试件最终破坏是由于FRP达到极限应变而被拉断，破坏的发生具有突然性。

1 典型的FRP约束混凝土模型

为了模拟上述应力-应变关系，不同的研究者先后提出了不下数十种计算模型，不同的模型的计算结果存在较大的差异。这些模型大致可以分为用于设计和用于分析两大类。用于设计的模型是基于对大量实测应力-应变关系曲线的统计分析，采用不同的方程形式对其进行直接模拟。模型间的主要差别在于如何合理考虑FRP对混凝土的约束作用。由于实验时所用的纤维特性、树脂特性、纤维铺设方向、截面形状及混凝土特性等均不尽相同，加上试验结果本身存在离散性，目前尚没有一种被广泛认可的模型。用于分析的模型是基于混凝土的侧向膨胀规律，计算FRP的应力和混凝土受到的约束力，根据已有的受定侧压力下的混凝土的应力-应变关系来确定FRP约束混凝土的应力-应变关系。由于FRP对混凝土的约束是被动的，上述计算需要通过大量的迭代才能完成。用于分析模型的计算结果是否足够准确主要取决于对混凝土侧向膨胀规律模拟的准确程度。虽然关于钢约束混凝土的性能已有大量的研究，但是近来的研究表明，针对钢约束混凝土的轴压强度模型不能直接用于FRP约束混凝土，其计算结果对于FRP约束混凝土来说是偏于不安全的。通过国内外学者多年来对FRP约束混凝土柱力学性能和设计方法开展了深入细致的研究，已取得了丰硕的成果。现将典型模型总结如下。

1.1 Fardis模型[4]

(5)

1.2 Mander模型[5]

基于Popovics提出的混凝土应力-应变关系，Mander等人提出钢约束混凝土的应力-应变模型，这一模型曾被一些研究者用于FRP约束混凝土。该模型可适用于在水平应力为fr时求解圆形箍筋或方形箍筋约束混凝土构件的情况。

(6)

1.3 Samaan模型[6]

Samaan等提出一种FRP约束混凝土核心混凝土的应力-应变关系模型如下：

(7)

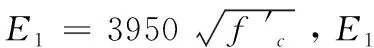
1.4 Toutanji模型[7]

Toutanji模型采用两段式来描述FRP约束混凝土核心混凝土的应力-应变关系模型，过渡区(连接点)很平缓，即：

(8)

(9)

1.5 Spoelstra模型[8]

在 mander模型的基础上，Spoelstra提出了FRP约束混凝土核心混凝土的应力-应变关系模型如下：

(10)

其中:

1.6 K.Miyauchi 模型[9]

因为加强柱最初刚度与普通混凝土的最初刚度相等，而且混凝土进入塑性阶段后应力-应变曲线接近直线，Miyauchi认为纤维片材加强混凝土的轴向应力-应变曲线可以用抛物线及其切线模拟，即：

0≤εc≤εtan时，

(11)

εtan≤εc≤εcc时，

(12)

λ=

1.7 Xiao和Wu模型[10]

σc=Ecεc+2vcfr

(13)

(14)

2 FRP约束混凝土模型分析评价

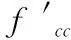
所有的FRP约束混凝土的应力-应变模型都可以计算出极限轴向应变。笔者在对这些研究成果的整理过程中发现：上述各类方法都有各自的特点，但是在进行FRP约束混凝土应力-应变关系计算时，计算结果存在较大的差异。为了具体地了解上述各类计算方法的特点和分析其差异,下面用上述几种模型来计算分析两组实验结果。限于篇幅，在此仅对分析结果绘制应力-应变曲线图,图1中散点为试验数据，实线为各模型的计算结果。其中，两组试验中采用的CFRP的抗拉强度和弹性模量分别为1 577 MPa和105 000 MPa，粘贴层数分别为图1(a)为1层，图1(b)为2层，而试件均为直径150 mm、高300 mm的混凝土圆柱体，混凝土强度等级为34.2 MPa。

(a)

(b)图1 应力-应变曲线模型分析

由应力-应变曲线图中结果比较可见,在约束混凝土试件受力变形的初期阶段，各个模型计算出的理论值与试验值相差不大，因此，此阶段的受力变形不是研究的重点；在约束受力变形阶段，各个计算模型所得的理论曲线与试验曲线的误差有了明显的差别：由Xiao模型计算出的理论曲线与各实验曲线产生的误差最小，其次是Toutanji模型和K.Miyauch模型。

各类模型的计算结果之间存在较大差异,且没有任何一种模型可以较好模拟试验结果，大部分模型高估了CFRP约束混凝土的极限轴向应变。分析其原因，笔者认为：(1)这些模型的一个共同的缺点是未考虑FRP种类的影响；(2)由于实验时所用的纤维特性、树脂特性、纤维铺设方向、截面形状及混凝土特性等均不尽相同，加上试验结果本身存在离散性，而每一种模型均是在各自的试验基础上提出的，混凝土的材料离散，试验方法、试验仪器与测量手段又不统一，因此模型在对试验数据分析中误差较大；(3)模型中所考虑的影响FRP约束混凝土力学性能的因素是否全面是决定该模型与试验数据吻合好坏的关键；(4)模型建立的试验基础广泛与否对模型模拟是否准确起着重要的作用。后几种模型提出的时间相对较晚，模型建立时研究的试验结果种类较多，因此，对FRP约束混凝土应力-应变曲线模拟较好，前几个相对较差。

3 结论

随着FRP材料应用的日趋广泛，国内外对FRP约束混凝土的应力应变关系研究越来越深入，目前国内外提出的FRP约束混凝土的应力-应变模型不下数十种，本文较系统地介绍了其中几个具有代表性的FRP约束混凝土的应力-应变关系模型，并通过采用这些模型对两组试验数据的分析，做出应力-应变曲线图，由图中应力-应变曲线的对比，发现各模型间存在较大的差异。对造成这一差异的主要原因作了分析，认为主要是对影响FRP约束混凝土的力学性能的因素存在不同的认识等因素有关。

[1] Teng J G, Lam L. Behavior and Modeling of fiber reinforced poly mer-confined concrete. Journal of Structural Engineering, ASCE, 2004, 130(11): 1713-1723

[2] 于清.FRP约束混凝土柱力学性能研究[D].哈尔滨工业大学, 2002

[3] 吴刚，吕志涛.FRP约束混凝土圆柱无软化段时的应力应变关系研究[J].建筑结构学报, 2003, 24(5): 1-9

[4] Farids M N and Khalili H. FRP-encased concrete as a structural material. Magazine of Concrete Research, 1982, 34(121): 191-202

[5] Mander J B, Priestley M J N and Park R. Theoretical stress-strain model for confined concrete. Journal of Structural Engineering, 1988, 114 (8): 1804-1826

[6] Samaan M, Mirmiran A and Shahawy M. Model of concrete confined by fiber composites. Journal of Structural Engineering, 1998: 1025-1031

[7] Toutanji H. Stress-Strain characteristics of concrete columns externally confined with advanced fiber composite sheets. ACI Materials Journal, 1999, 96(3): 397-404

[8] Spoelstra M R and Monti G. FRP-confined concrete model. Journal of Composites for Construction, 1999, 3(3): 143-149

[9] Miyauchi K., Nishibayashi S. and Lnoue S. Estimation of strengthen effects with carbon fiber sheet for concrete column. Proceedings of the third international symposium on non-metallic (FRP) reinforcement for concrete structures, 1997

[10] Xiao Y. and Wu H. Compressive behavior of concrete confined by carbon fiber composite jackets. Journal of Materials in Civil Engineering, ASCE, 12(2): 139-146