基于纤维弯曲变形的粘扣带剥离强度力学模型研究

(1. 东华大学纺织面料技术教育部重点实验室，上海，201620；2. 无锡百和织造股份有限公司，无锡，201101)

粘扣带是由一条表面有细小钩子的钩面粘扣带与另一条表面有毛圈的毛面粘扣带组合构成的紧固件[1]。粘扣带作为一种概率型紧固件，可取代传统的拉链、扣子等紧固方式，广泛应用于鞋帽服饰、旅行箱包、家纺内饰、体育运动、医疗卫生、汽车电子等行业。

粘扣带的力学行为主要为剥离力和剪切力，李星[2]以假设粘扣带剥离时单钩被拉断为基础建立了粘扣带理论力学模型，并得到粘扣带剥离强度计算式。本文则试图通过粘扣带剥离时单钩弯曲部分被拉直而产生的纤维变形来建立粘扣带的剥离强度力学模型，以得到粘扣带剥离强度计算式。

1 粘扣带单钩剥离力力学模型

粘扣带剥离力主要由钩面粘扣带上的单钩钩挂毛面粘扣带上的毛圈而产生，其单钩脱离强力f的大小与粘扣带钩的材料性能(主要为纤维的弹性模量E)、粘扣带钩的单丝直径d、单钩的弯曲程度和高度等有关[3]。钩面粘扣带和毛面粘扣带的实际扣合示意如图1所示。

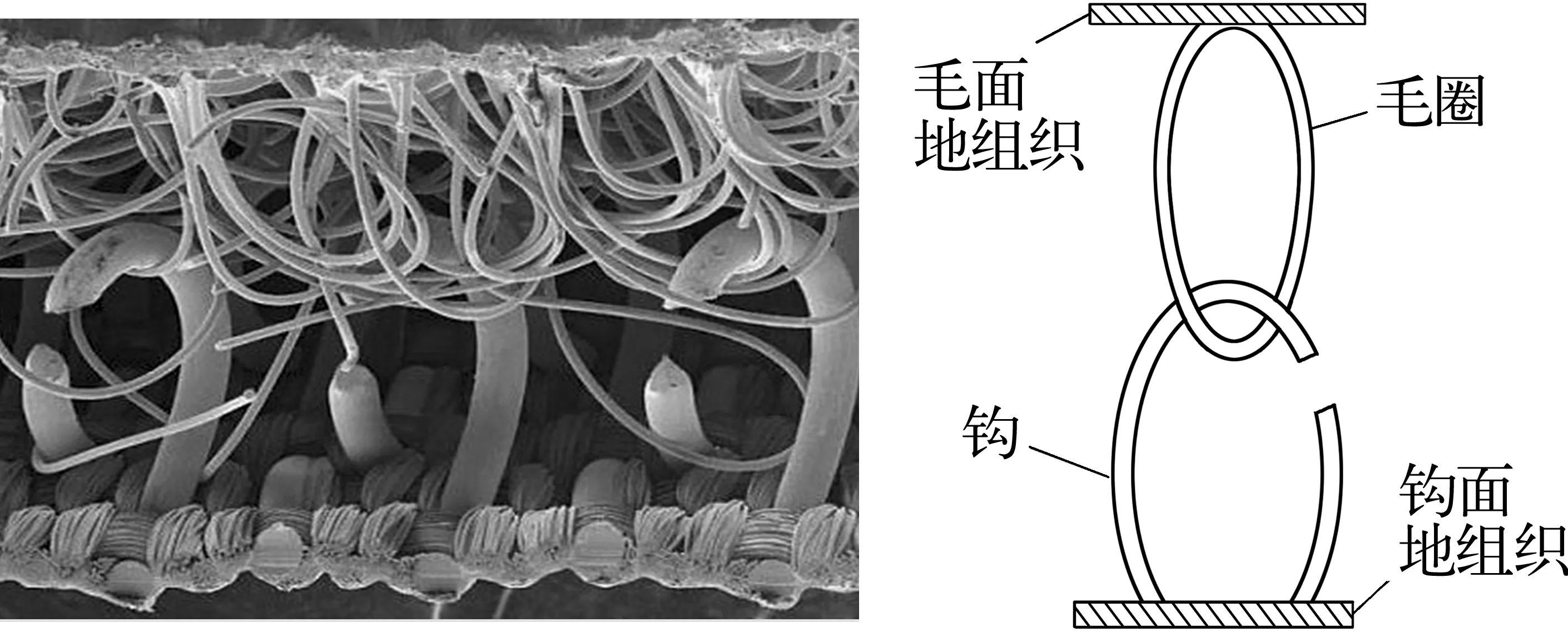
图1 钩面粘扣带和毛面粘扣带实际扣合示意图

通信作者：王其，E-mail:wq@dhu.edu.cn 粘扣带的单钩与毛圈的实际结合情况比较复杂，为简化粘扣带的力学模型,假定粘扣带的单钩力学结构模型如图2所示。其中钩面粘扣带单钩为半径R的半圆与高为h的直杆连接组成，钩与毛圈脱离时，毛圈沿直杆向上拉，直至钩从毛圈中脱出，此时力f即为单钩剥离力。又假设直杆为刚性体，不变形，此时粘扣带单钩打开的力可视为粘扣带单钩弯曲的力f，则曲率半径r0在数值上等于单钩弯曲部分半径R。

由材料力学中梁的弯曲变形公式可知[4]：

(1)

式中：M——外力矩(cN·cm)，M=fL；

f——合纤丝弯曲的力(cN)；

L——力臂长度(cm)，L=πr0；

r0——曲率半径(cm)；

E——锦纶66单丝弹性模量(cN/cm2)；

I——截面惯性矩(cm4)，I=πd4/64；

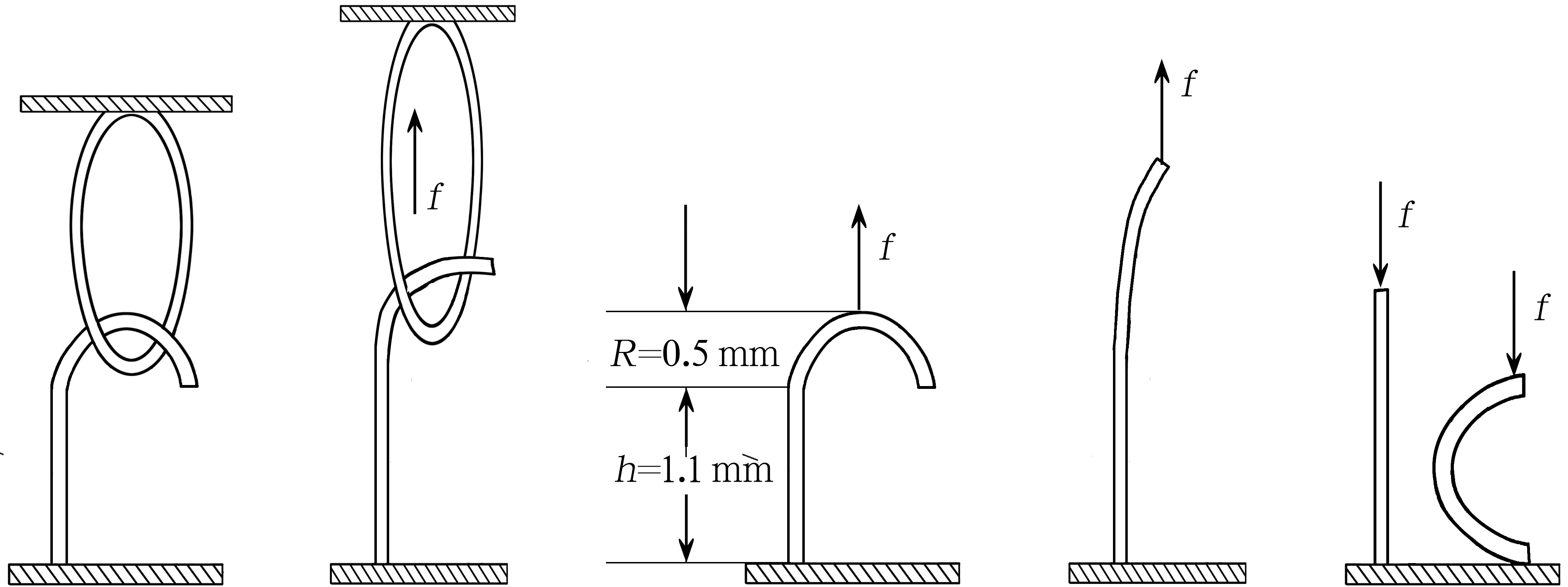
图2 粘扣带单钩剥离力学模型

d——纤维直径(cm)。

经计算整理得到粘扣带单钩剥离强力计算式：

(2)

2 单钩剥离强力力学模型的参数确定

单丝的弹性模量以实测为准，参考GB/T 14344—2003《合成纤维长丝拉伸性能试验方法》，采用AL-7000S型万能强度试验机进行等速拉伸，隔距为500 mm，拉伸速度为500 mm/min。读取应变伸长为1%和5%时的对应强力Fb、Fa。将锦纶66单丝强力—伸长曲线中伸长为1%～5%这段曲线的斜率视为该纤维的弹性模量。每个直径单丝测20次并取平均值。测试并计算所得不同直径单丝的弹性模量，如表1所示。

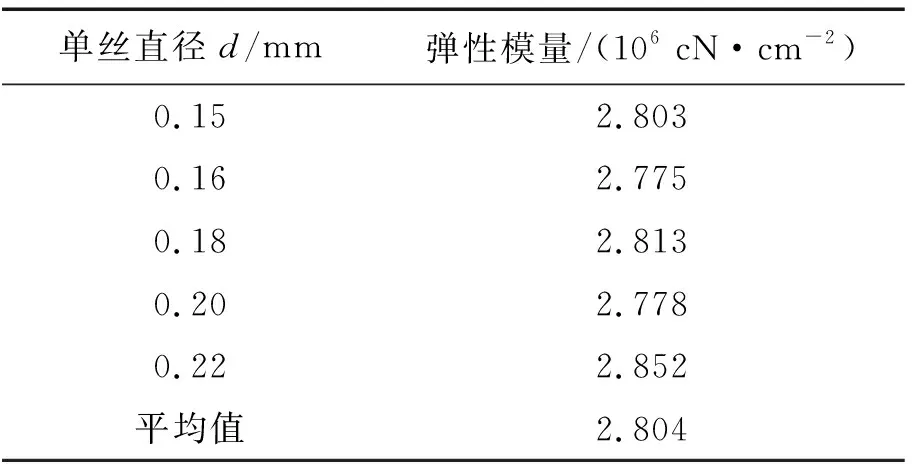
表1 锦纶66单丝的弹性模量测试值

为了预测公式的简便，取不同直径纤维弹性模量的平均值为统一弹性模量。将r0=0.05 cm，E=2.804×106cN/cm2，各单丝直径d，代入式(2)，可得理论单钩剥离强力f=1.753×107d4。各单钩理论剥离强力f计算值如表2所示。

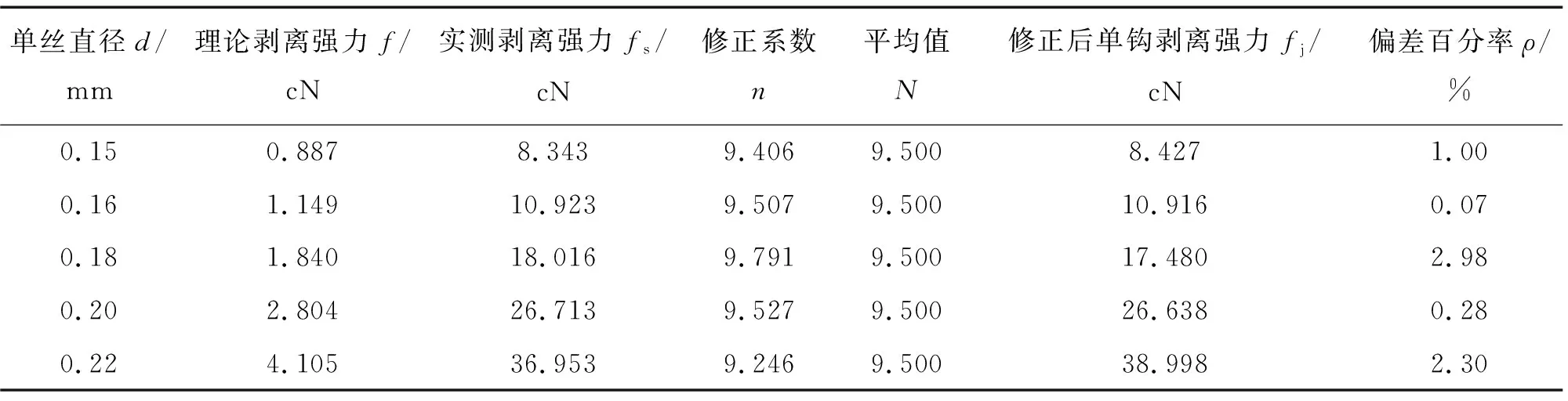
表2 粘扣带单钩的实测剥离强力、理论剥离强力及数据处理

采用LLY-06A型电子单纤强力仪对粘扣带单钩强力进行测试，注意测试时毛圈须沿单钩直杆垂直向上匀速拉伸，当粘扣带单钩与毛圈分离时，此时测得的强力值即为实测单钩剥离强力fs。实测单钩剥离强力fs为50次剥离强力的平均值，结果如表2所示。

粘扣带在织造和切钩等生产工序中经过了多次张力下的热定型，使得钩面粘扣带的钩丝刚度增大、弹性模量增加，从而使得粘扣带单钩的实测剥离强力与理论剥离强力之间产生较大的差距。为了修正这个偏差，假设实测剥离强力与理论剥离强力之间有如下关系：

(3)

式中，n为不同直径锦纶66单丝的强力修正系数。

考虑到预测公式的简便，取不同直径锦纶66单丝强力修正系数n的平均值N作为最终修正系数，从而可得修正后的单钩理论剥离强力fj(计算结果如表2所示)：

fj=Nf

(4)

进一步检验修正后的理论单钩剥离强力相对于实际单钩剥离强力的偏差百分率ρ[式(5)]：

(5)

计算所得偏差百分率见表2。由表2可知，偏差百分率ρ<3%，偏差控制在较小的范围内。

综上所述，粘扣带单钩剥离强力预测公式可以表示为：

(6)

式中：f——粘扣带单钩剥离强力(cN)；

N——强力修正系数，取平均值N=9.5；

E——锦纶66单丝弹性模量(cN/cm2)，E=2.804×106cN/cm2；

d——粘扣带钩丝直径(cm)；

r0——粘扣带钩丝曲率半径(cm)，r0=0.05 cm。

3 粘扣带剥离强度力学模型的建立

基于上文得到的粘扣带单钩剥离强力模型以及粘扣带单钩剥离强力计算式，对整片粘扣带强力进行计算及预测，尝试建立单位宽度粘扣带的剥离强力力学模型。

假设在一整片粘扣带中，钩面粘扣带单位宽度上钩的数量即钩密度为M(钩/cm)，钩面粘扣带和毛面粘扣带扣合时的有效宽度为W(cm)，钩面粘扣带成功钩挂在毛面粘扣带上的百分率为钩挂率ω(%)。由于钩面粘扣带和毛面粘扣带在剥离过程中，第一排毛圈与第一排钩还未完全脱离时，后排钩与对应排毛圈也开始剥离并对剥离强力产生贡献，造成牵连关系，这就需要在该力学模型中用修正系数k(常数)加以修正，从而得到整片粘扣带剥离强度P的计算式：

P=kωWMf

(7)

4 粘扣带剥离强度模型参数的确定

在实际粘扣带扣合过程中，不同单丝直径的钩面粘扣带与毛面粘扣带的宽度W、钩密度M、钩挂率ω如表3所示。

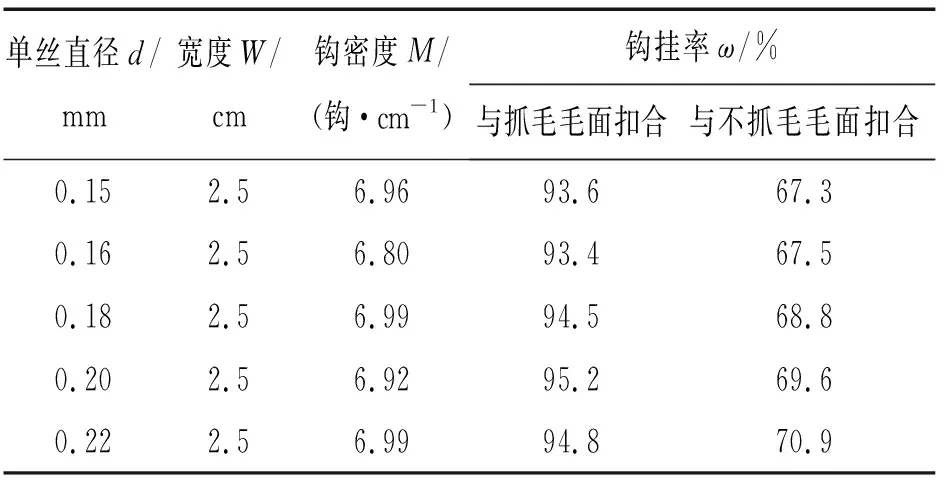
表3 粘扣带的宽度、钩密度和钩挂率

为使计算式简单易用，取钩密度M=7钩/cm，抓毛毛面粘扣带的钩挂率ω= 95%，不抓毛毛面粘扣带的钩挂率ω= 70%。当修正系数k=1时，表示第一排毛圈与第一排钩脱离过程中，后排钩与对应排毛圈并未对剥离强度产生贡献。将以上各参数代入式(7)，可得修正系数k=1时，钩面粘扣带与抓毛毛面粘扣带和不抓毛毛面粘扣带扣合理论剥离强度P，如表4和表5所示。

参照GB/T 23315—2009《粘扣带》测试剥离强度,将试样裁切成100 mm×25 mm钩面粘扣带和毛面粘扣带组成试样，在AL-7000S型万能强度试验机上测试，隔距为40 mm，拉伸速度为200 mm/min。最终的剥离强度试验值为5组剥离强度平均值。钩面粘扣带与抓毛毛面粘扣带和不抓毛毛面粘扣带扣合的实测剥离强度Ps如表4和表5所示。

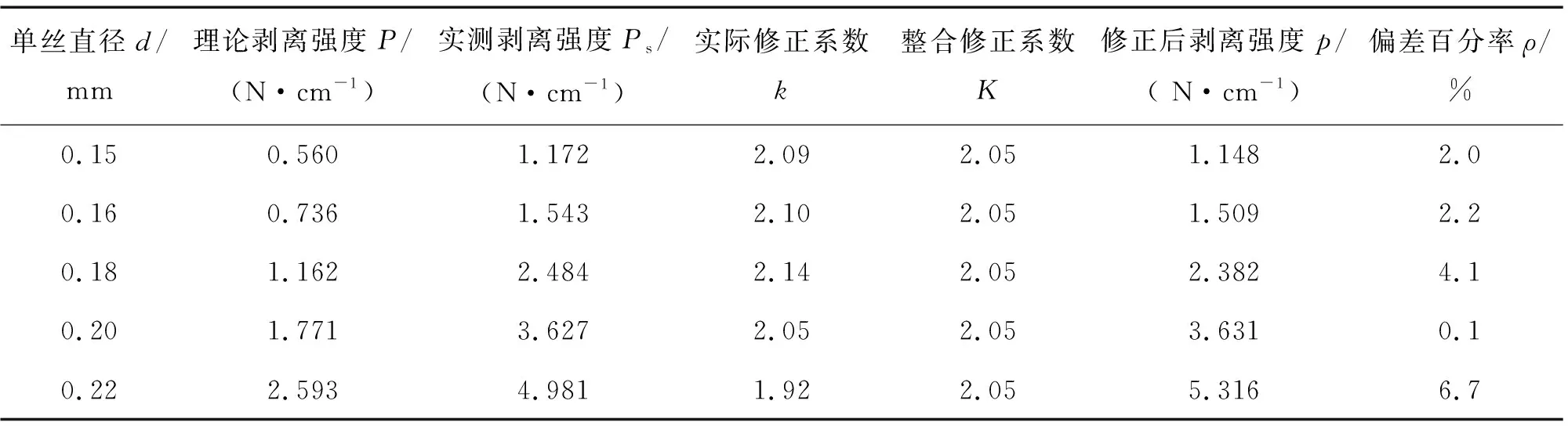
表4 钩面粘扣带与抓毛毛面粘扣带的理论剥离强度、实测剥离强度及数据处理

而实际修正系数k>1，并且为了减少强力模型中参数的数量，定义实际修正系数k不仅可修正第一排毛圈与第一排钩脱离过程中，后排钩与对应排毛圈对剥离强度产生的贡献，同时还可修正钩面粘扣带不同直径钩的钩密度M和粘扣带钩毛的钩挂率ω的差异。实际修正系数k可用实测剥离强度Ps与理论剥离强度P的比值得出，即：

(8)

实际修正系数k的计算结果如表4和表5所示。

为了预测公式的简便性和扩大模型的代表性，对不同直径单丝的实际修正系数k进行整合，整合修正系数为K。对于钩面粘扣带和抓毛毛面粘扣带扣合，取K=2.05；对于钩面粘扣带与不抓毛毛面粘扣带扣合，取K=1.94。修正后的剥离强度p的计算结果如表4和表5所示。

为验证简化计算式的有效性，可通过计算在简化计算式中的理论剥离强度相对于实际剥离强度的偏差百分率ρ[式(9)]来验证，并约定偏差百分率在一定范围内时，简化K值是有效的，简化后的计算式预测精度能符合实际需要。

(9)

式中：p——修正后的理论剥离强度(N/cm)；

Ps——实测剥离强度(N/cm)。

将K代入式(7)得到理论强度p后，与实测剥离强度Ps代入式(9)，所得剥离强度的偏差百分率ρ如表4和表5所示。

由表4可知，钩面粘扣带与抓毛毛面粘扣带剥离强度的偏差百分率ρ<7%；由表5可知，钩面粘扣带与不抓毛毛面粘扣带剥离强度的偏差百分率ρ<4%。说明简化后的粘扣带剥离强度计算公式在允许偏差范围内是有效的，可以用于粘扣带剥离强度的计算和预测。

最终整片粘扣带剥离强度理论公式可表示为：

(10)

修正后的整片粘扣带剥离强度计算式为：

抓毛毛面粘扣带与钩面粘扣带扣合时

p=22.7×108d4(cN/cm)

(0.015 cm≤d≤0.022 cm)

(11)

不抓毛毛面粘扣带与钩面粘扣带扣合时

p=15.83×108d4(cN/cm)

(0.015 cm≤d≤0.022 cm)

(12)

5 结语

以材料弯曲变形为基础建立粘扣带单钩剥离强力力学模型，进而建立粘扣带剥离强度力学模型。从粘扣带剥离强度计算式可知，影响粘扣带剥离强度的因素包括粘扣带钩的材料性能(主要为纤维的弹性模量E)、粘扣带钩的直径d、钩的密度M、钩挂率ω和整合修正系数K等。

对粘扣带剥离强力力学模型中的参数进行修正，由此得到粘扣带剥离强度的简单计算式，在偏差百分率7%以内，可以用于粘扣带剥离强度的计算和预测。

该粘扣带剥离强度模型建立在纤维弯曲变形的基础上，所模拟的力学行为与实际粘扣带剥离行为更符合实际，用一个公式可以计算和预测单钩直径在较大范围变化的粘扣带的剥离强度，也有明显进步。

[1] 郑森煤.粘扣带: 中国,200973428[P].2007-11-14.

[2] 李星,王其.粘扣带剥离强度力学模型研究[J].产业用纺织品,2011,29(10):19-22.

[3] WILLIAMS J A, DAVIES S G, FRAZER S. The peeling of flexible probabilistic fasteners[J]. Tribology Letters,2007,26(3):213-222.

[4] 于伟东.纺织材料学[M].北京:中国纺织出版社,2006:115.