纽结的Homflypt多项式
霍承刚
宿州学院数学与统计学院,安徽宿州,234000
纽结的Homflypt多项式
霍承刚
宿州学院数学与统计学院,安徽宿州,234000
介绍了一类重要的纽结不变量,即Homflypt多项式,证明了两个环链的Homflypt多项式相等的必要条件是它们的环绕数相等。此外,研究了它同纽结Jones多项式和Vassiliev不变量之间的关系。
纽结;环链;Vassiliev不变量;Jones多项式;Homflypt多项式
纽结理论就是研究纽结与环链在连续变形下保持不变的特性(称为不变量),其目的在于告诉人们如何区分不同的纽结。由于纽结与环链既直观又充满奥妙,纽结理论既通俗易懂、妙趣横生,而又有极其深刻的内涵,并且与分子生物学、理论物理等自然科学领域密切相关。1984年,Jones发现的Jones多项式是一种同痕不变量,计算方便,它的发现使得纽结理论成为世界数学界注意的焦点之一[1-3]。之后,其他数学家又将这些多项式加以推广,如Homflypt多项式等。
1 预备知识
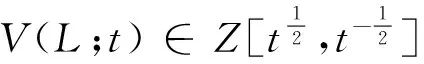
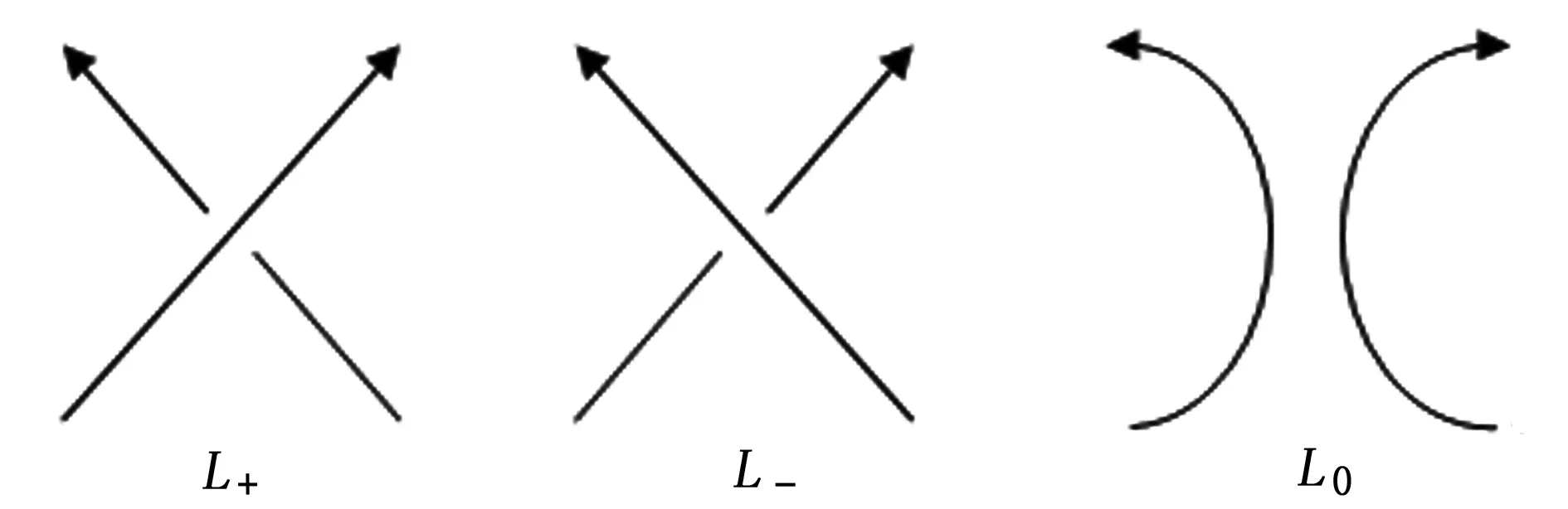
图1
(2)V(Ο;t)=1,其中Ο为平凡纽结。
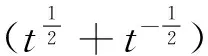
定义2 令PL(v,z)表示环链L的Homflypt多项式,它有下列关系式定义:
(1)v-1PL+(v,z) —vPL—(v,z) =zPL0(v,z);
(2)PΟ(v,z)=1,其中O表示平凡纽结。
对值域为阿贝尔群的纽结不变量,可以通过下述线束关系:
v(KD)=v(K+)-v(K-)
定义奇异纽结的不变量,其中KD,K+,K-表示除一个交叉点外其余部分是完全相同的纽结图表(图2)。
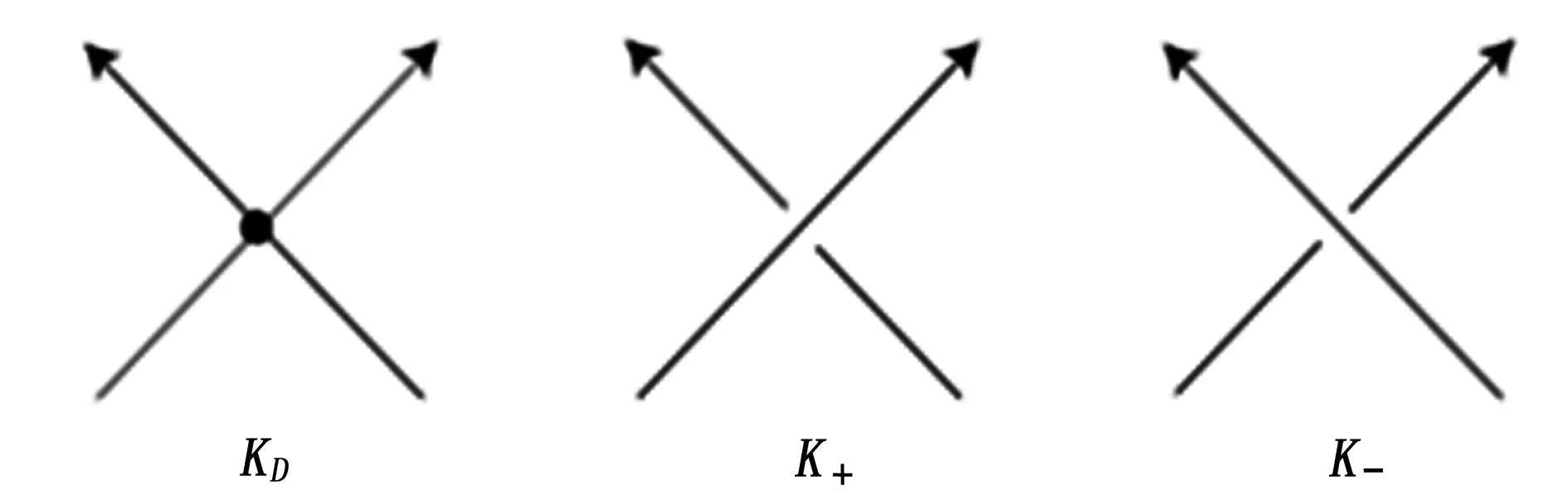
图2
定义3 设v为值域在阿贝尔群的纽结不变量,如果对任意多于n个奇异点的纽结K有v(K)=0,则称此不变量为n阶(Vassiliev)不变量,通常记为vn。
引理1 设L=K1∪K2,L′=K1′∪K2′是两个分支的环链,VL(t),VL′(t)分别表示L和L′的Jones多项式,记λ=Link(K1∪K2),λ′=Link(K1′∪K2′)分别为两个环链的环绕数,则VL(t)=VL′(t)的必要条件是λ=λ′。
2 与琼斯多项式的关系
一方面,Jones多项式容易计算,有很强的识别不同纽结的能力,它甚至可以识别三叶结和它的镜面像;另一方面,找到了纽结理论与理论物理(主要是量子统计力学、量子场理论)的结合点,这不但大大推动了理论物理学的发展,反过来物理学家也为数学发展作出了贡献,提出了一系列的纽结不变量;另外,利用Jones多项式解决了许多纽结理论中长期悬而未决的困难问题。
定理1 设L=K1∪K2,L′=K1′∪K2′是两个分支的环链,记λ=Link(K1∪K2),λ′=Link(K1′∪K2′)分别为两个环链的环绕数,而PL(v,z),PL′(v,z)分别表示L和L′的Homflypt多项式,则PL(v,z)=PL′(v,z)的必要条件是λ=λ′。
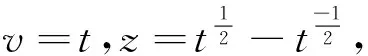
若L和L′的Homflypt多项式相等,即PL(v,z)=PL′(v,z),从而VL(t)=VL′(t)。根据引理1立知λ=λ′。

3 与Vassiliev不变量的关系
Vassiliev不变量被证明至少同Jones多项式及其源于各种量子群的一般形式具有同等作用[1]。
定理2 设环链L的Homflypt多项式为:


此定理还有另外一种证明方法[5]。
Homflypt多项式的一种标准形式是以q和N为参数的多项式,且满足下列等式:


上式为关于x的“一团”的表达式,其中“一团”表示此部分比较复杂,但不管它是什么,此时多项式的系数是有限阶的。
4 结束语
虽然纽结的Jones多项式及Homflypt多项式对纽结的分类起着重大作用,但它们已被证明不是纽结的完全不变量。纽结的Vassiliev不变量被证明至少同Jones多项式及其源于各种量子群的一般形式具有同等作用,对Vassiliev不变量的判定研究正在展开,相信将对纽结的研究产生重要意义。------------
[1]Barnatan D.On the Vassilliev knot invariants[J].Topology,1995,34:423-472
[2]Zhu J.On Jones knot invariants and Vassiliev invariants[J].J Math,1998,27(2):293-299
[3]Kofman I.Approximating Jones coefficients and other link invariants by Vassiliev invariants[J].Journal of knot theory and its ramifications,2000,9(7):955-966
[4]李东升.环链的多项式不变量相等之必要条件[J].湖北大学学报,1992,14(4):338-341
[5]霍承刚.纽结的Vassiliev不变量[D].大连:辽宁师范大学,2007:7-8
(责任编辑:汪材印)
Homflypt Polynomials of Knots
HUO Cheng-gang
School of Mathematics and Statistics,Suzhou University,Suzhou Anhui,234000,China
The paper introduces the useful instrument of knot theory——Homflypt Polynomials.The paper proves that the necessary condition for two links to have same Homflypt polynomials is same link number. Furthermore, its relationship with Jones polynomials and Vassiliiv invariant is aslo introduced.
knot;link;vassiliiv invariant;Jones polynomials; Homflypt polynomials
2014-05-28
安徽省高校省级自然科学研究项目“纽结的Vassiliev不变量性质及应用”(KJ2013Z321)。
霍承刚(1980-),山东德州人,硕士,讲师,主要研究方向:低维拓扑。
10.3969/j.issn.1673-2006.2014.09.021
O189
A
1673-2006(2014)09-0072-02

