毛毛虫图的r次幂的最小斜秩

沈小玲，候辉平

(湖南师范大学数学与计算机科学学院，中国 长沙 410081)

毛毛虫图的r次幂的最小斜秩

沈小玲*，候辉平

(湖南师范大学数学与计算机科学学院，中国 长沙 410081)

图的最小斜秩问题是确定图的所有斜对称矩阵在域F上的秩的最小值.利用构造矩阵和零强迫集的方法刻画了毛毛虫图的r次幂的最小斜秩.设毛毛虫Tn有n个节点,n和r都是正整数，r是奇数，那么

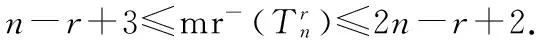
最小斜秩；斜对称矩阵；毛毛虫图的r次幂

设G是一个无环无重边的简单图,顶点集为V(G),边集E(G).用|G|表示G的顶点数.顶点v的度数用dG(v)(或d(v))表示.度为k的顶点也叫k-顶点.度为1的顶点叫悬挂点.若树图中恰有一个度大于2的顶点，则这棵树叫做似星树.设集合S⊆V,由S导出的子图记为G[S].若S仅包含一个顶点v,则用G-v代替G-S.图G的j次幂是指图Gj=(V,F),边{u,v}∈F当且仅当存在u到v长为j的路.

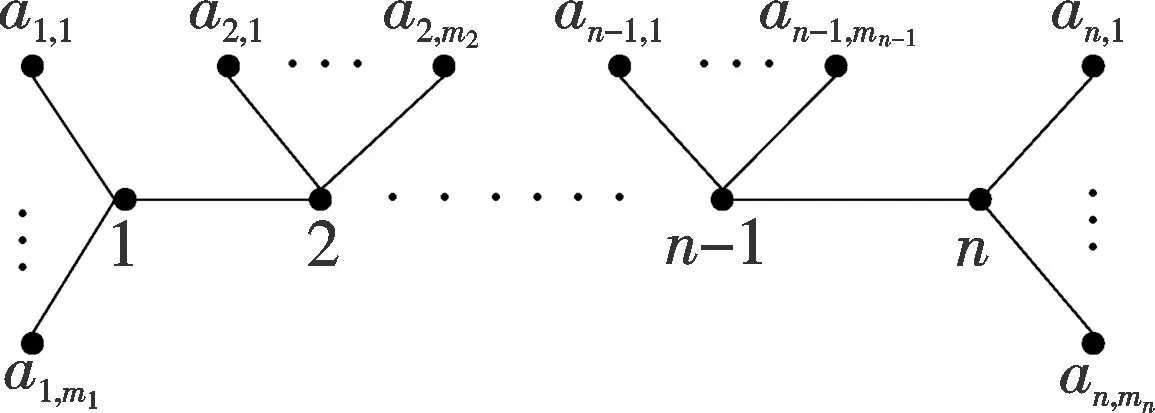
图1 毛毛虫TnFig.1 Caterpillar Tn

在路的节点上加悬挂边所得的图就是毛毛虫图.在本文中，除特别说明，我们规定每条毛毛虫至少有2个非悬挂点.这些非悬挂点称为节点.设Tn是一颗有n个节点的毛毛虫.一条毛毛虫是正则的是指直径路P中没有两个连续的顶点的关节，否则称为不正则的.设毛毛虫的节点i有mi条脚，标记为ai,1,…,ai,mi,i∈{1,…,n},如图1所示；m1,mn≥1,mj≥0,j∈{2,3,…,n-1}.

1 预备知识

域F上的由图G所描述的斜对称矩阵的集合

S-(F,G)={A∈Fn×n:AT=-A；G(A)=G}.

图G在域F上的最小斜秩(minimum skew-rank)定义为：mr-(F,G)=min{rankA:A∈S-(F,G)}.图G在域F上最大斜零度定义为：M-(F,G)=max{null(A):A∈S-(F,G)}.显然，mr-(F,G)+M-(F,G)=|G|.图G的最大斜秩是指：MR-(F,G)=max{rankA:A∈S-(F,G)}.有关最小秩和斜秩的研究及背景见参考文献[1～13].

定义1[11]设图G=(V，E).

设Z是V的子集，若将Z中的所有点都着黑色，不在Z中的点都着白色，则称集合Z是初始颜色集.

斜颜色改变规则是指：如果V中的顶点v恰有一个着白色的与之相邻的顶点w,将w的颜色变成黑色.这种情况下，我们说v强迫w.

给定一个初始颜色集Z，将Z应用斜颜色改变规则对顶点改变颜色，直到V中没有顶点的颜色可以改变，所得的最终结果叫做Z的斜导出色集.

一个斜零强迫集是指子集Z⊆V的导出色集是V.

斜零强迫数Z(G)是指斜零强迫集的最小元素个数.

引理1[11]对任意图G和任意域F，M-(F,G)≤Z-(G),mr-(F,G)≥|G|-Z-(G).

以下是关于匹配和最小斜秩的一些已知的结果.

引理2[11]给定图G.

(1)域F上的任何最小斜秩都是偶数.

(2)在mr-(G)和MR-(G)之间的任意偶秩都能实现.

(3)mr-(G)=|G|当且仅当G有唯一完美匹配.

(4)MR-(G)=2match(G).

(5)如果T是一颗树，那么mr-(T)=2match(T)=MR-(T).

(6)mr-(G)=2当且仅当G是完全多部图.

(7)如果H是G的一个导出子图，那么mr-(H)≤mr-(G).

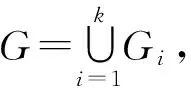
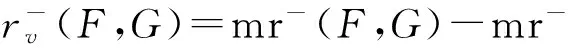
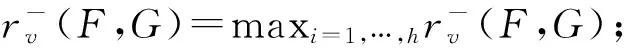
引理4[12-13]设n和r是正整数，n≥3,

(1)如果r是奇数，那么

(2)如果r=2s，那么

2 主要结论

本节我们主要研究毛毛虫的k次幂的斜对称矩阵的最小秩.为方便，我们将斜对称矩阵的最小秩简称为最小斜秩.

引理5设毛毛虫Tn有n个节点，n和r都是正整数,r≥n,那么

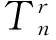
定理1设毛毛虫Tn有n个节点，n和r都是正整数，r是奇数，那么

证将毛毛虫的除了最后一个悬挂点外，其余的悬挂点都变成黑色，同时将前r-1个节点变成黑色.则这些黑点所构成的集合是毛毛虫的零强迫集，其零强迫顺序链为：

a1,1→r,1→r+1,…,n-r→n,n-r+1→an,mn.

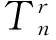
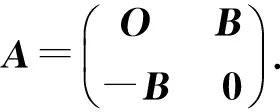
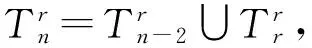
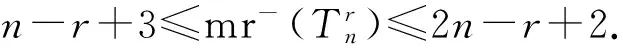
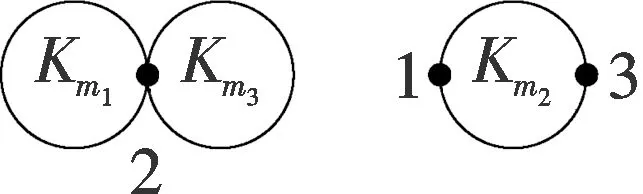
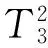
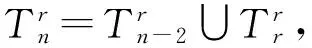
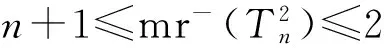
证设n=2s+1,x=2t.如果Tn的前2(s-t)-1个节点的度数都不小于3，而其余节点的度数都为2(见图3).为方便，图中仅以2(s-t)-1个3-度顶点来代替度数都不小于3的顶点.

图3 有2(s-t)-1个3-度节点其余节点度为2的毛毛虫Tn及Fig.3 Caterpillar Tn and with 2(s-t)-1 3-degree vertices, the rest vertices are all of degree 2

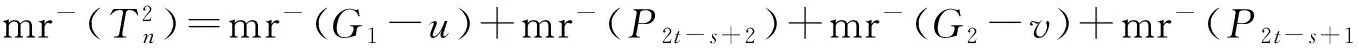
同理可证下面定理.

当毛毛虫Tn只有第一个节点的度大于2，即Tn为图4中的Sm.不妨设有c个悬挂点与顶点1相邻.我们有如下结论.

性质2对于图Sr,r为偶数，

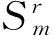
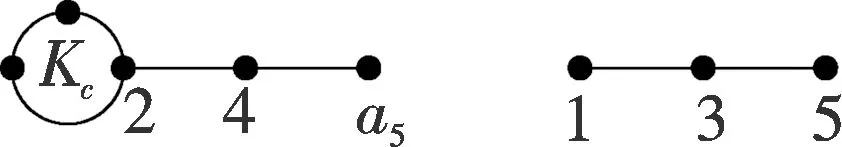
图4 图

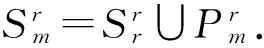
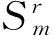
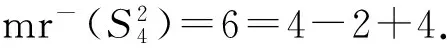
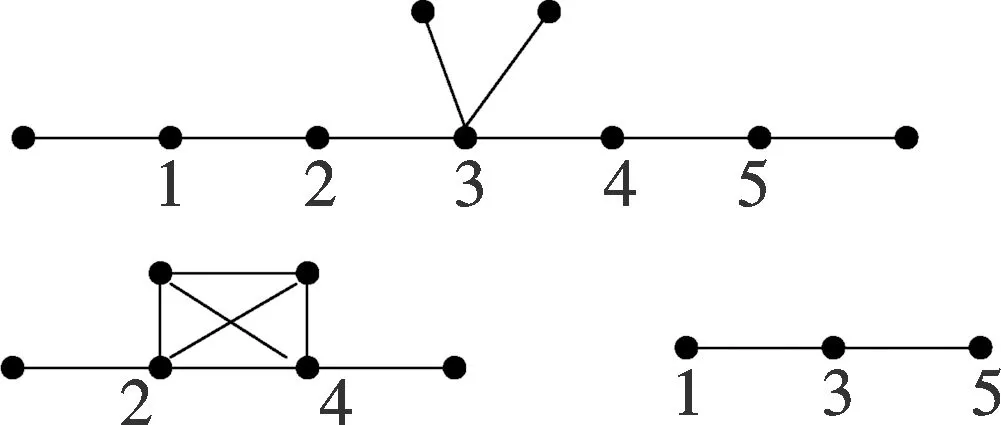
图5 毛毛虫T5和它的2次幂.Fig.5 Caterpillar T5 and its 2-power

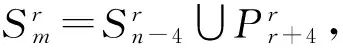
如果毛毛虫的第一个和最后一个节点度大于2，记为图Wm，那么

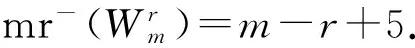
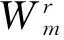
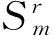
同理可证，

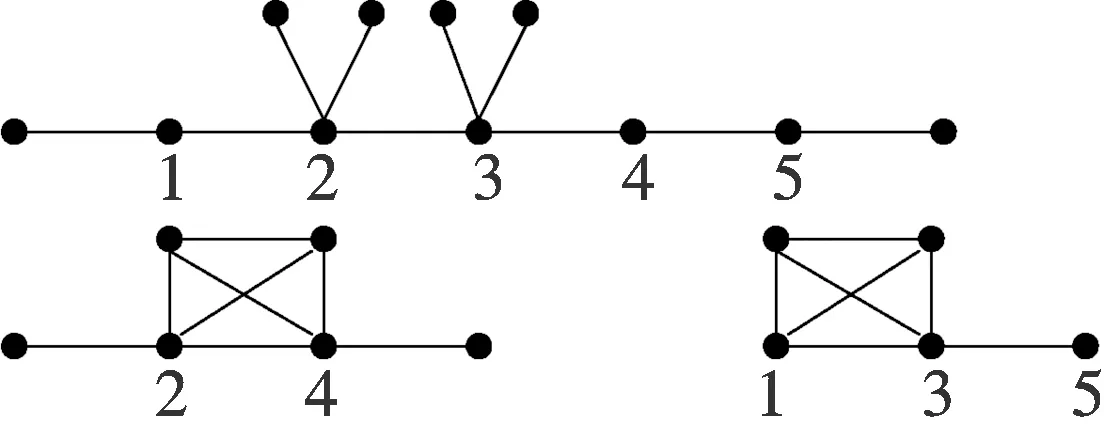
图6 图T5及

性质4对于图Wm,当m为偶数时,

[1] BARIOLI F, BARRETT W, BUTLER S,etal. Zero forcing sets and the minimum rank of graphs[J]. Linear Algera Appl, 2008,428(7):1628-1648.

[2] BERMAN A, FRIEDLAND S, HOGBEN L,etal. An upper bound for the minimum rank of a graph[J]. Linear Algera Appl, 2008,429(7):1629-1638.

[3] BARIOLI F, FALLAT S M, HERSHKOWITZ D,etal. On the minimal rank of not necessarily symmetric matrices: a preliminary study[J]. Electron J Linear Algebra, 2009,18:126-145.

[4] BARRETTE W, VAN DER HOLST H, LOEWY R. Graphs whose minimalrank is two[J]. Electron J Linear Algera, 2004,11:258-280.

[5] BARRETTE W, VAN DER HOLST H, LOEWY R. Graphs whose minimalrank is two: the finite fields case[J]. Electron J Linear Algebra, 2005,14:32-42.

[6] BARRETTE W, GROUT J, LOEWY R. The minimal rank problem over the finite field of order 2:minimum rank 3[J]. Linear Algebra Appl, 2009,431(4):890-923.

[7] DEALBA L, GROUT J, HOGBEN L,etal. Universally optimal matrices and field indepence of the minimum rank of a graph[J]. Electron J Linear Algebra, 2009,18:403-419.

[8] FALLAT S M, HOGBEN L. The minimum rank of symmetric matrices described by a graph: a survey[J]. Linear Algera Appl, 2007,426(2-3):558-582.

[9] HOGBEN L. Minimum rank problems[J]. Linear Algera Appl, 2010,432(8):1961-1974.

[10] SHEN X, HOU Y, SHENG L. On the minimum rank of third power of a starlike tree[J]. Linear Algera Appl, 2012,436(12):4503-4511.

[11] ALLISON M, BODINE E, DEALBA L M,etal. Minimum rank of skew-symmetric matrices described by a graph[J]. Linear Algebra Appl, 2010,432(10):2457-472.

[12] DEALBA L, KERZNER E, TUCKER S. A note on the minimum skew rank of powers of paths[EB/OL]. http://cn.arxiv.org/abs/1107.2450v1.

[13] 盛 立.图的最小反秩[D].长沙：湖南师范大学硕士学位论文, 2011.

(编辑 沈小玲)

Minimum Skew-Rank ofr- Power of Caterpillars

SHENXiao-ling*,HOUYao-ping

(College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)

The minimum skew-rank of a simple graphGis the smallest possible rank among all skew-symmetric matrices overF. The minimum skew-rank ofr-power of caterpillar is characterized by using constructing matrices and zero-forcing. LetTnbe a caterpillar, andn,rare all positive integers,ris odd, then

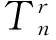
minimum skew-rank; skew-symmetric matrix;r-power of caterpillars

2014-04-20

国家自然科学基金资助项目(10771061);湖南省自然科学基金资助项目(14JJ7036)

*

,E-mail：185869458@qq.com

O151.21

A

1000-2537(2014)04-0087-05