单轴拉伸和压缩镁合金各滑移系的Schmid因子计算

娄 欢，万 刚，武保林

(沈阳航空航天大学 材料科学与工程学院，沈阳 110136)

单轴拉伸和压缩镁合金各滑移系的Schmid因子计算

娄 欢，万 刚，武保林

(沈阳航空航天大学 材料科学与工程学院，沈阳 110136)

针对单轴拉伸和压缩条件下的镁合金，计算了不同滑移系(基面滑移、柱面滑移、锥面滑移、锥面滑移)在整个取向空间中的Schmid因子分布。计算结果表明，基面滑移、柱面滑移和锥面滑移系的Schmid因子在取向空间中都有0.5的极大值；而锥面滑移系的Schmid因子普遍较低，当θ在80°左右，Ψ在70°左右时的最大值仅为0.383。计算结果为镁合金变形机制的分析提供基础。

Schmid因子；滑移系；镁合金

Schmid定律是研究晶体塑性变形规律与特点的一个非常重要的定律[1-4]。对于同一类金属来说，只要其纯度、加工处理状态等相同，同一滑移系启动所需要的临界剪切应力就是一个定值[5-6]，对于镁合金塑性变形机制的确定，更多的是需要考虑Schmid因子的大小。作为一个重要的参数，Schmid因子经常用来分析镁合金在不同取向条件下变形机制的可能性。因此，单轴拉伸压缩条件下镁合金位错Schmid因子的计算，对镁合金在该条件下微观变形机制的讨论分析有着明显的参考作用[7-9]。本文以镁合金为对象，计算在单轴拉伸压缩条件下镁合金各滑移系的Schmid因子在取向空间中的分布，以期为变形机制的分析提供基础。

1 计算过程

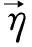
m=|cosφcosλ|

(1)

其中，φ是载荷作用方向与滑移面法向之间的锐角；λ是载荷作用方向与滑移方向之间的夹角。在单向拉伸压缩时，晶粒中位错滑移的Schmid因子分布可以通过确定载荷轴在取向三角区域内(图1中高亮灰色的部分)的取向，然后利用公式(1)计算得到。

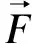
(2)

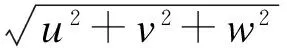
(3)

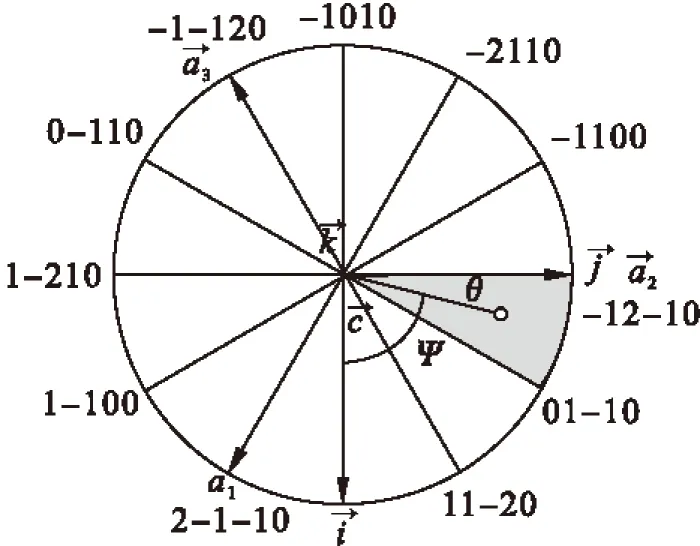
图1 冲击载荷方向轴在取向空间中位置示意图

或者是

SF=|cosα|·|cosλ|

(4)

SF=|cosα||cosλ|

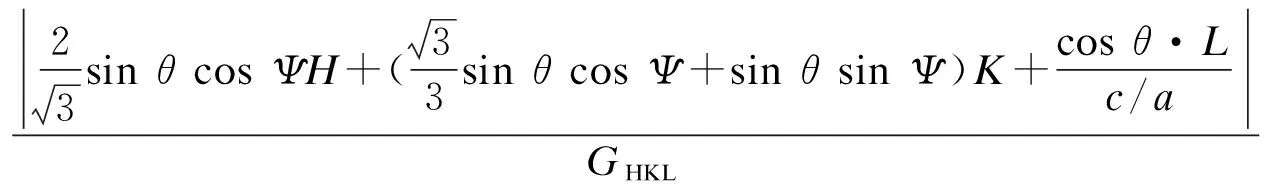
(5)

其中，c/a是镁合金的轴比值，H、H和L为滑移面的米勒指数，U、V和W是滑移切变方向矢量η1的米勒指数，θ和Ψ值分别在0°～90°和60°～90° 范围。对应Schmid因子计算公式(5)，可编制相应的计算程序，并绘制出相应的Schmid因子分布图。

2 计算结果及讨论分析

图2分别给出了基面滑移(图2(a))、柱面滑移(图2(b))、锥面滑移(图2(c))与锥面滑移(图2(d))在Ψ=60°时的Schmid因子随θ变化曲线，也就是<0001>-<01-10>取向线上Schmid因子的分布。

从图2(a)中可以看出，沿着<0001>-<01-10>取向线，3个基面滑移系中(0001)[11-20]和(0001)[1-210]的Schmid因子相等，而(0001)[2-1-10]的Schmid因子恒为0；对于柱面滑移(图2(b))的三个滑移系，(1-100)[11-20]和(10-10)[-12-10]的Schmid因子相等，而(0-110)[2-1-10]的Schmid因子恒为0；在锥面滑移(图2(c))6个滑移系中，(1-101)[11-20]和(-1011)[1-210]、(10-11)[-12-10]和(-1101)[-1-120]、(01-11)[-2110]和(0-111)[2-1-10]的Schmid因子分别相等，其中(01-11)[-2110]和(0-111)[2-1-10]的Schmid因子恒为0；对于锥面滑移(图2(d))6个滑移系，(11-22)[-1-123]和(-12-12)[1-213]、(1-212)[-12-13]和(-1-122)[11-23]、(2-1-12)[-2113]和(-2112)[2-1-13]分别相等。只有2个锥面滑移系有0.5的最大值，基面和柱面滑移系都分别有两组滑移系最大值为0.45，锥面滑移系的Schmid值较小。

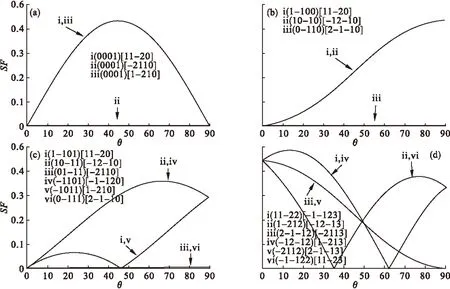
图2 Ψ=60° 时的Schmid因子曲线

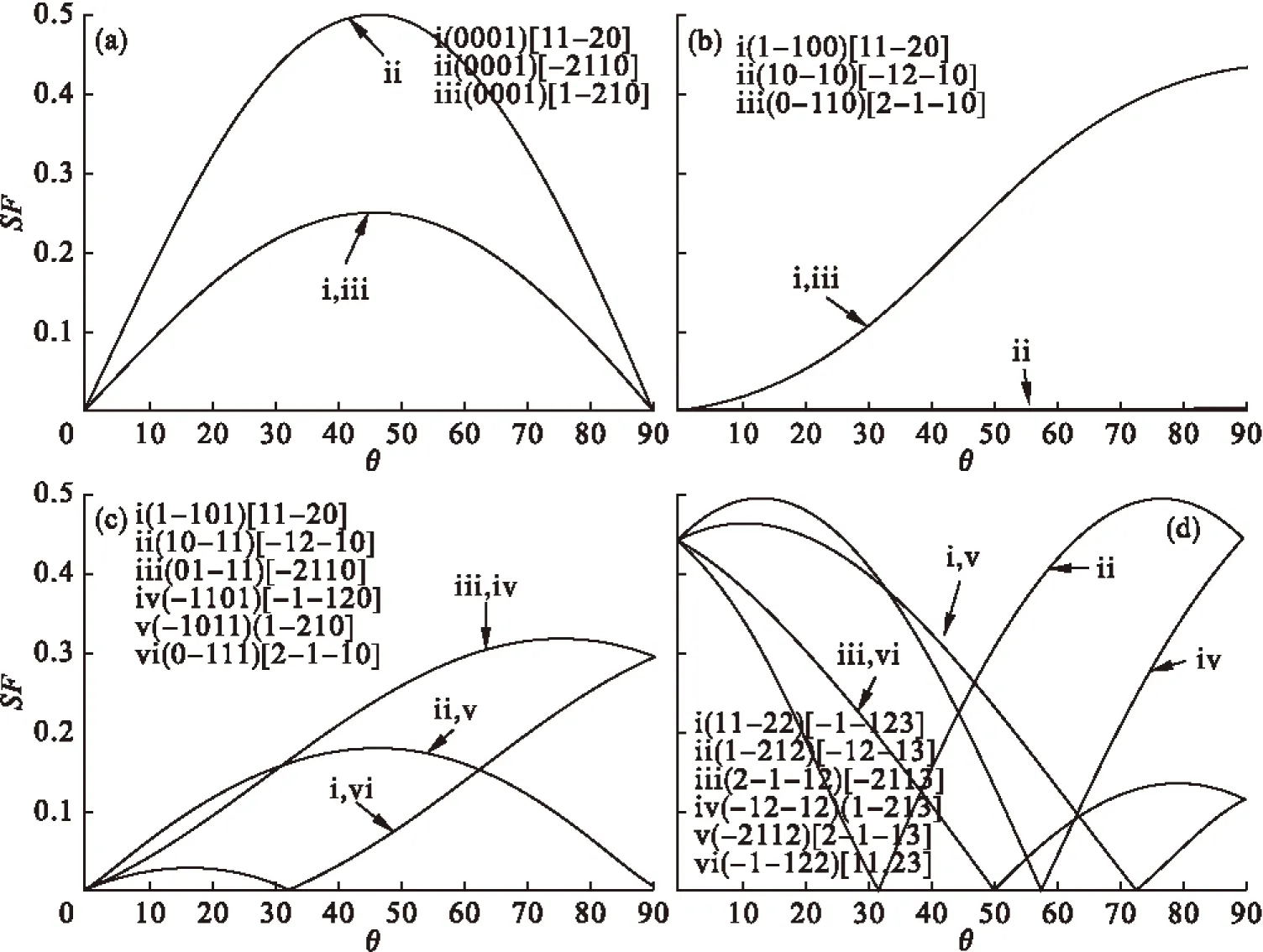
图3 Ψ=90°时的Schmid因子曲线

图3分别为基面滑移(图3(a))、柱面滑移(图3(b))、锥面滑移(图3(c))与锥面滑移(图3(d))在Ψ=90(时的Schmid因子随(变化曲线，也就是沿着<0001>-<-12-10>取向线上Schmid因子的分布。

从图3(a)中可以看出，当Ψ=90(时，沿着<0001>-<-12-10>线，3个基面滑移系中(0001)[11-20]和(0001)[1-210]的Schmid因子相等，而(0001)[2-1-10]的Schmid 因子有最大值0.5；在柱面滑移(图3(b))3个滑移系中，(1-100[11-20]和(0-110)[2-1-10]的Schmid因子相等，(10-10)[-12-10]的Schmid因子恒为0；在锥面滑移(图3(c))6个滑移系中，(1-101)[11-20]和(0-111)[2-1-10]、(10-11)[-12-10]和(-1011)[1-210]、(01-11)[-2110]和(-1101)[-1-120]的Schmid因子分别相等；在锥面滑移(图3(d))6个滑移系中，(11-22)[-1-123]和(-2112)[2-1-13]、(2-1-12)[-2113]和(-1-122)[11-23]和分别相等，而锥面滑移(-12-12)[1-213]、(1-212)[-12-13]的Schmid 因子有最大值0.5。

图2和图3只是反映了在特定的角度下的各滑移系的Schmid因子值的变化，而将Ψ和θ角度值在各自范围内变化，得到在整个取向空间的Schmid因子的分布更具普适意义。本文采用等高线方式，根据上面Schmid因子计算公式来绘制出取向空间的分布图，根据Schmid因子值的大小变化，颜色由蓝色到红色逐渐的递增，如图4-图7所示。由于滑移没有方向的限制，所以Schmid因子都为正值，最大和最小的Schmid因子值分别为0.5和0。

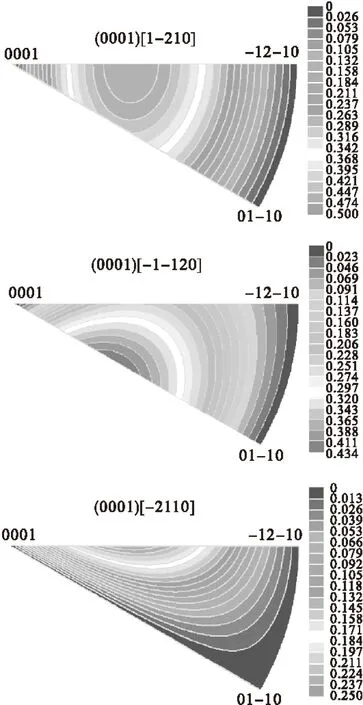
图4 基面滑移系的Schmid因子分布图

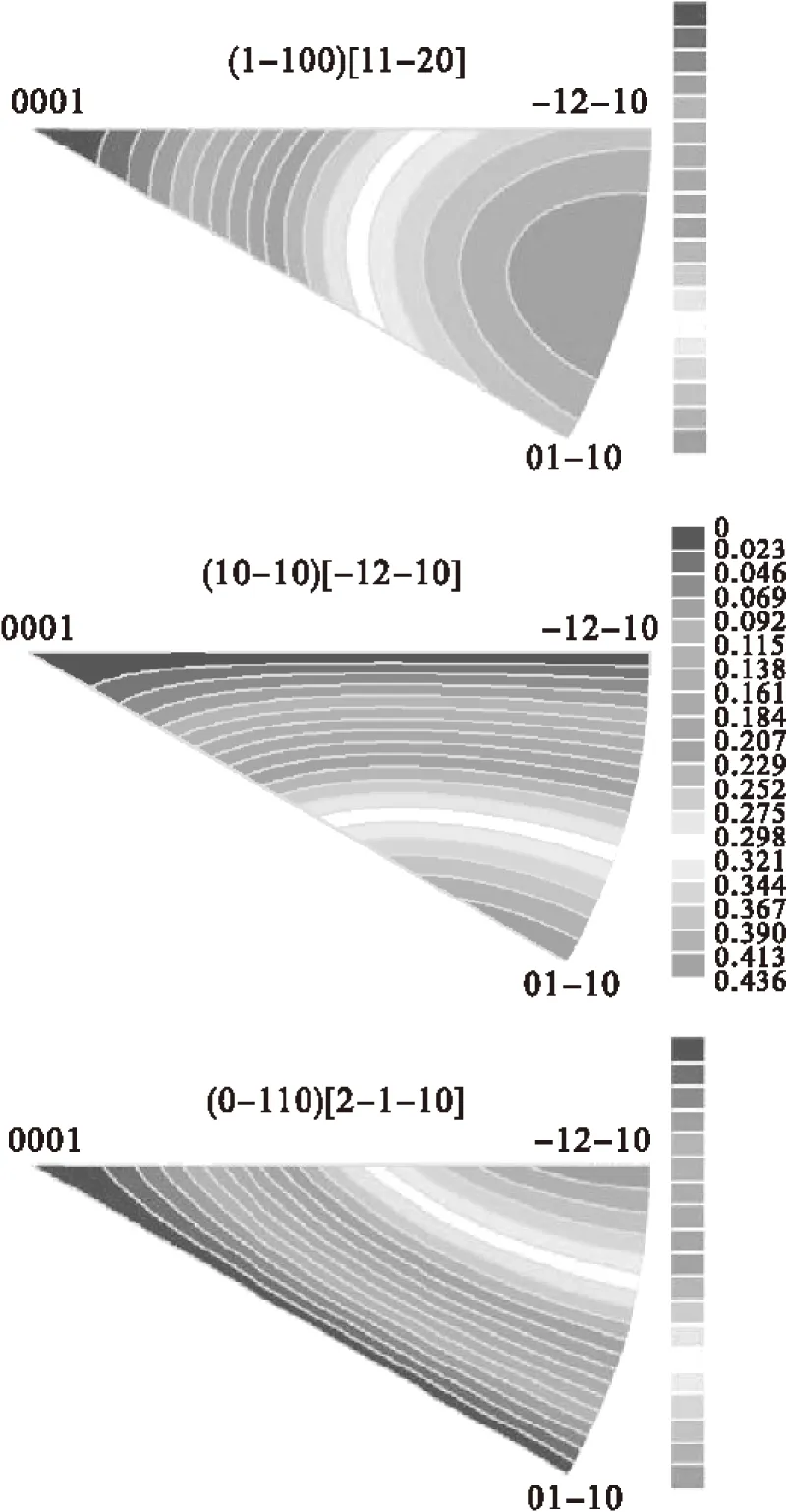
图5 柱面滑移系的Schmid因子分布图

从图中可以看出，基面滑移系、柱面滑移系和锥面滑移系都有最大0.5 的Schmid因子值，而锥面滑移系最大值仅为0.383，所以如果仅从Schmid因子来看，基面滑移系、柱面滑移系和锥面滑移系最易启动。但是，当Schmid因子值为0.5时，各个滑移系的θ和Ψ都不相同，对晶粒的取向要求不同。若Schmid因子值能取最大值，基面滑移系(图4)的最优取向在<0001>-<-12-10>取向线上，θ值为45°，且在很大的取向范围内都有较高的Schmid因子值；柱面滑移系(图5)的最优取向为θ=90°、Ψ=75°，且在很大的取向范围内都有较高的Schmid因子值；锥面滑移系(图6)的最优取向为为80°左右，Ψ为70°左右，但是Schmid因子普遍较低，最高Schmid因子值仅为0.383；锥面滑移系(图7)的最优取向在<0001>-<-12-10>取向线上，θ值为77.5°，和<0001>-<01-10>取向线上，值为12.5°，且在较大的取向范围内都有较高的Schmid因子值。

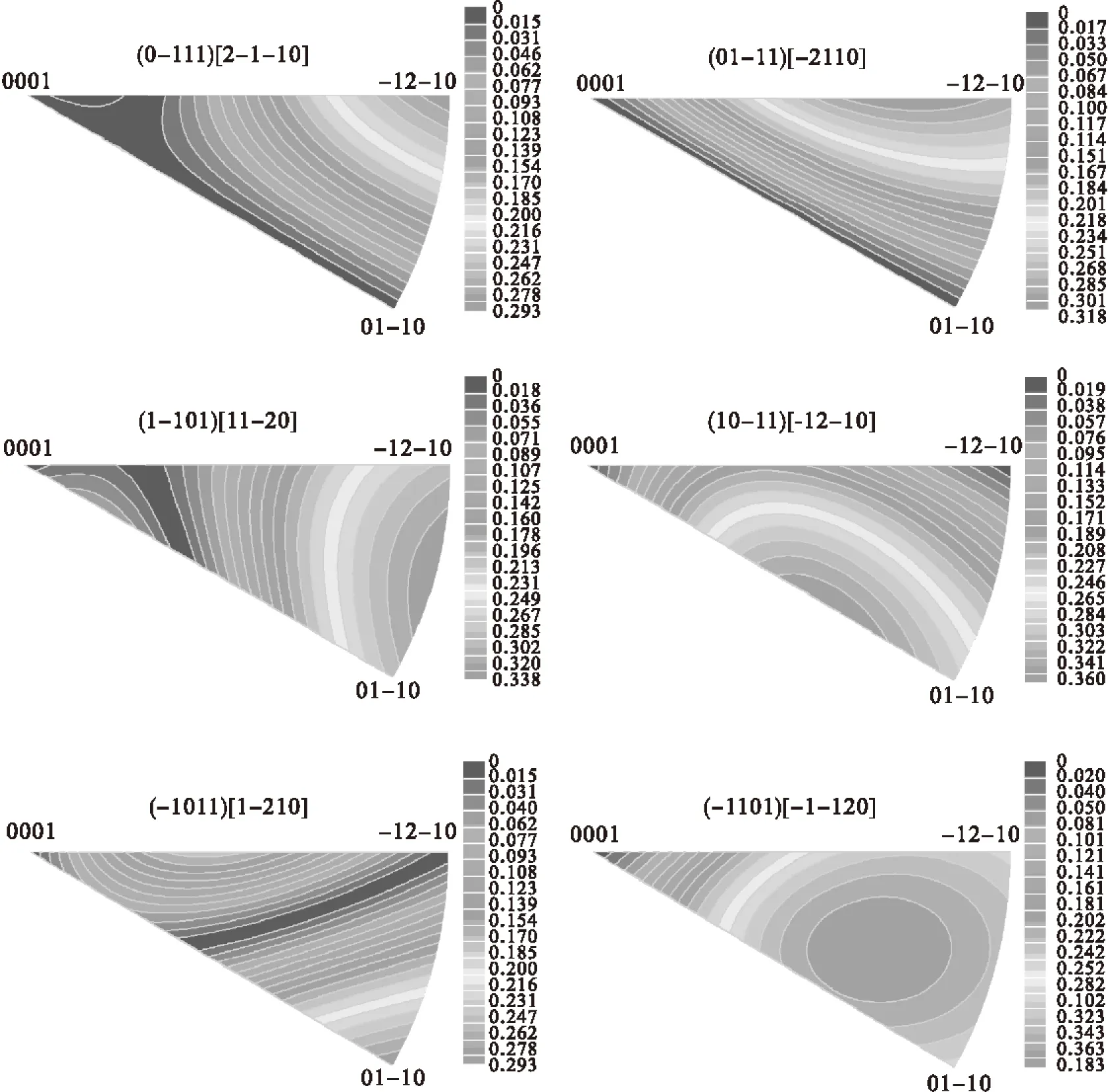
图6 锥面滑移系的Schmid因子分布图

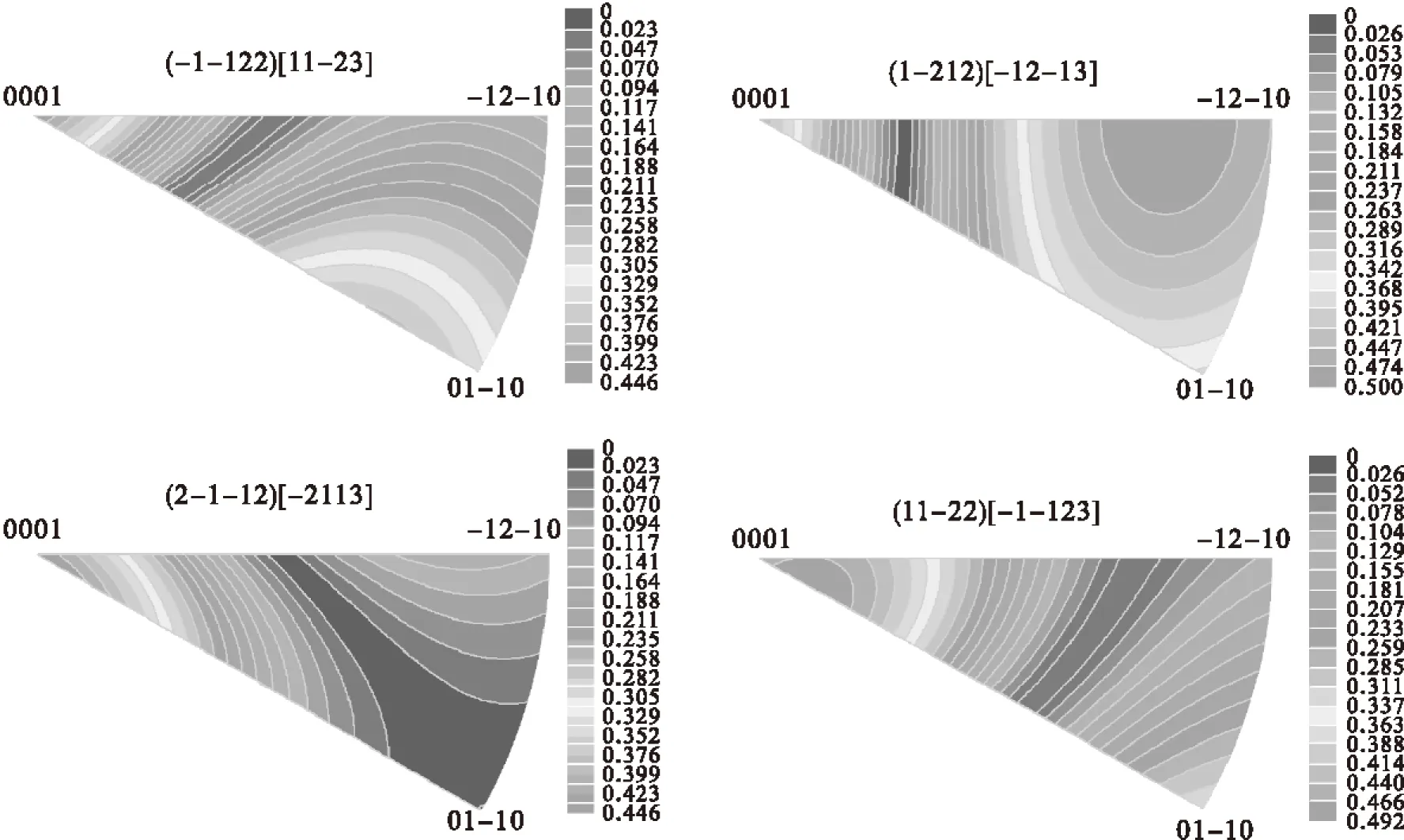
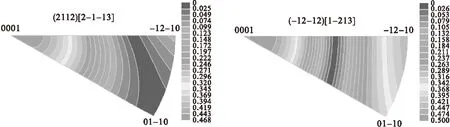
图7 锥面滑移系的Schmid因子分布图

此外，当晶体承受单向载荷作用时，除了位错滑移以外还有可能发生孪生。已有文献表明，当主要考虑Schmid因子对孪晶形成的影响时，晶粒发生压缩孪生变形对晶粒取向的要求相比拉伸孪晶形成的条件要严格得多，而拉伸孪生的发生对晶粒的取向要求则相对较为宽松。因此，在单向载荷过程中，如果单纯考虑Schmid因子对变形机制的影响，最易发生的有基面滑移、柱面滑移、拉伸孪晶和锥面滑移。但是判断镁合金的微观变形模式，除了考虑Schmid因子值的大小，应该同时考虑其他的一些影响要素，例如临界剪切应力、加载速度、晶粒尺寸、变形温度等。

3 结论

(1)通过对Schmid因子公式的推导，得到了镁合金位错滑移的Schmid因子在整个取向空间的计算公式。

(2)绘制了在整个取向空间的Schmid因子的分布图。基面滑移、柱面滑移和锥面滑移系的Schmid因子在取向空间中都有0.5的极大值；而锥面滑移系的Schmid因子普遍较低，当θ在80°左右，Ψ在70°左右时的最大值仅为0.383。

[1]Wang Y N,Chang C I,Lee C J.Texture and weak grain size dependence in friction stir processed Mg-Al-Zn alloy[J].Scripta Mater,2006,55(7):637-640.

[2]Wu L,Agnew S R,Brown D W,et al.Internal stress relaxation and load redistribution during the twinning-detwinning-dominated cyclic deformation of a wrought magnesium alloy,ZK60A[J].Acta Mater,2008,56(14):3699-3707.

[3]Barnett M R,Keshavarz Z,Beer A G.Influence of grain size on the compressive deformation of wrought Mg-3Al-1Zn[J].Acta Mater,2004,52(17):5093-5103.

[4]Clausen B,Tome′ C N,Brown D B.Reorientation and stress relaxation due to twinning:Modeling and experimental characterization for Mg[J].Acta Mater,2008,56(11):2456-2468.

[5]陈晓,傅高升,钱匡武,等.铸造镁合金的研究与发展现状[J].铸造技术,2004,25(11):855-858.

[6]Chapuis A,Driver J H.Temperature dependency of slip and twinning in plane strain compressed magnesium single crystals[J].Acta Mater,2011,59(5):1986-1994.

[7]Jiang L,Jonas J J,Luo A A.Evaluation of misorientation angle-axis set between variants during transformation of bcc to hcp phase obeying Burgers orientation relation[J].Scripta Mater,2006,55(9):771-774.

[8]Korla R,Chokshi A H.Strain-rate sensitivity and microstructural evolution in a Mg-Al-Zn alloy[J].Scripta Mater,2010,63(9):913-916.

[9]Koike J,Ohyama R.Geometrical criterion for the activation of prismatic slip in AZ61 Mg alloy sheets deformed at room temperature[J].Acta Mater,2005,53(7):1963-1972.

(责任编辑：吴萍 英文审校：刘敬钰)

CalculationofSchmidfactorsforslipsystemsinmagnesiumalloyunderuniaxialtensionandcompression

LOU Huan,WAN Gang,WU Bao-lin

School of Materials Science and Engineering,Shenyang Aerospace University,Shenyang 110136)

Aimed at magnesium alloys under uniaxial tension and compression conditions,the Schmid factor distribution of different slip systems(the basal slip,the prismatic slip,pyramidal and slips)in the whole orientation space is calculated.Results show that in the deformation process of magnesium alloys,the schmid factors for the basal slip,the prismatic slip and pyramidal slip all have a maximum value of 0.5 in the whole orientation space;while the Schmid factor for pyramidal slip is generally low,reaching the maximum value of only 0.383 whenθis approximately 80° andΨis 70°.The calculation provides a basis for analyzing the deformation mechanisms of magnesium alloys.

schmid factor;slip systems;magnesium alloy

2013-11-19

国家自然科学基金(项目编号：51371121)

娄欢(1989-)，男，江苏徐州人，在读硕士，主要研究方向：镁合金变形织构，E-mail:louhuanhuande@126.com；武保林(1963-)，辽宁鞍山人，教授，主要研究方向：高性能轻合金及其成型技术、金属形变与再结晶织构，E-mail：wubaolin@sau.edu.cn。

2095-1248(2014)01-0041-06

TG146.2+2

A

10.3969/j.issn.2095-1248.2014.01.010