相控阵雷达最优搜索策略的仿真算法研究

李其中

(华北科技学院，北京 东燕郊 101601)

1 引言

相控阵雷达是一种多功能、高性能的新型雷达系统，是现代高科技战争客观需要和科技技术水平发展到一定阶段的产物。正是因为相控阵雷达在军事方面的重要性，大国对相控阵雷达的研究日趋深入。目前，对于相控阵雷达的研究多采取仿真手段进行，根据使用手段不同，又可分为全实物物理仿真、半实物物理仿真和计算机数字仿真几种方法。全实物物理仿真使用物理存在的、实际的设备对雷达系统进行仿真，其突出的特点是逼真，是对雷达对抗设备进行评估实验有效的、往往也是最后的试验方式。全实物仿真完全使用实际设备，实验成本极为昂贵，针对性强但缺乏通用性，因此，在实际中往往受技术条件、物质条件以及环境条件等因素的限制。数字仿真是用一定的数学模型和各种数据来模拟试验环境和参试装备，用计算机软件控制试验过程，通过计算机演算得到试验结果。数字仿真具有经济、安全可靠、试验周期短、控制灵活、可重复性强等优点，是一种经济有效的仿真方法，因此得到了越来越广泛的应用。计算机仿真结果的可信度受到构建的数学模型及其它因素的影响。

本文根据相控阵雷达的基本原理，采用数字仿真的手段来探索相控阵雷达最优搜索策略，重点研究目标为建立相控阵雷达搜索的数学模型，实现在指定区域内单、多波束最优搜索策略的数学理论分析与仿真验证，提供基于指示信息的相控阵雷达波束单、多波束最优搜索策略数学仿真软件。

2 “遮挡”现象及单波束雷达扫描的数学模型建立与算法

2.1 “遮挡”现象数学模型

脉冲多普勒波形在单一重频的情况下存在距离遮挡问题，这主要由于脉冲多普勒体制雷达导引头采用同一个天线发射和接收，而发射和接收是时分引起的。

相控阵雷达系统是一个非常灵活复杂的系统，要模拟这样一个复杂系统的工作过程，面面俱到是不现实的，不可能做到和实际雷达设备一一对应。必须有所侧重，有所取舍，抓住影响其处理结果的关键因素和关心的主要方面，在保证一定的可信度的条件下，通过把各个模块的功能抽象化，融合后得到高效、可靠的仿真模型。

所以，根据上述雷达“遮挡”现象的基本原理，可以从建立简单的数学模型开始，一步一步建立起“遮挡”现象理想化的数学模型。

首先假设目标是可以被雷达探测到的，并设雷达到被探测目标的距离为D，雷达发射频率为f，光速为ls，雷达波的发射时间间隔为tlap。若考虑目标与雷达存在相对运动，可以将目标的运动速度离散化，假设目标在每个时间间隔tlap内匀速运动，且速度为V1、V2…Vi(目标向雷达方向相对运动，则Vi为正数，否则为负数)，第i束雷达波到达目标的时间为ti。设第i束雷达波返回的时刻为Ti，那么Ti=(i－1)× tlap+2ti;在雷达发射第i束雷达波时，存在:D=ls×ti+(V1×tlap+V2×tlap+… +Vi－1×tlap)+Vi×ti。从而可以得出:

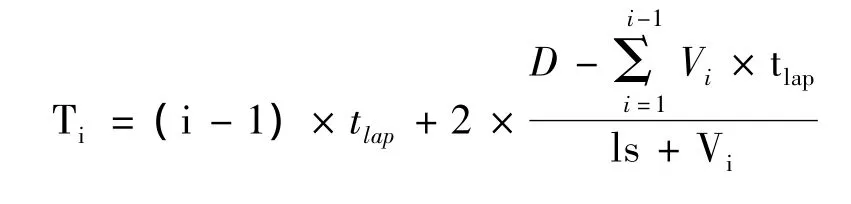
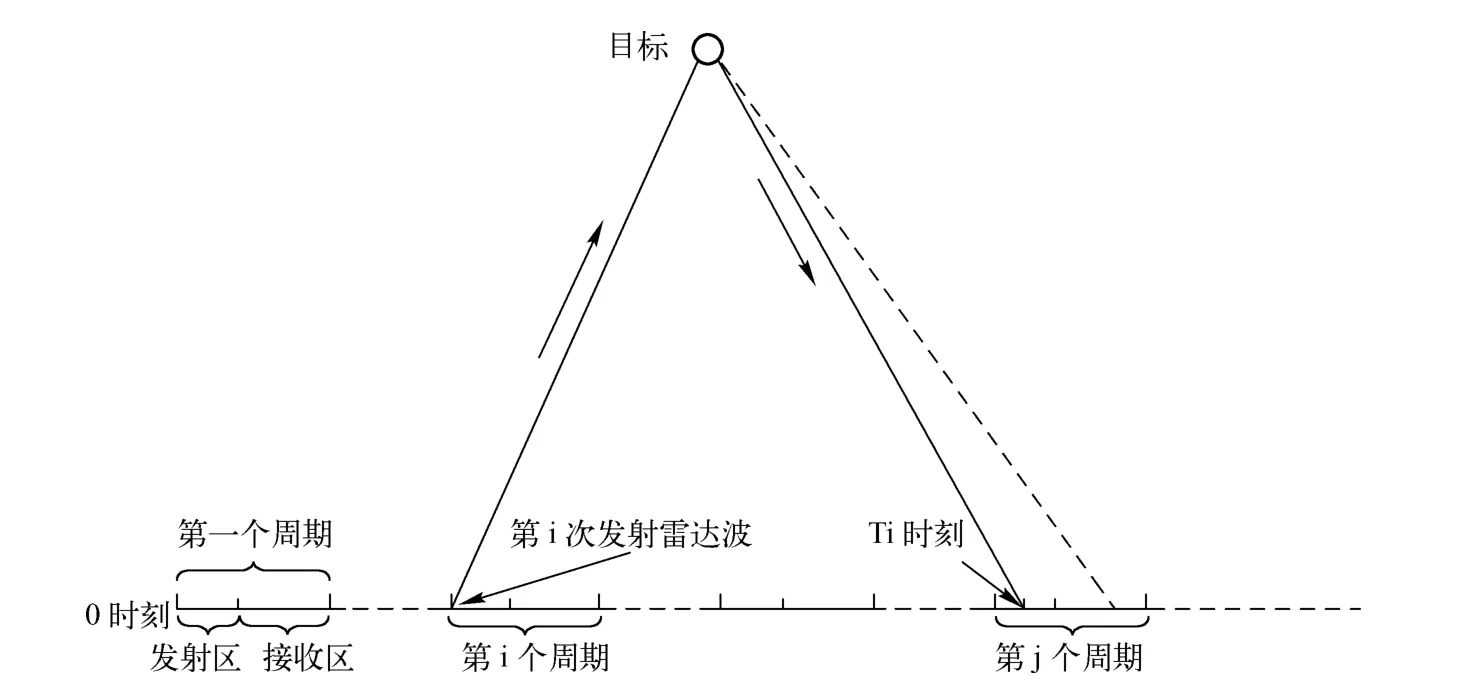
图1 雷达“遮挡”现象数学模型图

2.2 单波束雷达扫描算法

通过如图1“遮挡”数学模型，当第i个雷达波返回时的时刻Ti正好落在某个周期的发射区时，雷达是无法接收到该返回信号的，意味着信号丢失，此时雷达的“遮挡”现象就发生了。通过模型我们也可以计算出在雷达的一个扫描周期内能接收到的雷达返回波个数、丢失的雷达波个数，以及累计的返回波能量。具体算法的流程图如图2。

2.3 仿真模型建立的数据分析

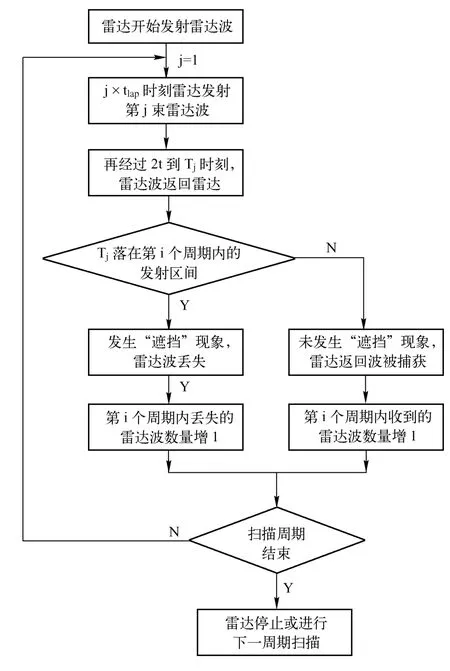
图2 雷达单波束搜索流程图

根据仿真程序计算，当占空比为0.4，在不同的频率下，接收的雷达返回波数随距离变化情况，从数据绘图中可以看出，当在频率为200 kHz、400 kHz、500 kHz、700 kHz时，返回波数量曲线存在明显的跳跃现象，也就是“遮挡”现象间断出现(参见图3);当频率为300、600 kHz时，雷达返回波数量曲线平缓、随着距离的增加逐步减少，通过进一步观察用程序计算生成的数据，发现此现象也发生于900、1200 kHz时。由此分析当雷达频率为光速整数倍数时，雷达返回波数量曲线平缓。同样，当设定雷达频率为300 kHz进行计算时，在不同的距离条件下，可以看出，当占空比达到一定数值时，接收的雷达返回波数回突变为0。当距离分别为 1、10、20、50、100、100 km 时，占空比都在0.49时接收的雷达返回波数突变为0，这也说明占空比在0.4左右为最优。此外，对于雷达返回能量的计算，也发现存在“遮挡”现象，并且随着距离的增加，能量是急剧减少的。这些与雷达在实际应用的情况是基本相符的。

3 多波束搜索仿真建模及算法

3.1 相控阵雷达搜索原理

相控阵雷达进行搜索时，按照事先设计的波位表工作。如何合理设计雷达的波位，在对空域进行完备搜索的前提下使雷达能量资源得到优化利用，成为雷达设计者需要考虑的问题。在雷达搜索数据率满足目标检测性能要求的前提下，波位安排紧凑固然可以不漏检任何空域，但会造成能量浪费，效率较低;波位安排疏松可以节省能量，但可能对某些目标漏检而不能进行完备搜索。此外，相控阵雷达进行波束扫描时，随着扫描角度的变化，存在波束展宽效应，使得其搜索性能下降，因此波位编排样式对相控阵雷达搜索性能的影响显著。

3.2 相控阵雷达波位排列方法

相控阵雷达波位排列方法有纵横排列、交错排列和交错纵横排列。图4给出了波束宽度为2.60情况下按照边界约束算法进行自动波位编排的结果，图中每个圆圈代表一个波位的中心位置，而且分别采用了以上三种波位编排样式。第一种方式扫描整个区域所需时间为23.647320 s，波位数目为645个，覆盖率为86.4%，重叠率0%。第二种方式扫描整个区域所需时间为40.904634 s，波位数目为783个，覆盖率为98.7%，重叠率0%。第三种方式。扫描整个区域所需时间为52.212401 s，波位数目为 920个，覆盖率为100%，重叠率3.56%。

可以看出，三种波位编排各有优点，纵列波位编排所需的波位数目最少，但是其覆盖率仅仅86.4%，当有限的相控阵资源是矛盾的主要方面时，或者目标分布密度小的区域可以考虑使用。交叠波位编排，虽然其覆盖率可以达到100%，虽没有遗漏但重叠率高，容易造成目标的冗余探测，限制了其应用范围，而交叠排列，并且覆盖率达到100，同时重叠率也较低，两种性能达到了较好的平衡，是一种常见的波位编排样式。总而言之，具体选择哪一种编排样式不能一概而论，应该针对实际背景和相控阵雷达系统资源的情况作出合理选择。

3.3 目标搜索仿真算法

根据上述相控阵雷达波位编排的理论及计算，采用上述三种波位的排列方式:纵横排列波位、交错波位和交错纵横波位(如图5所示)进行仿真(图中假设方位和俯仰的波束宽度相同)。

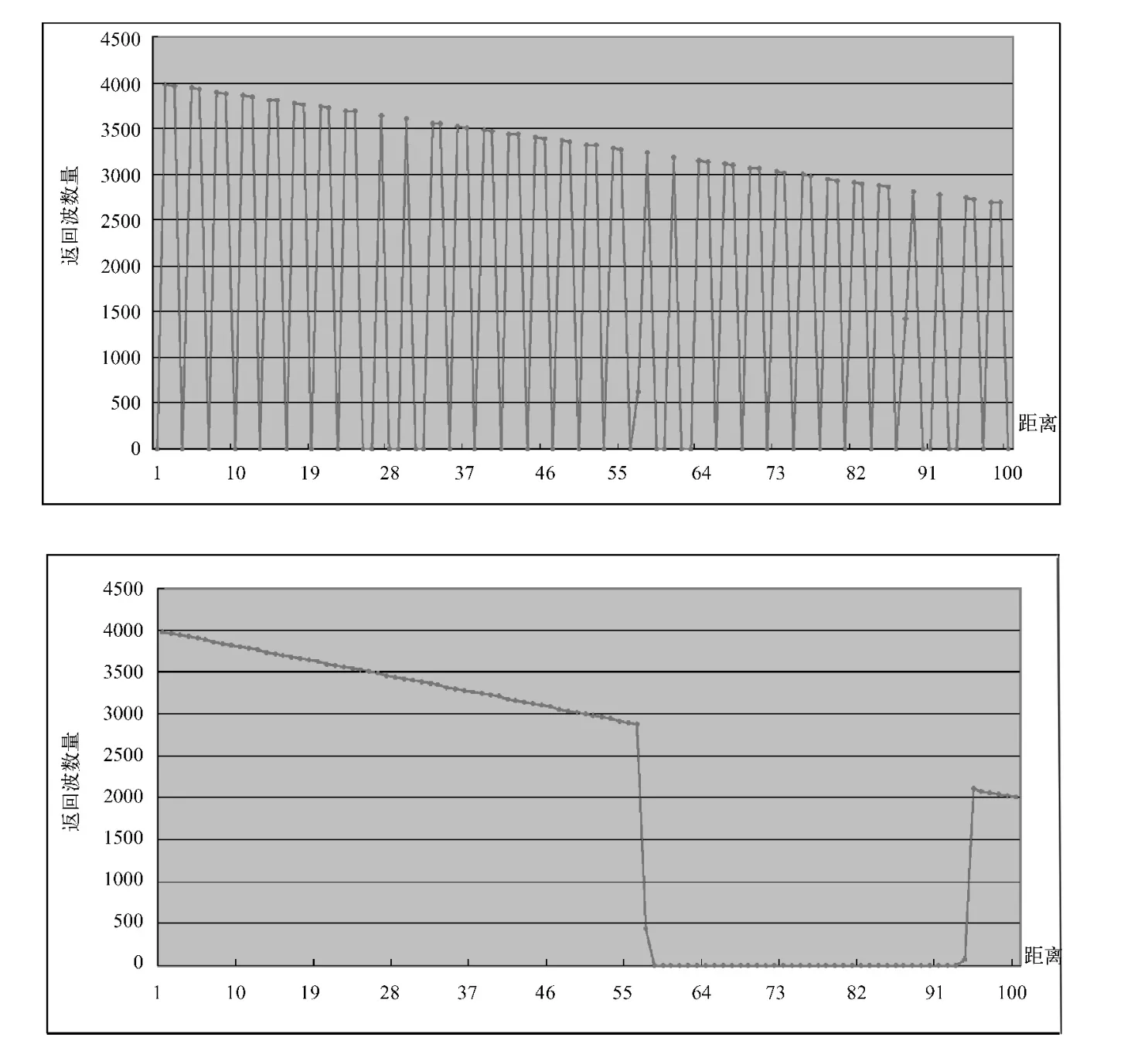
图3 频率为200 kHz(图左)、300 kHz(图右)时接收雷达返回波数随距离变化情况

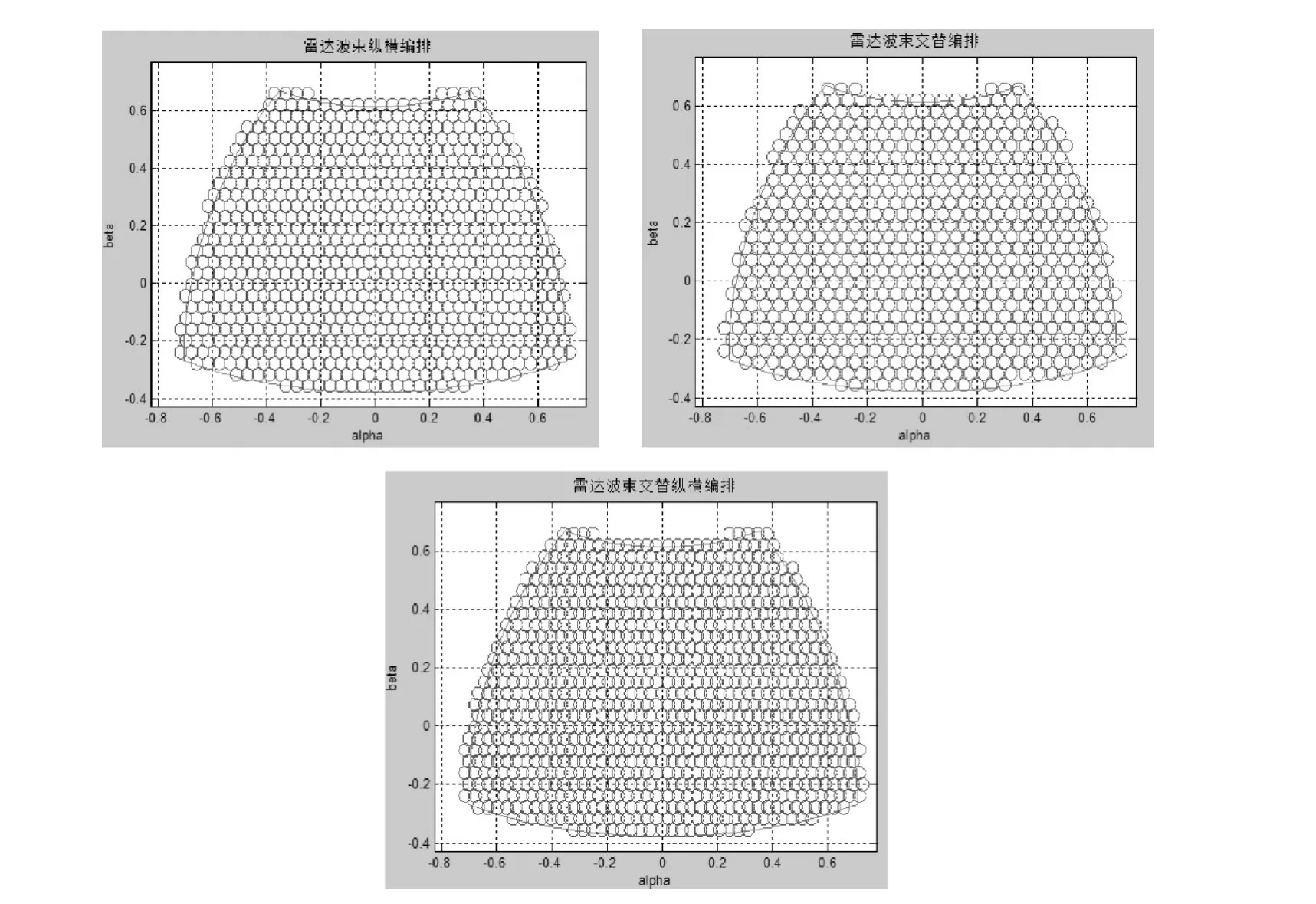
图4 三种不同的雷达波束编排效果图

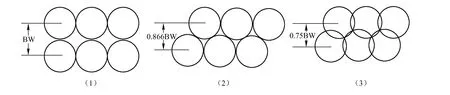
图5 波束的空间堆积方法

根据前述理论，假设按照第1种形式在给定空域内共计需要N个波束数目，则按照第2种形式需要1.15N个波束数目，按照第3种形式需要1.54N个波束数目。假设某雷达扫描区域A为［100，100］，［100，100］，雷达的波束宽度为 20，那么第一种形式在区域A内需要50个波束，按照第二种形式需要58个波束，按照第三种形式需要77个波束。

在前述单波束雷达扫描及“遮挡”现象的数学模型基础上，设第i束雷达波发射时，雷达距离目标的距离为Ri，则:Ri=ti×ls。设雷达的发射能量为E0，第i束雷达波的返回波能量为Ei，则:

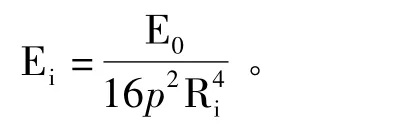
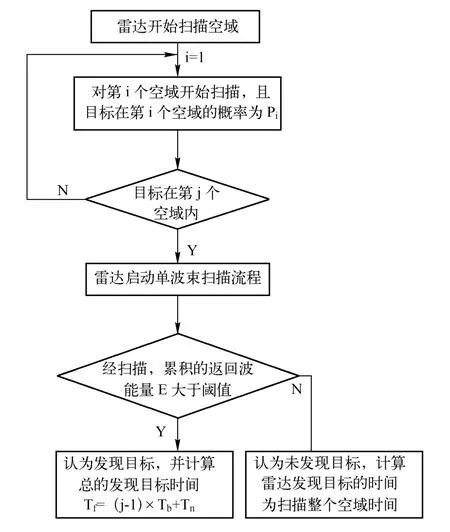
图6 雷达扫描空域流程图

当雷达波返回时刻落在第i个时间间隔的接收时间段，就会进行雷达返回波能量累积，就会累加Ei，只有当Ei达到能量阈值时，才被认为发现了目标。根据前述3种波位编排的波位排列方式和所需要的波位数目，设计一个具有3种不同的扫描方式的模型。假定目标一定在将要进行扫描的空域，对于能否发现目标，利用前面建立的雷达扫描的基本模型，根据目标的距离、雷达的频率、占空比、雷达接收返回波阈值等因素来判定。同时，假设目标出现在空域里某个波位的概率是不相等的。

以第一种波位编排方式为例，将从目标出现概率最大的波位开始编号1、2…n，并设概率分别为P1、P2…Pn(n为波位数)。根据这组概率设计了一个目标随机出现的算法，使得目标在第i波位的概率为Pi。设定雷达从概率最大的波位开始扫描，假如到发现目标为止，已经扫描了j个波位，从雷达启动扫描开始，发现目标的时间为Tf=(j－1)×Tb+Tn。其中Tb为雷达扫描一个波位所需的时间，Tn为在第j个波位里雷达发现目标所需的时间，流程如图6。

用以上方法可以针对每种波位编排方式进行仿真计算，对每种方式测试3组100次雷达发现目标的时间Tf，然后求得雷达发现目标的平均时间Ta，根据Ta就能分析出这3种波位编排方式中哪个发现目标的平均时间最短，就可以认为这种方式最优。当然这还要考虑到雷达频率、目标距离、占空比等因素，因此，需要在不同的雷达频率、目标距离、占空比条件下进行仿真计算，得出大量的数据进行分析，从而推导出最优的雷达搜索自适应算法，使雷达在目标距离改变的情况下，自动调整频率、占空比，以达到最短时间发现目标。

4 结论

本文重点针对雷达的基本工作原理、“遮挡”现象、单波束搜索、多波束搜索，分别建立其对应的数学模型，并根据所建立模型，在VC环境下开发相应的仿真程序(参见图7)，实现各模型的功能仿真。仿真程序能对单波束进行模拟计算，也可以对扫描空域时的多波束进行模拟计算。在仿真过程中，还对不同距离、频率、占空比下的“遮挡”现象和返回波能量情况进行了分析比较，计算了利用三种不同方式对某个空域进行搜索的发现目标平均时间。当然，在仿真过程中我们没有考虑环境噪声等因素，因此，在以后的工作中要进一步完善相控阵雷达在实际工作状态下的参数，以使得仿真过程更接近于真实情况，得到的数据更符合实际。

图7 雷达仿真模拟程序主界面

［1］ 超绍颖，杨文军.用于空间目标监视的相控阵雷达需求分析［J］. 现代雷达，2006，(01):16－19.

［2］ 李昊，于周秋.基于优先级的相控阵测量雷达调度设计［J］. 现代雷达，2006，(07):52 －55.

［3］ 周颖，王国玉，王雪松，肖顺平.基于启发式混合遗传算法的相控阵雷达最优化调度［J］.系统工程与电子技术，2006，(07):992 －996.

［4］ 李秋生.相控阵雷达导引头调度策略研究［J］.制导与引信，2006，(02):10 －14.

［5］ 卢建斌，胡卫东，郁文贤.基于Riccati方程的相控阵雷达稳态资源管理［J］. 现代雷达，2007，(06):1－5.

［6］ 袁振涛，宋锐，胡卫东，郁文贤.基于状态表调度的相控阵雷达高可用处理集群［J］.计算机工程与应用，2006，(09):183－185.

［7］ 周颖，王雪松，汪连栋，王国玉，谭旭东.基于遗传算法的相控阵雷达最优化调度研究［J］.系统工程与电子技术，2005，(12):1977 －1980.

［8］ Skolnik M I.Radar Handbook［K］.Second Edition.New York，USA:McGRAW －Hill Publishing Company(1990).

［9］ G Horne，T Meyer.Data farming:Discovering surprise［C］Proceedings of the 2004 winter simulation conference.Huntsville，AL，USA:Society for Computer Simulation International，2004，807－813.