带角度约束的倾斜转弯飞行器制导律设计
晁 涛,王松艳,杨 明
(哈尔滨工业大学 控制与仿真中心,哈尔滨 150080)
倾斜转弯(back-to-turn,BTT)飞行器不同于以往的侧滑转弯飞行器,只有一个主升力面,转弯时需要将升力面转到理想的方向,产生所需的机动加速度。针对这种飞行器设计制导律,需要结合其自身的运动特点,建立相应的制导律设计模型,综合考虑以特定角度攻击目标、合理分配过载要求等性能需求,因此,其制导律设计方法得到了广泛关注。
针对上述需求,文献[1]给出了具有角速率反馈形式的最优导引律,通过建立俯冲平面和转弯平面内的相对运动模型,引入落角约束要求,在能量最优的情况下达到期望的性能指标要求。而文献[2]给出了一种最优制导律,只使用角度反馈即可实现制导精度和落角约束的要求,适合应用于采用角跟踪伺服系统的雷达导引头。文献[3]利用拉格朗日法,构造带有落点和落角约束的飞行器运动方程,研究了制导系统中的动力学滞后对脱靶量和落角误差的影响。文献[4]应用SDRE方法将终端角度约束的制导律设计问题转化为非线性控制问题,并通过数值仿真验证了该制导律对控制回路动态有一定的鲁棒性。文献[5]基于比例导引律提出一种由末制导初始预定位置的几何关系获得导航系数的方位制导指令法,该方法能够满足期望的落角约束条件。文献[6-7]讨论了从制导模型中直接获得最优俯仰加速度指令和滚动角速度指令的方法,引入一种设计BTT飞行器制导律的思路。文献[8]在考虑BTT飞行器具有一阶加速度跟踪自动驾驶仪和零阶滚转角速率跟踪自动驾驶仪的情况下,利用拉格朗日乘子法对飞行器进行了最优制导律设计,得到理想的仿真结果。文献[9]通过对视线转率进行修整来获得调整参数,建立能够满足终端时间和落角要求的视线转率剖面,并应用二阶滑模控制方法跟踪期望视线转率剖面。文献[10]在视线测量存在延迟的情况下,基于改进的比例导引律,用开关控制函数代替视线转率设计滑模制导律,并应用闭环滤波法消除抖振。
通过对上述文献的分析可知,文献[1-5]考虑了落角约束的条件,没有考虑飞行器控制回路的动态特性;文献[6-8]考虑了飞行器控制回路的动态特性,但不能满足落角约束要求。目前鲜有针对BTT飞行器的考虑角度约束和控制回路动态特性的制导律设计方法。
本文针对BTT飞行器,在考虑控制回路动态特性的情况下,研究一种带角度约束的制导律设计方法。根据其控制方式,考虑控制回路的影响,建立以倾侧角和法向过载指令为控制量的设计模型。基于该模型,考虑终端角度约束条件,设计滑动模态变结构制导律,在满足落点精度要求的同时,满足终端角度约束条件。引入动态切换项以消除制导律开关函数项的抖振。最后,从理论推导和数值仿真两方面对本文的制导律与文献[1]中的最优制导律进行比较分析。
1 数学模型与问题描述
1.1 数学模型
目前已有的制导律设计模型多是以速度转率为控制量,当计算BTT飞行器的制导指令值时,需要进行转换,给实现带来不便。另外,以往制导律设计时,通常忽略控制回路动态特性对制导过程的影响,不利于提高制导性能[11]。因而,本文提出含控制回路动态特性、以倾侧角和法向过载指令为控制量的制导律设计模型。
为简化研究,将飞行器与目标间的三维运动分解为俯冲平面yoT和转弯平面zox内的二维运动来描述,如图1所示,图中oxsyszs为视线坐标系。由几何关系可知:
ηD=γD-λD
(1)
(2)
(3)
其中:v为飞行器速度;vD为速度在水平面内的投影;ρ为弹目相对距离;γD为vD与平面xoz间的夹角;ηD为vD与视线间的夹角;λD为俯冲平面内的视线高低角,即视线与平面xoz间的夹角。
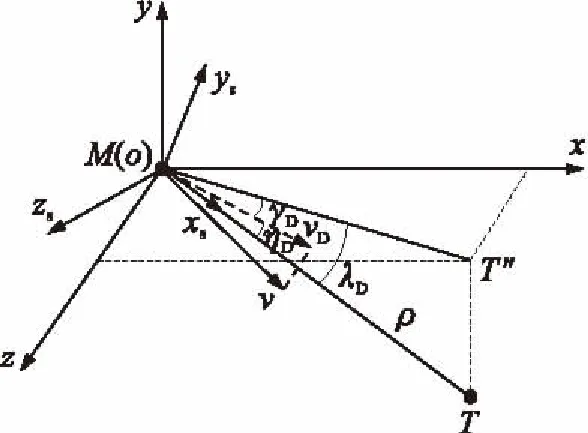
图1 俯冲平面内弹目相对运动示意图
将式(3)两边同时对时间t求导,整理得俯冲平面内的相对运动方程:
(4)
同理,令ηT=γT-λTT,得到转弯平面内的相对运动方程:
(5)
式中:vT为飞行器速度v在转弯平面内的投影,γT为vT与平面xoy间的夹角,ηT为vT与视线间的夹角,λTT为视线与平面xoy间的夹角。
(6)
假设飞行器有时间常数为τb的倾侧角自动驾驶仪和时间常数为τa的法向过载自动驾驶仪,即飞行器控制回路动态特性满足:
(7)
式中:nL,c,nL分别为飞行器的法向过载指令和实际法向过载;γv,c,γv分别为倾侧角指令和实际倾侧角。
(8)
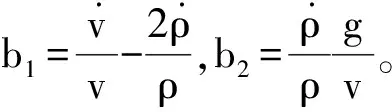
1.2 问题描述
考虑到以特定角度攻击目标的需求,可知飞行器的终端约束为
(9)
式中:tf为飞行结束时间,λD,f为期望落角。
综合上述制导律设计模型推导和约束条件,将制导律设计问题描述为:在考虑飞行器控制回路动态特性的情况下,针对式(8)所示的制导律设计模型,设计一种滑模变结构制导律,使飞行器满足式(9)。
2 滑模变结构制导律设计
本文采用滑模变结构方法,针对上节描述的制导律设计问题,给出如下定理。
定理1 针对式(8)所示的飞行器制导律设计模型,设计滑模变结构制导律:
(10)
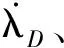
(11)

证明为满足俯冲平面内视线高低角的约束条件,将视线高低角期望动态表示为
(12)
进一步,将视线角转率的期望动态表示为
(13)
将式(13)带入式(6)中,可推导出倾侧角和法向过载的期望值γv,d和nL,d,即
(14)
式中:arctan2(·)表示反正切函数,且其角度取值范围为(-180°,180°]。
由式(12)~式(14)可知,要使视线角及视线角速率满足终端约束条件,可通过使倾侧角和法向过载达到期望值来实现,故选取滑模面的2个切换函数为
(15)
(16)
设计滑模面s1和s2的指数趋近律:
(17)
其中,趋近律系数k1>0,k2>0;切换项增益ε1,ε2为
(18)
式中:εi0>0;μ1>0,μ2>0,是切换项增益变化率的系数;δ1和δ2都是小正数,是自定义的边界参数,可根据实际需要选择。从式(18)可知,如果‖si‖>δi,趋近速度将增加,否则趋近速度会减小。与切换项增益εi取固定值相比,选用动态值时能够使系统以较小的速率趋近滑模面,起到消除抖振的效果。结合上述滑模趋近律可得:
(19)
(20)

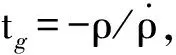
3 与最优制导律的比较
文献[1]给出的带落角约束的最优制导律为
(21)

(22)
式中各符号的定义同前。
首先,在飞行器末制导的开始阶段对2种制导律进行比较分析。末制导开始时,倾侧角γv和法向过载nL的初值为0,由式(7)和式(14)可得:
(23)
式中:
(24)

最优制导律的制导指令值如式(22)所示,法向过载指令与速度转率的平方相关,倾侧角指令的正切值与速度转率的比值相关,速度转率变化将引起指令值较大的变化,很容易造成指令值过大,因而在末制导初始阶段实际值很难跟踪上指令值。
其次,对飞行器在滑模变结构制导律的导引下进入滑模面运动后的情况与在最优制导律的导引下跟踪上制导指令值后的情况进行比较分析。
当系统处于滑模面运动状态时,s1=0,s2=0,则有
(25)
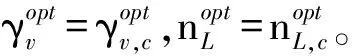
(26)
(27)
由式(26)和式(27)可知,当取k11=-1/tg,k21=-2/tg,k22=-1/tg时,系统在滑模面上实际的运动规律与最优制导律期望的飞行器运动规律相同,本文通过调整该制导律的系数,能够得到不同的制导效果。
4 数值仿真
分别将变结构制导律和最优制导律应用在BTT飞行器的末制导过程中进行仿真,其中初始条件设置如下:目标点距地面的高度为0;飞行器末制导起始位置距离目标点的距离为9.45 km,距地面高5 km,初始速度v0=300.0 m/s;初始弹道倾角为0°,弹道偏角为2°;终端约束条件要求落地时的弹道倾角为-90°;仿真结束的标志为飞行器的高度为0。根据收敛速度的需要确定制导律参数:k1=15/tg,k2=6/tg,k11=-1/tg,k21=-2/tg,k22=-1/tg。
仿真结果如图2和图3所示,其中SMC,optC分别表示变结构制导律指令和最优制导律指令。SM,opt分别表示经过姿态环节后的变结构制导律仿真结果和最优制导律结果。
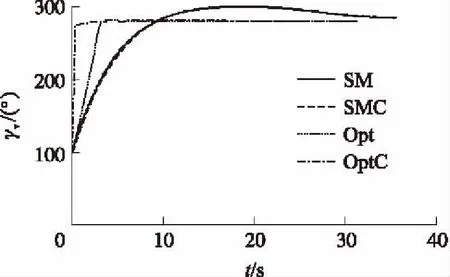
图2 倾侧角随时间的变化曲线

图3 法向过载随时间的变化曲线
从图2可见,最优制导律的初始段倾侧角指令很大,并要求瞬间达到,而实际上倾侧角在3.4 s之后才跟踪上指令。变结构制导律的倾侧角指令是从零开始缓慢增大,因而与实际倾侧角的变化几乎同步,跟踪性能好。从图3可见,在初始段,变结构制导律的法向过载指令从一个较小值开始缓慢增大;在末段时,指令下降到最小,此时飞行器控制能力的裕量较大,提高了攻击目标时抑制外界干扰的能力。从仿真结果可知,最优制导律的落点偏差为0.26 m,变结构制导律的落点偏差为0.15 m,二者落点位置几乎一致,均能达到位置要求。最优制导律的落角偏差为-0.42°,滑模变结构制导律的落角偏差为0.41°,均能满足落角要求。
5 结论
本文针对BTT飞行器的运动特点,考虑控制回路特性对制导过程的影响,建立了以倾侧角和法向过载指令为控制量的制导律设计模型。该模型与已有的设计模型相比,不需要进行指令转换,为BTT飞行器制导律设计模型的建立提供了一种新方法。
针对该制导律设计模型,提出了一种满足终端角度约束的滑模变结构制导律设计方法,通过合理的选择趋近律参数可以消除抖振,使系统更好地趋近滑模面。理论分析表明,在初始阶段该制导律较最优制导律对过载的需求小;通过调整参数,当系统进入滑模面运动后,飞行器能按最优制导律命中目标。该制导律在保证满足落点精度要求和落角约束条件的同时,在末制导过程中的各个阶段对过载的需求分配合理,终端速度损失小,因而具有较好的工程应用价值。
[1] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997:202-282.
ZHAO Han-yuan.Reentry vehicle dynamics and guidance[M].Changsha:National University of Defense Technology Press,1997:202-282.(in Chinese)
[2] 陈海东,余梦伦,董利强.具有终端角度约束的机动再入飞行器的最优制导律[J].航天控制,2002(1):6-11.
CHEN Hai-dong,YU Meng-lun,DONG Li-qiang.An optimal guidance law of maneuvering reentry vehicles with terminal angular constraint[J].Aerospace Control,2002(1):6-11.(in Chinese)
[3] 常超,林德福,祁载康,等.带落点和落角约束的最优末制导律研究[J].北京理工大学学报,2009,29(3):233-239.
CHANG Chao,LIN De-fu,QI Zai-kang,et al.Study on the optimal terminal guidance law with interception an impact angle[J].Journal of Beijing Institute of Technology,2009,29(3):233-239.(in Chinese)
[4] ASHWINI R,DEBASISH G.SDRE based guidance law for impact angle constrained trajectories[J].Journal of Guidance,Control,and Dynamics,2009,32(1):320-326.
[5] ASHWINI R,DEBASISH G.Satisfying terminal angular constraint using proportional navigation,AIAA-2009-6088[R].2009.
[6] STALLARD D V.Biased optimal guidance for bank-to-turn missile[C]//Proceedings of the American Control Conference.San Francisco:IEEE,1983:1 068-1 077.
[7] STALLARD D V.An approach to optimal guidance for a bank-to-turn missile[C]//Proceedings of the AIAA Guidance and Control Conference.New York:AIAA,1980:192-202.
[8] AGGARWAL R K,MOORE C R.Terminal guidance algorithm for ramjet-powered missiles[J].Journal of Guidance,Control,and Dynamics,1992,21(6):862-866.
[9] HARL N,BALAKRISHNAN S N.Impact time and angle guidance with sliding mode control[J].IEEE Transactions on Control Systems Technology,2012,20(6):1 436-1 449.
[10] LUM K Y,XU J X,KHALID A,et al.Sliding mode guidance law for delayed LOS rate measurement[C]//Proceedings of the AIAA Guidance,Navigation and Control Conference and Exhibit.Honolulu:AIAA,2008:1-11.
[11] TAL S,MOSH I,ODED M G.Sliding-mode control for integrated missile autopilot guidance[J].Journal of Guidance,Control,and Dynamics,2006,29(2):250-260.
[12] 王妍.可重复使用飞行器末段制导律设计方法研究[D].哈尔滨:哈尔滨工业大学,2010.
WANG Yan.Design method of terminal guidance law for reusable launch vehicle[D].Harbin:Harbin Institute of Technology,2010.(in Chinese)

