桥梁用三角形钢板阻尼器恢复力模型的参数确定

刘腾飞 沈 星 叶爱君

1 引 言

金属阻尼器具有构造简单、滞回耗能能力好、形式多样、坚实耐用、经济性好等优点，是国内外广泛研究的一种结构耗能减震装置[1,2]。在各种金属阻尼器中，X形和三角形软钢阻尼器具有沿高度范围内各截面等厚度处同时屈服的优点，因而很多学者对其进行了大量的研究，并在建筑工程中得到了一定应用[3,4]。

然而，三角形钢板阻尼器在桥梁抗震中的研究和应用还较少。同济大学沈星、叶爱君等(专利公开号：CN102953327A)以三角形钢板为基本构件，提出了新型的桥梁横向钢阻尼器，使得三角形钢板阻尼器可以很方便地应用于桥梁减震。在桥梁减隔震体系中，三角形钢板阻尼器通常与活动支座组合使用，对阻尼器本身的强度和位移能力有较高的要求，但设置空间有限。因此，在桥梁减震优化设计中，必须要能较准确而且方便地确定钢阻尼器的力学参数。

三角形钢板阻尼器一般采用双线性恢复力模型[5]模拟其弹塑性性能，关键的力学参数包括屈服前刚度、等效屈服力、屈服后刚度和设计变形能力，而这些参数均要在得到钢板从弹性到塑性破坏全过程的力-位移曲线后才能确定，而且钢板进入塑性阶段后，应力重分布非常复杂，应变分布的均匀性也不符合理想状态，其变形随三角形板尺寸的变化规律也与弹性状态有所不同。基于这些原因，应用弹塑性力学的基本理论推导就难以满足桥梁减震设计的需求，而需要采用较为精确的板壳有限元方法来计算，这对于实际工程应用来说过于复杂了。

为了给桥梁工程界提供一个实用的简化估算钢阻尼器弹塑性力学参数的方法，本文结合了弹塑性理论推导和有限元模拟分析的各自优势展开研究。首先从三角形钢板阻尼器的工作原理出发，推导钢板首次屈服力和首次屈服刚度的理论公式，然后，针对桥梁工程中可能的选型尺寸，基于ABAQUS有限元软件，建立大量钢板三维板壳模型，得到钢板的双线性恢复力模型曲线，重点研究了钢板几何尺寸对于钢板的恢复力模型力学参数(屈服后刚度、等效屈服力和位移能力)的影响，并用线性统计回归法处理各参数的数据，建立近似计算公式。最后对比有限元值和公式值，验证近似计算公式的正确性。

2 三角形钢板首次屈服力、首次屈服刚度理论公式

三角形钢板的底边宽度为B，高度为H，钢板厚度为t，三角形钢板顶点处受到的水平力为F，离三角形钢板顶点x处截面边缘的应力为

(1)

可见，三角形钢板沿高度范围内各截面最外缘点的应力相同。当钢板首次屈服时，σ恰好达到屈服应力σy，根据弹性力学理论，临界地震水平力即钢板首次屈服力

(2)

此时，对应的三角形钢板的屈服曲率

(3)

对屈服曲率进行两次积分得到顶点的水平位移

(4)

根据式(2)和式(4)可以得到三角形钢板各截面的首次屈服刚度

(5)

3 三角形钢板恢复力模型参数确定方法

除钢板的首次屈服刚度外，三角形钢板阻尼器的其他力学参数采用较为精确的有限元模拟计算结果来回归计算公式，为此建立了大量不同几何尺寸的钢板模型进行弹塑性有限元破坏分析，并得到了不同尺寸三角形钢板的力—位移关系图，进而得到各模型的主要力学参数值，最后对所得数据进行统计回归，得到了各参数的近似计算公式。

3.1 三角形钢板弹塑性性能有限元分析

3.1.1有限元计算模型

三角形钢板的尺寸如图1所示。材料为Q345钢材，应力—应变关系偏保守地采用理想弹塑性模型，如图2所示。主要参数如下：弹性模量E=2.05×105MPa，泊松比ν=0.3，屈服应力σy=345 MPa，屈服应变εy=0.001 683。而钢材极限应变εu的取值则与钢阻尼器的最大位移能力直接相关。《低合金高强度结构钢》[6]规定厚度6 cm以下的Q345钢材的断后伸长率在20%以上，即Q345钢材的断裂应变大于0.20。但在地震这种往复荷载作用下，钢材的极限应变取值要有所折减。文献[7]给出了AASHTO规范中grade 40(屈服应力300 MPa)，钢筋的有效极限应变为0.122左右，而钢材断裂应变为0.20，屈服应变约为0.03。本文中，Q345钢材的极限应变εu偏保守地取为屈服应变的40倍，即εu=0.067 32。

图1 模型尺寸示意图Fig.1 Diagrammatic sketch of model dimensions

图2 钢材本构曲线Fig.2 Steel constitutive curve

单块三角形钢板的三维实体有限元模型(壳单元)如图3所示，在有限元分析中利用短时间内的顶点位移模拟地震作用，三角形钢板底端固定，顶端自由。模拟分析完成后，提取时间历程内节点1处水平力和水平位移，提取节点2处Mises等效应力和最大主应变。

3.1.2均匀性分析

理论上，三角形钢板阻尼器的特点是：地震作用下，沿钢板高度范围内，钢板各截面同时屈服耗能，能够充分利用钢板的塑性变形能力，以实现最佳抗震效果。

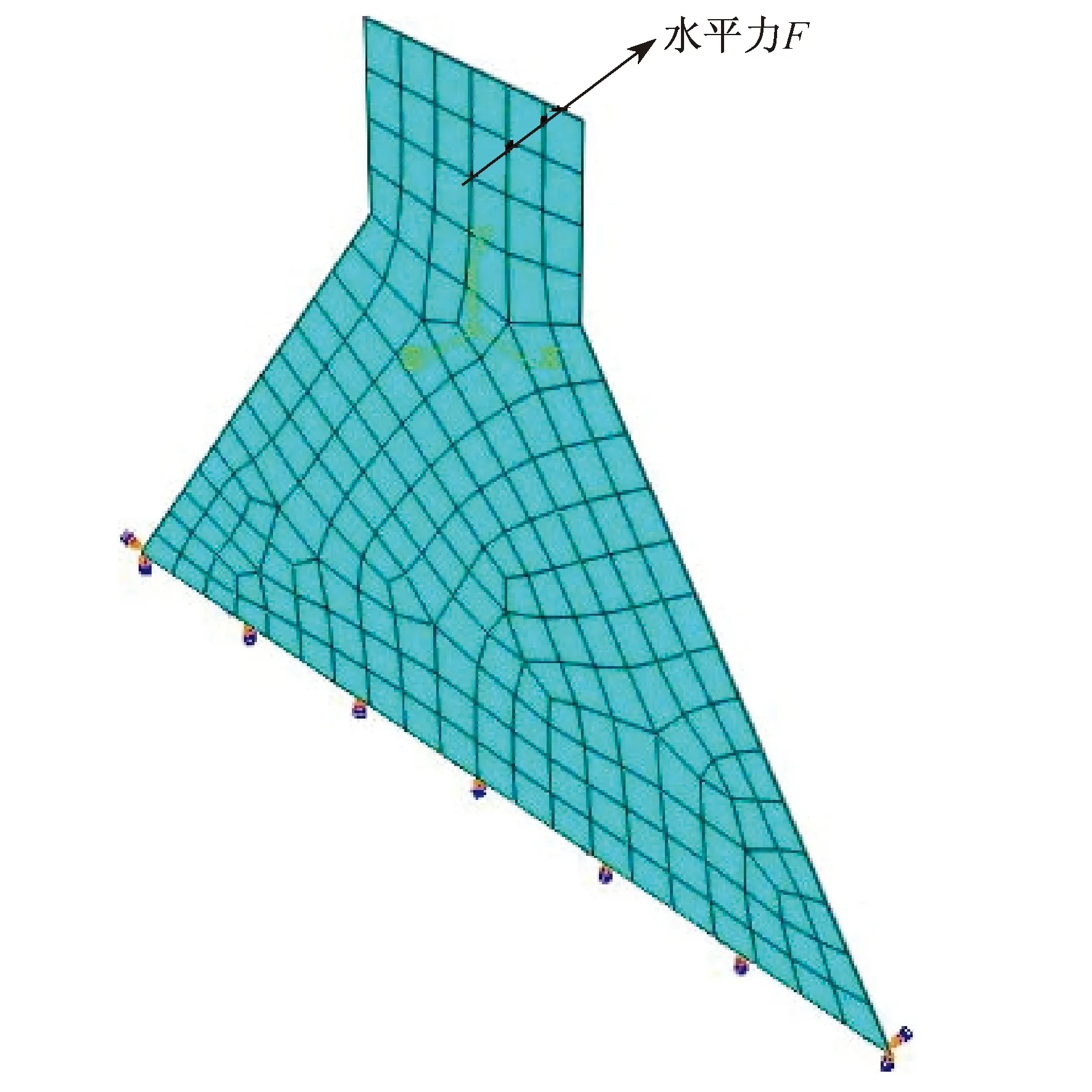
图3 边界条件与网格划分Fig.3 Boundary condition and mesh generation

但实际上，三角形钢板的弹塑性性能并不能达到这么理想的效果。图4所示分别为2个代表性几何尺寸的模型在首次屈服时的应力分布情况。图5所示分别为2个代表性几何尺寸的模型在钢板破坏时的最大主应变分布情况。

图4 钢板首次屈服时Mises应力分布图Fig.4 Mises stress distribution at steel plate first time yielding

通过对比分析，可以发现：在有限元分析中，首次屈服时不同尺寸模型的Mises应力分布均匀性有很大差异，且与模型的宽高比B/H有关：B/H越大，应力均匀性越差。这种情况与理论设想的“全截面屈服”有所不同。当B/H在一定范围时，可以保证大部分截面同时屈服，但是最后破坏时截面应变的同步性很差。此外，钢板达到位移能力时，不同模型的钢板最大主应变分布状况相差不大，应变最大值均出现在节点2附近区域，与理论分析设想一致。但应变分布均匀性在B/H接近1时，比B/H取其他值时有明显改善。

从上述现象分析中，可以得出如下结论：三角形钢板在大位移作用下，为获得良好的钢板屈服耗能效果，应控制宽高比B/H在合理范围内。通过对大量钢板模型的屈服时应力图和破坏时应变图分析，得到宽高比B/H的合理范围为0.67～1.50。如果采用等强度梁理论进行阻尼器初步设计，由于各截面应力、应变的不均匀性，会产生很大的计算误差，无法满足工程需要。因而采用基于有限元方法计算阻尼器恢复力模型各力学参数是必要的。

3.1.3力—位移关系曲线

图6所示为2个代表性几何尺寸的三角形钢板阻尼器模型的力—位移关系曲线。从图6中可知：三角形钢板阻尼器的力—位移曲线呈现明显的“双线性”，且有限元分析结果与基于等能量原理的双线性模拟曲线具有很好的吻合效果。利用力—位移关系曲线，三角形钢板恢复力模型的关键力学参数也可以容易地得到，为进一步研究几何尺寸对阻尼器恢复力参数的影响提供了方便。

Ky—首次屈服刚度；Kh—屈服后刚度；Feff—等效屈服力；Du—极限位移图6 三角形钢板阻尼器的力—位移曲线Fig.6 Force-displacement curve of the steel triangular plate damper

3.2 阻尼器恢复力模型参数的近似计算公式

在建立三角型钢板有限元模型时，根据桥梁墩顶的构造特点，选取了可能的金属阻尼器尺寸：板宽B分别取0.4 m、0.5 m、0.6 m、 0.7 m、0.8 m、0.9 m、1.0 m；板高H分别取0.3 m、0.4 m、0.5 m、0.6 m；板厚t分别取0.01 m、0.02 m、0.03 m。根据不同尺寸的取值组合，共建立84个模型，得到各模型恢复力曲线，研究几何尺寸对各力学参数的影响，并用线性统计回归法得到各参数的近似计算公式，以便用于桥梁减震设计。

3.2.1钢板的位移能力

在桥梁抗震设计中，横向金属阻尼器需要具有足够的变形能力以适应抗震的需要。本文偏安全地认为三角形钢板在地震力作用下，横截面最外缘点最大主应变达到40倍屈服应变时，顶点水平位移达到极限值，此时节点1极限水平位移即为钢板的位移能力。图7给出了位移能力有限元分析值与钢板尺寸的关系曲线。从图7可以发现：

(1) 板高对位移能力影响显著，板高增大，位移能力迅速提高，位移能力随板高线性增长；

(2) 板宽对位移能力影响为板宽增大，位移能力缓慢变化(有升有降)；

(3) 板厚对位移能力影响为板厚增大，位移能力减小。

图7 位移能力与钢板尺寸关系曲线Fig.7 Relation between the displacement and steel plate dimension

统计所有尺寸钢板的位移能力有限元分析值，并采用线性回归法拟合，得到在建议宽高比范围内(0.67～1.5)三角形钢板位移能力Du近似计算公式为

t=0.01 m，

Du=-106BH+90B+843H-101

(6a)

t=0.02 m，

Du=163BH-90B+387H+23

(6b)

t=0.03 m，

Du=-197BH+44B+545H-57

(6c)

式中，Du单位为mm；B，H单位为m。

3.2.2钢板的屈服后刚度

《城市桥梁抗震设计规范》(CJJ 166—2011)中条文说明9.24提出：地震作用下，为控制减隔震装置发生过大的位移，除要求提供减隔震装置阻尼外，同时要求减隔震装置具有一定的屈服后刚度，提供自恢复力。因而三角形钢板阻尼器应具有足够的屈服后刚度。图8给出了钢板屈服后刚度有限元分析值与钢板尺寸的关系曲线。从图8可以看出：

(1) 板高对钢板屈服后刚度的影响显著：板高越大，屈服后刚度迅速越小，屈服后刚度与板高平方近似成反比。

(2) 板宽对钢板屈服后刚度的影响：板宽越大，屈服后刚度越大，屈服后刚度随板宽增大，近似呈线性增长。

(3) 板厚对钢板屈服后刚度的影响：板厚增加，屈服后刚度迅速提高，屈服后刚度与板厚平方近似成正比。

图8 屈服后刚度与钢板尺寸关系曲线Fig.8 Relation between the post yield stiffness and steel plate dimension

统计有限元分析中所有尺寸钢板的屈服后刚度，并采用线性回归法拟合数据，得到在建议宽高比范围内(0.67～1.5)，钢板的屈服后刚度近似计算公式：

(7)

式中，B，H，t单位为m。

3.2.3钢板的等效屈服力

在利用三角形钢板阻尼器进行桥梁抗震设计时，钢板的等效屈服力是很重要的设计参数。其余条件确定时，等效屈服力越小，钢阻尼器耗能越早，对桥梁上部结构的保护作用越强,但为满足桥梁正常使用状态约束的需求，金属阻尼器的等效屈服力也不宜太小，一般可控制在固定支座吨位的10%左右。图9给出了三角形钢板等效屈服力的有限元分析值与钢板几何尺寸的关系曲线。从图9可得以下规律：

(1) 板高对等效屈服力影响为：板高增大，等效屈服力迅速减小，等效屈服力与板高近似成反比。

(2) 板宽对等效屈服力影响显著，板宽越大，等效屈服力越大，等效屈服力与板宽近似成正比关系。

(3) 板厚对等效屈服力影响显著，板厚增大，等效屈服力迅速增大，等效屈服力与板厚的平方近似成正比。

图9 等效屈服力与钢板尺寸关系图Fig.9 Relation between the equivalent yield force and steel plate dimension

根据等效屈服力随钢板尺寸的变化规律，本文对式(4)进行修正得到等效屈服力Feff在建议宽高比范围内(0.67～1.5)的近似计算公式，其中γ=1.3是采用线性回归法对等效屈服力有限元分析数据拟合得到的。

(8)

3.3 各参数近似计算公式的正确性验证

钢板阻尼器恢复力模型参数的近似计算式(6)、式(7)、式(8)都是应用线性回归法对有限元数据分析得出的。线性回归法对于数据的良好性有较高要求，而且有参数不稳定的缺点。为满足工程中的应用，必须对近似计算式(6)、式(7)、式(8)进行验证，保证近似计算的稳定性和可靠性。

(1) 图10的计算结果表明：在建议宽高比范围内(0.67～1.5)，利用式(6)得到的位移能力值与有限元数据相比，除个别数据点外，误差均在-5%～5%之间。式(6)可以很好地吻合位移能力的有限元数据。

(2) 图11计算结果表明：在建议宽高比范围内(0.67～1.5)，式(7)与有限元分析数据可以很好地吻合：除个别数据点外，公式值与有限元分析值误差均在-12%～12%之间。

(3) 图12计算结果表明：在建议宽高比范围内(0.67～1.5)，式(8)与有限元分析数据可以很好地吻合：除去个别数据点外，公式值与有限元分析值误差均在-10%～10%之间。

4 结 论

本文针对三角形钢板阻尼器的优化设计中恢复力模型力学参数的确定问题，首先基于弹性力学理论，推导了钢板首次屈服刚度理论公式。然后采用有限元方法，建立大量不同尺寸钢板模型进行钢板破坏的弹塑性分析，得到各模型力—位移曲线，并用线性回归方法确定了各力学参数的近似计算公式，最后对公式的正确性进行验证。本文主要结论如下：

图10 位移能力公式值与有限元值误差Fig.10 Displacement capacity comparison between empirical formula and FEM analysis

图11 屈服后刚度公式值与有限元值误差Fig.11 Post yield stiffness comparison betweenempirical formula and FEM analysis

图12 等效屈服力公式值与有限元值误差Fig.12 Equivalent yield force comparison between empirical formula and FEM analysis

(1) 钢板的应力均匀性与宽高比B/H有关。B/H越大，应力均匀性越差。为较好发挥钢材屈服耗能能力，建议三角形钢板宽高比B/H限制在0.67～1.5。

(2) 有限元分析结果表明，尺寸的变化对于三角形钢板阻尼器各参数的影响非常显著。

(3) 本文中给出的首次屈服刚度理论公式以及其他各力学参数近似计算公式，很好地反映了不同参数随钢板尺寸变化的规律。与有限元计算结果对比表明，各公式可以满足工程中的精度要求。

[ 1 ] Kelly J M, Shinner R I, Heine A J. Mechanisms of energy absorption in special devices for use in earthquake resistant structures [J]. Bulletin of New Zealand National Society for Earthquake Engineering, 1972, 5(3): 63-87.

[ 2 ] Skinney R I, Kelly J M, Heine A J, et al. Hysteresis dampers for the protection of structures from earthquakes [J]. Bulletin of New Zealand National Society for Earthquake Engineering, 1980, 13(1): 22-26.

[ 3 ] Whittaker A S, Bertero V V, Thompson C I, et al. Seismic testing of steel plate energy dissipation devices [J]. Earthquake Spectra, 1991,7(4):563-604.

[ 4 ] Tsai K C, Chen H W, Hong C P, Su Y F. Design of steel triangular plate energy absorbers for seismic resistant construction [J]. Earthquake Spectra, 1993,19(3):505-528.

[ 5 ] 叶爱君，管仲国. 桥梁抗震[M].2版.北京：人民交通出版社，2011:126-127.

Ye Aijun, Guan Zhongguo. Seismic design of bridges[M]. 2nd Edition. Beijing: China Communications, 2011:126-127. (in Chinese)

[ 6 ] 国家质量监督检验检疫总局.GB/T 1591—2008低合金高强度结构钢[S].北京：中国标准出版社，2011.

General Adminstration of Quatity Supervision, Inspection and Quarantine of the People′s Republic of China. GB/T 1591—2008 High strength low alloy structural steels [S]. Beijing: China Standards Press, 2011. (in Chinese)

[ 7 ] Priestely M J N, Seible F, Calvi G M. Seismic design and retrofit of bridges [M]. New York: John Wiley and Sons, Inc, 1996.