基于压缩感知的自适应数据融合算法
李 莉,刘晓乐
(河南工程学院 计算机学院,河南 郑州451191)
压缩感知(Compressive Sensing,以下简称CS)是由Donoho和Candes等[1]在2006年提出的一种数据获取理论.2006年,Haupt和Nowak[2]将压缩感知理论应用到多个信号的环境中,但他们的方法仅研究了多个信号的互相关性,却没有考虑单个信号的内相关性.Baron等[3]在压缩感知理论的基础上提出了分布式压缩感知(Distributed Compressed Sensing,以下简称DCS).
本研究提出了一种基于分布式压缩感知的自适应数据融合路由算法,对各节点进行数据融合时进行自适应调整,在路由过程中收集、融合相关节点的感知数据以减少总的传输和融合能量开销.
1 基于分布式压缩感知的数据融合
1.1 压缩感知理论
CS理论指出,只要信号是可压缩的或在某一个正交空间具有稀疏性,那么就可以用一个比较低的频率(M≪N)进行信号采样,然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号.
假设X为长度为N原始离散信号,X在时域空间RN的矢量元素为X n(n=1,2,…,N),Ψ域的一组标准正交集为{φ1,φ2,…,φn},则信号X可以由{φ1,φ2,…,φn}线性表示为

其中,X和Ψ是同一信号在不同域的等价表示,如果X只是K(K≪N)个基向量的线性组合.
1.2 分布式压缩感知算法
分布式压缩感知技术考虑多维信号集合的时空相关性,假设多维信号集合具有联合稀疏性,感知节点根据联合稀疏性进行基于CS的编码并将压缩后的观测传送给Sink,Sink对压缩后的全体观测进行联合解码[4].
假设一组可压缩的多维信号集合xl,…,xj在矩阵Ψ上具有共同的稀疏分量和稀疏信息[5],则信号xl的稀疏系数向量θl=(θl(1),…,θl(m))T可分解为θl=θc+~θl,l∈{1,2,…,J},则xc=Ψθc,‖θc‖0=kc;^xl=Ψ^θl,‖^θl‖0=kl(kl<kc);xl=xc+^xl.其中,kc和kl分别是稀疏向量θc和θl的非零个数.
为了充分利用多维信号集合的分布式特点,假设Sink事先给感兴趣区域的每个节点发送一个相同的种子Seed,每个节点根据收到的种子产生相同的伪随机矩阵(Φ=Φi=…=Φj).那么,当获得足够多的观测时,多维信号集合的联合重构可以通过求解li最优化来解决.
1.3 分布式压缩感知的网络传输能耗
假设节点Sl(l∈{l,…,J})将可压缩信号xl(l∈{l,…,J})投影到基矩阵Ψ上,得到稀疏系数向量θl(l∈{l,…,J}).因为各个节点独立编码,无法获得多维信号集合的联合稀疏结构,所以节点无法确定精确联合重构多维信号集合所需向Sink传输的最少观测个数[6],只能根据自身稀疏系数向量θl中非零个数nl向Sink传输nl=t(kc+kl)个观测,则整个网络能耗为

2 基于压缩感知的自适应数据融合
2.1 算法分析
在WSN中各节点只携带共同观测的信息yc沿着路由在当地节点进行数据融合,即当信息迁移到节点Sl(l∈{2,…,J})时,通过比较θc和θl(l∈{2,…,J})得到稀疏信息^θl(l∈{2,…,J}),并由此将观测yl(l∈{2,…,J})分解为yl=yc+^yl,其中观测信息^yl的个数为^n=tkl.当共同观测值yc都迁移到节点Sl+1时,则w(el)=tkc,同时将观测信息^yl直接传输给接收节点.在WSN中,进行基于压缩感知的自适应数据融合方案的主要步骤如下:首先,在传感器融合节点上对每个汇聚的节点信息进行编码.然后,计算各个节点在G=(V,E)中进行数据融合的能量开销,根据自适应函数选择数据融合树上每一层中能耗最小的节点,并找到这个能耗最小的数据融合路由.如果对每个节点都进行数据融合,需要消耗较多的融合能量并且融合能量大于该条路由因为进行数据融合所减少的传输能耗,这种情况下进行数据融合反而增加了能量开销,所以要根据每个节点的融合能量,采用数据融合时进行自适应调整,以达到网络总能耗最优.最后,不进行数据融合的直接携带该节点的感知数据传输到下一个节点,进行下一级的数据融合.
如果重复执行数据融合过程,直到信息回到Sink,则可得整个网络能耗为
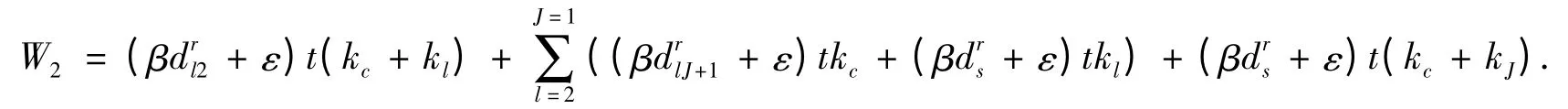
根据上面描述,将分布式压缩感知算法的网络传输总能耗W1和自适应的压缩感知算法中网络的总传输能耗W2进行比较:
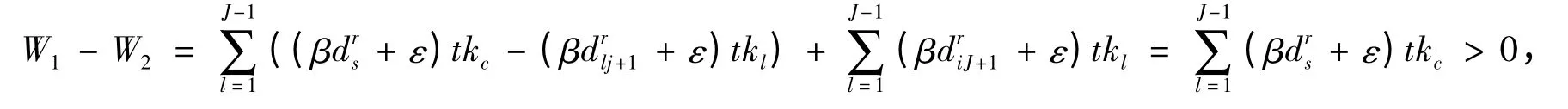
即W1>W2.
2.2 仿真实验
为了验证压缩感知方法在WSN中的网络传输能耗问题,本研究采用Matlab处理平台对两种算法进行了测试.首先,在实验中随机选取传感器节点分布在长宽均为60 m的区域,同时随机产生10~60的整数值作为源节点个数,两种算法所需的网络传输能耗相差不大,如表1所示.

表1 两种方法传输能耗比较Tab.1 Two methods transmission energy consumption comparison μJ
但是,当节点数不断增加时,由于信号重构的计算时间和复杂度相对增加,分布式压缩感知融合算法所需的网络传输能耗增加很快,而自适应压缩感知数据融合算法所需的网络传输能耗变化则不明显,具体情况如图1所示.其中,T1表示分布式压缩感知算法,T2表示自适应的压缩感知数据融合算法,水平轴表示节点个数,数值轴表示能量消耗.
根据实验结果可得,在随机产生的多个节点的多维信号的联合稀疏结构中,根据数据融合理论,基于压缩感知的自适应数据融合方法在编码和解码中应用WSN感知的多维信号集合将不同的观测信息直接传输给节点,传输过程中只携带共同观测信号,有利于传输和融合,从而大大减少了网络传输能耗.
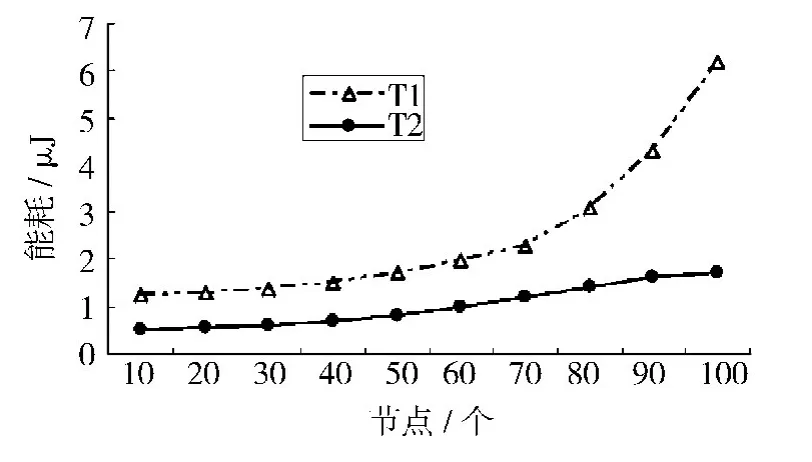
图1 两种算法网络传输能耗比较Fig.1 Two algorithm network transmission energy consumption comparison
3 结论
从WSN中常用的分布式数据融合方法进行分析,为了减少数据融合本身的能量开销和数据传输所消耗的能量开销,将压缩感知理论应用到WSN的分布式数据融合中,并分析一种基于分布式压缩感知的自适应数据融合路由算法,最后将基本的分布式压缩感知数据融合方法和自适应的分布式压缩感知数据融合方法在网络能耗方面进行比较,得到自适应的分布式压缩数据融合方法在网络能耗方面的开销要小得多.
[1]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2]Haupt J,Nowaak R.Signal reconstruction from noisy random projections[J].IEEE Transactions Information Theory,2006,52(9):4036-4048.
[3]Baron D,Wakin M B.Sarvotham S,et al.Distributed Compressed Sensing[EB/OL].http://www.dsp.rice.edu/drorb/pdf/DCS112005.pdf.2005.
[4]Sun N,Lian Q S.Data aggregation technique combined temporal-spatial correlation with compressed sensing in wireless sensor networks[C].IEEE International Conference on Intelligent Computing and Integrated Systems(ICISS2011),The Proceedings of IEEE,Guilin,2011:781-785.
[5]Chen Y,Nasrabadi N M,Tran T D.Hyperspectral image classification using dictionary based sparse representation[J].IEEE Transaction on Geoscience and Remote Sensing,2011,49(10):3973-3985.
[6]Zhang L,Wei D Z,Pei CC.Kernel sparse representation-based classifier[J].IEEE Transactions on Signal Processing,2012,60(4):1684-1695.

