澳大利亚未来潜艇外形特点分析
刘聪尉,吴方良,李 环,彭娅玲
(中国舰船研究设计中心,湖北 武汉 430064)
0 引言
二战之后,美国在借鉴德国先进潜艇技术的同时,着手开发潜艇水动力性能,基于当时可提供的最佳水动力性能研究,旨在设计具有最小水下阻力的潜艇。1953年12月5日,第1艘“大青花鱼”号常规动力潜艇完工,水下最高航速达33 kn。突出特点是:水滴形外形,大直径低转速螺旋桨,声呐置于流线型鼻部处。
早在1868年,瑞典造船学家Nystrom即提出用1/4可以调整指数的椭圆及一段可调整指数的抛物线来描述水滴形回转体母线线型的公式。理想形状的各站直径是随船长连续变化的。在水滴形最大截面处增加一段平行中体能够减小吃水,增加甲板空间布置的灵活性,便于潜艇水声探测设备如舷侧阵声呐的布置,还能在潜艇大规模建造时节省艇体中段的建造成本和建造时间。如美国的“鲣鱼”级(1958)攻击核潜艇,日本的“夕潮”级 (1979),“春潮”级 (1989)常规潜艇等都是采用结合水滴形和平行中体的设计方案。
“柯林斯”级 (1993)常规动力潜艇是澳大利亚建造的最新一级常规潜艇,其总体性能、武器威力、安静性和自动化水平都属世界先进水平。
2026年左右,“柯林斯”级潜艇将面临淘汰和废弃,具有优良阻力性能和噪声性能的下一代潜艇[1-2](即2026年潜艇)正处于设计阶段。
2020-2050年的战略环境要求潜艇具备高端性能,集中表现在远程化、精细化。下一代潜艇要实现扩大作战半径和増加战略用途的目标,与“柯林斯”级相比,增加武器数量和导弹装载能力,船员数量仍保持在45~55人。考虑到并发作战能力和战备冗余,2026年潜艇数量在6艘以上[3]。
澳大利亚计划于2011年开始潜艇初步设计。在此之前着手研究某些关键技术:外形设计和材料,电池技术、性能和存储,不依赖空气推进技术,推进系统,水下、水面和空中无人驾驶作战工具及其与潜艇对接接口。其中,外形设计的目的是建造一艘阻力和流噪声最小的潜艇,具体是以下3个目标:航行尽可能安静,实际阻力最低,从而获得更大的最高航速和更少的燃料消耗;使流经首部流体状况尽可能好,流噪声不会影响首部被动声呐的正常工作;内部体积配置更灵活,增加甲板空间。
相比“柯林斯”级,2026年潜艇将增加直径,缩短长度,以期获得满足阻力要求的最佳长径比。由于直径的加大,在部分船长上增加一层甲板,吃水增加但不会影响在船坞或港口附近的航行,增加下潜深度和骨架强度,提高执行任务时潜艇的隐蔽性。
最引人注目的是,鼻部形状的设计借鉴NACA翼型,同样条曲线配合,选取合适的厚度和长度比,以期在一定长度上保持层流边界层。2026年潜艇未严格采用水滴形外形设计,原因是什么呢?
笔者认为,水滴形公式简单,仅有2个控制参数,缺乏对艇形参数的全面性规定,不容易根据总布置等要求调整控制参数从而调整型值,必须在全船长范围实现变化。而翼型可通过搭配不同长度样条曲线,在相当长的范围内调整型值,满足设计要求,且对排水量影响不大。
数值计算方法能有效开展潜艇外形与流场特性的关联研究,在已知艇体形状特征下精确预报流场(速度场、压力场和噪声场)特性,为潜艇概念设计阶段得出阻力小、噪声低的最佳潜艇设计方案提供评价依据。
随着计算机计算性能的突飞猛进,潜艇流场的数值模拟蓬勃发展,成为潜艇研制中必不可少的技术手段。国内外很多学者在潜艇粘流数值计算领域做了大量细致深入的工作[4~7]。吴方良等[8]采用不同的湍流模型、边界条件对SUBOFF模型主艇体的7种网格模型进行了三维粘性流场数值模拟,对数值模拟方法的可靠性和准确性进行了验证和考核。
本文首先介绍澳大利亚2026年潜艇外形,定性分析其快速性能;用数值计算方法对潜艇模型周围流场进行数值模拟,分析使用CFD进行计算潜艇水动力特性时应注意的问题;选取具有可比性的水滴型潜艇模型的数值模拟结果进行比较,证实翼型有助于保持鼻部边界层层流,效果接近水滴型。合理选择水滴型控制参数,可以找到与2026年潜艇鼻部最为接近的某一水滴形型值公式。从理论上说明翼型配合样条曲线在保持水滴形外形优良水动力性能的同时,还具备易于调整,便于加工等优势。在平衡潜艇设计的各项边界条件,选取水动力特性、总体布置、可靠性、经济性等各项性能指标时,要综合考虑。彼此兼顾,达到较优的平衡状态。
1 澳大利亚2026年潜艇外形
新潜艇采用流线型回转体船型,具有几何形状简单、优良的流体静力动力特性等优点。回转体船型是潜艇艇形之一。人们一直致力于寻求各种有效的方法来降低流线型回转体的阻力、流噪声和改善其水动力性能,其中最有效的手段是外形设计。本文先以外形设计准则[9]对2026年潜艇的水动力性能做定性分析。
对于没有平行中体的潜艇,CP=0.6时总阻力和形状阻力最小,而2026年潜艇平行中体长度为32 m,有效减小了形状阻力,使L/D和CP能在相当大的范围内变动时,引起的总阻力变化未必很大。当长径比在6~8之间某一个值时,能获得一个最小的总阻力,但这一区域总阻力随长径比变化并不明显。2026年潜艇的主尺度如下:排水量为3968 t,艇长L=70.2 m,直径D=9.6 m,长径比L/D=7.3,菱形系数CP=0.76。
合适的鼻部形状设计对整个潜艇的外形设计至关重要。主要从阻力和噪声2个方面影响潜艇性能。理想的鼻部形状,应该保证鼻部绕流速度梯度较小,对层流起稳定作用,在较长距离下保持层流边界层,推迟转捩点,从而减小摩擦阻力系数。边界层稳定性理论[10]指出,压力梯度对层流边界层稳定性起着决定性的影响,压力沿下游方向减小有稳定作用,而压力增加导致边界层失稳。另一方面,空泡是宽带强噪声源,产生极强的自噪声和辐射噪声,必须设计无空泡鼻部线型。同时,由于转捩区自身是一个强噪声源,湍流压力脉动诱发噪声远严重于层流,鼻部形状设计应在足够长度上保持层流,限制流噪声,能使得鼻部声呐在潜艇航行时正常接收信号。因此,2026年潜艇尽量避免在鼻部开口,并重新布置鱼雷管,使其未穿过鼻部。
鼻部起始段采用等比例放大后的NACA 0016翼型型值。NACA4位数字翼型有相同的基本厚度分布,第1位数字代表f,表示最大百分比弯度;第2位的1/10表示最大弯度位置,代表p;后2位表示百分比厚度c。NACA 0016是一个无弯度、厚16%的对称翼型。
翼型厚度
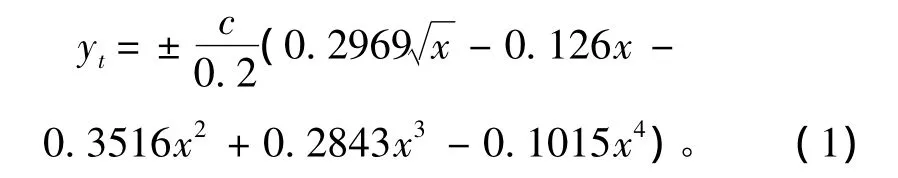
式中:yt为相对厚度,x为相对长度。
由式(1)可以得到NACA 0016的型值,从而得到x/L=0~0.11的鼻部形状。为了减缓发生在x/L=0.11处压力的上升,用样条曲线向后延伸外形至船长16 m处,然后和圆柱体平行中体相连接。压力最小处约发生在2026年潜艇船长x=7 m处,有可能在4 m之前保持层流边界层。
尾部采用与“柯林斯”级潜艇相同的圆锥角和长度,以避免产生大漩涡,保持良好的水动力性能,并提高螺旋桨来流质量。
2 潜艇三维流场计算数学模型
2.1 计算对象
本文进行的三维粘性流场模拟计算对象有2个:一是对2026年潜艇按1∶20的缩尺比得到的模型;二是同2026年潜艇模型主尺度 (艇长和直径)、湿表面积和排水量基本相等的水滴形潜艇光体模型。
2.2 控制方程
不可压缩流体的连续性方程:
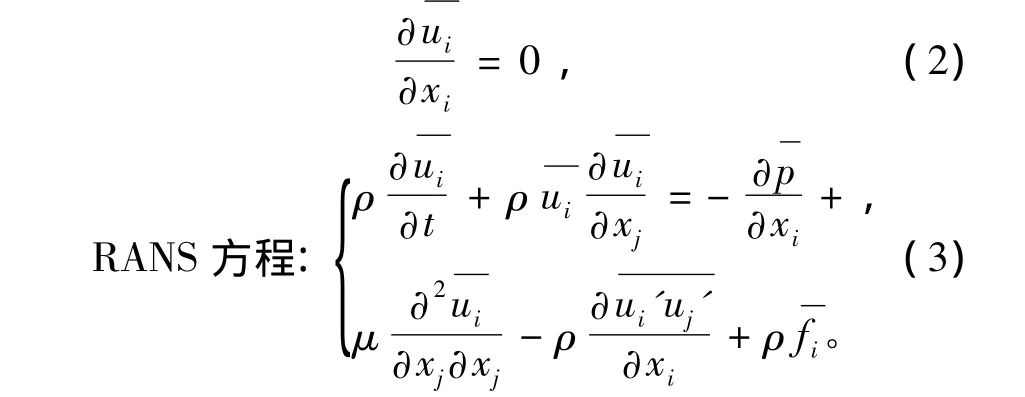
式中:ui为雷诺平均速度;ui'为脉动速度;脉动速度相关项称为“雷诺应力”。
2.3 湍流模型
考察RANS方程式(3),可知,方程中有关于湍流脉动值的Reynolds应力项属于新的未知量,要使方程组封闭,必须对Reynolds应力作出某种假定,即建立应力的表达式 (或引入新的湍流模型方程),通过这些表达式或湍流模型,把湍流的脉动值与时均值联系起来。由于没有特定的物理规律可以用来建立湍流模型,所以目前的湍流模型只能以大量的实验观测结果为基础。
根据对Reynolds应力作出的假定或处理方式不同,目前常用的湍流模型有如下几类:Reynolds应力方程模型、标准k-ε湍流模型、RNG k-ε湍流模型、k-ω湍流模型。本文选用RNG k-ε湍流模型。
RNG k-ε湍流模型中,通过在大尺度运动和修正后的粘度项体现小尺度的影响,而使这些小尺度运动有系统地从控制方程中去除。所得到的k方程和ε方程为:

2.4 数值计算方法
采用有限体积法离散控制方程和湍流模式。对于压力方程采用标准的离散格式进行离散;对于动量方程、湍流方程、雷诺应力方程,均采用二阶迎风格式进行离散,压力速度耦合迭代采用SIMPLEC算法。
2.5 边界条件
计算流场域的边界由进流边界、出流边界、壁面边界和控制域边界组成。
进流边界条件:取在回转体首前方5倍艇体直径处。采用速度进口边界的条件。u=U0,v=w=0,其中U0为来流速度。在使用各种k-ε模型对湍流进行计算时,需要给定进口边界上k和ε的估算值,该值对于计算结果的准确程度和计算收敛性有较大的影响,目前没有理论上的精确计算公式。按照吴方良等[7]的建议,计算采用 k≈u/100,ε≈(10~20)k。
出流边界条件:取在回转体后方距尾端点15倍艇体直径处,压力出流边界条件。采用自由出流边界条件或压力出流边界条件计算获得的艇体表面的剪应力系数是一致的,但是艇体表面的压力系数则有一定的差别,其中采用压力出流边界条件计算所获得的压力分布与试验数据更加吻合[7]。
壁面边界条件:采用无滑移边界条件。
控制域条件:取5倍艇体最大直径。速度为没有受到扰动的边界条件。
2.6 计算网格
在靠近潜艇表面的区域,需要满足壁面函数的适用要求,网格需要划分得足够紧密;在潜艇的首部、尾部,曲率变化剧烈,计算网格需加密;而在潜艇中部,曲率变化缓和,计算网格可适当稀疏。
3 计算结果与讨论
3.1 不同雷诺数下2026年潜艇模型计算结果比较
首先在3种来流速度条件下对2026年潜艇模型的流场情况进行模拟。各工况情况及使用ITTC-57公式估算摩擦阻力系数Cf1结果见表1。

表1 2026年潜艇模型计算条件及估算摩擦阻力系数Tab.1 Computational conditions of submarine 2026’s model and estimated friction drag coefficients
从Fluent计算结果中读出主艇体的摩擦阻力系数Cf2、压差阻力系数Cp和总阻力系数Ct。具体数值见表2,其中ΔCf为2种方法所得摩擦阻力系数的相对误差。
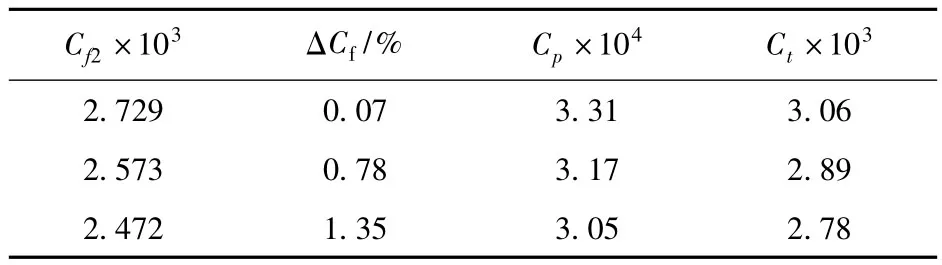
表2 不同雷诺数下2026年潜艇模型计算结果Tab.2 Computed results of submarine 2026’s model under different Regnolds number
由表2可知,随着来流速度增大,Cf2减小,Cp减小,Ct也减小。数值模拟所得Cf2略大于从ITTC-57公式计算的Cf1。
速度变化引起阻力变化的主要原因是改变摩擦阻力,即速度增加,摩擦阻力下降。因为压差阻力系数主要和艇形有关,对于某一固定艇体形状,改变航速,压差阻力相差不大。
Y+是第一层网格质心到壁面的无量纲距离,与速度、粘度、剪应力等有关系。表达式为:
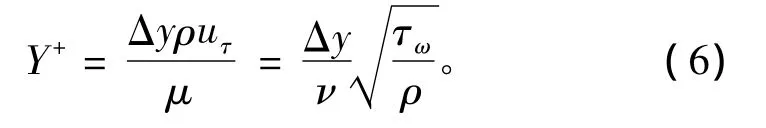
其中:u为流体时均速度;uτ为壁面摩擦速度;τw为壁面切应力;Δy为到壁面的距离。沿模型中纵剖面线上Y+分布如图1所示。
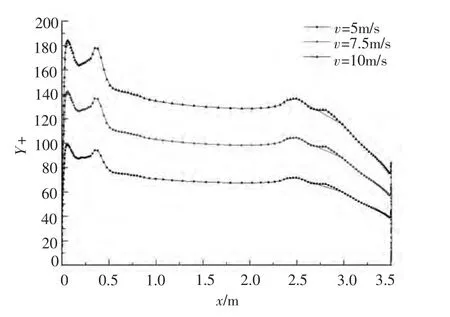
图1 不同速度下沿潜艇模型中纵剖面线Y+分布Fig.1 Distribution of Y-plus along the zero buttock in different velocities
由图1分析可知,同一结构化网格划分的Δy不变,来流速度的增大导致uτ(τw)增大,Y+随之增大。数值模拟和经验公式计算之间差别的增大正是由于数值模拟的τw准确性变差导致的。
无论是层流边界层,还是湍流边界层,其厚度随局部雷诺数的增大而减小。当速度增加过大时,网格划分的Δy应该减小,确保Y+不会超出对数律成立的范围。
3.2 两种潜艇计算结果比较
在U0=10 m/s,Re=3.50×107的条件下,对水滴形潜艇模型进行模拟。2026年潜艇和水滴形潜艇外形比较如图2所示。
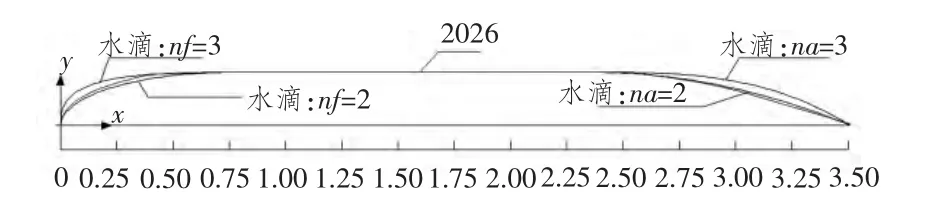
图2 2026年潜艇和水滴型潜艇纵剖线形状比较Fig.2 Comparison of Submarine 2026’s longitudinal profile shape with two Teardrop-submarines
其中水滴形潜艇形状控制参数分别取2和3时,2026年潜艇鼻部形状处于二者之间,说明可以找到与2026年潜艇鼻部最为接近的某一水滴形型值公式。后文计算取水滴形形状控制参数值为2,即
2种潜艇模型计算结果见表3,其中S为模型湿表面积;▽为排水量;N为数值计算网格数;为壁面Y+平均值;Cf1为公式估算摩擦阻力系数;Cf2为数值计算摩擦阻力系数;ΔCf为2种方法所得摩擦阻力系数的相对误差;Cp,Ct分别为数值计算得到的压差阻力系数和总阻力系数。
比较主尺度基本相等的A,B两模型Cf分布曲线如图3所示。纵坐标Cf=2τw/ρU02,其中 τw为回转体表面剪应力。
A,B两模型Cp分布曲线如图4所示。在艇长0.55~2.3 m的范围内,曲线分布几乎相同,但在前后两部分,差异较大。压力梯度对层流边界层的稳定性影响最大;顺流方向的压力降低有利于边界层的稳定,而压力上升则会导致层流边界层的不稳定。在入流段,从驻点开始,水流速度增加,压力降低。模型A的边界层稳定性应优于模型B。用最小压力处估计转捩点位置,模型A的转捩点可能会在模型B之前。Teardrop-2-2。为了表述方便,用A,B分别标记将2026年潜艇和Teardrop-2-2潜艇。
比较可知,由于湿表面积基本相等,摩擦阻力系数基本相等;进流段和去流段船体型线曲率变化和棱形系数对潜艇的压阻差力影响较大,两模型相差4.8%,总阻力相差0.51%,基本是由于外形的变化导致形状阻力系数改变引起的。
回转体进流段和去流段棱形系数有所不同。模型A,B相比,模型A的进流段棱形系数较大,去流段棱形系数较小。从中纵剖面线来看,模型A在进流段曲率变化先大后小,去流段曲率变化先小后大。
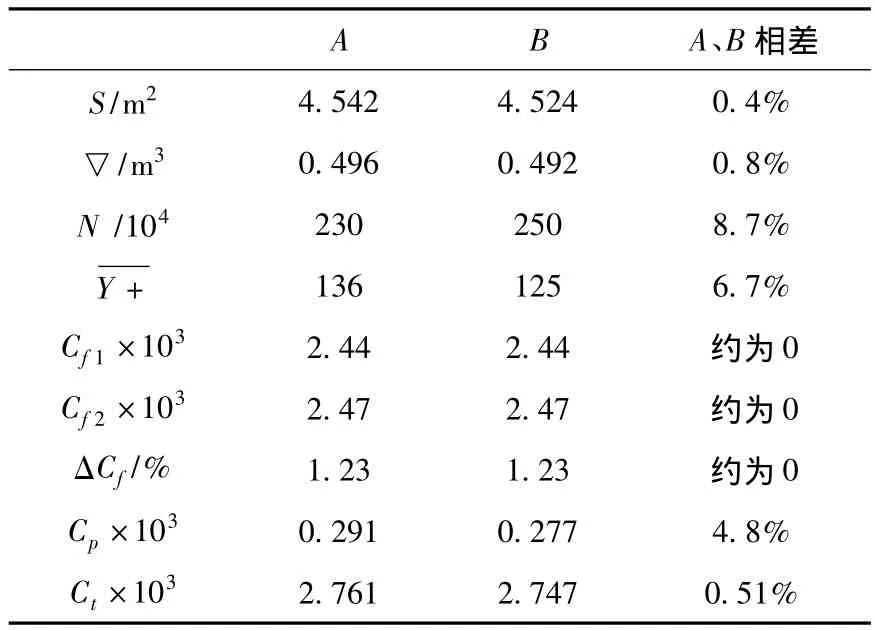
表3 相同雷诺数下2种潜艇模型计算结果Tab.3 Computed results of two submarine models under the same Reynolds number
模型A在x/L=0.11即艇长0.35 m处摩擦阻力系数和形状阻力系数都有极大的变化,在图中可以看到明显的高峰,可能是由于NACA翼型同样条曲线过渡的连续性不如水滴形函数那样令人满意。模型A首部Cp的绝对值并不大,还不至于产生空泡。
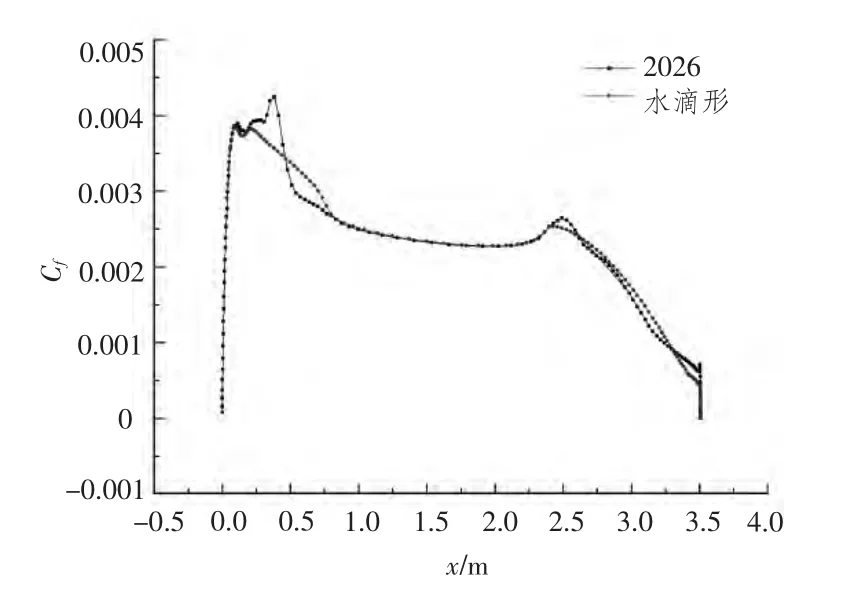
图3 潜艇表面摩擦阻力系数分布对比Fig.3 Comparison of distributions of surface friction drag coefficient
在去流段,模型A,B形状曲线在x/L=0.74,艇长L=2.6 m处相交。在交点之前,模型A曲率变化较大,交点之后,模型A曲率变化较小。这同Cp分布曲线的变化和交点是统一的。模型A的Cp曲线增大略先于模型,可能是由于较早出现的流动分离。去流段棱形系数比较大的模型B,尾部Cf曲线变化较为平缓,相反,去流段棱形系数比较小的模型A,则变化比较陡峭。
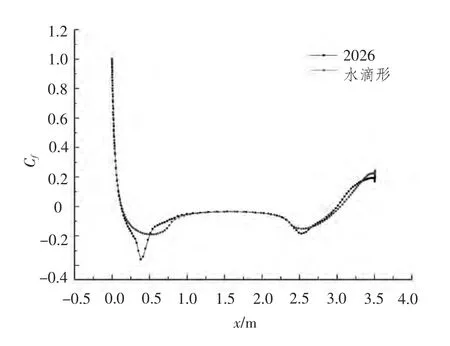
图4 潜艇上表面压力系数分布对比Fig.4 Comparison of the distributions of surface pressure drag coefficient
A模型Cp曲线下的面积同B模型Cf曲线下的面积相差较小,因而粘压阻力也差距不大。
4 结语
本文着重分析了澳大利亚下一代常规动力潜艇——2026年潜艇的外形特点和水动力特性。水滴形潜艇具有最佳的阻力特性,先验的结论是2026年潜艇阻力性能不会优于水滴形,通过数值模拟定量的分析了二者的差距并得到以下结论:
1)2026年潜艇外形设计合理,符合潜艇外形设计各项准则,与水滴形潜艇阻力性能的差距在于形状阻力,这和形状关系密切。形状的变化,直接引起艇体表面各处压力系数的变化;
2)艇体表面各处压力系数同对应处型线曲率的连续性有关。2026年潜艇鼻部翼型厚度公式同样条曲线的不连续导致压力系数突变,降低了快速性和隐身性,负压力系数绝对值过大会可能引发空泡。通过最小压力处预估转捩点,发现2026年潜艇具备达到预期目标的条件:在艇长4 m之前保持层流边界层,提高声呐性能;
3)表面压力梯度同曲率变化有关。通过比较2种潜艇表面压力系数变化和曲率变化规律,定性的结论是曲率变化剧烈 (平缓)处表面压力梯度大(小)。通过优化线型来控制边界层的分离,减少尾流区是减小压差阻力的有力手段;
4)考虑到翼型可能会比水滴形易于加工,性能相差不大,可以考虑采用翼型结合样条替代水滴型,但曲线曲率变化一定要光滑。
5)ITTC-57公式证实了本文采用的数值计算方法的可行性。但值得注意的是,对模型进行网格划分后,数值计算的准确性并非一成不变的。雷诺数增加后,由于数值模拟的τw的准确性变差,数值模拟和经验公式所得摩擦阻力系数的相对误差增大。在工程实际中,不同速度下网格特性都要保证满足Y+不会超出对数律成立的范围,即11.5~30<Y+<200~400;
6)潜艇设计的边界条件包含水动力特性、隐秘性、总体布置、作战能力、通信能力、可靠性、经济性等诸多方面,选取各项性能指标时,要综合考虑。彼此兼顾,达到较优的平衡状态。
[1]JOUBERT,P.N..Some aspects of submarine design part 1- hydrodynamics[R].Australia:Defence Science and Technology Organisation Technical Report DSTO-TR-1622,2004.
[2]JOUBERT,P.N.Some aspects of submarine design part 2- hydrodynamics[R].Australia:Defence Science and Technology Organisation Technical Report DSTO-TR-1920,2006.
[3]PETER B.A brief on the arising from consideration of the requirements for a future submarine capability for Australia[R].Australia:Submarine Institute of Australia,2007.
[4]BULL P.The validation of CFD predictions of nominal wake for the SUBOFF fully appended geometry[C],Proceedings of 21st Symposium on Naval Hydrodynamics,Trondheim,Norway,1996,1061 -1076.
[5]YANG C I,BETHESDA.Numerical simulation of three -dimensional viscous flow around a submersible body[C].Proceedings of 5th International Conference on Numerical Ship Hydrodynamics,Hiroshima,Japan,1989,59 -70.
[6]邱辽原,石仲堃,侯国祥.轴对称回转体绕流场数值模拟[J].华中科技大学学报,2004,32(10):46 -48.QIU Liao-yuan, SHI Zhong-kun, HOU Guo-xiang.Numericalsimulation ofthe flow over axisymmetric revolution[J].Journal of Huazhong University of Science and Technology,2004,32(10):46 -48.
[7]邱原,石仲堃,周凌,等.回转体三维绕流场数值计算[J].中国造船,2006,47(4):1 -7.QIU Yuan,SHI Zhong-kun,ZHOU Ling,et al.Numerical simulation of the 3D viscous flow field over a revolution body[J].Shipbuilding of China,2006,47(4):1-7.
[8]吴方良,吴晓光,许建,等.潜艇主艇体三维粘性流场数值计算方法研究[J].中国造船,2009,50(2):12 -21.WU Fang-liang,WU Xiao-guang,XU Jian,et al.Method of numerical calculation of the 3D viscous flow field over a submarine main hull[J].Shipbuilding of China,2009,50(2):12-21.
[9]沈国鉴.潜艇设计原理[M].上海:上海交通大学出版社,1988.SHEN Guo-jian.Principle of submarine design[M].Shanghai:Shanghai Jiaotong University Press,1988.
[10]H.史里希廷.边界层理论[M].北京:科学出版社,1991.H.Schlichting.Boundary-layer Theory[M].Beijing:Science Press,1991.

