大点线距数据网格化方法研究——以达来庙地区高精度磁测数据为例

，,2，

(1.中国地质大学(武汉)资源学院，湖北 武汉 430074； 2.中国地质大学地质过程与矿产资源国家重点实验室，湖北 武汉 430074)

0 引 言

大点线距数据主要是指测点距、测线距较大的地球物理数据，这些数据往往都是大比例尺数据。而这些地球物理数据在解释之前，需要经过数据网格化处理。不同网格化方法的使用对数据结果会产生影响，即空间内插模型不同，插值结果不同。常用的数据网格化方法有线性插值法(Watson,1992)、三角网法(刘天佑,2004)、最小曲率法(Briggs,1974)、反距离加权法(唐泽圣,1999)、克里格法(王仁铎等,1988)、张力样条法(唐泽圣,1999;王颖等,2011)等。针对这些方法，王颖等(2011)利用航空磁测数据网格化测试认为张力样条法适用于航测数据；刘兆平等(2010)认为数据量小于1 000个的情况下克里格法和最小曲率法最可行；而葛志广等(2010)在利用高精度磁法数据网格化测试后发现采用反距离加权插值法、最近邻点法、径向基函数法进行网格化,灰色区域负异常呈“块”状或孤立异常点分布,效果不理想。在大点、线间距的数值插值方面，前人利用了高精度磁法数据或航测数据，使用诸多方法测试，而在这些数据网格化中，等值线往往会呈现沿测线方向的“串珠”结构。就这个问题，目前研究不多，谢汝宽等(2013)在航磁数据网格化中提出了双方向测线型数据的网格化方法，取得了较好的效果。

在前人研究的基础上，使用Oasis montaj平台提供的三角网法、距离倒数加权法、双向线法、克里格法对达来庙地区高精度数据进行网格化，结合当地地质特征，通过参数设置和方法调整，交叉验证后总结出该平台下适用于该类数据网格化的方法，并解决数据沿测线方向呈现的“串珠”结构的问题。

所用数据为达来庙地区1∶5万高精度磁测数据，研究区域出露的地层有上石炭—下二叠统宝力高庙组：为灰-灰褐色安山岩、灰紫色英安质-流纹质火山熔岩及火山碎屑岩；石炭纪似斑状黑云母斑岩，第四系全新统主要为角砾层，岩屑层，砂土层。出露的侵入岩为石炭纪中粗粒黑云母二长花岗岩、细粒二长花岗岩、中粗粒黑云母花岗岩及中细粒黑云母花岗岩；侏罗纪灰紫红、灰肉红色中细粒花岗闪长岩。脉岩类包括中酸性、基性脉岩均有出露。区内与矿床成因关系密切的侵入岩主要为斑岩类。

区域上构造主要呈北东、北北东向展布，其中岩体和地层受构造控制非常明显，也多呈北东、北北东向产出。其次较发育的是北西向构造，再次为近东西向、近南北向与北北东向构造。断裂构造一般数十千米，小者数千米—几百米，主要形成于古生界—中生界。测线沿北西向布置。测点距离40 m，测线间距100 m。

目前，针对数据插值检验的方法主要是交叉验证法(高艳芳等,2012)。该方法首先需要预留若干数据样本点，然后对这些数据点作出预测，计算所有估计值与实际测量值的误差，从而判断插值方法的优劣。交叉验证即通过对已知的N个点的观测数据，计算和分析网格化后每个观测点上数据的残差来进行数据网格化质量评估。数据残差即网格化后的评估值Zm,i与实际观测值Ze,i之差。评估一个好的插值模型，一般选用可以反映利用样本点数据的估计灵敏度和极值效应的均方根误差(RMSE)，其值要最小或较小，从而来确定插值模型的好坏。

(1)

能总体反映估计误差的大小的平均相对误差(MRE)：

(2)

可以估算可能的误差范围的平均绝对误差(MAE)：

(3)

1 三角网法

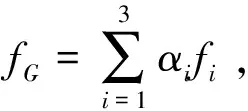
(4)

利用Oasis montaj软件对数据进行网格化处理。在进行三角网网格化中需要设置不同的重复次数(因为TIN程序在任何(X,Y)位置能处理的数据点都不超过1个,所以需要对重复Z值进行选择，选项是所有值求和或者使用平均值)和插值方法(本次选线性插值)。利用实验数据，在该软件下进行测试，结果如图1。

通过对数据网格化后并绘制三角网，三角网呈规则分布。验证结果如表1。

根据判断原则，从表中信息可以得出：(1) 三角网法在很大程度上尊重了原始数据，插值误差都接近0,应用效果较好；(2) 三角网图中显示了该方法沿测线方向进行插值，没有发现跳三角的现象；(3) 从垂向一阶导数图发现，异常呈线性，三角网法网格化后能反映出异常特征。

图1 三角网法试验结果

表1 三角网法交叉验证结果

2 距离倒数加权法

距离倒数插值方法是加权移动平均方法的一种(张瑞新等,1991)。假设未知点x0处属性值是在局部邻域内所有数据点的距离加权平均值，加权移动平均方法的计算如式(5)：

(5)

(6)

式中，权重系数由函数φ(d(x,xi))计算，要求当d→0时φ(d)→1，一般取倒数或负指数形式；d-r、e-d、e-d2,其中,φ(d(x,xi))最常见的形式是距离倒数加权函数，形式如式(7)：

(7)

式(7)中，xj为未知点，xi为已知数据点。

在Oasis montaj软件中进行距离倒数加权法需要进行下列参数设置：加权幂、加权坡度、搜索半径。

需要说明的是：距离倒数加权函数根据离开定义搜索半径的距离来指定平均权重：1/(距离幂+1/坡度)，其中距离的单位是网格图单元的单位。在该模块里，系统所使用的幂的默认值是2，坡度的默认值是1，这样将生成一个钟形权重函数。这里权重在0距离是有限的，所以这里需要坡度>0。坡度降低会使函数变平，使原网格图单元的点权重增加，图像变得平滑。

如此便可以通过对这些参数的调整来对数据进行更好的网格化处理。试验结果如图2。

图2 距离倒数加权法试验结果

根据上面不同参数的设置可以看出：在幂指数为2、坡度为1时，搜索半径不同，产生的效果不同；同样，当幂指数不同时，产生的效果也不同。通过设置参数，幂指数为2、坡度为1时，当搜索半径为数据网格单元的4倍、5倍、6倍时数据效果相近；同样，在幂指数为2、坡度为0.5时，数据效果相近。对其效果进行验证(表2)。

表2 距离倒数加权交叉验证结果

通过判断原则，分析表2中的信息得出：(1) 幂指数为2、坡度系数为1时，搜索半径小的情况下，数据网格化较好；幂指数为2，坡度系数为0.5时，情况相同。在该方法中搜索半径影响了数据网格化质量；(2) 在高精度磁测数据中，可取网格单元的4～5倍来控制数据质量。而幂指数和坡度是控制数据网格化效果是否圆滑的参数。

选幂指数为2、坡度系数为1、搜索半径为88时，作垂向一阶导数图(图3)。

图3 距离倒数加权结果

从图3中发现：使用距离导数加权法虽然能在网格化时突出一些北东向特征，但在作垂向一阶导数后，图像沿测线方向呈带状分布，应用效果并不理想。

3 双向线法

双向线网格化又叫做测线网格化方法(谢汝宽等,2013)，是Oasis montaj软件中常用的数据网格化方法之一，其主要用于对平行测线或者近似平行测线的数据网格化。双向线法中所指的双方向是对测线数据先进行某一方向进行插值，再沿垂直于前一插值方向进行插值。在Oasis montaj中，双向线网格化需要2个步骤来完成：(1) 每条线沿原始测线插值，并使用观测数据在每个需要的网格线与测线交叉点处产生数据值；(2) 每条测线的交叉点再沿测线方向插值，产生网格点上的值。在这个过程中，该软件中提供的插值方法有线性、最小曲率、Akima、最邻近法。此外，在二次插值前还可以通过网格图的正确方向来强调数据中的地质趋势，即调整网格图方向。

Akima插值方法是在2个实测点之间进行插值，但同时还需要与这2个点相近的4个实测点上的观测值(Akima,1970)。设置过实测点Pi(xi)和Pi+1(xi+1)的三次多项式为：

y=p0+p1(x-xi)+p2(x-xi)2+p3(x-xi)3

(8)

式(8)中，p0=y1；p1=t1；p2=[3(y2-y1)/(x2-x1)-2t1-t2]/(x2-x1)；p3=[t1+t2-2(y2-y1)/(x2-x1)]/(x2-x1)2；y1、y2分别为点Pi和Pi+1上的函数值；t1、t2分别为点Pi和Pi+1上的斜率，而每个点的斜率t由附近5个点确定。

根据研究区的数据情况，数据测线呈北西向，地质构造为北东向展布。因此，在网格化时对数据参数需要进行调整，考虑设置数据方向为45°。使用Akima和线性插值对数据进行网格化，并作垂向一阶导数图(图4)。

通过试验发现，该方法适用于测线型数据，且测线数据网格化后效果较好，突出了测线垂直方向上的异常情况。分别选取双向Akima插值和双向线性插值法进行验证(表3)。

表3 双向线法交叉验证结果

根据判断原则，结合表中信息可知：(1) 2种插值方法的使用，对数据结果影响不大，但双向Akima方法较优于线性法；(2) 该方法的使用受测线数据方向影响，根据原理，该方法更适用于垂向测线数据插值，所以在使用中要注意测线方向的调整；(3) 从垂向导数图发现，2种方法效果相当，都能较好地反映北东向异常的特征。

图4 双向线法试验结果

4 克里格法

(9)

式(9)中，h为滞后距，N(h)为数据在[f(xi),f(xi+h)]的对数。

利用克里格法一般是先对已知数据做实验变差函数，再用理论变差函数与实验变差函数进行拟合。几种常用理论变差函数所用的模型如下。

(1) 球状：

(变程a′=a) (10)

(2) 指数模型：

(变程a′=3a) (11)

(3) 高斯：

在Oasis montaj软件中,使用克里格法网格化同样是通过调整实验变差函数，再使用理论变差函数模型进行套合。利用普通克里格法将磁测数据进行网格化，数据测线沿北西向展布，进行实验变差函数结构分析发现，该结构为球状模型，因此再利用球状模型理论变差函数进行套合。考虑到数据各向异性的特征，构造走向为北东向，所以设置该方向上的权重，优先对北东向进行插值网格化。参数如下：块金值为0，拱高为130，变程为750，方向为45，方向权重为4 (各向异性)。

图5 变差函数图

经过变差函数调整和其他参数设置并对结果作垂向一阶导数(图6)。

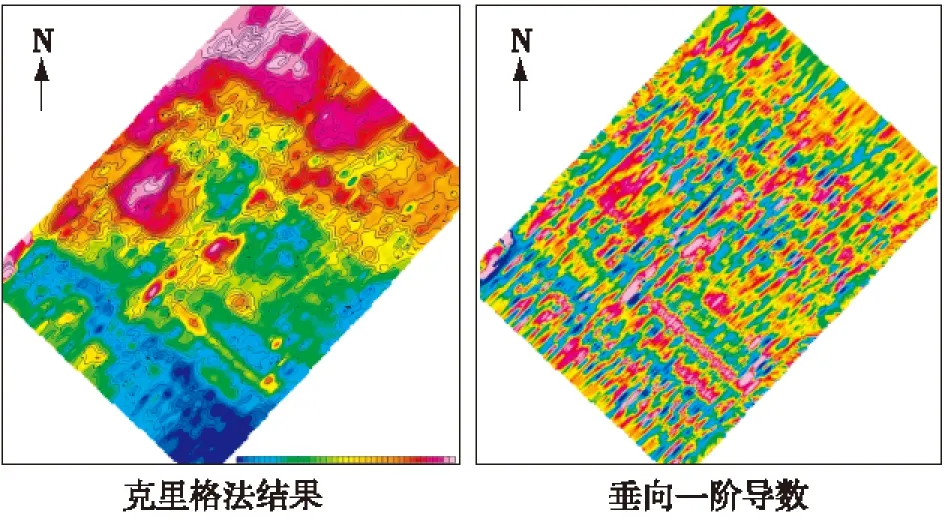
图6 克里格法试验结果

利用克里格法发现，通过调整变差函数和方向，消除了沿测线方向上的部分“串珠”结构，而从导数图像也能看出其北东向异常特征(表4)。

表4 克里格法交叉验证结果

经过验证，克里格法误差也比较小，能突出方向上的特征。

5 结 论

利用内蒙古达来庙地区高精度磁测数据进行网格化测试，通过利用三角网法、距离倒数加权法、双向线法、克里格法对高精度磁测数据的网格效果分析得出以下几点结论。

(1) 三角网法最能反映原始数据情况，在高精度磁法数据使用线性三角网法能快速计算，得到网格化结构。但会产生一些沿测线方向的“串珠”结构，所以采用线性的方法插值效果较好，尤其是对于大点线类型的数据，线性三角网法效果较好。

(2) 距离倒数加权法受到幂指数和搜索半径的影响较大。大点线距数据由于数据本身测点测线距离比较大，所以要调整合适的幂指数和搜索半径，距离越大，搜索半径也要随之提高，这样才能更好地避免数据呈“串珠”状。经过测试后发现，根据达来庙地区地质构造概况，该区所使用的高精度磁测数据，如果采用距离倒数加权法，应该使用网格图单元大小4倍的搜索半径，从而取得相对合理的结果。对于大点线数据网格化，该方法并不作为最佳方法来选择。

(3) 双向线法是一种基于测线的网格化方法，在本次研究高精度数据网格化中，因数据是测线数据，选用该方法能得出较好的结果。而要利用双向线法必须选择合适的双向插值方法，在大点线距数据中，选用线性插值、Akima插值效果较好。此外，测线方向的控制对该方法应用效果有很大影响。由于构造方向呈北东向，所以在方法使用时应考虑测线方向性问题。对于大点线数据，如果能控制好测线方向和选择合适的插值方法，该方法较为适用。

(4) 克里格法的使用必须考虑到变差函数。在本次研究高精度磁测数据中，通过调整合适的变差函数来得到较好的插值模型，能较好地使用克里格法。在大点线距数据网格化的使用中，套合变差函数模型必须考虑方向性，对于各向异性的数据，使用方向权重能较好地体现出构造方向上的异常特征。

(5) 大点线数据的网格化，要使数据最符合原始异常可以选择线性三角网法，要得到最优网格效果可以选择使用双向线法，而克里格法可以突出一些方向性，距离倒数加权法可以不常用。

郭良辉,孟小红,郭志宏,等.2005.地球物理不规则分布数据的空间网格化法[J].物探与化探,29(5):438-442.

葛志广,宋俊杰.2010.高精度磁法数据网格化方法的选取[J].工程地球物理学报,7(2):169-172.

高艳芳,陈实,冯斌.2012.交叉验证在离散数据网格化时的应用[J].物探化探计算技术,34(5):619-621.

刘天佑.2004.应用地球物理[M].武汉:中国地质大学出版社.

刘兆平,杨进,武炜.2010.地球物理数据网格化方法的选取[J].物探与化探,34(1):93-97.

苏姝,林爱文,刘庆华.2004.普通Kriging法在空间内插中的运用[J].江南大学学报：自然科学版,3(1):18-21.

唐泽圣.1999.三维数据场可视化[M].北京:清华大学出版社.

王仁铎,胡光道.1988.线性地质统计学[M].北京:地质出版社.

王颖,祝民强,乔康宁.2011.航测数据处理中的空间插值方法比较[J].测绘与空间地理信息，34(1):234-237,241.

谢汝宽,王平,郭华,等.2013.考虑航磁水平梯度变化的ΔT网格化方法研究[J].地球物理学报,56(2):660-666.

张瑞新,于汝绶.1991.距离加权法的完善及其在层状矿床储量计算中的应用前景[J].中国矿业大学学报,20(4):45-53.

AKIMA H.1970.A new method of interpolation and smooth curve fitting based on local procedures[J].Journal of the ACM,17(4):589-602.

BRIGGS C I.1974.Machine contouring using minimum curvature[J].Geophysics,39(1):39-48.

WATSON F D.1992.Contouring:A Guide to the Analysis and Display of Spatial Data[M].Oxford,UK：Pergamon Press.