基于自回归法的滑坡监测数据Kalman滤波的应用

徐爱功,张建龙,隋 心,刘 伟,张兆南

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.洛阳电子装备试验中心，河南 洛阳 471000；3.东北煤田地质局物探测量队，辽宁 沈阳 110101)

(1.School of Geomatics, Liaoning Technical University, Fuxin 123000, China; 2.Luoyang Electronic Equipment Test Center, Luoyang 471000, China; 3.Physical Exploration and Surveying Team, Northeast Coalfield Geology Bureau, Shenyang 110101, China)

基于自回归法的滑坡监测数据Kalman滤波的应用

徐爱功1,张建龙1,隋 心1,刘 伟2,张兆南3

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.洛阳电子装备试验中心，河南 洛阳 471000；3.东北煤田地质局物探测量队，辽宁 沈阳 110101)

介绍了卡尔曼滤波的基本模型，针对运动学方法以监测点位置参数、速率参数为状态向量，以加速度为噪声向量建立观测方程和状态方程的过程比较复杂。把自回归法引入状态方程和观测方程的建立中，并结合某露天矿滑坡动态监测数据分析了模型的应用。结果表明，滤波值和观测值之间差值保持在1～3 cm之间，滤波后图像较原观测值图像更为光滑，表明所建模型是合适的，能够反映滑坡动态变化过程，从而为矿滑坡监测预报提供数学工具。

自回归模型；卡尔曼滤波；滑坡；预报

我国露天矿数量众多，高陡边坡稳定性一直是影响露天矿生产安全的重要问题。据统计，不稳定边坡或具有潜在滑坡危险的边坡占边坡总长度可达15%～20%，甚至更高[1]。由于滑坡具有时间上的突发性和后果上的严重性，因而加强对滑坡体的监测，对滑坡作短期、中期和长期预报，具有重要的现实意义[2]。

Kalman滤波是美籍匈牙利数学家卡尔曼在滤波理论中引入状态空间分析方法提出的一种处理动态数据的方法，是一种线性无偏且以均方误差最小为准则的最优估计算法,由于其具有可递推实现，利于计算机运算等优点，已成为目前处理动态观测数据的一种常用方法。滑坡是一个动态发展过程，适合采用卡尔曼滤波处理观测数据，并作出预报。文献[3-6]在建立滤波模型时以监测点的位置、速率和加速度等参数构建状态向量、观测向量，这种方法能够反映变形体的运动状态，但是构造过程较为复杂。本文将监测点高程变化看做是一个依赖于时间的变量，监测前后各期之间具有一定的相关性，利用自回归法建立卡尔曼滤波的状态方程和观测方程，并在某露天矿滑坡动态数据处理中的应用做了研究。

1 Kalman滤波模型

1.1 Kalman滤波模型的建立

Kalman滤波方程的建立，需要已知系统模型和观测模型，并且要给出噪声的先验统计性质，以及系统状态的初始值。进而根据建立的方程实时获得系统的状态变量和输入信号的最优估值。下面给出离散Kalman滤波模型的建立过程[7]：

状态方程xk=Φk,k-1xk-1+Γk,k-1ωk-1.

(1)

观测方程zk=Hkxk+vk.

(2)

式中:Φk,k-1为状态转移矩阵；Γk,k-1为状态噪声系数阵；Hk为观测向量系数阵；ωk-1,vk分别表示状态噪声与观测噪声，且具有如下统计特性：

E(ωk-1)，E(vk)为ωk-1，vk的期望；Rωω(k,j)，Rvv(k,j)为ωk，vk的自协方差；Rωv(k,j)为ωk，vk的互协方差；E(x0)，var(x0)为已知的初值；R(x0,ωk-1)，R(x0,vk)为x0与ωk-1和vk的协方差。由于动态噪声和观测噪声均是零均值的白噪声序列，且互不相关,故以上建立的模型可以称为完全不相关的白噪声作用下的Kalman滤波。在满足均方误差最小的前提下可以得出以下滤波递推公式[7]：

状态估计校正

(3)

卡尔曼增益

(4)

误差协方差预测

(5)

误差协方差估计校正

Pk|k=(I-KkHk)Pk|k-1.

(6)

图1 卡尔曼滤波示意图

1.2 状态方程和观测方程的建立

在处理滑坡监测数据时，状态方程和观测方程的建立是关键的一步，尽管Kalman滤波模型状态方程和观测方程的建立方法很多，但多数文献是以监测点的运动学模型为基础建立的。例如，文献[3-5]是以监测点的位置参数(水平坐标和高程)及三维坐标速率作为状态向量，以三维坐标加速度为噪声向量建立的。文献[6]将某时刻变形量对上一时刻展开成泰勒级数取至三次方，仍然是采用运动学模型。该方法能够反映变形体的运动状态，但方程建立过程较为复杂。本文采用一种较为简单的方法建立状态方程和观测方程，即自回归法，避免了计算点位变化过程的速度和加速度，建立过程如下：

自回归模型

xk=η1xk-1+η2xk-2+…+ηnxk-n+ωk-1.

(7)

η1,η2,…,ηn是n阶加权系数，ωk-1是白噪声序列[8]，将该模型引入Kalman滤波中。

令x1(k)=xk，x2(k)=xk-1…

xi(k)=xk-i+1，xn(k)=xk-n+1.

则状态方程为

即xk+1=Φk+1,kxk+Γk+1,kωk.

其中:

观测方程为

zk+1=[1 0 … 0]·[x1(k+1)x2(k+1) …

xn(k+1)]T+v(k+1).

即zk+1=Hk+1xk+1+vk+1.

其中：Hk+1=[1 0 … 0]。

至此，就完成了状态方程和观测方程的建立。

这里，对加权系数ηi(i=1,2,…,n)的求法通常有矩估计法、最小二乘法、最小方差法、极大似然估计法等[8]，通常采用最小二乘法，将式(7)改写成矩阵形式为

即V=Aη-L.

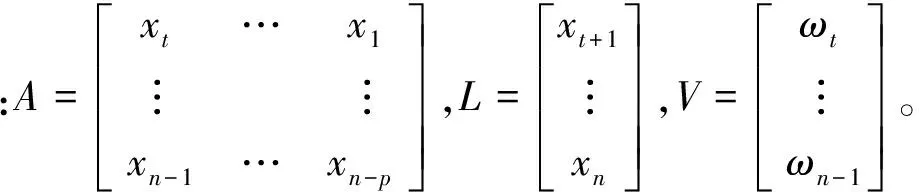
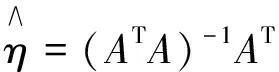
(8)

1.3 状态初值的确定

卡尔曼滤波是由一组递推公式给出的，在滤波前需要给定初值x0和P0。x0可以根据前面几组观测值给定，P0可以由初始测量值经过统计方式给出，通常P0应为对角阵[9]。

2 实例分析

2.1 概 况

阜新矿业集团白音华某露天矿位于内蒙古西乌珠穆沁旗境内，在不断开挖过程中边坡受采矿爆破影响强烈，加之大型机械作业震动及长期雨水侵蚀，以及不断堆积扩大的排土场对滑坡体压力不断增大[10]，稳定性逐渐变差，最终导致滑坡的发生。

通过监测获取的数据采用Kalman滤波模型处理。滤波模型是通过已知观测值建立的，模型系数矩阵在模型确定的前提下即可得到。本文首先采用某监测点前30期的高程观测值(见表1)求解自回归方程，建立基于自回归法的Kalman滤波模型，通过分析确定转移矩阵及观测矩阵，建立状态方程和观测方程。再对后面10期观测数据进行滤波，检验模型的正确性及滤波效果。

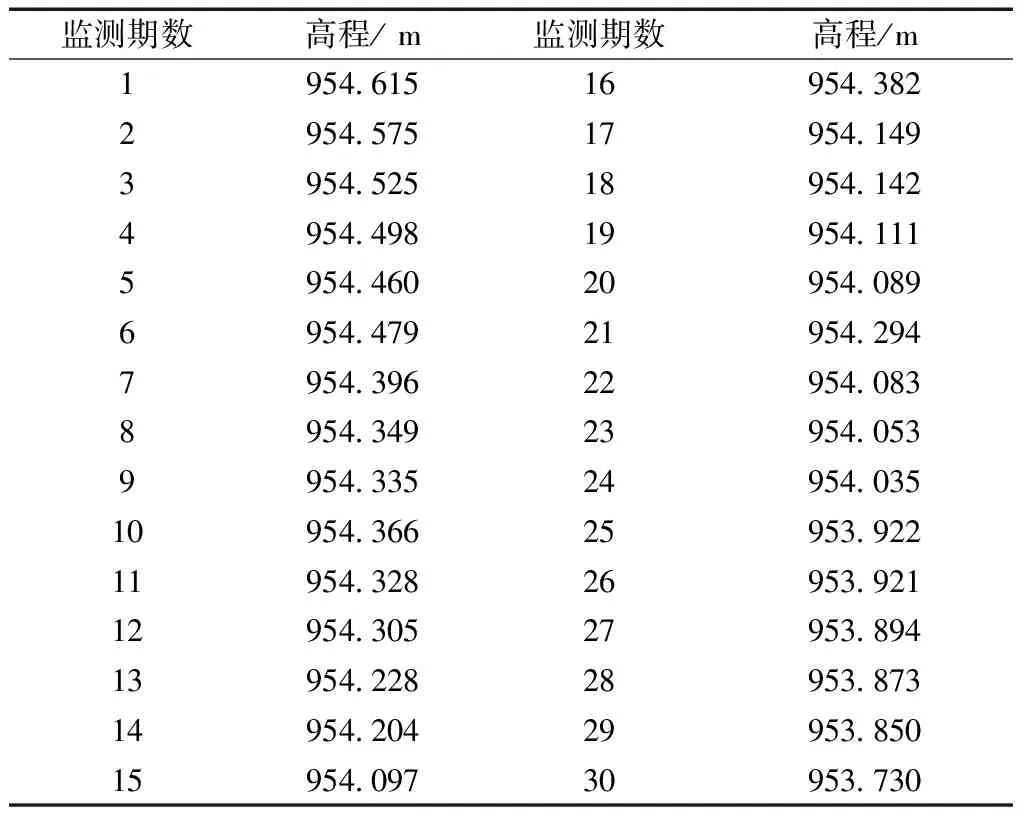
表1 某监测点各期观测值高程

2.2 模型建立

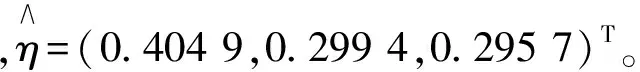
Γ=[1 0 0]T，H=[1 0 0].

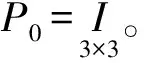
2.3 程序设计

由于Matlab具有变量定义简单、编程效率高、作图方便等优点[11]，故对上述建立的卡尔曼滤波采用Matlab进行程序设计，Kalman滤波程序如下：

clc;

close all;

z1=xlsread(′data.xls′,′sheet1′,′A1:A30′); %观测值

p0=eye(3); %初值方差阵赋初值

p=p0;

phik=[0.4049,0.2994,0.2957;1,0,0;0,1,0]; %状态转移矩阵

Qk=eye(3); %状态噪声矩阵

Hk=[1,0,0]; %观测向量系数矩阵

Rk=1; %观测向量噪声矩阵

x0=[954.615,954.575,954.525]′;

Xk=x0; %状态矩阵赋初值

for k=1:30

Pk=phik*p*phik′+Qk; %误差协方差

Kk=Pk* Hk′*inv(Hk*Pk*Hk′+Rk); %增益矩阵

Zk=z1(k);

Xk=phik*Xk+Kk*(Zk-Hk*phik*Xk); %最优估计值

x1(k)=Xk(1);

p=(eye(3)-Kk*Hk)*Pk; %误差协方差估计校正

end

2.4 数据分析

由图2、图3可以看出滤波值和原始测量值保持一致的下降趋势，且最大偏差为6.28 cm，是由于第16和21两次观测值可能含有较大误差，大部分差值保持在1～4 cm。滤波后图像比原测量曲线要平滑，说明模型建立的是合理的，能够达到消除测量中干扰误差的目的，经过预测、修正所得到的滤波最优估值能够更好地反映滑坡动态变化过程。

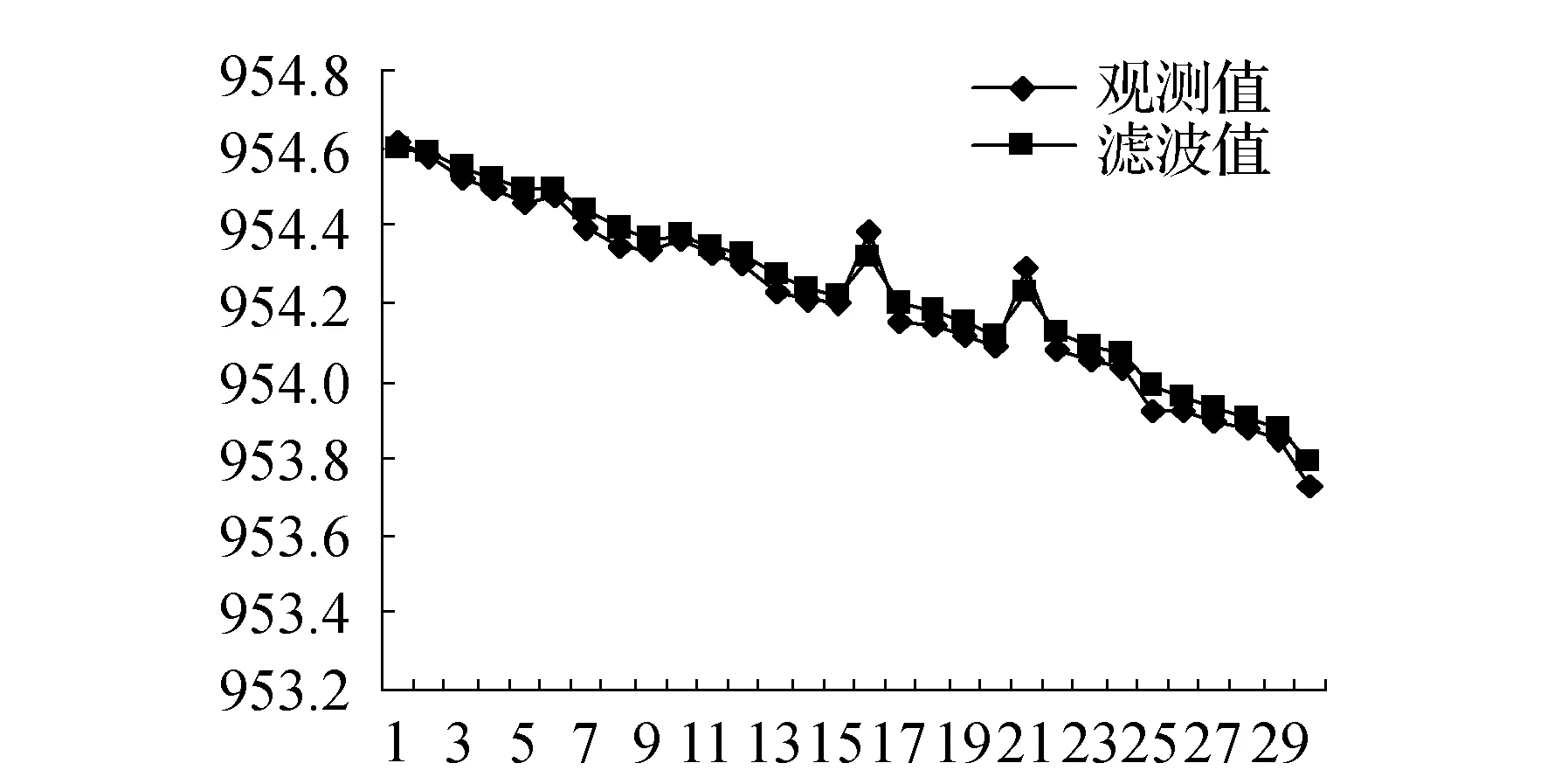
图2 观测值与滤波值对比

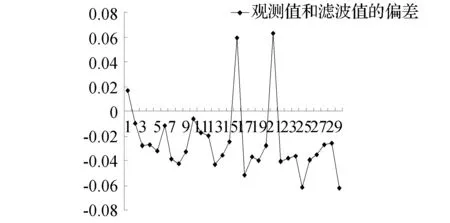
图3 观测值与滤波值的偏差

通过以上建立的滤波模型再对未来10期(31～40期)观测数据做出预测，初值的确定采用以上数据最后3期，即x0=[953.873,953.850,953.730]。观测值与估计值如表2所示。观测值与估计值对比和差值如图4、图5所示。可以看出，仅预测初始2期偏差较大，这是由于递推过程初始值选取与实际观测值之间有一定的偏差造成的，之后几期偏差都在1～3 cm，说明初值的选取仅会影响前面较少几期的预测结果，而不会对之后几期有影响；滤波估计值呈一致的下降趋势，而原始观测值由于存在观测误差并没有呈一致下降趋势，说明滤波后能够较好反映滑坡动态发展规律，滤波对滑坡的预测效果良好。

表2 未来10期高程观测值与估计值对照

图4 未来10期观测值与估计值对比

图5 未来10期观测值与估计值的差值

3 结 论

通过以上模型的建立及数据处理结果分析可以得出以下结论：

1)将自回归法引入状态方程和观测方程的建立过程中，使得滤波模型的建立过程简单化，避免采用运动学方法的复杂性。

2)Kalman滤波把参数的估计和预报结合起来，有效消除观测噪声，通过参数的不断修正，增强模型适应不断获得的数据，可以实时计算滤波值，也可以对未来几期做出预测，为预测滑坡的变形发展提供依据。

3)如果观测不平稳，一些观测值有较大起伏或观测值含有较大误差，滤波偏差会较大；初值选取与实际观测值有一定偏差时，预报结果前面较少几期偏差会较大，所以应用Kalman滤波也是有一定的局限性。

[1]姚颍康，周传波，郭廖武，等.深凹露天矿山岩质边坡稳定性预测[J].金属矿山，2008(3):42-45.

[2]张正禄，黄全义，文鸿雁，等.工程的变形监测分析与预报[M].北京：测绘出版社，2007.

[3]高雅萍，冯晓亮.GPS变形监测动态数据处理中卡尔曼滤波的应用[J].海洋测绘，2006,26(4)：36-38.

[4]许国辉，余春林.卡尔曼滤波模型的建立及其在施工变形测量中的应用[J].测绘通报，2004(4):22-23.

[5]陈帅，赵丽，李超，等.卡尔曼滤波在坝体变形监测中的应用[J].全球定位系统，2011(5):83-84.

[6]陆付民，王尚庆，李劲.离散卡尔曼滤波法在滑坡变形预测中的应用[J].水利水电科技进展，2009,29(4):6-9.

[7]刘胜，张红梅.最优估计理论[M].北京：科学出版社，2011：129-164.

[8]张树京，齐立心.时间序列简明教程[M].北京：清华大学出版社，北方交通大学出版社，2003：49-54.

[9]修延霞，候凯.卡尔曼滤波在大坝变形监测中的应用[J].城市勘测，2010(1):92-94.

[10]温德娟，滕寿仁，杨子荣.白音华3号露天矿矿坑充水因素研究[J].煤炭技术，2006,25(7):97-98.

[11]刘卫国.Matlab程序设计教程[M].2版.北京：中国水利水电出版社，2010.

[责任编辑：刘文霞]

Application of Kalman filtering to the landslide monitoring data procession based on auto-regression method

XU Ai-gong1， ZHANG Jian-long1， SUI Xin1， LIU Wei2， ZHANG Zhao-nan3

It introduces a basic model of Kalman filtering.The kinematic method establishes the observation equation and state equation based on location parameters and rate as the state vector, acceleration as the noise vector.The auto-regression method is introduced into the establishment of the state equation and observation equation, simply compared with the kinematic method.Taking one opencast mine landslide dynamic monitoring data as an example, it analyzes the model application.The results show that the deviation of filtering value and observed value is between 1 to 3cm, and the filtering image is smoother than the original observation image.It shows that the model is appropriate, and it can reflect the dynamic change process of landslide.So the method provides a powerful mathematical tool for this opencast mine landslide monitoring and prediction.

auto-regression method; Kalman filtering; landslide; forecast

2013-08-30

精密工程与工业测量国家测绘地理信息局重点实验室开放基金资助项目(PF2012-8)；现代城市测绘国家测绘地理信息局重点实验室开放课题资助项目(20111203W)

徐爱功(1963-)，男，教授，博士生导师.

P642

：A

：1006-7949(2014)09-0052-04

(1.School of Geomatics, Liaoning Technical University, Fuxin 123000, China; 2.Luoyang Electronic Equipment Test Center, Luoyang 471000, China; 3.Physical Exploration and Surveying Team, Northeast Coalfield Geology Bureau, Shenyang 110101, China)