基于改进Dijkstra算法的机场抢修决策模型研究
邓 涛,熊自明,王青山
(1.信息工程大学 地理空间信息学院,河南 郑州 450052;2.解放军特种作战学院,广东 广州 510500)
基于改进Dijkstra算法的机场抢修决策模型研究
邓 涛1,熊自明2,王青山1
(1.信息工程大学 地理空间信息学院,河南 郑州 450052;2.解放军特种作战学院,广东 广州 510500)
机场抢修决策模型是实现机场道面快速抢修的核心环节,传统的机场抢修决策模型普遍存在模型假设脱离实际、计算结果在实际中难以应用等缺点。文中将GIS技术应用于机场抢修决策,提出基于限制区域的Dijkstra改进算法的最优路径模型,在此基础上,探讨“单对单”、“多对单”和“多对多”3种模式下机场抢修决策模型的建立方法。
机场抢修;决策;GIS;Dijkstra算法;模型
机场抢修决策模型是实现机场道面快速抢修的核心环节,是机场抢修部门根据机场道面修复所需材料和设备情况、预置物资仓库的储备情况,对材料和设备的有序流动作出的科学计划安排。机场抢修决策主要研究预置仓库如何给机场调拨运输所需修复材料和设备的问题。
传统的机场抢修决策模型普遍存在模型假设脱离实际、计算结果在实际中难以应用等缺点。GIS特有的一些功能可以弥补传统方法的不足,能使决策过程更加快捷、方便,结果更加精确、实用。
1 机场区域最优路径模型
最优路径模型是GIS中的重要网络空间分析算法,应用范围较广。但是,在机场区域最优路径计算与普通路径优化算法存在一个最大的不同点就是:机场区域最优路径的计算是在一个相对较小的区域范围内进行。因此,本文针对小区域范围内Dijkstra算法路径搜索效率低的问题,结合机场抢修业务实际改进优化经典的Dijkstra算法。
1.1 Dijkstra算法
最优路径问题最经典的算法是Dijkstra算法,其他路径优化算法大都是基于此算法的改进,如A*算法。Dijkstra算法实际上是一种图上标记作业法,每次计算完成一个搜索节点就产生一个标记,直至所有路网节点被标记。为了便于理解,本文结合一个具体实例解释Dijkstra算法的基本原理和步骤。
假设某区域有5个后方仓库或场站,其位置分别是A1~A5,另外还预置物资仓库,其所在位置P0,如图1所示。现需5个仓库或场站给预置物资仓库补充物资,求出从预置物资仓库到5个仓库或场站各自的最短路径及其路程。图1中的数字是各资源点或预置物资仓库之间的距离。

图1 路网示意图
根据Dijkstra算法的原理,除去预置物资仓库P0作为搜索起点外,还须进行5轮搜索,每次搜索标记1个仓库或场站,具体搜索过程如下:
1)初始化P0并作标记,搜索与P0的邻近相通的节点有A1和A2,寻找到与P0距离最短的邻近相通节点A2并作标记,则最短路径为P0→A2,最短距离为1;
2)在已标记的节点P0,A2中寻找未作标记的邻近相通节点,找到节点A1、A3和A4,3个节点中距离最短的为节点P0到A1,给A1作标记,最短路径为P0→A1,最短距离为2;
3)在已标记的节点P0,A1,A2中寻找未作标记的邻近相通节点,找到节点A3和A4,两个节点中距离最短的为节点A4,给A4作标记,最短路径为P0→A1→A4,最短距离为5;
4)在已标记的节点P0,A1,A4,A2中寻找未作标记的邻近相通节点,找到节点A3和A5,两个节点中距离最短的为节点A3,给A3作标记,最短路径为P0→A2→A3,最短距离为6;
5)在已标记的节点P0,A1,A2,A4,A3中寻找未作标记的邻近相通节点,只有节点A5且为最后一个节点,直接给A5作标记,最短路径为P0→A1→A4→A5,最短距离为8。
至此,预置物资仓库P0到各仓库或场站的最短距离均已算出,从预置物资仓库P0到各仓库或场站的最短路径均可以反推前一个节点得出。根据优化结果绘出最短路网示意图如图2所示,图中矩形框内所示为对应节点到P0的最短距离。
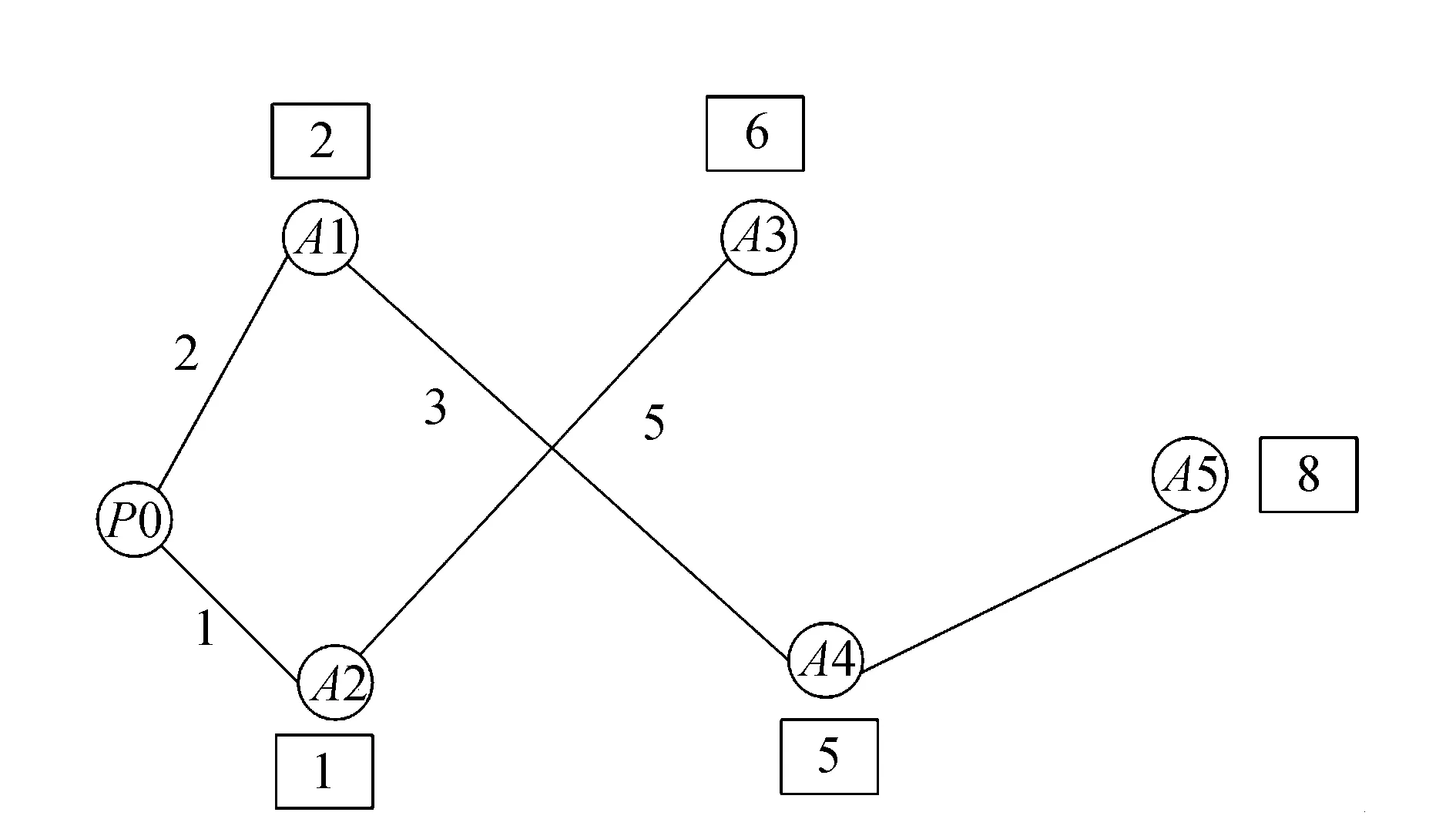
图2 最短路网示意图
1.2 限制区域的Dijkstra改进算法
由于机场区域最优路径的计算是在一个相对较小的区域范围内进行,并不需要搜索所有的道路网节点。因此针对此问题,本文提出一种限制区域的Dijkstra改进算法,其基本思路如图3所示。

图3 限制矩形区域的Dijkstra搜索
图3中,Dijkstra算法搜索最短路径时几乎是以源点为圆心的圆向外扩展,直到找到目的地为止,所以Dijkstra算法搜索的范围几乎相当于以源点和目的地为半径的整个圆的范围。限制矩形区域的Dijkstra改进算法的基本要点是:将算法搜索的范围限制在以源点和目的地连线为基础构造的一个外扩矩形范围内,由此可以大大减少算法的搜索范围。该矩形区域建立的方法是:
1)以源点和目标点的连线为X轴,以其垂直的方向为Y轴,以源点为原点建立直角坐标系。
2)矩形的长度LR为源点和目标点的连线长度LPB外扩合适的阈值K1确定,矩形的宽WR由阈值K2确定,即LR=LPB+2K1,WR=K2。通常阈值K1,K2可根据LPB来确定,即Ki=λi*LPB(i=1,2),其中λi为比例因子,可根据区域内道路的密集程度来确定,如果区域内道路较密可取值较小,如0.2,如果区域内道路较稀少可取值较大,如0.8,其他情况可介于两者之间。
限制区域的Dijkstra改进具体算法如下:
输入:研究区域D内的道路网拓扑数据,预置物资仓库P0坐标和空军后方仓库、场站或者机场B坐标。
输出:P0和B间的一条最短路径和最短路径的长度。
1)以源点P0和目标点B的连线为X轴,以其垂直的方向为Y轴,以P0为原点建立直角坐标系。
2)根据道路网的密度选择合适的阈值K1,K2构造限制区域的矩形。
3)在Dijkstra算法运算过程中,判断已标记的节点邻近相通节点是否在限制区域的矩形范围内,如果不在则置该节点的权重为最大值表示不相连通;如果在则按照Dijkstra算法继续运行。
4)输出P0和B间的最短路径和最短路径的长度。
2 “单对单”模式
“单对单”模式,是最简单的机场抢修保障模式,只有一个预置物资仓库和一个待抢修机场,是属于典型的两个固定地点之间寻求最优路径的问题。假设预置物资仓库为P0,需要抢修的机场为B,P0到B经过N个节点的路网,则其目标函数为
(1)
“单对单”模式的最优路径直接利用1.2中给出的模型求解即可。具体的抢修决策流程为:首先根据机场道面破坏状况评定模型确定机场道面修复所需材料和设备的种类、数量;然后在GIS中查询预置物资仓库中存储的材料和设备情况是否满足需求,如果满足需求则启动“单对单”抢修运输模式;最后利用机场区域最优路径模型计算最优运输路径,并给出经过的主要地名、路径长度等信息。具体流程如图4所示。

图4 “单对单”模式决策流程
3 “多对单”模式
“多对单”模式,是一种较复杂的机场抢修保障模式,有多个预置物资仓库和一个待抢修机场。在抢修机场确定的情况下,需要对当前参与保障的预置物资仓库的保障能力、空间分布及道路交通等信息进行分析,从多个预置物资仓库中选出最优的保障对象、保障品种和数量,明确其输送路线。
3.1 模型建立
假设某方向上,有1个待抢修机场B,对物资(为简化问题,将机场道面修复所需的材料和设备统称为物资)的需求量分别为Yk(k=1,2,…,s),s为物资种类,选定m个预置物资仓库承担其物资供应任务,分别是Pj(j=1,2,…,m),物资存储量分别为Rjk(j=1,2,…,m;k=1,2,…,s)。
利用机场区域最优路径模型,分别求出预置物资仓库Pj到机场B的最短路径距离,设Pj到B为短路径距离为dj(j=1,2,…,m),构建距离关系矩阵
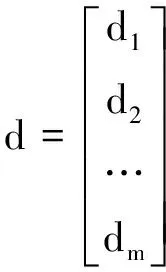
(2)
然后对距离关系矩阵d进行排序,根据就近保障原则,依次找到最小距离的预置物资仓库进行抢修保障,使得总距离最短。
(3)
3.2 模型实现
“多对单”模式机场抢修决策模型是根据道路交通条件进行的,模型实现主要有两种方法:
1)以待抢修机场所在地为运算起点。运用机场区域最优路径模型,从该点出发沿着与其相连通的道路进行搜索,对在搜索过程中遇到的预置物资仓库及其保障能力进行判断,如果预置物资仓库无保障能力或者不属于保障范围,则继续搜索,如果预置物资仓库具备保障能力则记录其相关信息(如地理位置、连接道路、物资储备情况),如果抢修所需物资的需求量已经得到满足则停止搜索,否则继续搜寻。其流程如图5所示。
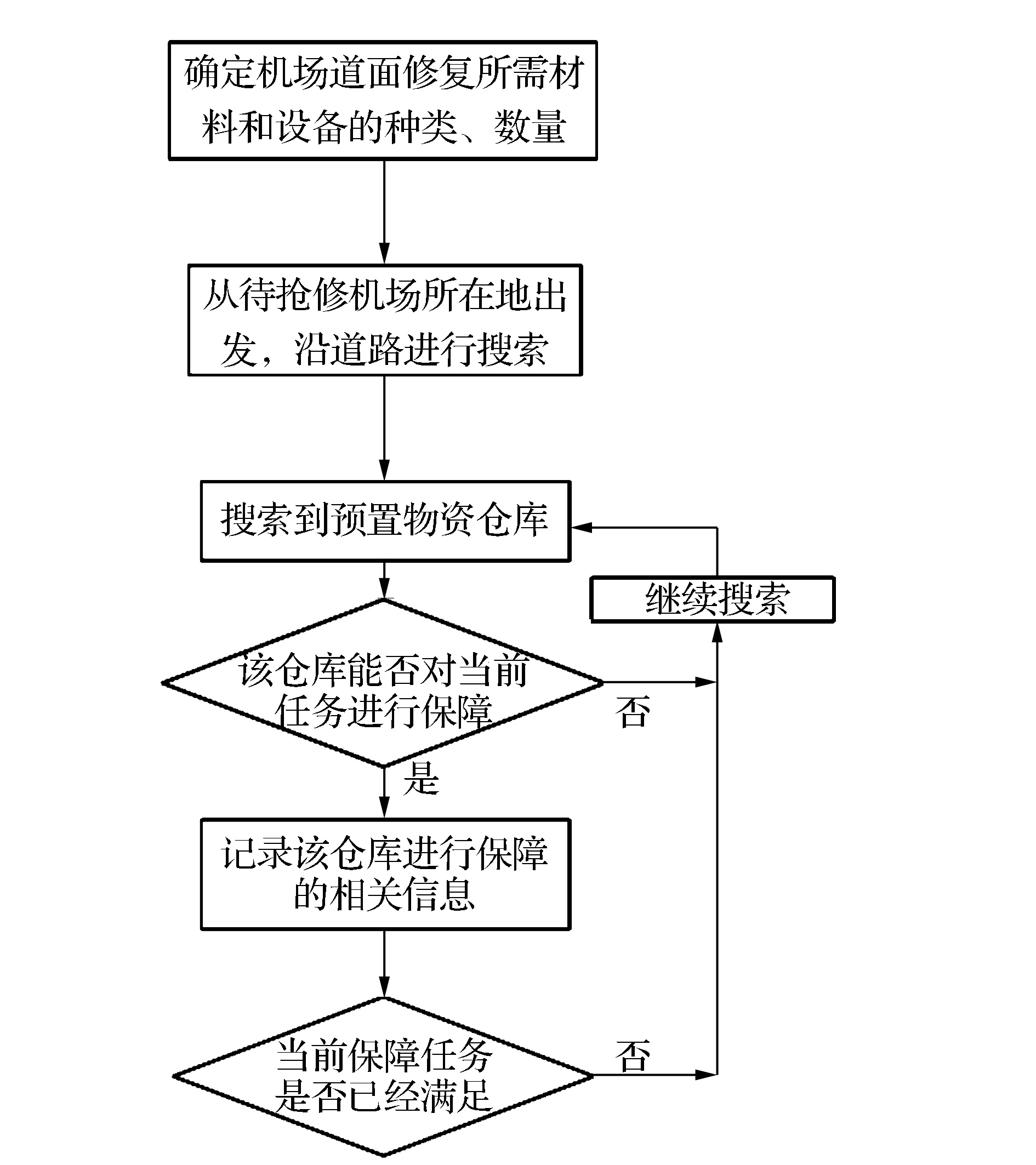
图5 “多对单”模式决策流程
2)以预置物资仓库所在地为运算起点。运用机场区域最优路径模型,获取所有参与保障的预置物资仓库与待抢修机场之间的距离关系矩阵,然后按照就近保障原则,优先选择距离最短的预置物资仓库,计算其物资种类、数量,如果不能满足保障任务,则继续选择剩下距离最短的预置物资仓库,直至满足抢修物资需求为止。
4 “多对多”模式
“多对多”模式,是最复杂的机场抢修保障模式,有多个预置物资仓库和多个待抢修机场,需要解决多个预置物资仓库和多个待抢修机场之间的优化保障问题。
4.1 模型建立
假设某方向上,有n个待抢修机场Bi(i=1,2,…,n),对物资的需求量分别为Yik(k=1,2,…,s),s为物资种类,选定m个预置物资仓库承担其物资供应任务,分别是Pj(j=1,2,…,m),物资存储量分别为Rjk(j=1,2,…,m;k=1,2,…,s)。
利用机场区域最优路径模型,分别求出预置物资仓库Pj到机场Bi的最短路径距离,设Pj到Bi最短路径距离为dji(j=1,2,…,m;i=1,2,…,n),构建距离关系矩阵
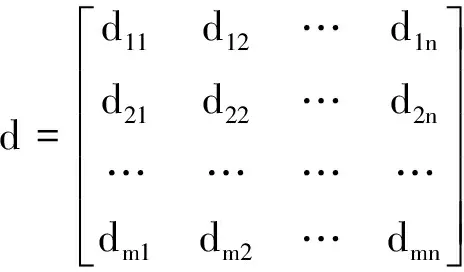
(4)
然后对距离关系矩阵d进行总排序,根据就近保障原则,依次找到最小距离的预置物资仓库进行抢修保障,使得总距离最短。
(5)
4.2 模型实现
“多对多”模式的模型基于GIS实现主要有两种情况。
1)各待抢修机场的抢修任务有优先级区分的情况。该情况下,依据待抢修机场的优先级依次进行物资调拨运输优化,即将“多对多”模式转化为“多对单”模式进行。
2)各待抢修机场的抢修任务没有优先级区分的情况。该情况下有两种实现方法:第一种方法是利用机场区域最优路径模型求出预置物资仓库与待抢修机场之间的距离关系矩阵,然后比较所有矩阵元素,按照就近保障的原则,即距离从小到大的顺序依次确定参与保障的预置物资仓库,直至需求任务完成;第二种方法是将待抢修机场所在地作为运算起点,从该点出发沿着与其相连通的道路进行搜索,对在搜索过程中遇到的预置物资仓库进行判断,如果不属于保障范围或无保障能力则继续搜索,否则将预置物资仓库的保障物资数量记录下来,如果保障任务已得到满足则停止搜索,否则继续搜索。具体流程如图6所示。
搜索完成后进行汇总,明确各待抢修机场由哪些预置物资仓库进行保障,各预置物资仓库的保障种类、保障数量以及这些预置物资仓库进行保障时的最优路径。

图6 “多对多”模式决策流程
5 结束语
本文将GIS中的基于改进Dijkstra算法的最优路径模型应用于机场抢修决策,给出“单对单”、“多对单”和“多对多”3种模式下机场抢修决策模型的建立方法,为机场抢修科学决策提供一个有效的方法。
[1]武军,王治.一种机场抢修预置物资仓库选址模型[J].基建优化,2006,28(3):91-93.
[2]万莉.基于GIS和最短路径算法的物流重心选址的研究[D].长沙:中南大学,2007.
[3]李庆奎,吕志平,李昌贵. 基于模糊理论的智能最优路径算法[J].测绘工程,2011,20(4):5-8.
[4]付金辉,赵军喜,高源. 基于灰色预测法的超市选址模型研究[J].测绘工程,2013,22(5):46-50.
[5]李元臣,刘维群.基于Dijkstra算法的网络最短路径分析[J].微计算机应用,2004,25(3):295-298.
[6]陈涛.车辆导航系统中大区域路径规划算法的设计与实现[D].郑州:信息工程大学,2005.
[7]王海梅.基于GIS的最优路径算法研究与实现[D].南京:南京大学,2008.
[8]AHN C W, RAMAKRISHNA R S. A genetic algorithm for shortest path routing problem and the sizing populations[J]. IEEE Transactions on Evolutionary Computation,2002,6(6):566-580.
[9]ZHAN F B, NOON C E. Short path algorithms: an evaluation using real road network [J]. Transportation Science,1998, 32(1):65-73.
[10]付梦印,李杰,邓志红.限制搜索区域的距离最短路径规划算法[J].北京理工大学学报,2004,24(10):881-884.
[11]王海涛,朱春生,安立国,等.野战机场抢修抢建机械群调度系统的研究与实现[J].机械制造与研究,2009,41(3):73-76.
[12]张仁平,刘奇韬.物资调拨运输优化模型及应用研究[J].物流技术,2009(3):85-87.
[13]李爱零.战时物资筹措与运送模型研究[D].西安:西安电子科技大学,2007.
[14]龚延成.战时军事物流系统决策理论与方法研究[D].西安:长安大学,2004.
[15]温伯威,王超峰,刘瑞雪,等.基于泛在网信息的城市应急疏散决策研究[J].测绘工程,2013,22(6):58-60.
[16]王华.利用组合技术的迪杰斯特拉算法改进探讨[J].测绘科学,2014,39(2):52-54.
[责任编辑:张德福]
Research on airport rapid repair decision-making model based on improved Dijkstra algorithm
DENG Tao1, XIONG Zi-ming2, WANG Qing-shan1
(1.School of Geographic Spatial Information,Information Engineering University, Zhengzhou 450052, China;2. Special Operations University, Guangzhou 510500, China)
The model of airport rapid repair decision-making is the key link in realizing airport rapid repair, while traditional airport rapid repair emergency decision-making has some shortcomings widespreadly, such as: the assumption is away from reality, the calculation results are difficult to apply to the practice,and so on. GIS technology is applied to the airport rapid repair decision-making, and proposed an optimal path model using restricted areas of Dijkstra algorithm. Discussion is made on the establishment method of this model under three patterns of “single to single”, “single to many” and “many to many”.
airport rapid repair; decision-making; geographic information system(GIS); dijkstra algorithm; model
2014-03-17
国家自然科学基金资助项目(41201390)
邓 涛(1984-),男,博士研究生.
P208
:A
:1006-7949(2014)10-0031-05

