非球形引力位中J3项对轨道的影响及应用
田家磊,赵东明,张中凯,范昊鹏
(1.信息工程大学 地理空间信息学院,河南 郑州 450052;2.信息工程大学 导航与空天目标工程学院,河南 郑州 450001)
非球形引力位中J3项对轨道的影响及应用
田家磊1,赵东明1,张中凯2,范昊鹏1
(1.信息工程大学 地理空间信息学院,河南 郑州 450052;2.信息工程大学 导航与空天目标工程学院,河南 郑州 450001)
地球的非球形引力摄动是人造卫星环绕地球飞行过程中所受到的摄动中较重要的一项。在人造卫星的精密定轨和卫星位置的预报中,人们往往对J2项比较重视,但是对于J3项的研究比较少。为了解J3项的性质,文中分析了非球形引力位中J3项对于卫星轨道的影响,通过严格的公式推导,得到J3项对轨道偏心率以及轨道倾角的影响,详细地介绍利用它形成冻结轨道的基本原理。通过数值实验对得到的基本理论以及应用进行验证。结果表明J3项是冻结轨道形成的重要因素。
J3项;冻结轨道;非球形引力摄动;轨道力学
在地球上空运行的人造地球卫星、航天飞机、飞机、热气球等各种飞行器,仍然会受到地球重力场的作用[1]。如果它们只是受到地球质心的吸引力,那么它们的飞行轨道将是以地球质心为其中一个焦点的椭圆。但是由于地球形状的不规则和内部质量分布的不均匀,引力的方向和大小发生改变,会造成飞行器的轨道偏离椭圆轨道。这种差别被称为地球的非球形引力摄动。
对于人造卫星来说,地球的非球形引力摄动是卫星在运动过程中所受摄动中比较重要的一项。在低轨卫星所受力中对轨道影响量级最大的是地球引力和地球的非球形引力[2]。地球的非球形引力摄动分为二项,一项是与经度无关的带谐项,一项是与经度有关的田谐项。在人造卫星的精密定轨(特别是在精度要求不太高的情况的下,如低轨卫星百米量级的定位要求)和卫星位置的预报中,人们往往会对带谐项比较重视[3],特别是主要带谐项—J2项,但是对于J3项的研究比较少。为了解J3项的性质,本文对非球形引力位中J3项对于卫星轨道的影响进行分析。
1 J3项影响分析
对于质心引力场,空间任何一点的引力位表述为
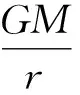
(1)
式中:G为引力常数,M为质点质量,r为空间测量点到该质点的距。相应的引力加速速度为[4]
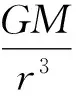
(2)
由于地球自转,又非旋转对称体,故空间任一固定点的引力位都要随时间变化,则相对于卫星运动的摄动函数的一般表达式为
F=V-V0=

Slmsinmλ].
(3)
这是星固坐标系中的形式,Me是地球质量,(r,λ,ψ)是卫星在该坐标系中的坐标分量(星心距、经度和纬度),R是参考椭球的赤道半径,Plm(sinψ)是缔合勒让德函数,Clm和Slm是非归一化的引力位展开式的谐系数。
如果仅考虑地球引力场带谐调和项的影响,既假定位函数是旋转对称的,则摄动函数可以表述为[5]
).
(4)
式中:Jl=-Cl0,μ=GMe,Pl(sinψ)是勒让德多项式。
对于地球来说,J2=O(10-3),J3、J4的量级要更小,由于J4以及之后的项不会引起与J2、J3影响不同的变化,而且量级很小,所以分析只考虑J2、J3项。那么摄动函数可展开整理为[6]
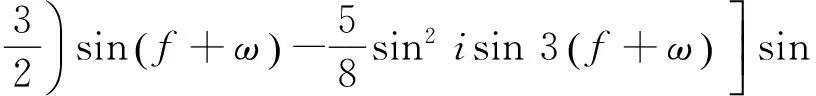
(5)
根据长期项、长周期项、短周期项分为F1、F2、F3:
(6)
从式(6)中F2可以看出,J3项引起长周期变化。对于地球来说,J3=J2(10-3)量级比较小,所引起短周期摄动的振幅很小。另一方面,长周期摄动的振幅是依赖于ω的长期变化,这有可能会导致振幅相对比较大。
2 应 用
冻结轨道是在1978年Orbit Analysis for SEASAT-A文章中第一次提出的,冻结轨道的构造是通过选择轨道倾角i、偏心率e和近点经度ω,使得e,ω随着时间变化保持为常数,因此也被称为拱线静止轨道。近年来冻结轨道被越来越多地应用到对地观测卫星系统中,因为它能使遥感卫星(作为一个质点)在不同时刻经过同一纬度时具有相同的运动特性,这就使得遥感卫星在不同时刻经过同一地区所得到的遥感图像具有相同的几何特性[5]。杨威廉[7-8]、刘林[9]和陈洁[10-11]对于冻结轨道的设计与控制有很多理论和实践的经验。
根据拉格朗日运动方程,在J2和J3项作用下的e和ω变化为
(7)
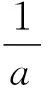

(8)
根据式(6)、式(7)、式(8)有
(9)
(10)
通过以上两式相除得

(11)
对式(11)积分,得到由J3项引起的对e的长周期摄动为
ω.
(12)
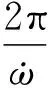
同样的方法可得到长周期摄动为
ω.
(13)
通过式(12)、式(13)可以清楚地看出,可以通过对轨道倾角i、偏心率e和近地点幅角ω的初始值进行特定组合的选择,能够使得e,ω随着时间变化保持为常数,以成为冻结轨道。
如果一组参数满足式(9)、式(10)的右端都为0,那么这一组参数就满足了冻结轨道的条件。根据程序可以搜寻表1中4组参数。

表1 4组冻结轨道参数
通过程序模拟了第二组条件下,轨道的演变,如图1~3所示。

图1 偏心率随时间的变化趋势
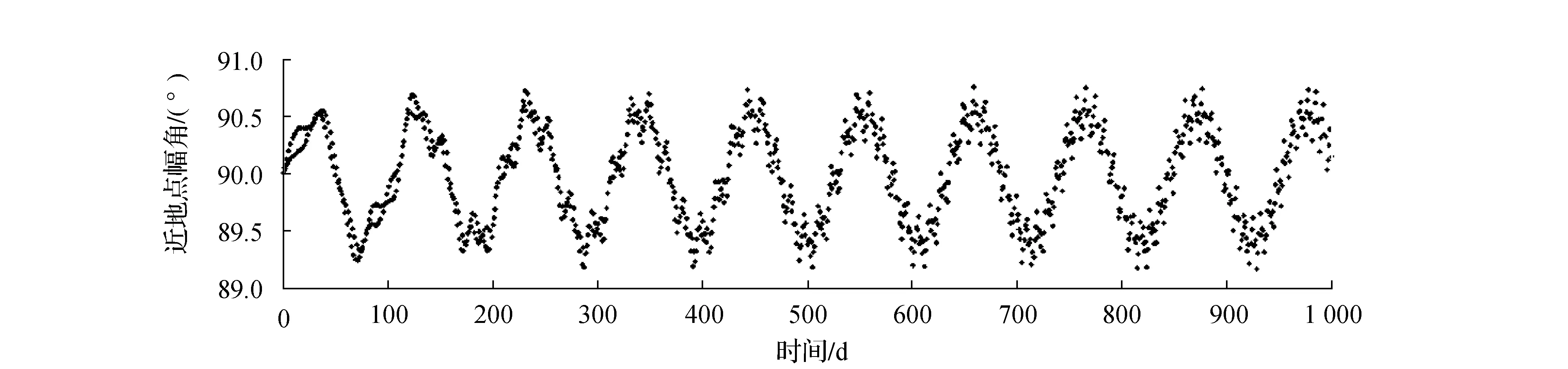
图2 近地点幅角随时间的变化趋势
起始时间给的轨道参数为轨道初始值,在摄动力的作用下轨道发生变化,即反映在参数的变化,由于考虑的摄动力为保守力,并非耗散力,在稳定一段时间之后呈现明显的周期变化。由上面3个图可以看出:偏心率和近地点幅角随时间的变化大致符合正弦曲线;偏心率和近地点幅角的变化都很小(偏心率的变化在5×10-5范围内,近地点幅角的变化在1.5°范围内)。可以得出这组参数满足轨道冻结的条件。
3 结束语
本文分析了非球形引力位中J3项对于卫星轨道的影响。对于地球来说,虽然J3=J2(10-3)量级比较小,但是J3项引起的长周期变化是比较显著的。通过推导,得到了J3项对轨道偏心率以及轨道倾角的影响,介绍了利用它形成冻结轨道的基本原理,并进行了实验验证,实验效果较好(偏心率和近地点幅角的变化都很小),结果表明J3项是冻结轨道形成的重要因素。
[1]陆仲连.地球重力场理论和方法[M].北京:解放军出版社,1996.
[2]周建,吕志伟.地球重力场模型对低轨卫星轨道积分的影响[J].测绘工程,2012,21(2):14-16.
[3]马剑波,刘林,王歆.地球非球形引力位中田谐项摄动的有关问题[J].天文学报,2001,42(11):436-443.
[4]刘林,胡松杰,王歆.航天动力学引论[M].南京:南京大学出版社,2006.
[5]杨威廉.冻结轨道及其应用[J].宇航学报,1990,11(1):23-30.
[6]张玉祥.人造卫星测轨方法[M].北京:国防工业出版社,2007.
[7]杨威廉.基于Brouwer平根数的冻结轨道[J].中国空间科学技术,1998,18(5):22-29.
[8]杨威廉.火星卫星的冻结轨道研究[J].航天器工程,2011,20(3):20-25.
[9]刘林,刘世元,王彦荣.关于大行星(或月球)轨道器的冻结轨道[J].飞行器测控学报,2003,22(2).
[10]陈洁.冻结轨道卫星轨道设计与控制方法研究[D].长沙:国防科学技术大学,2004.
[11]陈洁,汤国建.太阳同步卫星的轨道设计[J].上海航天,2002,19(4):46-50.
[责任编辑:张德福]
TheinfluenceandapplicationoftermJ3innon-sphericalgravitationalpotentialtotheobit
TIAN Jia-lei1,ZHAO Dong-ming1,ZHANG Zhong-kai2,FAN Hao-peng1
(1.School of Geospatial Information,Information Engineering University,Zhengzhou 450052,China;2.School of Navigation and Aerospace Engineering,Information Engineering University,Zhengzhou 450001,China)
The non-spherical gravitational perturbation of the earth plays an important role in the movement of satellites’ circling around the earth.In the research of satellite precision orbit determination and satellite position forecast,J2has been highlighted a lot,yet the termJ3has been neglected.In order to know about the characters ofJ3,its influence on the orbit in non-spherical gravitational potential is analyzed.And the effect on orbital eccentricity and inclination are obtained through rigorous formula derivation.The basic principle of frozen orbit formation is introduced in details as well,as the application verified by numerical experiment.The final results indicate thatJ3is one of the important elements of frozen orbit formation indeed.
termJ3;frozen orbit;non-spherical gravitational perturbation;orbit dynamics
2013-05-31
国家自然科学基金资助项目(41174026;41104047)
田家磊(1988-),男,硕士研究生.
P228
:A
:1006-7949(2014)01-0050-03

