遗传神经网络在大坝安全评价中的应用

张 帆，胡伍生

(东南大学 交通学院，江苏 南京 210096)

遗传神经网络在大坝安全评价中的应用

张 帆，胡伍生

(东南大学 交通学院，江苏 南京 210096)

利用神经网络方法评价大坝安全具有一定的优势，但传统大坝安全评价方法不能为神经网络模型提供合适的学习样本。文中引入安全度值的概念，为神经网络提供可量化的学习样本，并针对BP神经网络收敛速度慢、稳定性差、易陷入局部极小等问题，利用遗传算法进行改进，提出基于遗传神经网络的大坝安全评价方法。工程实例表明，评价方法合理、可行。

大坝安全评价;神经网络;遗传算法;安全度值

大坝安全直接关系到下游人民的生命和财产安全，大坝工作性态的安全监测是及时发现大坝安全隐患的有效手段和途径。及时对大坝安全监测资料进行综合分析，正确掌握和评价大坝的实测性态状况，对于大坝安全十分重要。

大坝安全综合评价是一种多层次、多指标的综合分析体系。安全评判过程中存在着大量的不确定信息[1]，因此从评价指标体系中下一层多个因子的已知状态来评价上一层因子的状态时，需要有经验的专家根据工程实际情况、物理力学关系等，运用其经验、逻辑思维及判断能力，作出合理恰当的评价。目前，国内比较常见的大坝安全评价方法主要包括：层次分析法[2-3]、多级灰关联评估法[4]和模糊综合评判法[5-7]等。此类方法的评价结果往往受评价者主观因素的影响较大，且一旦有新情况就需要重新作出判断。神经网络具有自组织性、自适应性、联想能力及自学习能力，能够吸收学习样本中专家的思维和经验。当利用训练好的网络对新的输入进行映射时，就能在输出的结果中再现专家的思维和经验。吴云芳等[8]将BP神经网络运用于大坝安全评价中，取得了不错的效果。然而，BP神经网络存在收敛速度慢、稳定性差、易陷入局部极小等问题[9]。为此，本文将遗传算法与神经网络相结合，用于大坝安全评价，并根据已有的大坝观测数据验证方法的可靠性。

1 遗传神经网络原理

1.1 遗传算法基本原理

遗传算法是一种借鉴生物界自然选择和自然遗传机制的高度并行、随机、自适应搜索算法，具有全局收敛性和初值无关性[10]。它不要求目标函数连续、可微，仅需给出目标函数的描述，从一组随机产生的初始解开始，从全局空间出发搜索问题的最优解。遗传算法的基本操作如下：

1)编码：由于遗传算法不能直接处理解空间的解数据，因此必须通过编码将它表示成遗传空间的基因型串结构数据——染色体。

2)初始群体的生成：由于遗传算法的群体型操作需要，必须为遗传操作准备一个由若干初始解组成的初始群体，然后以这个初始群体作为起始点开始迭代搜索。

3)定义适应度函数：遗传算法在搜索进化过程中一般不需要其它外部信息，仅用适应度函数值来评估个体或解的优劣，并作为遗传操作的依据。

4)选择：选择操作的目的是为了从当前群体中选出生命力强的染色体，使它有机会保留并用以繁殖后代。选择操作体现了达尔文的优胜劣汰、适者生存的原则，个体适应度越大，其被选择的机会就越多。

5)交叉：交叉操作是遗传算法中最主要的遗传操作，对于用于繁殖后代的个体，随机选择交叉位置，产生两个新的个体，这两个新个体组合其父代的特性。

6)变异：变异操作在群体中随机地选择一个个体，以一定的概率随机改变基因串中某个字符的值。它需要和交叉操作配合使用，目的是挖掘群体中个体的多样性，克服有可能局限于局部最优解的弊端。

1.2 遗传算法用于优化神经网络权重

遗传算法与BP神经网络的结合有多种方式，本文利用遗传算法来优化神经网络的连接权值，具体过程为：首先利用神经网络的连接权重作为染色体进行编码，形成初始种群，然后以适应度函数指导随机搜索的方向，对父代种群进行选择、交叉、变异等操作生成子代种群。经过不断迭代计算，最终产生全局最优解，并对其解码作为BP网络的最优初始权值。

利用改进的BP神经网络，即遗传神经网络进行样本学习，可在相当大的程度上避免局部极小，训练次数和最终权值也可以相对稳定，同时加快训练速度。近年来，已有众多学者将遗传神经网络应用于工程实践[11-12]，本文利用MATLAB编制遗传神经网络程序并应用于大坝安全评价。

2 基于遗传神经网络的大坝安全评价

传统的大坝安全评价是一个极其复杂的过程，需要专家经验的介入。如果能建立一个特殊模型，通过输入原始观测数据即能输出大坝安全评价结果，将节省大量人力物力，而遗传神经网络凭借其自身优势，为建立这样的模型提供了可能。然而，传统的大坝安全评价方法不能为神经网络模型提供合适的学习样本，因此本文引入安全度值的概念，使学习样本得到量化，即：首先计算每个底层指标因子的安全度值，再判断每个下层指标因子相对于其上层指标因子安全程度的权重，两者结合逐级递归综合评价，最终得到大坝整体结构的安全度值，并作为样本进行建模。整个过程主要解决3个问题，即如何计算底层指标因子的安全度值、如何计算权重、如何利用遗传神经网络建模。

2.1 底层指标因子安全度值计算

所谓安全度值，即大坝整体及各因子安全程度的数值体现。何金平等[13]从相应规范、已有方法、人类心理活动以及实践经验角度出发，提出将大坝结构实测性态综合评价的安全级数确定为5级，即正常、基本正常、轻度异常、重度异常和恶性失常。令安全度值为(0～1]区间上，并将其等分成A到E 5个区间，与5种安全状态一一对应，其结果如表1所示。

表1 评价等级安全度值对照表

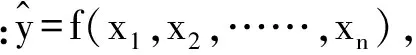
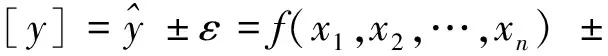
(1)

(2)

式中：n为模型中实测效应量总数；k为实测效应量的自由度。则式(1)可表示为

[y]=f(x1,x2,…,xn)±pS.

(3)

安全度值的等级区间同样可以用监控指标来表示，使人为划定的等级区间和通过统计模型回归分析所得的监控指标相挂钩：

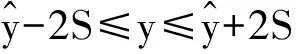
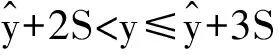
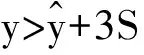
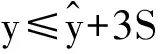
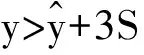
(4)

式中：ymax，ymin为监控指标的限制值。根据表1及式(4)，即可推导得到各底层指标因子安全度值的计算公式，结果见表2，表中各符号含义同上。

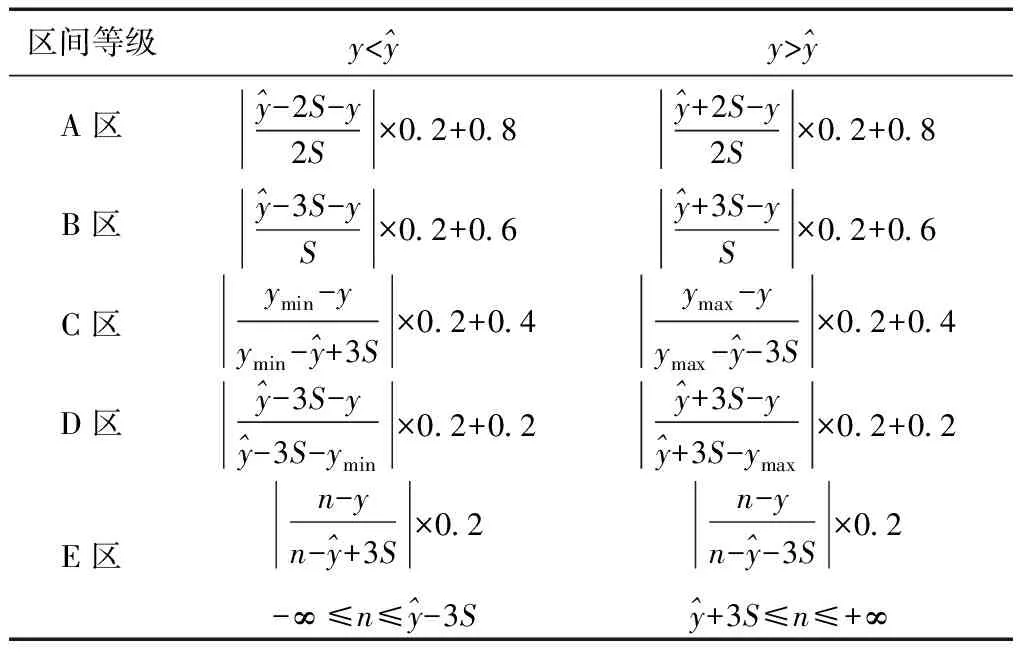
表2 底层指标因子安全度值计算公式

2.2 权重计算

计算得到大坝底层指标因子安全度值以后，不能通过简单的加减就得出上一层指标因子的安全度值，必须把每个指标因子相对于其上一级指标因子的权重计算出来，并进行综合计算得出。本文将利用主成分分析法计算底层指标因子的权重，利用改进的层次分析法计算其余各级指标因子的权重。

2.2.1 主成分分析法

在大坝安全评价中，主成分分析法直接依据大坝原始实测资料的信息建立监测样本相关矩阵，然后通过正交变换，把多个相关指标转化为少量不相关评价指标[14]，并定量描述交互指标在整体系统中贡献，并通过贡献量大小来识别对应的各个评价指标的权重值。

2.2.2 改进的层次分析法

层次分析法的基本思路是：专家通过对评价因素重要程度的两两比较，确定判断矩阵，然后计算判断矩阵的最大特征值及其对应的特征向量，再将该特征向量归一化并得到评价因素的权重。然而不论是传统的层次分析法常用的A.L.Satty的1～9标度法，还是一些学者后来相继提出的9/9～9/1标度法、10/10～18/2标度法以及指数标度法，在实际应用中都并不合理。为此，本文采用一种改进的层次分析法。

在大坝安全评价中，考虑到评价因素两两比较时一般不存在“强烈大”和“极端大”的情况，出现“明显大”的情况也不多。因此，在对指标重要性两两比较时，只设置两个等级，即重要性“相同”或“稍微大”，然后以此作为基础递进乘积分析。本文取9/9～9/1标度法、10/10～18/2标度法以及指数标度法三者的平均值作为标度，即“相同”的标度取为(1+1+1)/3=1，“稍微大”的标度取为(1.286+1.500+1.277)/3=1.354。当评价指标之间的重要性用“稍微大”还不足以反映时，可以用多个“稍微大”来反映，标度为1.354×1.354=1.833，以此类推并最终计算出各评价指标权重。

2.3 遗传神经网络建模

根据底层指标因子安全度值及各级因子间的权重，就可以计算得到大坝整体结构安全度值，从而进行神经网络建模。本文中，遗传神经网络的输入层为大坝安全观测的各项原始观测数据，输出层为大坝整体结构安全度值。

利用生成的学习样本训练网络，就能使网络获取客观模型分析结果和主观专家评价经验，当应用这一网络对新的输入进行映射时，就可在输出的评价结果中再现主客观相结合的评价思维，从而得出比较合理的评价结论。因此当网络训练完成后，在输入层中依次输入各项原始观测数据，即可得到最终的大坝结构安全度值。

3 工程实例分析

3.1 工程概况及建模数据选取

陈村水电站位于皖南长江支流青弋江上游，是一座综合性中型水利水电枢纽工程。大坝是一座同心圆变半径的混凝土重力拱坝，坝顶高程为126.3 m，最大坝高为76.3 m，坝顶弧长419 m，坝顶宽8 m，最大坝底宽53.5 m，自左向右有28个坝段，总库容为28.25亿m3。

本文仅考虑变形因素的影响，选取6个典型坝段，即5#、7#、8#、18#、24#、26#坝段，基于遗传神经网络进行大坝安全评价，资料系列选取该坝1999—2006年间的垂直位移、径向水平位移和切向水平位移的观测数据。

3.2 学习样本生成

利用1999—2004年的数据分别建立各单测点垂直位移、径向水平位移及切向水平位移的统计模型，对2005—2006年的84组样本进行拟合，再根据表2中算式计算84组样本的底层指标因子安全度值，并利用主成分分析法确定底层因子的权重。现以2006年2月4日为例，具体计算结果见表3。

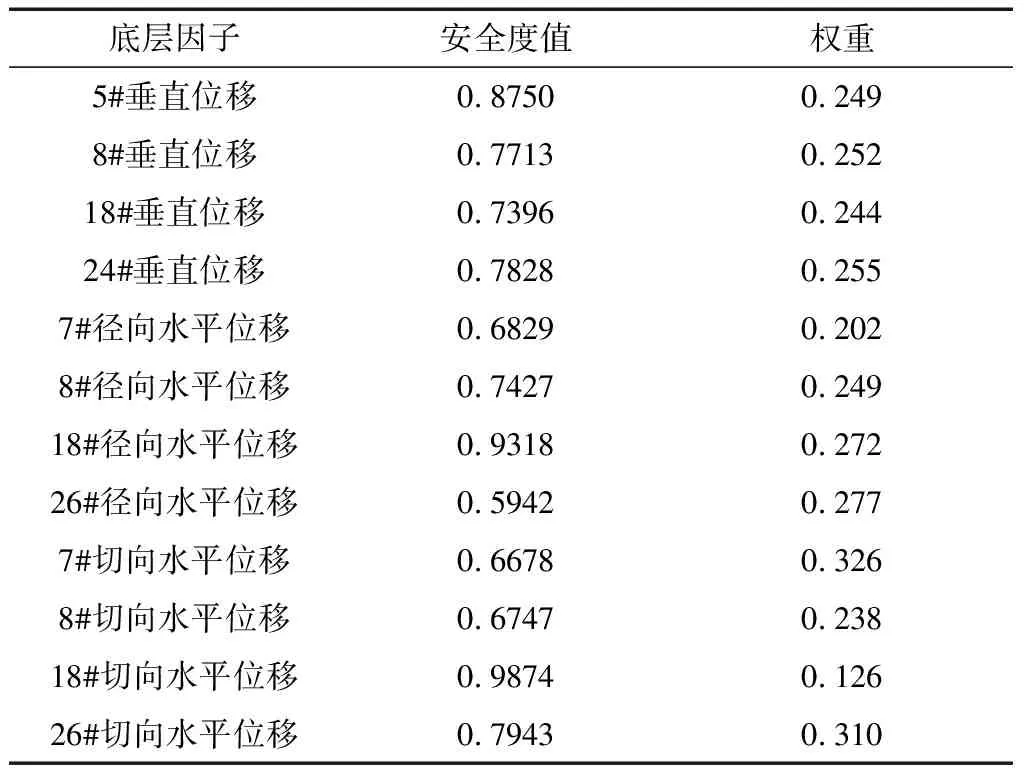
表3 底层指标因子安全度值及权重

根据表3，可以分别算出2006年2月4日垂直位移、径向水平位移和切向水平位移因子的安全度值，再利用改进的层次分析法可以算出各因子的权重，具体计算结果见表4。

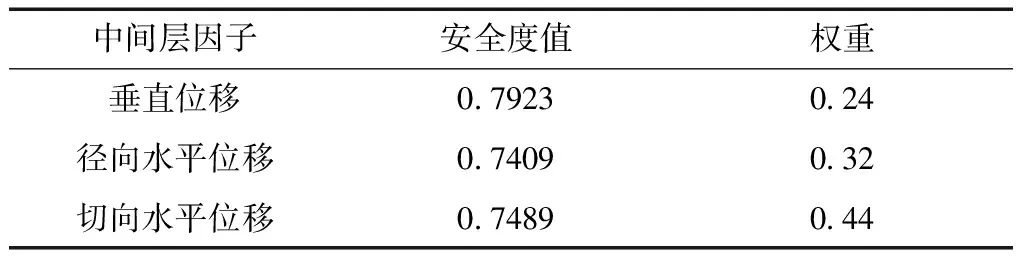
表4 中间层因子安全度值及权重

根据表4计算可得2006年2月4日大坝整体变形的安全度值为0.756 8，同理可得其余83个时间点的大坝整体变形安全度值，其范围在0.688 1～0.843 0之间，均处于基本正常或者正常状态。而陈村大坝已运行30余年，工作状态基本正常，计算结果与大坝实际检测结果相符，可以作为样本用于神经网络建模。

3.3 神经网络建模

利用遗传神经网络进行建模，输入层为12个位移原始观测数据，输出层为大坝整体变形的安全度值。将2005—2006年84组数据中的50%作为学习样本，另50%作为预报样本，开始训练。训练结束后，得到42个预报样本的模拟结果，具体结果见图1、表5。

由表5可知，遗传神经网络的拟合结果与实际结果相比，差值绝对值最小仅为0.000 7，差值绝对值最大也只有0.040 3，拟合效果良好，方法具有一定的可行性。

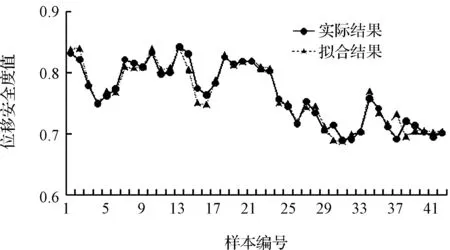
图1 拟合结果与实际结果对比

4 结束语

本文在已有方法的基础上，建立大坝安全评价的遗传神经网络模型，解决传统BP神经网络收敛速度慢、稳定性差、易陷入局部极小等问题。通过引入安全度值的概念将网络学习样本量化，并在学习过程中融合相关专家的经验、知识、主观判断及对目标重要性的倾向。网络训练完成后，可直接通过原始大坝观测数据进行大坝安全评价。

[1]张乾飞,王锦国,李雪红. 大坝安全监控中的不确定性信息初探[J]. 河海大学学报:自然科学版, 2002，30(5):113-117.

[2]季根蔡. 基于层次分析法的水库大坝安全鉴定的综合评价[J]. 红水河，2007，26(1):133-136.

[3]陈诚,花剑岚. 改进层次分析法在土石坝安全评价中的应用[J]. 水利水电科技进展，2010，30(2):58-62.

[4]吴云芳,李珍照,薛桂玉. 大坝实测性态的多级灰关联评估方法研究[J]. 大坝观测与土工测试，1998，22(5):27-31.

[5]李珍照,何金平,薛桂玉,等. 大坝实测性态模糊模式识别方法的研究[J]. 武汉水利电力大学学报，1998，31(2):1-4.

[6]张小飞,苏国韶,吴彰敦. 基于层次模糊综合评价的水库大坝安全评价法[J]. 广西大学学报:自然科学版，2009，34(3):321-325.

[7]姜彤,杜国倩. 模糊评判法在大坝安全评价中的应用[J]. 人民黄河，2012，34(3):117-119.

[8]吴云芳,李珍照,徐帆. BP神经网络在大坝安全综合评价中的应用[J]. 河海大学学报:自然科学版，2003，31(1):25-28.

[9]胡伍生. 神经网络理论及其工程应用[M]. 北京：测绘出版社, 2006:68-69.

[10]杨发群,邱卫宁,魏成,等. 顾及不确定因素的GA-BP神经网络在路基沉降预测中的应用[J]. 测绘工程，2013，22(6):51-54.

[11]刘健,蔡建军,程森. 基于遗传神经网络的大坝变形预测模型研究[J]. 山东大学学报:工学版,2006，36(2):62-66.

[12]王志军,刘红彩. 遗传神经网络在大坝变形预报因子重要度判定中的应用[J]. 水电自动化与大坝监测，2008，32(5):69-71,75.

[13]何金平,李珍照. 大坝结构实测性态综合评价指标体系的研究[J]. 大坝观测与土木测试，2000，24(6):20-22.

[14]韩小孩,张耀辉,孙福军,等. 基于主成分分析的指标权重确定方法[J]. 四川兵工学报，2012，33(10):124-126.

[责任编辑：张德福]

Application of genetic neural network to dam safety evaluation

ZHANG Fan, HU Wu-sheng

(Dept. of Surveying Engineering, Southeast University, Nanjing 210096, China)

Application of neural network to the dam safety evaluation has some advantages, but the traditional methods of dam safety evaluation can not provide the appropriate learning samples for the neural network model. The concept of safety degree value is introduced to provide quantifiable learning samples for neural network. And aiming at the problems of slow convergent rate, poor stability and local minimum of the BP neural network, an improved dam safety evaluation method based on genetic neural network is proposed. The example shows that the method is reasonable and feasible.

dam safety evaluation; neural network; genetic algorithm; safety degree value

2014-02-25

江苏省普通高校研究生科研创新计划项目(CXLX11_0143)

张 帆(1987-)，男，博士研究生.

TU196

：A

：1006-7949(2014)07-0041-05