基于八节点二次壳单元的等效结构应力法

, ,效贵

(浙江工业大学 机械工程学院，浙江 杭州 310014)

焊接是常见的结构连接方式，广泛应用于车辆工程、航天航空、海洋与船舶工程以及机械工程等众多领域.焊接接头是焊接结构中最容易发生疲劳失效的部位，原因在于该部位存在较大的应力集中，并常伴有残余拉应力和各种焊接缺陷.焊接接头的疲劳强度将直接决定整个焊接结构的使用是否安全，因此对焊接接头进行疲劳强度分析十分必要.

传统焊接接头疲劳评估方法各有其局限性[1-2]：名义应力法依赖于焊接接头形式和载荷类型，对于实际复杂的焊接接头会出现无法归类的问题；局部应力法解决了名义应力法的局限性，但焊缝的局部参数如焊趾半径、焊趾倾角具有随机性，无法有效应用于实际的焊接结构；热点应力法对网格尺寸和网格划分方式有严格的要求，难以准确预测焊缝处的疲劳寿命.Dong及其合作者[3-6]提出了一种预测焊接结构疲劳寿命的等效结构应力法，该方法首先将有限元计算得到的焊趾处的节点力转化为分布线力，然后基于结构力学基本原理由线力计算结构应力，进而在断裂力学框架内给出了考虑焊趾缺口、板厚尺寸和加载模式等因素影响的等效结构应力转化方程，最后基于主S-N曲线和等效结构应力即可预测焊趾疲劳寿命.等效结构应力法对网格尺寸和单元类型均不敏感，预测的疲劳寿命和失效位置与试验结果有很好的一致性，具有广阔的工程应用前景，且已被ASME VIII Division 2—2010标准采用[7-9].前述文献集中于研究四节点线性壳单元和三维实体单元，尚未见关于八节点二次壳单元的系统研究工作.笔者首先导出了八节点二次壳单元的节点力与分布线力的关系式，然后基于结构力学基本原理给出了由线力和线力矩表示的结构应力表达式.然后，利用T型焊接接头考核基于二次壳单元结构应力的有效性，并验证了单元类型与网格尺寸的不敏感性.最后，对RHS管接头的疲劳失效位置与疲劳寿命进行了预测，数值结果与实验测试数据基本吻合.

1 基于二次壳单元的等效结构应力法

基于结构力学基本理论，结构应力σs由膜应力σm和弯曲应力σb两部分组成[3].对于壳单元，基于图1所示的局部坐标系x′y′z′，焊趾截面A-A上的结构应力可表示为

(1)

式中：δ为焊趾截面A-A与参考面B-B的距离；fx′和fz′为参考面B-B上的分布线力；my′为参考面B-B上的分布线力矩;t为壳单元的厚度.当参考面B-B与焊趾截面A-A重合时，式(1)可简化为

(2)

结构应力集中系数Ks为

Ks=σs/σn

(3)

式中σn为垂直于A-A截面的名义正应力.

采用八节点二次壳单元分析焊接接头，某代表性焊趾壳单元如图2所示.以C为原点，AB边为自然坐标轴，则点A，C，B的形函数可由自然坐标ξ表示为

(4)

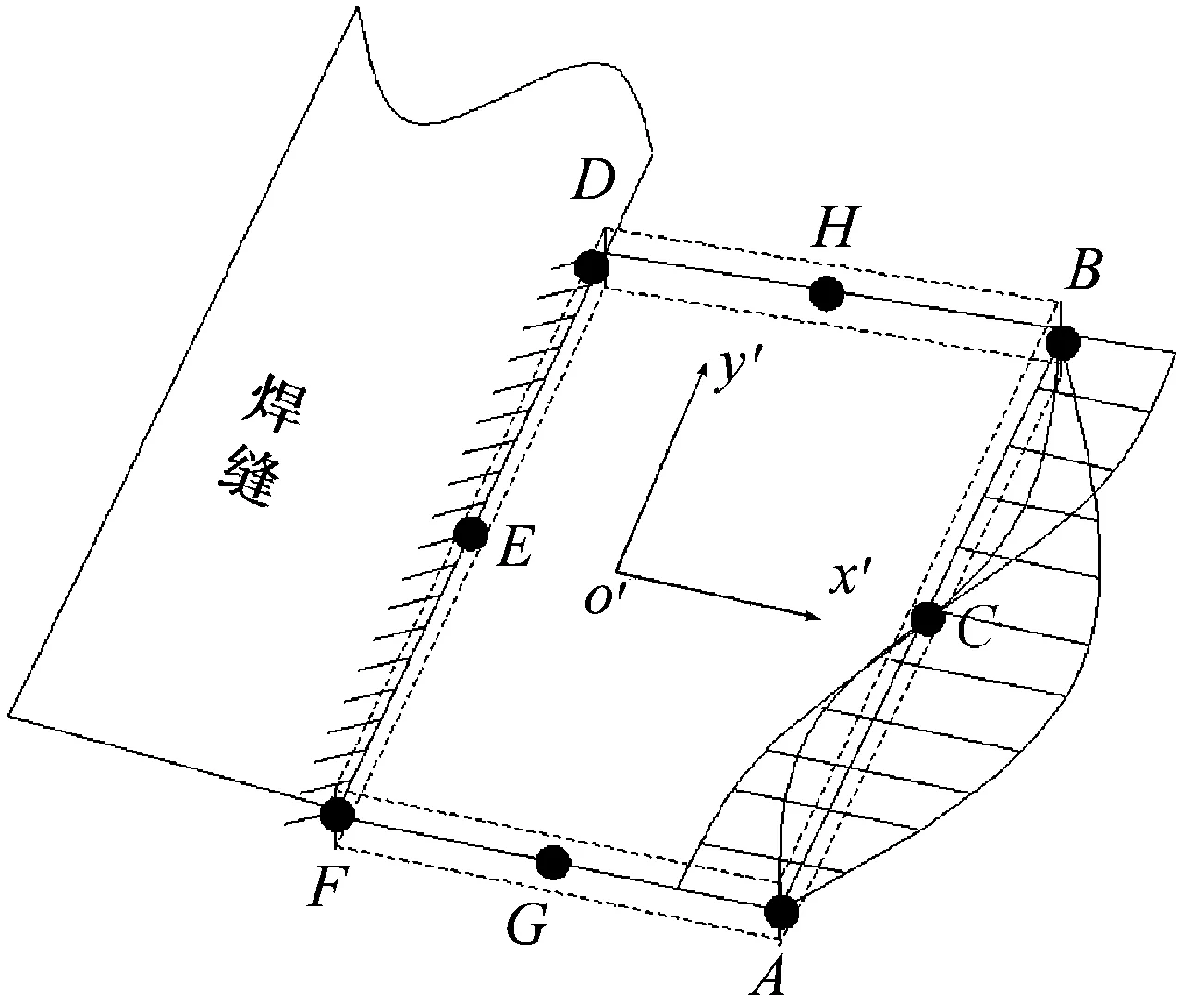
图2 线力分布示意图

焊趾截面AB上任意点的局部y′坐标，可表示为

(5)

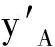
f(ξ)=NAfA+NCfC+NBfB

(6)

式中：fA，fC，fB分别为节点A，C，B上的线力或线力矩.计算结构应力所需的分布线力和分布线力矩，可基于功等效原理由节点力和节点力矩导出，即

(7)

式中：FA，FC，FB分别为局部坐标系o′x′y′下节点A，C，B上的单元节点力或节点力矩.将式(4)代入式(7)，化简后得

(8)

式中lAB为焊趾单元沿焊缝方向的长度.式(8)与ASME VIII Division 2-2010标准[10]中给出的单元节点力与线力的关系式具有相同的形式.

一般情况下，连续焊缝的焊趾可划分为n个二次壳单元，如图3所示.对于非闭合焊缝，有2n+1个焊趾节点.将单元节点力或节点力矩集成，可得

(9)

对于闭合焊缝，则有2n个焊趾节点.将单元节点力或节点力矩集成，可得

(10)

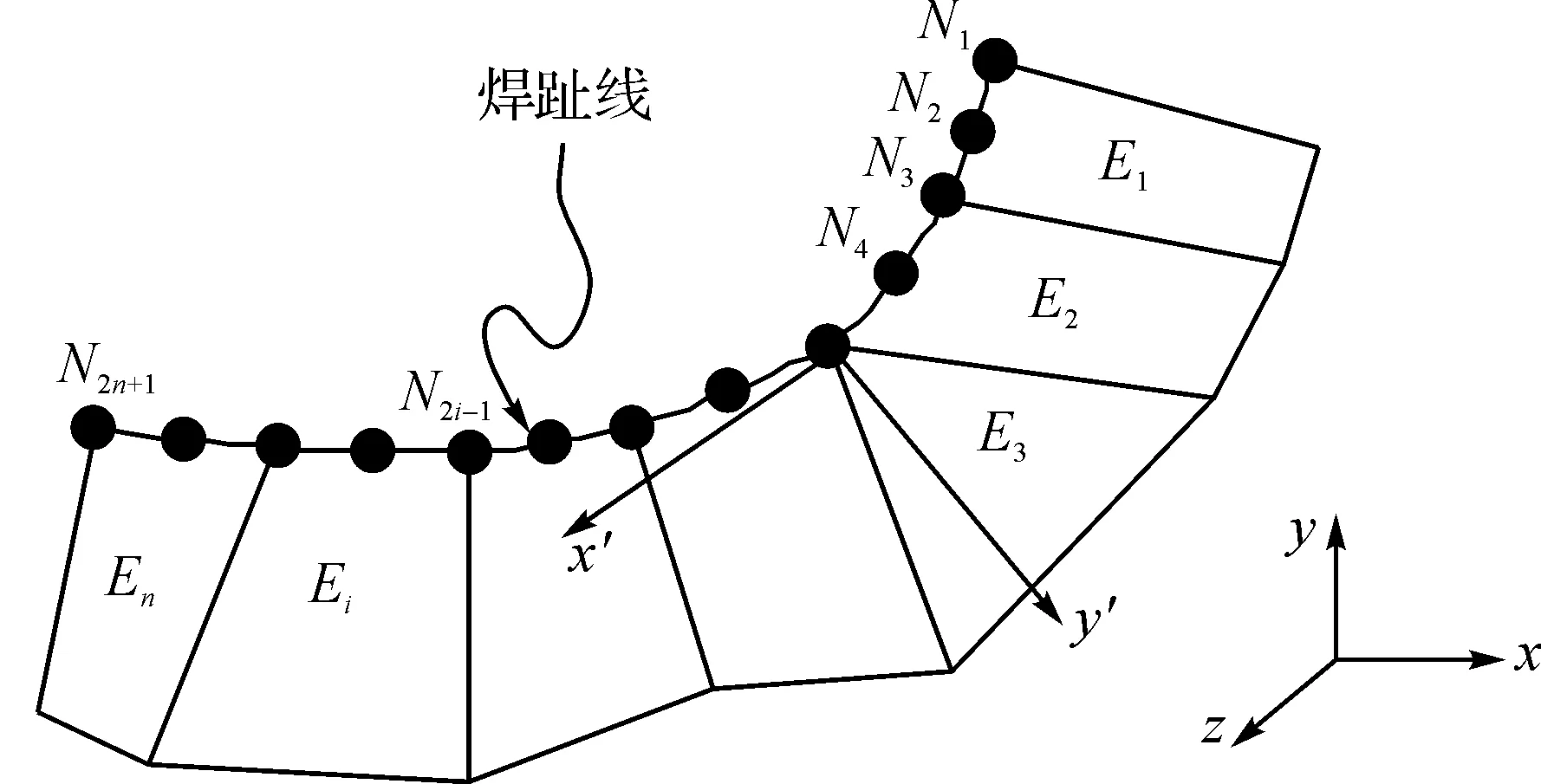
图3 焊趾二次壳单元的剖分示意图

基于壳单元有限元分析结果，计算结构应力的步骤：通过有限元计算得到整体坐标系下焊趾处的节点力，经过坐标转换得到局部坐标系下的节点力，然后通过式(9)或式(10)求出分布线力和分布线力矩，代入式(2)后求出结构应力.

Hiroko和Dong[4]以结构应力为控制参数计算应力强度因子，在考虑焊趾缺口、板厚尺寸和加载模式等影响因素的基础上，基于断裂力学分析确定与疲劳寿命直接相关的应力参数，最终导出的等效结构应力为

(11)

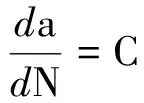
lgN=12.185 448-3.055 953lgΔSs

(12)

2 结构应力的计算

2.1 T型接头

图4为T型焊接接头受力分析模型.水平放置母板的厚度为t，长度为40t，宽度为5t.竖直放置附板的厚度为t，高度为7t，宽度为5t.焊缝倾角为45°，焊脚长度均为t.水平母板的左端固定，右端面施加均布拉力，并且限制右端面附近区域沿板厚方向的线位移；竖直附板的上端面固定.母板与附板的弹性模量均为210 GPa，泊松比为0.3.

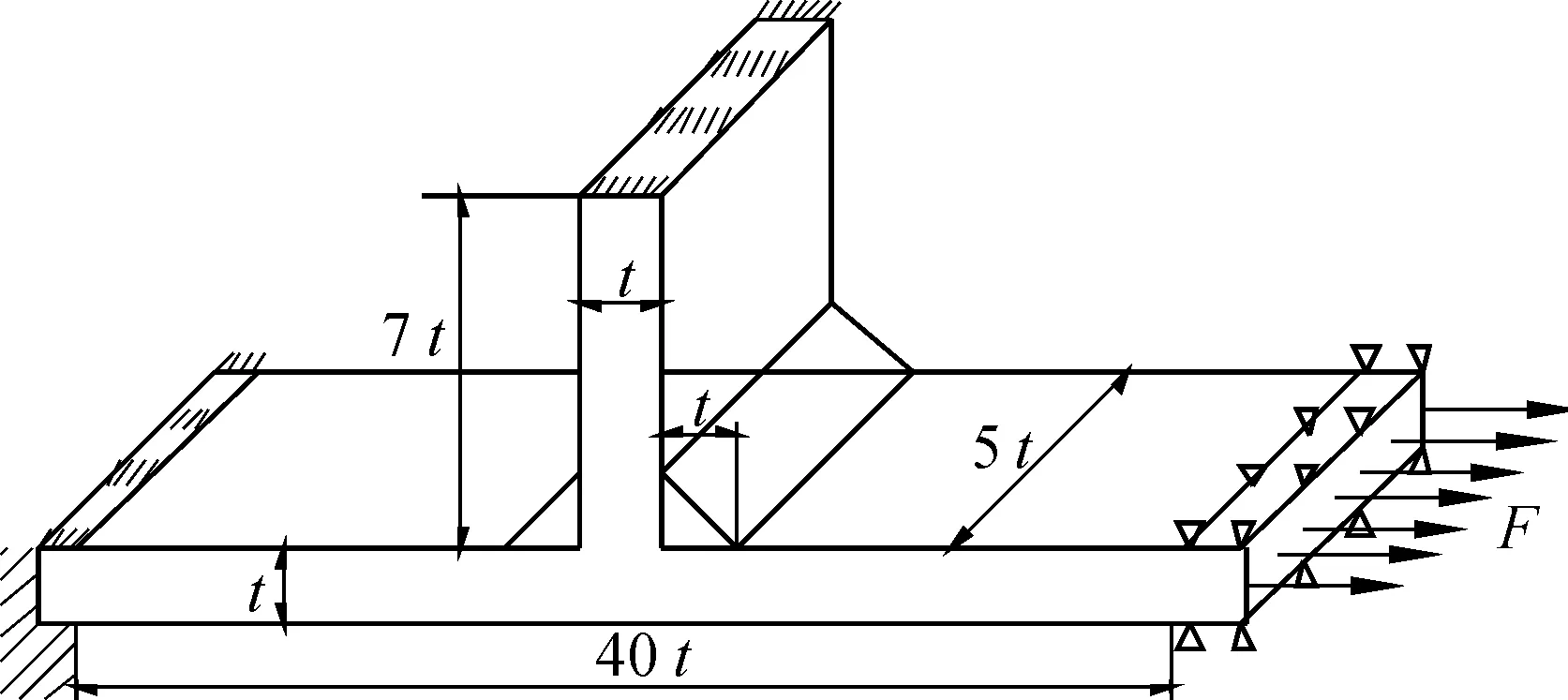
图4 T型焊接接头的受力分析模型

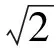
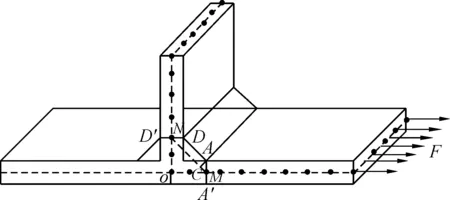
图5 T型焊接接头的壳单元建模示意图

为了考察单元类型对焊趾处结构应力集中系数的影响，采用了线性壳单元(S4R)和二次壳单元(S8R)；为了考虑单元大小对焊趾处结构应力集中系数的影响，针对两种壳单元分别划分了边长为0.25t×0.25t，1.00t×1.00t，1.67t×2.06t的四边形焊趾单元网格.

对于S8R有限元模型，基于从结果ODB文件中提取的焊趾单元节点力和节点力矩计算结构应力；对于S4R有限元模型，则由文献[3]中的方法求解结构应力.然后，把结构应力与名义应力代入式(3)，即可求出T型焊接接头的焊趾结构应力集中系数，结果如图6所示.显然，无论是S4R壳单元还是S8R壳单元，三种不同尺寸的有限元网格得到的结构应力集中系数基本一致，不但说明结构应力对单元类型和网格尺寸都不敏感，而且验证了基于二次壳单元的结构应力计算公式的有效性.

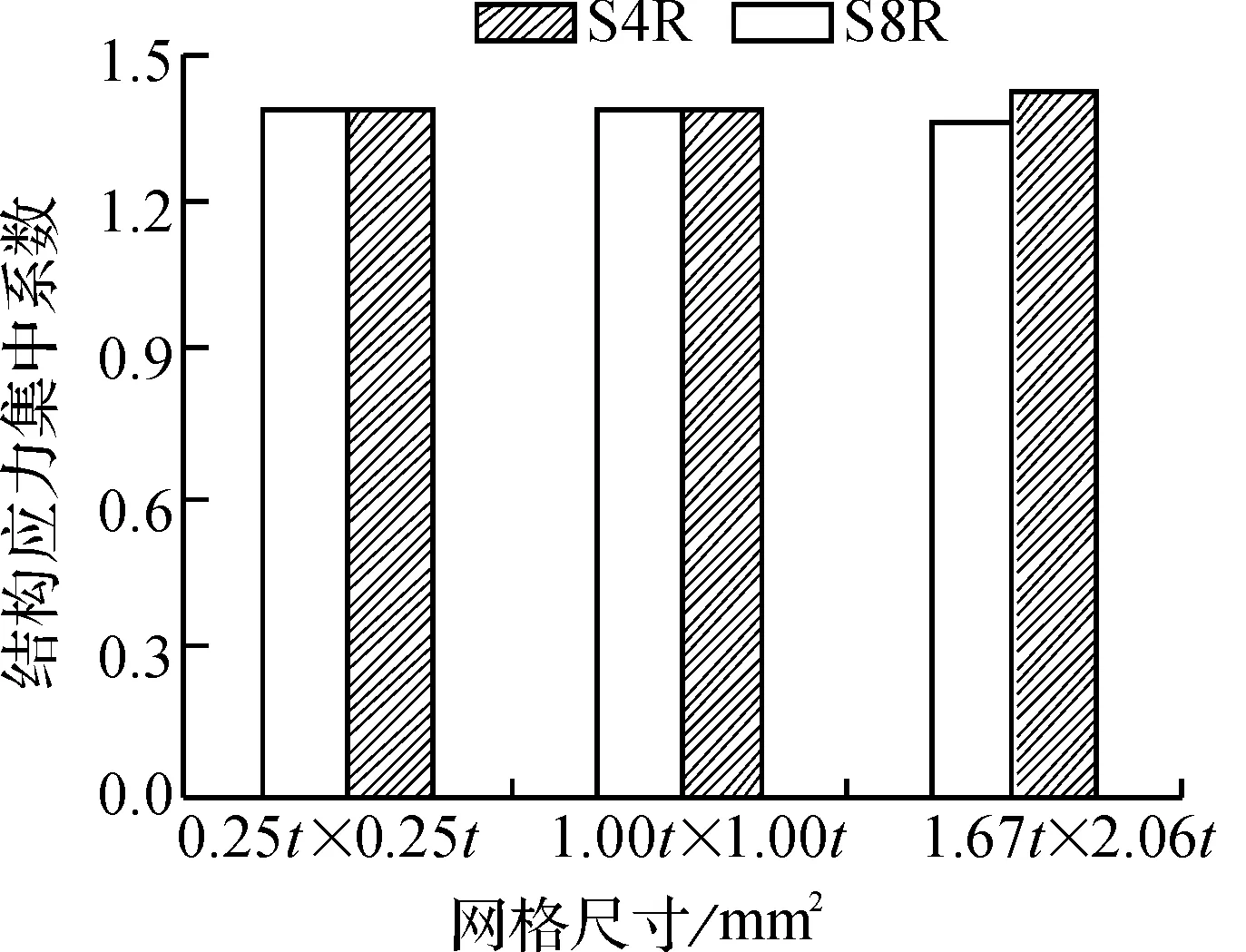
图6 T型接头焊趾的结构应力集中系数

2.2 方形空心截面管接头

SAE FD&E委员会于2003年公布了方形空心截面(RHS)管焊接接头模型[4].RHS接头由101.6 mm×101.6 mm和50.8 mm×152 mm方形截面空心管焊接而成，管长分别为600 mm和364 mm，空心管的壁厚t为7.9 mm.焊缝为T型单边焊，焊缝倾角为45°，焊脚长度为t.材料的弹性模量为210 GPa，泊松比为0.3.

基于T型焊接接头的壳单元建模方法(图5)，建立如图7所示的RHS接头的有限元分析模型.把正方形截面管左端通过MPC Beam命令刚性耦合到截面的中心点，在中心点正上方317.5 mm处定义一个参考点，并将中心点与参考点刚性耦合，RHS接头的另外两端固定，在参考点上沿x方向施加17.8 kN的对称交变载荷.T型焊接接头的分析已经验证了焊趾结构应力的网格不敏感性，因此仅用大小为t的S8R壳单元对RHS接头进行网格划分.

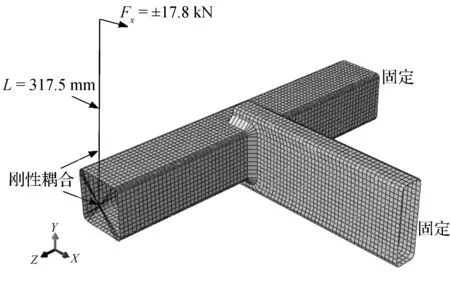
图7 RHS管接头的有限元分析模型

由于是对称循环加载和线弹性分析，Fx=17.8 kN和Fx=-17.8 kN作用下同一焊趾截面的结构应力绝对值相等.当Fx=17.8 kN时，提取ODB结果中焊趾单元的节点力和节点力矩，由其求出的结构应力分布如图8(a)所示，虚线所示焊趾位于101.6 mm×101.6 mm截面上(记为焊趾A)，实线所示焊趾位于50.8 mm×152.4 mm截面上(记为焊趾B).对比沿焊趾A和焊趾B的结构应力分布可见：结构应力最大值出现在焊趾B的圆弧拐角处.拐角处沿焊趾A的结构应力分布的局部放大图见8(b)，三角形符号代表划分5 个壳单元时的结果，而实线对应于90个壳单元的情况.由于焊趾在圆弧拐角处的曲率较大，相邻壳单元法向的夹角也相应较大，导致中间节点处的结构应力相对于角节点出现明显波动，显然该问题可通过在该处采用较细的网格划分得以解决.

图8 焊趾的结构应力分布

结构应力范围为Fx=17.8 kN时求得结构应力的两倍，即Δσs=2σs.把Δσs代入式(11)，可求出等效结构应力范围ΔSs.把ΔSs代入式(12)，则可得到存活率为50%时的焊趾疲劳寿命.由于Δσs和ΔSs满足线性关系，显然由ΔSs预测的危险截面与Δσs的预测结果完全一致，也就是说疲劳失效位置为焊趾B的圆弧拐角处，疲劳寿命为8.2×104个加载循环.

RHS管接头的疲劳寿命试验共测试了12个试样，疲劳寿命的最大值、最小值和平均值分别为2.0×105，3.0×104，7.5×104，疲劳失效位置都发生在图8所示的焊趾B的圆弧拐角处[4].由上述分析可知：等效结构应力法预测的疲劳失效位置与试验结果完全一致，存活率为50%时的疲劳寿命预测值介于试验结果的最大值与最小值之间，且与平均值非常接近.

3 结 论

首先导出了基于八节点二次壳单元的分布线力与分布线力矩，然后基于结构力学基本理论得到了焊趾截面上的结构应力表达式.通过T型焊接接头的分析，验证了基于八节点二次壳单元的结构应力计算公式的有效性，而且发现单元类型与网格尺寸对结构应力影响极小.对RHS管接头的研究表明：基于八节点二次壳单元的等效结构应力法可以准确地预测焊趾的疲劳失效位置与疲劳寿命.

参考文献：

[1] 袁熙，李舜酩．疲劳寿命预测方法的研究与现状[J]．航空制造技术，2005(12)：80-84．

[2] 周张义，李芇，黄运华．基于热点应力的焊缝疲劳强度评定研究[J]．内燃机车，2008(7)：1-10．

[3] DONG P． A structural stress definition and numerical implementation for fatigue analysis of welded joints[J]．International Journal of Fatigue，2001，26：865-876．

[4] HIROKO K， DONG P． Equilibrium-equivalent structural stress approach to fatigue analysis of a rectangular hollow section joint[J]．International Journal of Fatigue，2005，27：85-94．

[5] DONG P， HONG J K． The master S-N curve approach to fatigue evaluation of offshore and marine structures[C]．Vancouver：The American Society of Mechanical Engineers，2004：1-9．

[6] DONG P， HONG J K， CAO Z． Stresses and stress intensities at notches：“anomalous crack growth” revisited[J]．International Journal of Fatigue，2003，25(9/10/11)：811-825．

[7] DONG P， HONG J K， DE-JESUS A M P． Analysis of recent fatigue data using the structural stress procedure in ASME Div 2 Rewrite[J]．Journal of Pressure Vessel Technology，2007，129：355-362．

[8] ASME Boiler and Pressure Vessel Committee on Pressure Vessels．ASME VIII division 2—2010 ASME boiler and pressure vessel code[S]．New York：The American Society of Mechanical Engineers，2010．

[9] 武奇，邱慧清，郑洋．基于壳单元的焊接接头的结构应力求解[J]．焊接学报，2010，31(7)：22-26．