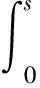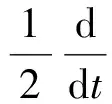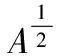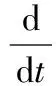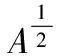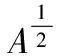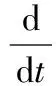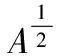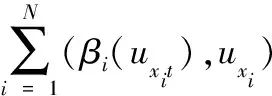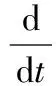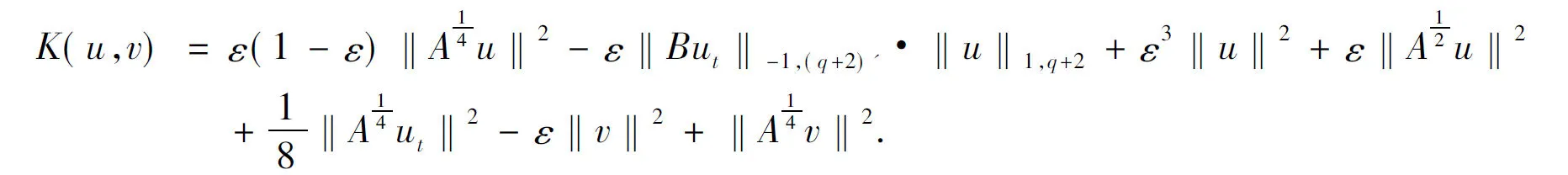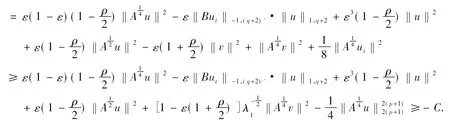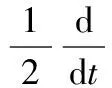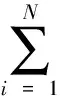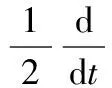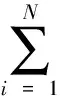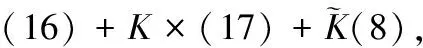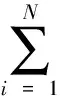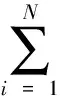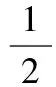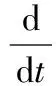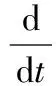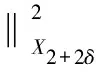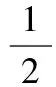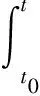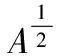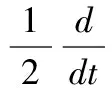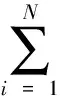一类四阶非线性发展方程整体解的存在唯一性
张媛媛, 王宏伟
(1.开封大学 数学教研部,河南 开封 475000;2.安阳师范学院 数学与统计学院,河南 安阳 455000)
一类四阶非线性发展方程整体解的存在唯一性
张媛媛1, 王宏伟2
(1.开封大学 数学教研部,河南 开封 475000;2.安阳师范学院 数学与统计学院,河南 安阳 455000)
研究一类四阶非线性发展方程整体解的存在唯一性,借助偏微分方程的一些标准技巧对非线性项进行估计,利用嵌入定理和算子半群的方法证明了在相对较弱的条件下上述问题整体解的存在唯一性.
整体解;存在性;唯一性
1 预备知识
具耗散项非线性发展方程的整体解是近年来偏微分方程研究的热点,目前关于它的研究主要集中在其存在性和惟一性方面.本文的目的是研究下列一类四阶具耗散项方程
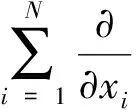
(1)
u|∂Ω=0,t>0,
(2)
u(x,0)=u0(x),ut(x,0)=u1(x),x∈Ω.
(3)
(Ω是RN中具有光滑边界的有界区域)整体解的存在唯一性.方程(1)有一定的物理模型,它主要描述的是一类具黏弹性材料的振动[1-4],此类方程也频繁出现在具黏弹性构形且服从Voight非线性模型的纵向运动中[5].考虑到偏微分方程和无穷维动力系统的密切关系,因此笔者尝试用算子半群的方法探讨该问题的整体解,最终得到在相对较弱的条件下整体解的存在性和唯一性.
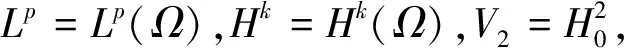
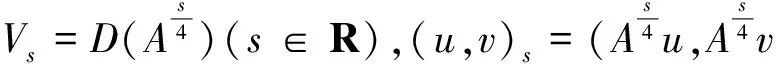
(4)
u(x,0)=u0(x),ut(x,0)=u1(x).
(5)
引理1[6]设X,Y是Banach空间,并且X⊂Y.若φ∈L∞(0,T;X)ICw([0,T];Y),则
φ∈Cw([0,T];X).
引理2[7](Aubin-Lions) 设B0,B和B1是Banach空间,且B0⊂⊂B⊂B1,B0,B1是自反的.W={v|v∈Lp0(0,T;B0),vt∈Lp1(0,T;B1)},这里0 引理3[7]设z(t)非负,是[0,∞)上的绝对连续函数,满足下列不等式 定理假定下列条件成立 (ii)βi∈C1(R),βi(s)s≥B3|s|q+2,|βi(s)|≤B4(1+|s|q+1); (iii)(u0,u1)∈X2+2δ. 证明:(4)式与ut作内积,得: (6) (7) (8) (8)式积分,并结合(7)式,得: ≤C(‖(u0,u1)‖X2,T),t∈[0,T]. (9) 设v=u1+εu,则v满足 (10) (10)式与v作内积,得: (11) (12) 将上式代入(11)式,得: (13) 通过计算,得: K(u,v)-ερH(u,v) 将上式代入(13)式,得: (14) 由(12),(14)式并利用引理3,得: (15) 设R>0,对于给定的(u0,u1)∈X2+2δ且‖(u0,u1)‖X2+2δ≤R,则‖(u0,u1)‖X2≤R. (16) (17) (18) (19) (20) (21) 将(19)-(21)式代入(18)式,得: (22) (23) 由(4),(22),(23)式和假定,得: ‖utt‖L2(0,T;V2δ-1)≤‖u‖L2(0,T;V1+2δ)+‖ut‖L2(0,T;V1+2δ)+‖u‖L2(0,T;V3+2δ) ≤C(R)(‖u‖L2(0,T;V3+2δ)+‖ut‖L2(0,T;V1+2δ)+1)≤C(R,T), t∈[0,T]. (24) t>0,j=1,2,…,n, (25) 显然,估计(22)-(23)式对un仍成立.因此,可从中抽取子序列仍记作un,使得 un→u 在L∞(0,T;V2+2δ) weak*; (25)式在(0,t)上积分,得到等价方程 (26) 在(26)式中n→∞,对t求导,可得u是问题(4)-(5)的解,且(u,ut)∈L∞(0,T;V2+2δ×V2δ), ut∈L2(0,T;V2+2δ),utt∈L2(0,T;V2δ-1). 所以,u∈H1(0,T;V2+2δ)⊂C(0,T;V2+2δ),ut∈H1(0,T;V2δ-1)⊂Cw(0,T;V2δ-1). 由引理1,ut∈Cw(0,T;V1+2δ).(16)式在(t0,t)上积分,得: 所以,方程在(t0,t)上是可积的.因此,(u,ut)∈C([0,T];V2+2δ×V2δ). 下证(u,ut)连续依赖X2+2δ上的初值. 设u,v是问题(4)-(5)分别对应于初值u0,u1和v0,v1的两个解,则ω=u-v满足方程 (27) ω(0)=u0-v0≡ω0, ωt(0)=u1-v1≡ω1. (27)式与Aδωt作内积,由假定(i),(ii),得: (28) (29) (30) 将(29),(30)式代入(28)式,得: 所以,解连续依赖X2+2δ上的初值,即解的唯一性得证. [1] ANDREWS G. On the existence of solutions to the equationutt-uxxt=σ(ux)x[J]. Journal of Differential Equations, 1980,35(1):200-231. [2] KOBAYASHI T, PECHER H, SHIBATA Y. On a global in time existence theorem of smooth solutions to a nonlinear wave equation with viscosity[J]. Mathematische Annalen, 1993,296(1):215-234. [3] KAVASHIMA S, SHIBATA Y. Global existence and exponential stability of small solutions to nonlinear viscoelasticity[J]. Communications in Mathematical Physics, 1992,148(1):189-208. [4] 姜礼尚,陈亚浙,等.数学物理方程讲义.第二版[M].北京:高等教育出版社,38-40. [5] ANG DD, DINH APN. Strong solutions of quasilinear wave equation with nonlinear damping[J]. SIAM Journal on Mathematical Analysis,1988,19(2):337-347. [6] NAKAO M. Existence of global smooth solution to the initial boundary value problem for the quasi-linearhyperbolic equation with a degenerate dissipative term[J]. Differ Eqs, 1992,98(1):299-327. [7] YANG Zhijian. Global attrator for the Kirchhoff type equation with a strong dissipation[J]. Differ Eqs, 2010,249(6):3258-3278. TheExistenceandUniquenessoftheGlobalSolutionstoaClassofNonlinearEvolutionEquationsofFourth-Order ZHANG Yuan-yuan1, WANG Hong-wei2 (1.Teaching and Research Department of Mathematics, Kaifeng University,Kaifeng 475000, China; 2.Department of Mathematics and Statistics, Anyang Normal University, Anyang 455000, China) The existence and uniqueness of the global solutions to a class of nonlinear evolution equations of fourth order were studied. By some standard methods the non-linear terms were estimated. By use of embedding theorem and the method of semigroup,under rather mild conditions the existence and uniqueness of the global solutions for the above-mentioned problem were obtained. global solutions; existence; uniqueness 2013-09-19 国家自然科学基金(10971199);河南省教育厅科学技术研究重点项目(13B110137);开封市科技发展计划(1401012). 张媛媛(1979-),女,河南省商丘市人,讲师,硕士,主要从事偏微分方程与无穷维动力系统的研究. 张媛媛,王宏伟.一类四阶非线性发展方程整体解的存在唯一性[J].安徽师范大学学报:自然科学版,2014,37(4):330-334. O175.29 A 1001-2443(2014)04-0330-05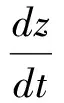
2 主要结论