岩石物理实验“四参数”关系研究
----毛细管压力、核磁共振τ2谱、电阻增大率和相对渗透率
白松涛, 万金彬, 程道解, 李戈理, 赵建斌, 杨 玲, 王明方
(中国石油集团测井有限公司 油气评价中心,西安 710077)
随着主要含油气盆地勘探开发程度的不断深入,待探明石油资源的品位明显变差,低渗透油气藏储量占中国每年总探明储量的80%以上。这类储层在微观上表现为孔隙结构复杂,在宏观上造成油气层勘探难度增大,影响试油获得率的提高。准确评价这类储层的储集性能、开采价值、采收率,进而提高油气解释精度,准确地掌握储层的孔隙结构、油藏的原始油柱高度、产能状况等信息是十分必要的。在多孔介质中,岩石核磁共振τ2谱、电阻增大率、毛管压力曲线及相对渗透率是描述储层微观结构特征的4类重要参数[1]。通常情况下,这4类参数都是在实验室中分别在一定的条件下获得,要全面描述储层微观结构特征必须花费一定的成本,而且在实验过程中受流体类型、温度、压力、仪器精确度等各种主观及客观因素的影响,所得测量结果不一定能够代表样品特征,因此针对储层微观特征研究有必要将“四类参数”进行理论方法对比、实验综合分析。
实验室中,岩心核磁共振实验具有现场快速测量、不损坏岩心及可重复性等优点,在实际生产中,核磁共振测井仪器能够获得连续纵向的地层信息,即横向弛豫时间τ2谱;毛管压力曲线、电阻增大率曲线和相对渗透率曲线都是间接通过岩石物理实验获得。但是这4类参数在润湿相流体饱和岩心实验测量过程中共同的参数纽带是饱和度,因此,从“岩心标定测井”的角度出发,研究岩石物理实验“四参数”之间的关系对于复杂储层认识和评价有很重要的指导作用。
1 国内外实验研究进展
近些年,周灿灿、运华云等人利用岩石物理实验资料对核磁共振τ2谱构造毛管压力曲线进行研究[2],在应用中形成以线性转换为主,以幂函数及特殊函数最优化方法为探索的较为成熟技术;对于核磁共振τ2谱转换电阻增大率,相关文献很少,张占松等人在对新疆某区块岩心研究的基础建立对应的双对数关系[3];核磁共振τ2谱与相对渗透率之间的关系,目前无文献描述。
Szabo(1974)描述毛管压力和电阻增大率之间近似于线性关系[4],有一定理论意义,并不能够得出毛管压力曲线和电阻增大率之间的关系。Longeron(1989)等人测量得地层条件下的毛管压力和电阻增大率[5],但是并没有指出它们之间的相关性;李克文(2006)建立了理论上的毛管压力和电阻增大率之间的关系[6],模型是基于多孔介质岩石推导所得。
Purcell(1949)提出利用毛管压力曲线计算相对渗透率[7],Burdine(1953)加入了弯曲度的影响因素[8];Brooks-Corey(1966)总结了以往的经验,改进了压汞曲线求取相对渗透率的幂函数表达式[9],被称为Brooks-Corey相对渗透率模型。
对于相对渗透率和电阻增大率之间的相关关系文献描述较少,常规方法仅仅能够测量出特定情况下的有效渗透率(通常是在束缚水饱和度)。目前大多数计算渗透率的方法都是基于孔隙度和渗透率之间的关系来计算。常规的渗透率是基于单相流体的绝对渗透率概念,而实际在井筒周围的赋存流体是以多相流体存在的。
基于以上技术调研与分析,在研究中利用冀东油田某区块26个岩样实验所得核磁共振τ2谱、电阻增大率、毛管压力曲线、相对渗透率4项岩石物理实验成果,结合各类数学物理模型,揭示核磁共振τ2谱、电阻增大率、压汞曲线、相对渗透率之间的内在关系。
2 岩石物理理论研究
随着油气田勘探开发的难度增大,以及深部油气藏、高含水油藏、低渗油气藏的开发,油层物理已成为油田勘探开发中不可缺少的理论基础。实验是油层物理研究方法的一大特点,再利用一定的数学公式进行表达,理论方法同实践结合,形成多学科渗透和创新。本次岩石物理实验涉及核磁共振τ2谱、电阻增大率、压汞曲线、相对渗透率4方面内容。核磁共振τ2谱、电阻增大率在“岩心标定测井”方面的研究及应用较为成熟,而压汞曲线、相对渗透率在油田开发及二次开发具有重要的作用。实际分析表明这4个参数描述储层有其内部共同特征,可以从理论上进行推算反演。
2.1 毛细管压力与电阻增大率的关系
地层中流体流动的空间是一些弯弯曲曲、大小不等、彼此曲折相通的复杂小孔道,这些孔道从理论上可抽象成一个多维的相互连通的毛细管网络。根据实测的水银注入压力与相应的岩样含水银体积,经计算求得水银饱和度和孔隙喉道半径后,就可绘制毛管压力、孔隙喉道半径与水银饱和度的关系曲线,即毛管压力曲线。毛管压力曲线反映了在一定驱替压力下水银可能进入的孔隙喉道的大小及这种喉道的孔隙容积,实际实验室中通过测量毛管压力曲线来研究岩石微观孔隙结构。岩石孔隙中含有油气时的电阻率比岩石孔隙中全部含水时的电阻率增大,其增大的倍数叫做电阻增大率。电阻增大率与岩石含流体饱和度有关。
Toledo等认为在一定润湿相饱和度范围内,电阻率具有分形特征,并且可以用饱和度的分形维数获取。理论认为在油气从烃源岩向储层的初次运移过程中,毛管压力是重要的动力,因而在水润湿的条件下,油、气相会在毛细管力作用下自动地由小孔隙和细喉道向较大、较粗的孔隙和喉道内运动,岩石表面附着有流体束缚水分子膜对流体流动起到阻碍作用。因此,假设2个条件:①润湿相储层的孔隙结构主要是形状规则的多孔结构,具有不同的分维数;②薄膜束缚水控制着润湿相的毛管阻力。基于此,提出在一定润湿相饱和度范围内的电阻率与含水饱和度的关系式
(1)
式中:Rt为岩石电阻率(Ω·m);Sw为含水饱和度;D为孔隙性岩石的分维数,无量纲;f为与水膜厚度及界面张力有关的拟合指数,无量纲。
同时,饱和度可用毛管压力的分形维数计算如下
Sw∝(pc)-(3-D)
(2)
式中pc为毛管压力(MPa)。
联立(1)式和(2)式可得
Rt∝(pc)1/f
(3)
当pc等于排驱压力pc,min时,Rt等于Ro(100%含水岩石的电阻率),即
Ro∝(pc,min)1/f
(4)
式中pc,min为排驱压力(MPa)。
电阻增大率作为润湿相饱和度的一种特征,Archie(1942)发表论文中的公式详细阐明了电阻增大率各变量之间的关系
(5)
式中:I为电阻率指数,无量纲;n为饱和度指数,无量纲;b为与岩石性质有关的系数,通常为1。
联立(3)式、(4)式和(5)式可得
pc=pc,minIf
(6)
对于地层流体性质一定时,即地层水电阻率、含水饱和度相同的同一岩性地层,随着岩石的孔隙结构变差,地层电阻率是逐渐增大的。在公式(6)中,毛管压力与电阻率之间存在幂函数关系,证明岩石的电学特征和孔隙结构特征具有内在联系。
2.2 毛细管压力与核磁共振τ2谱的关系
核磁共振的机理表明,氢核在孔隙中作横向弛豫运动时,会与孔隙壁产生碰撞作用。碰撞过程造成氢核的能量损失,使氢核从高能态回到低能态,即氢核的横向弛豫过程。碰撞越频繁,氢核的能量损失也越快,也就是加快了氢核的横向弛豫过程。很显然,孔隙的大小决定了氢核与孔隙壁碰撞过程的多少,孔隙越小,则氢核在做横向弛豫的过程中,与孔隙壁的碰撞机率越大。由此得出孔隙的大小与氢核的弛豫率成反比关系(即孔隙越小,氢核的横向弛豫率越高),这就是应用核磁共振τ2谱研究岩石孔隙结构的理论基础。
国内外许多学者认识到孔隙表面是一种分形结构。由于分形结构与幂函数有密切关系,毛管压力曲线反映的是某一孔喉大小控制下的孔隙体积分布,τ2谱则反映不同孔隙大小的孔隙体积分布,核磁共振横向弛豫时间τ2谱与实验室测量毛管压力曲线均在一定程度上反映了岩石的孔隙结构特征,二者之间具有很好的相关性,因此,利用幂函数关系对τ2谱累计曲线转换毛管压力曲线,即:
(7)
式中m、n值为转换参数,无量纲;τ2为核磁共振横向弛豫时间(ms)。
由(7)式可知,pc与τ2之间是一一对应的关系,pc,min对应于τ2,max,即
(8)
式中,τ2,max为核磁共振最大响应横向弛豫时间(ms)。
由以上分析知,核磁共振τ2谱分布与实验室毛管压力曲线之间具有相关性,二者均在一定程度上反映了岩石的孔隙结构。
2.3 核磁共振τ2谱与电阻增大率的关系
实际分析表明,核磁共振τ2谱与压汞、压汞与电阻增大率之间存在一定的相关关系,那么核磁和电阻增大率之间必然也存在一定的内在相关性。将(7)式、(8)式带入(6)式中,同时令Α= -n/f,Β= (τ2,max)n/f,可得核磁共振τ2谱与电阻增大率I的理论关系式
(9)
从式(9)可以看出,I与核磁共振τ2谱在双对数坐标下应具有线性关系,这种关系可以通过实验获取的核磁共振τ2谱与I之间的线性相关性回归关系加以证明。2个参数在双对数坐标下具有较好的线性相关关系,并通过拟合可以获取系数A和B。
2.4 电阻增大率与相对渗透率的关系
在多相流体流动过程中,各相间会发生相互作用、干扰和影响,实验室采用相对渗透率来表征岩石和流体间相互作用的动态特征。所谓相对渗透率是指多相流体共存和流动时,岩石让其中某一相流体通过能力的大小。在实际应用中,为了应用方便(将渗透率无量纲化),也为了便于对比各相流动阻力的比例大小,引入相对渗透率的概念。
李克文(2007)推导出相对渗透率和电阻增大率之间的关系。
(10)
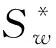
(11)
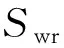
可知,岩石润湿相的相对渗透率可以由公式(10)计算得出,而残余油饱和度是可以通过多孔介质的电阻增大率测量得到。
对于岩石润湿相的相对渗透率可以通过公式(10)得出,而描述非润湿相条件下的相对渗透率不能用公式(10)计算,而是结合计算所得的润湿相相对渗透率,首先计算出孔径分布指数,再利用孔径分布指数和岩石非润湿相之间的相对关系进行计算,具体如下。
Purcell(1949)利用数值模拟和数理统计方法,通过岩石的孔径分布推导出岩石润湿相相对渗透率公式
(12)
其中λ是孔径分布指数,无量纲。
λ也可以直接从毛管压力曲线中计算出来。利用公式(10)计算出来润湿相的相对渗透率后,再利用公式(12)推断出孔径分布指数λ值。
根据Brooks-Corey模型(1966)和Li-Horne(2006)的研究,岩石非润湿相相对渗透率可以通过表达式(13)进行计算如下
(13)
式中krnw为油相相对渗透率。
根据分析可得,润湿相和非润湿相条件下的相对渗透率可以利用电阻率增大率进行计算,即利用公式(10)和(13)。岩石的相对渗透率反映的是不同饱和度条件下油相和水相的相对渗透率大小,当岩石孔隙含多相流体时,以亲水砂岩为例,油处于孔隙的中央部位,四周被水包围。由于油的电阻率高,所以岩性相同的含油岩石与含水岩石相比,电流经过的路径变得更加曲折,在其他条件相同的情况下,含油岩石的电阻增大率、电阻率比含水岩石的地层大得多,说明储层岩石的电学性质能够在一定程度上表征岩石孔隙中润湿相和非润湿相相对渗透性以及润湿性质。
2.5 毛细管压力与相对渗透率的关系
毛细管压力曲线反映岩石的孔喉分布,因此根据毛管压力曲线所确定的孔喉分布以及不同孔喉对流体渗流能力不同可计算出岩石渗透率;另一方面,相对渗透率主要取决于流体饱和度,而毛管压力的大小也直接与润湿相、非润湿相饱和度有关系:因此,通过恰当的毛管压力函数转化,根据岩石内流体饱和度的变化特征来计算相对渗透率也是可能的。
实验分析表明,当外加压差可以克服某一毛管力(pc)i时,在孔道半径大于ri=2σcosθ/(pc)i的孔道中将只有油存在和流动;而孔道半径小于ri的那些孔道中只有水存在和流动。设在上述两种情况下岩石中的含水饱和度为Si,那么小于ri的孔道中,含水饱和度必然小于Si,可以认为岩石中含水饱和度为Si时,水和油的有效渗透率分别为
(14)
(15)
kw为水相渗透率(10-3μm2);ko为油相渗透率(10-3μm2);θ为润湿角(°);λ为校正系数,无量纲;φ为孔隙度;Si为含水饱和度;pc为毛细管压力(MPa)。
而水和油的相对渗透率则为
(16)
(17)
在不同的含水饱和度Si下,利用公式(16)和公式(17)便可求出相应的krw和kro,从而可得出油水相对渗透率和含水饱和度的关系曲线。公式(16)和(17)是基于毛细管束模型推导出来,与实际孔隙结构有一定的差距,计算结果可能会有一定的差别。
2.6 核磁共振τ2谱与相对渗透率的关系
理论分析及实验表明,核磁共振τ2谱反映岩石的孔隙结构,与毛管压力曲线之间为幂函数关系[公式(7)],而岩石相对渗透率和毛管压力之间的关系推算如公式(16)和(17),因此核磁共振τ2谱和相对渗透率之间有一定的关系。
将公式(7)带入公式(16)和(17)中可得
(18)
(19)
分析可知,核磁共振τ2谱和相对渗透率呈对数关系,通过实验获取的核磁共振τ2谱与krw和kro之间的线性回归或图解法得到验证,并最优化求解可以获取相关系数。
3 实验设计及测试
实际理论推算证明,岩石物理实验“四参数”存在内在关联,这种关联性是由饱和度及孔隙结构引起的。实际研究中利用分形理论等各种理论方法,也证明了4种岩石物理实验能够分别独立求取岩心的束缚水饱和度大小、渗透率大小及孔径分布情况,这对于认识储层是非常重要的,因此总结“四参数”内部变量关系如图1。
为证明以上理论分析正确,现选取冀东油田南堡凹陷XX井区沙一段26块岩心,按照实验过程对岩心的破坏程度,以及实验的由易到难的难度级别,将每颗岩样分成两部分,先利用第一部分进行核磁测量和电阻增大率测量。通过实验室测试,首先将一部分测量,得到孔隙度、渗透率等常规参数;然后完全饱和6 g/L氯化钠溶液,测量得到完全饱和水时的核磁τ2衰减谱;再利用仪器20.54 MPa离心后,测量得到束缚水条件下的核磁τ2衰减谱。重新饱和相同矿化度的氯化钠液体,使用煤油等进行驱替,测量得到岩石的岩电参数,从而获得电阻增大率和含水饱和度之间的关系;然后在相同实验室条件下,对每块岩石的另外一部分进行不同程度的饱和驱替,测量得到相对渗透率;最后,再对岩样进行毛管压力驱替测量。实际实验流程图如图2。
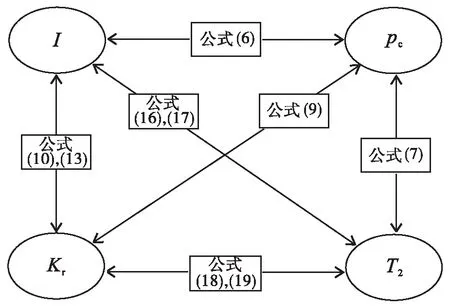
图1 岩石物理“四参数”之间关系Fig.1 Relationship between the four petrophysical parameters
表1为26块岩样中的8块具有代表性的岩样测试结果。岩石学分析表明该地区以岩屑长石细砂岩为主,孔隙空间主要为粒间孔和少量溶蚀孔,岩心孔隙度为9.48%~18.9%,渗透率为(1.723~213)×10-3μm2,属于碳酸氢钠水型,矿化度在5~7 g/L之间。本次实验中,相对渗透率测试所用基本参数——模拟油黏度为4.5 mPa·s,模拟油为中性煤油,测定温度50℃;电阻增大率测试所用基本参数——测定温度25℃,地层水φ为孔隙度(%);K为渗透率(10-3μm2);ρ为岩石密度(g/cm3);Ka为水相渗透率(10-3μm2);Ko为油相渗透率(10-3μm2);Swi为束缚水饱和度(%);Sor为残余油饱和度(%);b为电阻增大率系数;n为饱和度系数;τ2,cutoff为τ2截止值(ms);τ2,g为几何均值(ms);pc为排驱压力(MPa);SHg,max为最大汞饱和度(%)。

图2 岩心实验流程Fig.2 The processing of core experiments
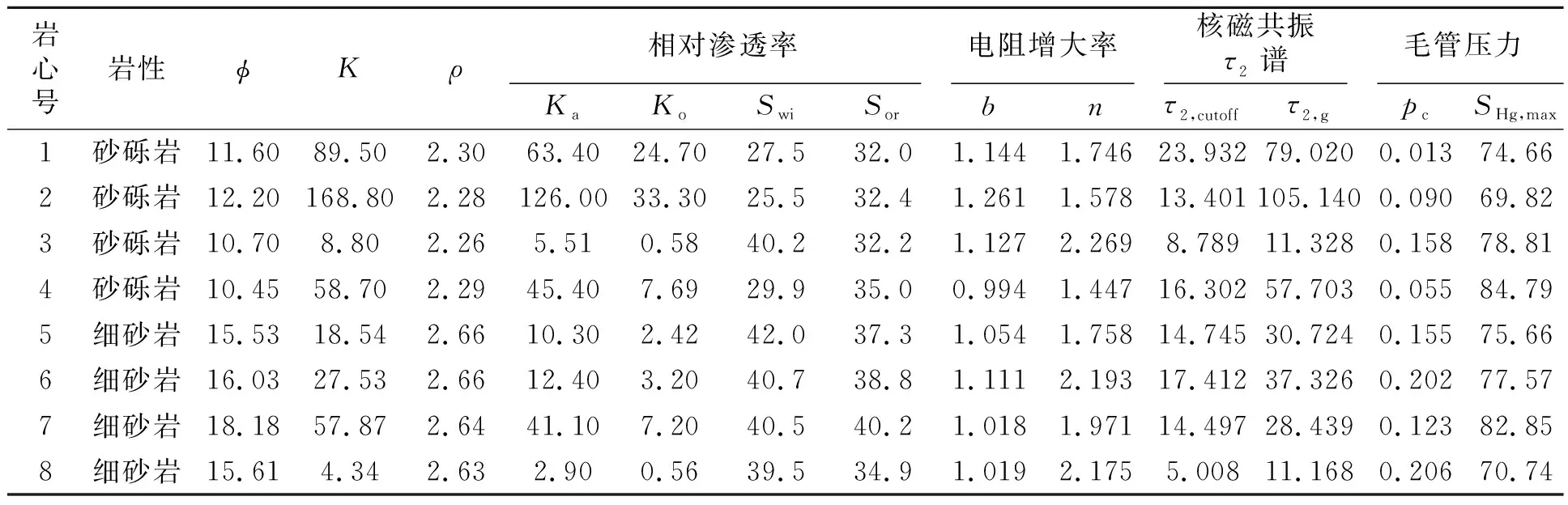
表1 岩心实验测量分析结果Table 1 The result of core experiments
电阻率Rw为0.95 Ω·m;核磁共振测试所用基本参数——回波间隔为0.6 ms,等待时间为6 s,回波个数为4096,扫描次数128,测试温度25℃;毛管压力测试所用测量基本信息——温度为20℃,湿度为55%。实验样品测量结果信息如表1。
4 实验效果分析
4.1 四参数之间相关性分析
为了验证四参数之间的相关性,针对8块岩样在一定的润湿相饱和度范围内四参数之间两两的关系拟合,如图3~图8所示。
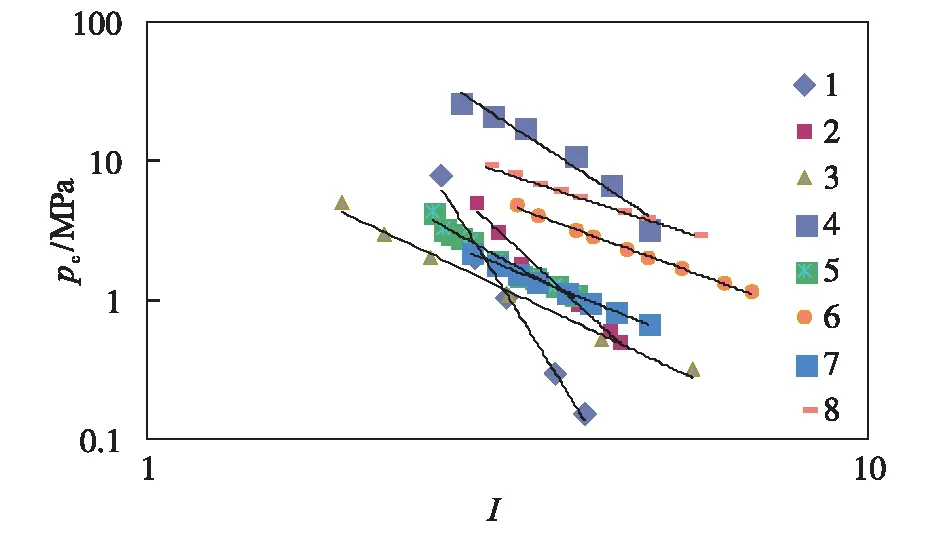
图3 毛管压力与电阻率增大率的关系Fig.3 Relationship between capillary pressure and resistivity index
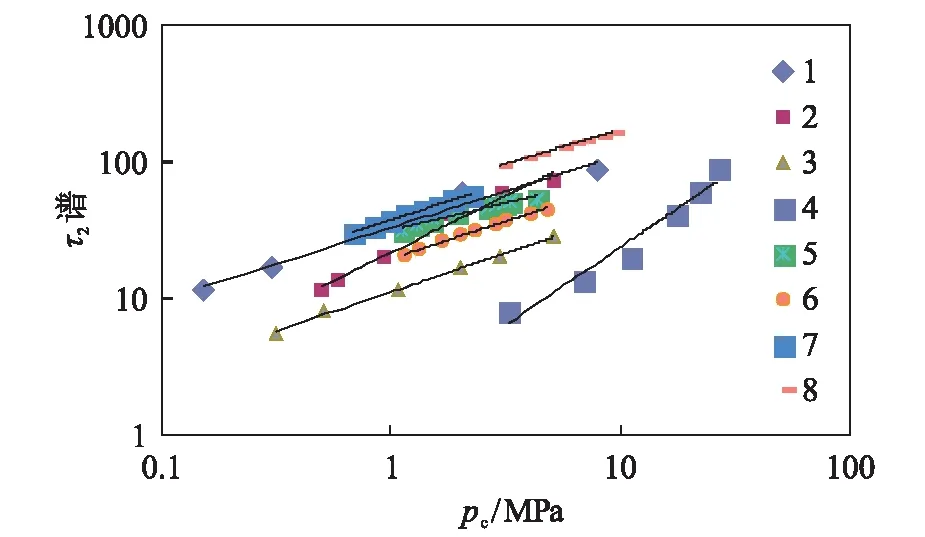
图4 毛管压力与核磁共振τ2谱的关系Fig.4 Relationship between capillary pressure and NMR τ2 distribution
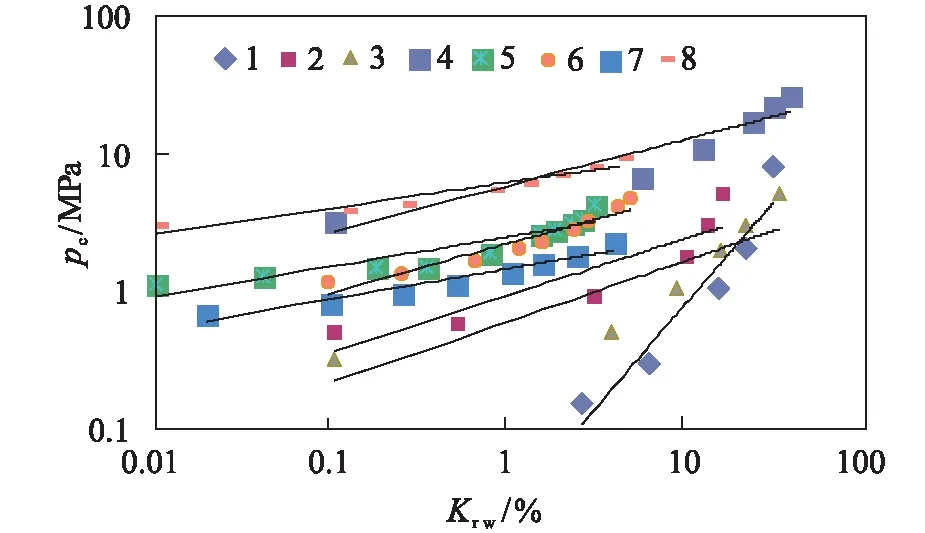
图5 毛管压力与润湿相相对渗透率的关系Fig.5 Relationship between capillary pressure and relative permeability
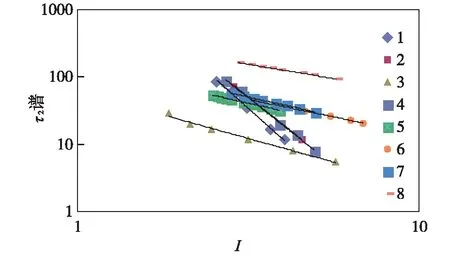
图6 电阻增大率与核磁共振τ2谱的关系Fig.6 Relationship between resistivity index and NMR τ2 distribution
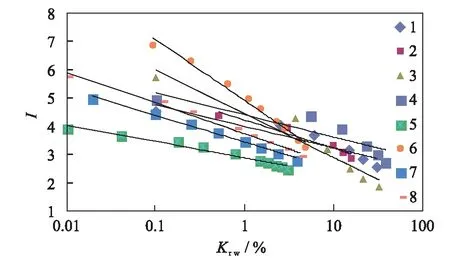
图7 电阻增大率与润湿相相对渗透率的关系Fig.7 Relationship between resistivity index and relative permeability
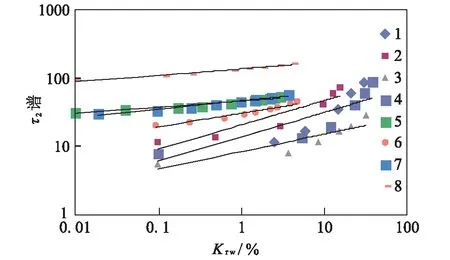
图8 核磁共振τ2谱与润湿相相对渗透率的关系Fig.8 Relationship between NMR τ2 distribution and relative permeability
通过对图3中8块岩样的毛管压力和电阻率增大率进行幂函数拟合,可以得出岩样实验参数之间的相关系数均达到0.86以上;通过对图4中8块岩样的毛管压力和核磁共振τ2谱进行幂函数拟合,可以得出岩样实验参数之间的相关系数均达到0.97以上;通过对图5中8块岩样的毛管压力和润湿相相对渗透率进行对数拟合,可以得出岩样实验参数之间的相关系数均达到0.93以上;通过对图6中8块岩样的电阻增大率和核磁共振τ2谱进行双对数拟合,可以得出岩样实验参数之间的相关系数均达到0.88以上;通过对图7中8块岩样的电阻增大率和润湿相相对渗透率进行对数拟合,可以得出岩样实验参数之间的相关系数均达到0.92以上;通过对图8中8块岩样的核磁共振τ2谱和润湿相相对渗透率进行指数拟合,可以得出岩样实验参数之间的相关系数均达到0.91以上。
基于分析验证,将26块岩心的对比、转换关系总体符合情况进行整理,如表2。
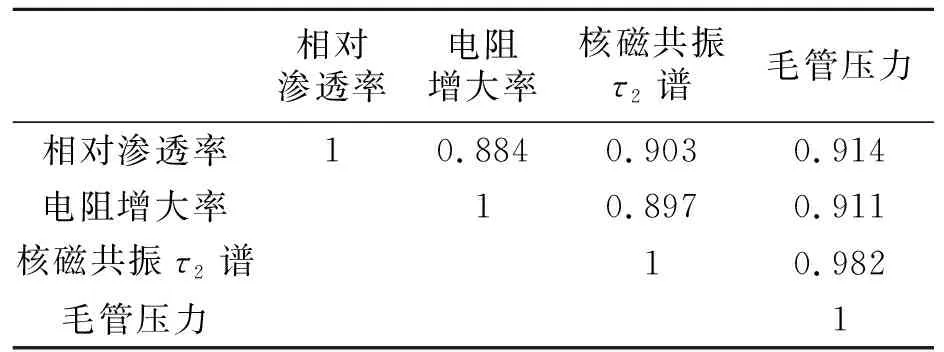
表2 岩心实验测量值相互转换拟合度结果Table 2 The fit result of the interchanging core test data
4.2 不同数据源转换对比分析
为了检验各类岩石物理参数之间转换的优劣差别,将实验所得不同数据源转换为同一类参数进行差异性分析。针对同一颗岩样分别对毛管压力、核磁共振τ2谱、电阻增大率、相对渗透率四类参数,采用不同的数据源转换为同一参数进行结果对比,如图9~图12所示。
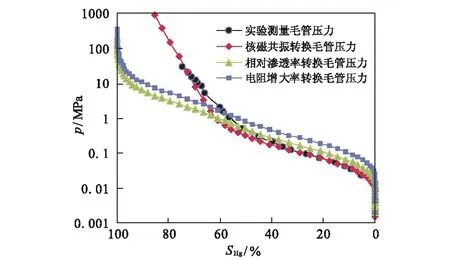
图9 不同数据源转换毛管压力曲线Fig.9 Different data is converted into capillary pressure
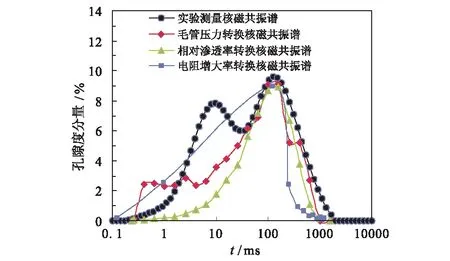
图10 不同数据源转换核磁共振τ2谱Fig.10 Different data is converted into NMR τ2 distribution
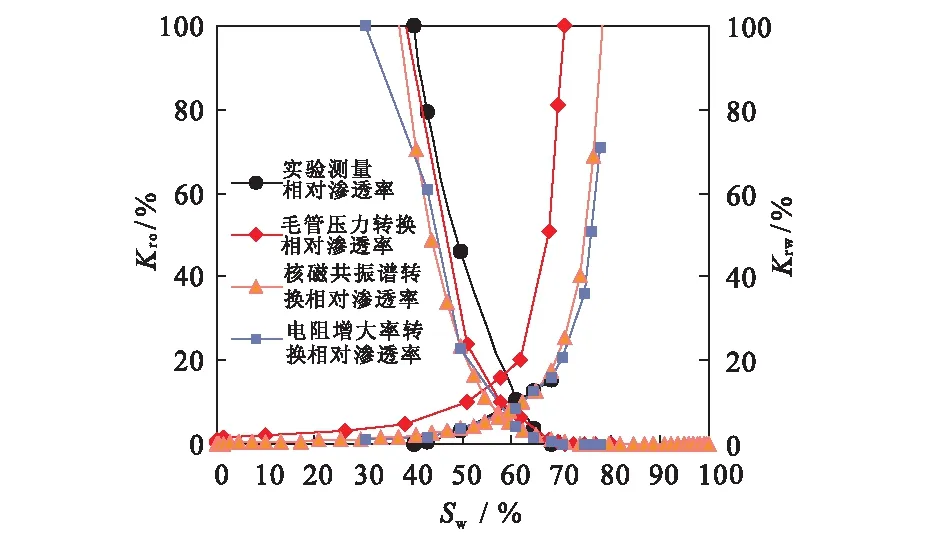
图11 不同数据源转换相对渗透率Fig.11 Different data is converted into relative permeability
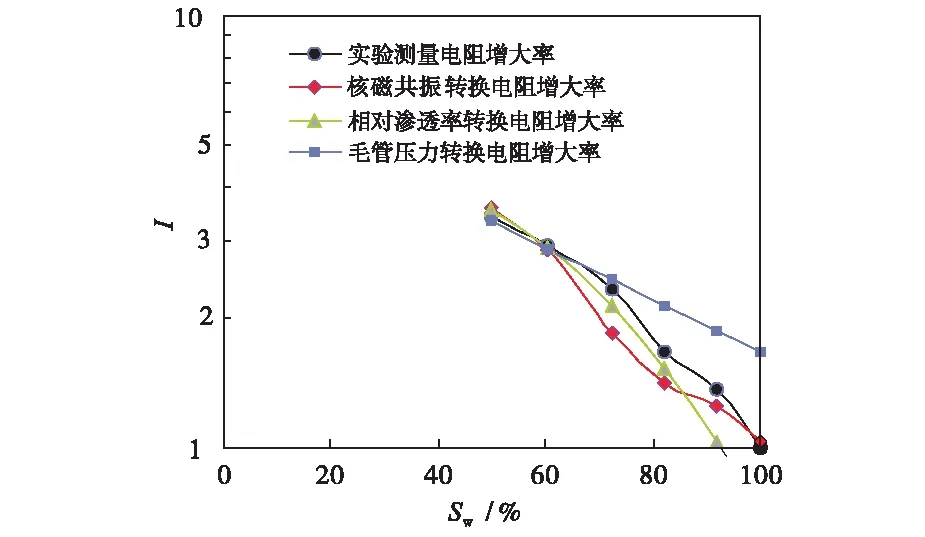
图12 不同数据源转换电阻增大率Fig.12 Different data is converted into resistivity index
在实际勘探开发中,毛细管压力用于定量分析岩石的孔隙结构性质,核磁用于描述孔隙内流体赋存状态,电阻增大率用来表征岩石的含油气性,相对渗透率用以判别润湿性以及多相流体的相对流动能力。不同的岩样由于其物性和孔隙结构以及润湿性的不同,因此,针对不同岩样进行同一类转换中存在着转换系数的不同,相同岩样采用不同的数据源进行转换时存在一定的误差。以毛管压力曲线和核磁共振τ2谱转换为例,薄膜束缚水部分的存在引起τ2分布反映的孔隙空间与毛管压力曲线反映的孔隙空间有差异。另外,毛管压力反映孔喉之间的连通关系,反映的是最小喉道和其所连通孔隙的半径和体积,且只能反映进汞部分对应的孔喉空间;NMR岩心实验τ2谱分布反映的是所有孔隙喉道半径大小,致使在相互转换时存在一定的差异性。
通过对四参数之间两两相关性研究,结合不同数据源转换为同一岩石物理实验数据,对比分析得出:针对孔隙结构的评价精确度由高到低分别为毛管压力、核磁共振、岩电参数、相对渗透率,其中后3类参数转换为毛管压力精度逐渐降低;针对孔隙流体赋存状态的评价精确度由高到低分别为核磁共振、毛管压力、相对渗透率、岩电参数,其中后3类参数转换为核磁共振精度逐渐降低;针对岩石的含油气性的评价精确度由高到低分别为岩电参数、核磁共振、相对渗透率、毛管压力,其中后3类参数转换为岩电参数精度逐渐降低;针对多相流体相对流动能力的评价精确度由高到低分别为相对渗透率、岩电参数、核磁共振、毛管压力,其中后3类参数转换为岩电参数精度逐渐降低。研究中所用实例为中-高孔渗砂岩储层,对于低孔渗、超低渗及双重孔隙储层的情况有待进一步研究和验证。
基于以上理论分析和实验对比研究,利用Excel的数据存放功能,进行Vba编程,将岩石物理四参数转换关系形成模块方便实际生产和研究使用,界面如图13。
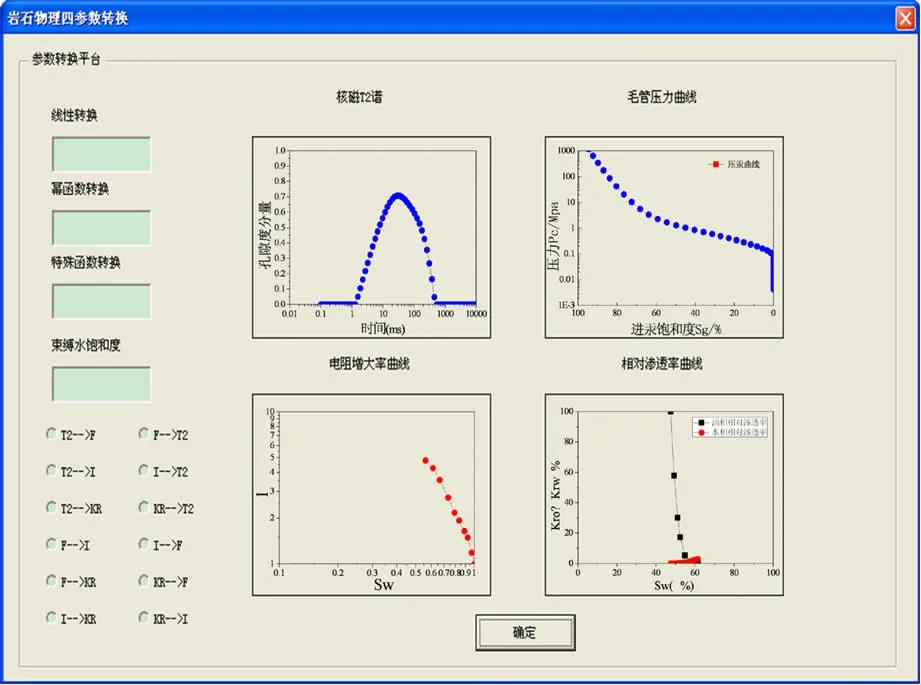
图13 岩石物理“四参数”转换关系界面Fig.13 Interface of converting of the four petrophysical parameters
5 结论与认识
a.基于“四参数”的相互转换关系,创新推导出核磁共振τ2谱与相对渗透率之间关系的理论模型,认为核磁共振τ2谱与相对渗透率在一定润湿相饱和度范围内具有对数关系,并在实际岩石物理实验中得到验证。
b.通过数学公式推导分析,可以得出岩石物理实验“四参数”之间有相关性:其中毛细管压力与核磁共振τ2谱之间呈幂函数关系,毛管压力曲线与相对渗透率呈对数关系,毛管压力曲线与电阻增大率之间呈幂函数关系,核磁τ2谱与电阻增大率之间呈幂函数关系,核磁τ2谱与相对渗透率之间呈对数关系,电阻增大率和相对渗透率呈指数关系。
c.实验室条件下,受仪器测量精度以及一些主观因素的影响,实验数据会存在一定的误差,通过“四参数”之间的相互转换,既能够提高数据测量的精度,又能够通过组合实验获得岩心的一些隐含参数。
d.在实际勘探开发中,毛细管压力用于定量分析岩石的孔隙结构性质,核磁用于描述孔隙内流体赋存状态,电阻增大率用来表征岩石的含油气性,相对渗透率用以判别润湿性以及多相流体的相对流动能力,“四参数”紧密结合,能够较好地基于岩石物理实验对储层的产能情况进行全面分析。
[参考文献]
[1] 何更生,唐海.油层物理[M].北京:石油工业出版社,2011.
He G S, Tang H. The reservoir Physics [M]. Beijing: Petroleum Industry Press, 2011. (In Chinese)
[2] 运华云,赵文杰,周灿灿,等.利用τ2分布进行岩石孔隙结构研究[J].测井技术,2002,26(1):18-21.
Yun H Y, Zhao W J, Zhou C C,etal. Re-searching rock pore structure with T2distribution[J]. Well Logging Technology, 2002, 26(1): 18-21. (In Chinese)
[3] 张冲,张占松,宋秋强.核磁共振横向弛豫时间τ2谱与电阻率增大系数的关系[J].吉林大学学报:地球科学版,2012, 42(2):424-428.
Zhang C, Zhang Z S, Song Q Q. Relationship between NMR T2distribution and resistivity index[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(Sup.2): 424-428. (In Chinese)
[4] Szabo M. New methods for measuring imbibition capillary pressure and electrical resistivity curves by centrifuge[J]. Old SPE Journal, 1974, 14(3): 243-252.
[5] Longeron D G, Argaud M J, Bouvier L. Resistivity index and capillary pressure measurements under reservoir conditions using crude oil[C]//SPE Annual Technical Conference and Exhibition. San Antonio: SPE19589, 1989: 187-200.
[6] Li K W. A new method for calculating two-phase relative permeability from resistivity data in porous media[J]. Transport in Porous Media, 2008, 74(1): 21-33.
[7] Purcell W R. Capillary pressures-their measurement using mercury and the calculation of permeability therefrom [J]. Journal of Petroleum Technology, 1949, 1(2): 39-48.
[8] Burdine N T. Relative permeability calculations from pore size distribution data [J]. Journal of Petroleum Technology, 1953, 5(3): 71-78.
[9] Brooks R H. Properties of porous media affecting fluid flow[J]. Journal of the Irrigation and Drainage Division, 1966, 92: 61-88.

