线性模型中数据扰动对模型参数的影响

程鹏鹏，曹连英

(东北林业大学，哈尔滨150040)

线性模型是一类统计模型的总称，它包括线性回归模型、方差分析模型、协方差分析模型和线性混合效应模型等.线性模型在许多生物、医学、经济、管理、地质、气象、农业、工业、工程技术等领域都普遍使用.因此线性模型成为现代统计学中应用最为广泛的模型之一[1].

经典最小二乘方法假设自变量的观测是精确的，仅仅因变量存在测量误差.事实上，这种假设是不现实的，自变量在取样、人为、仪器误差的影响下同样存在误差扰动.因此需要含误差变量的线性模型，我们把自变量带有误差的模型简称EIV模型.近几年EIV模型以及关于模型的深入探索Fekri and Ruiz － Gazen[2]和 He Xuming and Liang Hua[3]等都对这一模型进行了进一步的研究.

本文基于矩阵扰动分析理论，给出线性模型在扰动下仍然可估的充分条件，并进一步讨论了线性模型数据扰动对模型参数的影响，给出参数的扰动估计式.

1 预备知识

设线性模型

其中y为n×1观测向量，X为n×p的设计矩阵，β为p×1未知参数向量，e为随机误差，σ2为误差方差 σ2＞0.

若 rank(Xn×p)=p，则 X'X 可逆，这时=X'X－1X'y，且有)，即是β的无偏估计，这时我们称=X'X－1X'y为β的最小二乘估计.

若 rank(Xn×p)＜ p，则不是β的无偏估计，表明β没有线性无偏估计，此时我们称 β 是不可估的[4].

引理1[5]A是Hermite阵并且是满秩矩阵，其特征值为λ1≥λ2≥…≥λn;A+E为Hermite阵其特征值为1≥2≥ … ≥n，如果 η = ‖A－1/2EA－1/2‖2≤1，其中 A1/2为 A 的 Hermite平方根，那么有

2 线性模型参数的可估性

实验中得到的数据与实际数据之间会有误差，这就会出现数据的扰动问题，进而会影响线性模型的参数估计结果，定理1给出了设计矩阵扰动范围的大小，从而解决了扰动后设计矩阵的亏秩问题.

定理1:设X为n×p的实的设计矩阵，且rank(Xn×p)=p;记 A=X'X，A 的特征值为 λ1≥λ2≥…≥λp，设计矩阵 X的扰动为 ΔX，A+ΔA=(X+ΔX)'(X+ΔX)，则当设计矩阵ΔX满足:时，其中0＜ρ＜1为常数，则扰动后模型y=(X+ΔX)β+e仍可估.

证明:A=X'X为实对称阵，是Hermite阵，其特征值为 λ1≥λ2≥…≥λp＞0，A+ΔA(X+ΔX)'(X+ΔX)也是 Hermite阵，记其特征值为也是 Hermite 矩阵.

令

η = ‖A－1/2ΔAA－1/2‖2

又 ΔA=ΔX'X+X'ΔX+ΔX'ΔX 是 Hermite阵，于是

2‖(ΔX‖2‖X‖2+‖(ΔX‖22≤ρλmin(A)

则

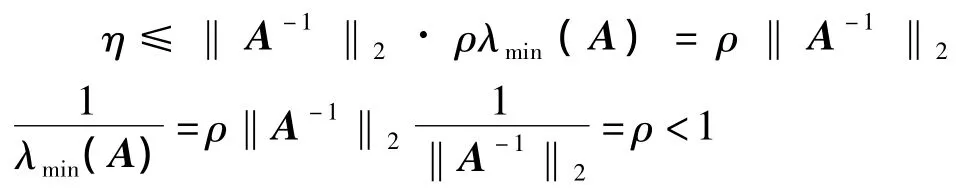
这里

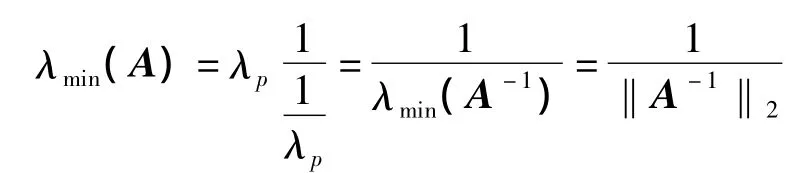
由引理1，可得

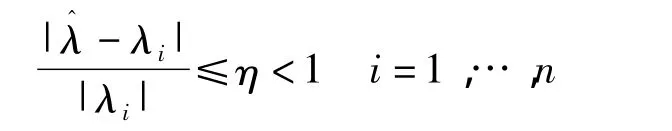
在定理1的条件下，扰动后线性模型参数仍是可估的.接下来给出在此条件下，扰动对线性模型参数的影响.

3 数据扰动对线性模型参数的影响

定理1解决了设计矩阵出现扰动可能出现的亏秩问题，下面讨论在矩阵扰动前后秩不变的情况下，扰动ΔX、Δy对的影响.

引理 2[6]设 A∈Cn×n是非奇异阵，b∈Cn，x 是方程AX=b的解，又设B=A+ΔA，满足条件‖A－1‖2‖ΔX‖2＜1，则方程(A+ΔA)(x+Δx)=b+Δb有惟一解x+Δx，并且满足不等式，其中 k=‖A‖2‖A－1‖2，r=1 －k‖ΔA‖2./‖A‖2＞0.

定理2:设X为n×p实的设计矩阵，且rank(Xn×p)=p，是线性模型(1)的最小二乘无偏估计;ΔX，Δy分别为设计矩阵X和y的扰动矩阵，=X+ΔX～=y+Δy，线性模型(1)扰动后的线性模型为=，其最小二乘估计为 若记 A=X'X，则当

时，其中0＜ρ＜1，则有

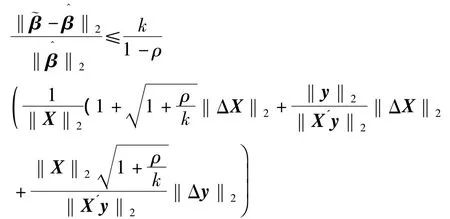
其中k=‖A‖2‖‖A－12.

证明:线性模型(1)的最小二乘解为正规方程X'Xβ=X'y的解，而线性模型=的最小二乘解为正规方程=的解.记 A=X'X，A+ΔA=(X+ ΔX)'(X+ ΔX)，ΔA= ΔX'X+X'ΔX+ΔX'ΔX，则线性模型=的正规方程为

(A+ΔA)β=X'y+Δb

其中 Δb= ΔX'·y+X'Δy+ΔX'Δy.注意到

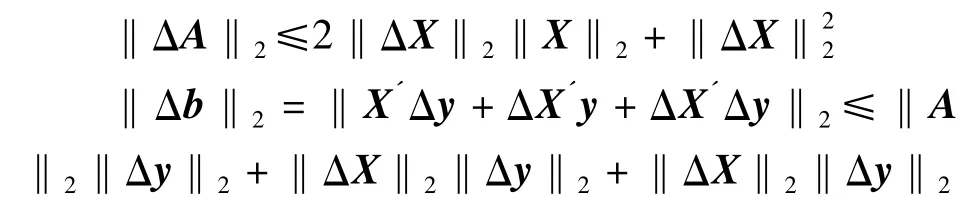
因此

其中 k= ‖A‖2‖A－1‖2.于是

又

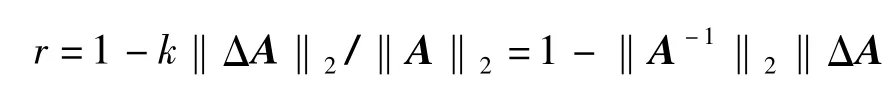
其中

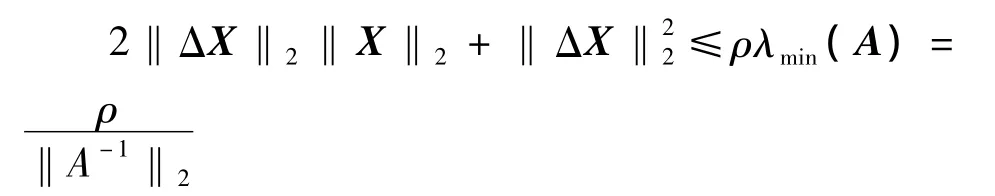
所以

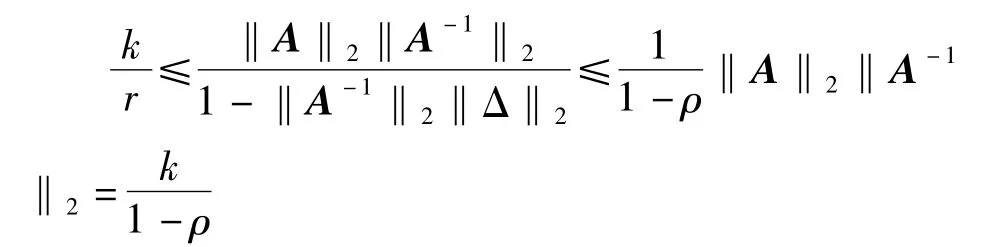
因此线性回归模型的相对扰动的一个上界为

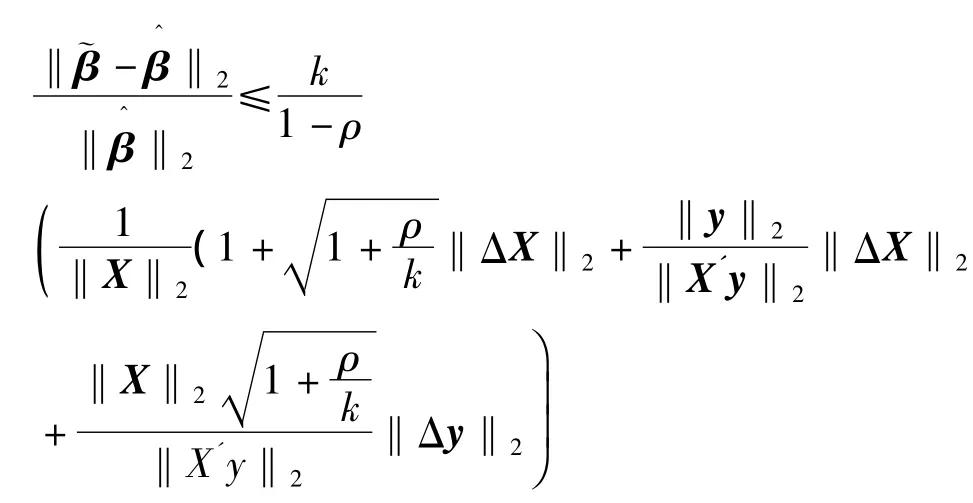
结论得证.

4 结语

对带有扰动的设计矩阵线性模型进行探讨，是扰动问题研究的一种扩展.实验中由于取样、人为、仪器误差所产生的数据有时扰动很大，为了扰动后线性模型的可估性设定了扰动数据的范围.本文在特征值扰动的基础上，从线性模型设计矩阵扰动的角度探讨了扰动后的模型可估的充分条件，给出了可估的扰动数据范围并在此基础上进一步分析了扰动数据对模型参数的影响.本文结果为优化线性模型的实验设计提供理论依据.

[1]王松桂.线性统计模型:线性回归与方差分析[M].北京:高等教育出版社，1999.

[2]FEKRI M，RUIZ－GAZEN A.Robust estimation in the simple errors－ in － variables model[J].Statistics＆Probability Letters，2006，76:1741－1747.

[3]HE X，LIANG H.Quantile regression estimates for a class of linear and partially linear errors－in－variables models[J].Statist.Sinica，2000，10:129 －140.

[4]王松桂.线性模型引论[M].北京:科学出版社，2004.

[5]DOPICO F M，MORO J，MOLERA J M.Weyl－ type relative perturbation bounds for eigensystems of Hermitian matrices[J].Linear Algebra and Its Applications，2000，309:3 －18.

[6]孙继广.矩阵扰动分析[M].北京:科学出版社，1987.