基于Collocation积分的GPS轨道仿真

栗 靖，朱伟刚，张 婷，杨 华

(北京卫星导航中心，北京 100094)

0 引 言

对GPS卫星来说，某时刻卫星在惯性坐标系中的位置、速度、加速度矢量和地球的非球形引力、日月引力、地球固体潮摄动、太阳辐射压力和Y轴偏差加速度等作用在卫星上各摄动加速度的影响，主要与太阳光压有关,在轨道仿真中，这些参数是至关重要的[1]。GPS导航系统精密定轨中，太阳光压摄动模型较多，本文采用基于Collocation积分的EROCK模型进行轨道仿真，这种模型利用附加确定性参数的方法可以提高模型精度，并且通常可满足1 m精度的定轨要求。

1 ECOM模型

ROCK模型是GPS数据处理软件BERNE所采用的太阳光压摄动模型。它根据卫星结构及材料的反射和吸收特性，将卫星表面分成若干块，并考虑各个部分之间的遮挡，计算出每一块在星固系x轴和z轴方向的摄动分量，求和得出太阳光压摄动力。为了得到更高精度的太阳光压模型，Beutler等人在ROCK模型的基础上，提出ECOM模型。由于在长弧段数据中，ROCK光压模型误差还存在与轨道周期一样的共振部分，通过对星固坐标系三个坐标轴加速度各方向增加三角函数项[2]。

在ECOM模型中，卫星加速度为

aRPP=aROCK+D(u)eD+Y(u)eY+X(u)eX，

(1)

式中：aROCK为ROCK4/42模型的加速度；eD,eY,eX为星固坐标系的坐标轴的三个单位矢量；

D(u)=D0+DCucosu+DSusinu

Y(u)=Y0+YCucosu+YSusinu，

(2),

X(u)=X0+XCucosu+XSusinu

其中，u为自变量，近似等于卫星近地点角距与平近角之和。

在GPS仿真过程中，输入参数除了6个开普勒根数外，还需输入ECOM模型中的9个光压模型参数即：D0、DCu、DSu、Y0、YCu、YSu、X0、XCu、XSu.

2 轨道仿真

2.1 初值计算

在仿真过程中可能提供三种初始条件：

2) 仿真起始时刻t0的开普勒轨道根数σi(t0)(i=1,…,6)；

3) 两个时刻t1、t2的卫星位置矢量r(t1)、r(t2)(其中仿真起始时刻t0满足关系t1≤t0≤t2)；

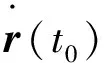
2.2 轨道外推

轨道外推的主要思想是用数值方法解具有初值问题的微分方程[3]， 具体步骤如下：

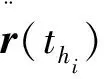
5) 由时间区间[t0,t1]两端的位置矢量和各个节点的加速度矢量拟合成多项式

y=a0+a1x+a2x2+…+aQ+1xQ+1.

(3)

6) 用上一步求取的多项式系数计算各节点的位置矢量r；

7) 将卫星运动方程泰勒展开至一阶：

(4)

8) 重复进行第5、6、7步，直至中间节点两次计算结果的差值小于0.1；

9) 存储这一步长的多项式系数；

3 仿真结果分析

轨道仿真的关键是仿真起止时间、步长和步长内多项式的系数，比用精密星历格式存储所占空间小，并且能方便的计算任意历元的卫星位置、速度、加速度和加加速度矢量，分别验证外推轨道的精度以及用多项式系数计算加速度和加加速度方法的正确性。为评价基于Collocation积分方法的轨道仿真精度，把仿真的轨道以15 min间隔写成精密星历格式，并与IGS精密星历进行比较，求出其与IGS星历的各坐标轴的差值[4-5]。

目前IGS分析中心提供的后处理精密星历，是根据全球分布的IGS测轨站所收集的数据进行计算的星历，其后处理星历定轨精度平均为5 cm，跟踪网核心站的地心坐标精度为几个厘米。其初始值是用IGS精密星历求取，除去仿真期间轨道有机动的卫星,经统计分析，得出外推5天各轴精度均在16 m以内。表1示出了2012年不同时间(共6次)各卫星外推精度的统计结果)[6]；图1示出了2012年5、6月份PRN3卫星的外推精度。从所列图表中可以看出，相同卫星在不同时期外推精度不同，有的发散较快，有的发散较慢，这主要是因为初始值的精度不同所造成的。从图2可以看出本文对PRN3卫星(外推期间0307-0312)的初始值人为的加了误差，轨道发散较加误差前明显快[7]。

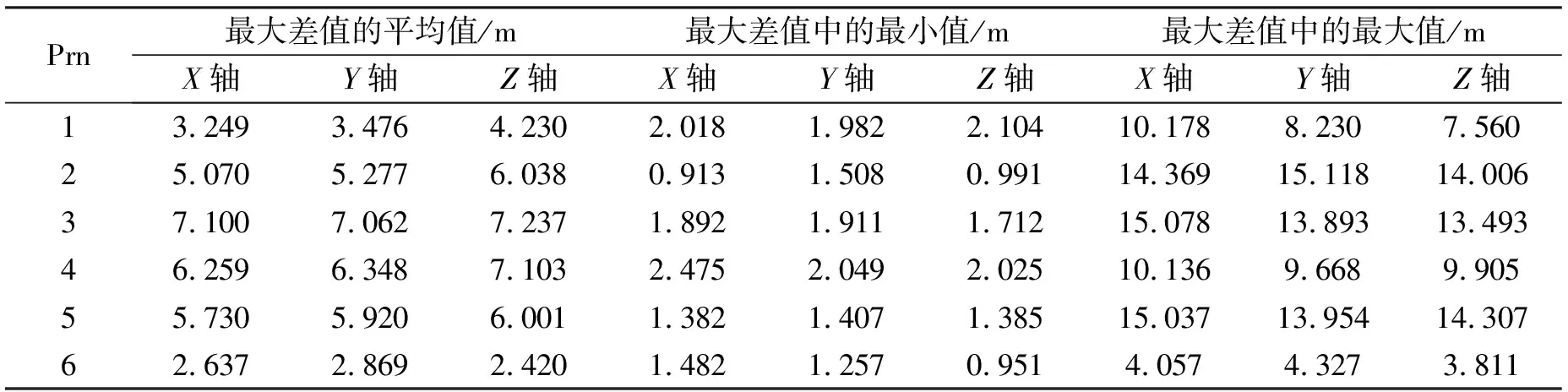
表1 2012年不同时间(共6次)各卫星外推精度的统计结果

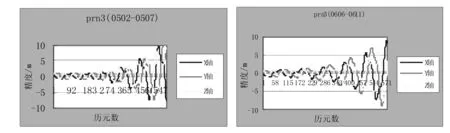
图1 PRN3卫星2012年5、6月份轨道外推精度

利用步长内的多项式系数可以很方便的求取任意历元的卫星加速度、加加速度矢量，这比用卫星运动方程计算不仅数值上能保证精度，而且快捷。具体数据如表2所示。

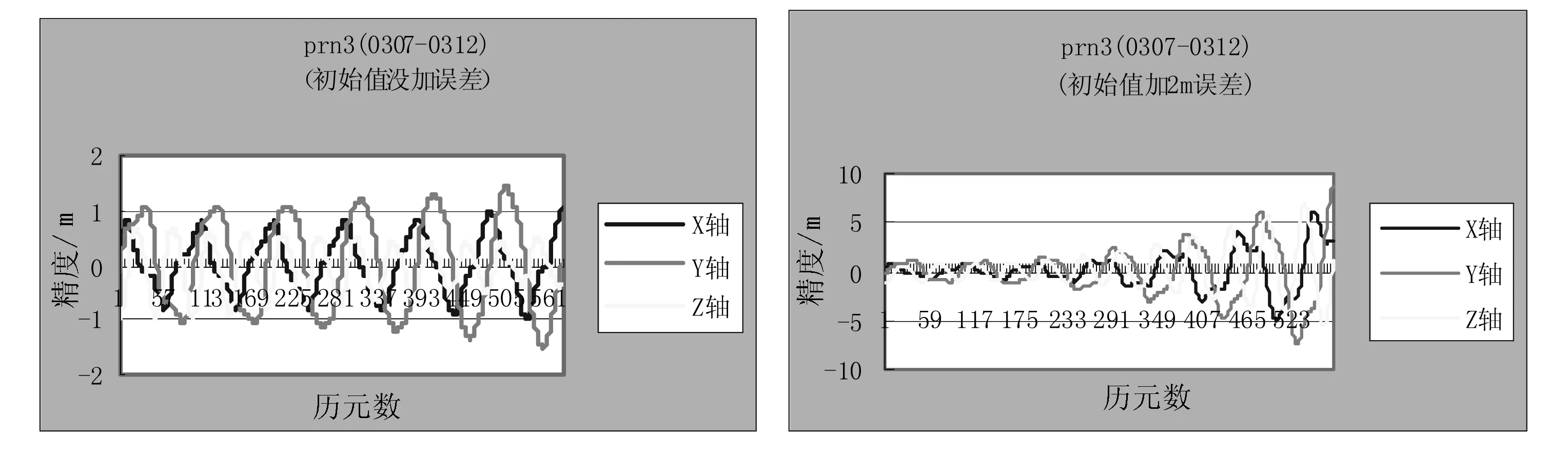
图2 初始值加误差前后的外推情况比较

表2不同方法求取卫星加速度的比较

历元(MJD)/各坐标轴用公式求取Collocation积分两种方法的差值(km/s2)53 162.001 770 832 8X0.109 865 347 224 5610.109 865 347 224 559-1.998 401 444 325 282E-015Y0.493 300 376 260 9370.493 300 376 260 938 1. 665 334 536 937 735E-016Z0.261 502 773 531 6570.261 502 773 531 655-1.609 823 385 706 477E-01553 162.002 812 499 9X0.104 665 012 917 0680.104 665 012 917 068-4.857 225 732 735 060E-016Y0.491 714 709 458 9210.491 714 709 458 921-2.220 446 049 250 313E-016Z0.266 703 327 879 2320.266 703 327 879 231-2.220 446 049 250 313E-016

4 结束语

详细讨论了GPS轨道仿真中初值的确定和轨道外推的方法，基于Collocation积分的方法不仅可以方便的求取仿真间隔内任意历元的卫星位置、速度和加速度，还能方便的求取仿真中用到的特殊量-加加速度。先用IGS精密星历数据评定轨道仿真的精度，试验数据表明，在外推5天的情况下，精度达到16 m以内以及同一颗卫星在不同日期外推精度不同主要是受初始精度的影响。再用两种不同方法(卫星受摄动运动公式和Collocation积分法)比较了卫星加速度的计算结果，实验表明Collocation积分方法更适用于GPS轨道仿真。

[1] 谭述森，卫星导航定位工程[M].北京：国防工业出版社，2010.

[2] 许其风．我国成功发射导航定位卫星[J].测绘信息与工程，2001.

[3] 葛榜军，廖春发．卫星应用现状与发展(上册)[M].北京：中国科学技术出版社，2001.

[4] 吴志忠.移动通信无线电波传播[M]. 北京：人民邮电出版社，2002.

[5] CHAKRAVARTHY V, NUNEZ A S, STEPHENS J P,etal. TDCS, OFDM, and MC-CDMA: a brief tutorial[J]. IEEE Radio Communications, 2005, 43 (9): S11-S16.

[6] ROBERTSs M L, TEMPLE M A. Transform domain communications: interference avoidance and acquisition capabilities[C]∥ National Aerospace and Electronics Conference， 2000:610-617.

[7] ROBERTS M L, TEMPLE M A, RAINES R A,etal. Initial acquisition performance of a transform domain communication system: modeling and simulation Results[C]// Proceedings of IEEE MILCOM,2000: 1119-1123.