利用改进的Kalman滤波算法进行GNSS单历元姿态测量

赵佩铭,张月超

(1.上海市政工程设计研究总院(集团)有限公司,上海200082;2.中国石油集团工程技术研究院,天津 300451)

0 引 言

单历元定位定姿的特征是仅利用当前观测历元的GPS观测数据,其前提是要有高精度的载波相位观测值[1-2]。在利用GPS观测值做单历元定位定姿解算中,无论是通过相位平滑伪距差分解算还是利用载波相位解算,传统的方法并未考虑载体前一历元时刻的姿态及其变化率对当前时刻姿态的影响,只利用当前时刻的历元数据求得最小二乘解,因此在解算结果的平滑性上并不理想;另外,在单历元定姿中容易受到噪声值的影响,使得解算结果出现较大跳变影响定姿结果的稳定性，综合来讲,现有的GPS定姿直接解算方法,大致存在以下几种缺陷:1)不具有抗差性;2)对运动载体而言,没有充分利用运动模型的信息;3)当一些历元的实际观测值少于必要观测数时,会出现无解的情况[3]。

Kalman滤波作为一种新的重要的最优估计理论已被广泛应用于各种测量数据的处理[4]。在Kalman滤波估计理论中引入了状态空间的概念,借助系统的状态转移方程根据前一时刻的状态估值和当前时刻的观测值递推估计新的状态估值[5]，与最小二乘法比较,Kalman滤波更适合于GPS动态定位数据处理[5]，在消除噪声影响方面,近几年基于Kalman滤波的抗差估计已有广泛的研究[6]。对于GPS单历元定姿数据中噪声值的影响,本文基于稳健估计理论在Kalman滤波方程的解算过程中加入抗差因子,以消除或减弱粗差或较大误差项的影响，在实际解算中验证了此方法的正确性,具有较好的应用效果。

1 姿态计算原理和方法

1.1 姿态解算中的坐标系

若能确定平台上不在同一直线上的三个点的精确相对位置,那么就能确定该平台的姿态[1]。在姿态测量中,表述一个运动载体的瞬时特征要涉及到两个独立的坐标系:载体坐标系和当地水平坐标系,通常利用表述两个坐标系关系的3个欧拉角描述载体在当地水平坐标系中的姿态[7]。GPS直接测量值是在WGS-84坐标系下的位置信息,WGS-84坐标系属于地心地固坐标系。

测站水平坐标系(LLS)即站心坐标系:以测站为原点,测站上的法线(或垂线)为Z轴方向,北方向为X轴,东方向为Y轴,建立坐标系[8]。

载体坐标系(BFS):一般将载体坐标系的原点与当地水平坐标系的原点重合,定义Y轴与载体运动方向的中心线重合,正向指向载体的运动方向,X轴垂直于Y轴并位于同一平面内,Z轴垂直于X,Y轴构成的平面成右手坐标系。

当地水平坐标系与载体坐标系之间的三个旋转角分别用y,p,r表示航向角,俯仰角和滚动角。如图1所示,假设12方向为参考方向,在计算姿态角时要首先将地固地心系下的坐标转换为以1号点为坐标原点的站心坐标,设2、3号点的站心坐标分别为(x2,y2,z2)和(x3,y3,z3),则有[1-3]:

航向角:

(1)

俯仰角:

(2)

翻滚角:

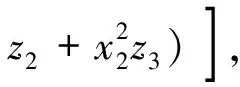
(3)

其中,S12,S13分别表示1、2点和1、3点间的距离。

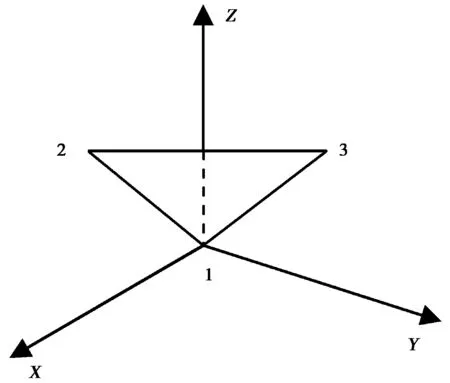
图1 站心坐标系中表示姿态角

1.2 GPS单历元定姿解算

一般的姿态测量系统的硬件采用多个天线共一个接收机的方式,显然两个天线之间的单差观测值中消除了与接收机和卫星相关的误差[5]。在这种情况下,使用单差观测值解算姿态角,其解的强度要比双差方法高。现有研究已经证明,主天线坐标误差在100 m时,其对定姿结果的影响仅为毫米级,因此利用伪距单点定位方式确定主天线位置可以满足定姿精度的要求[3]。假设现有1、2、3三个GPS天线,将天线1作为主天线,GPS观测值组成的双差观测方程为

(4)

式中：Δφ为双差相位观测量;R表示接收机与卫星间的几何距离;N为整周模糊度; 1,2表示接收机编号；i,j为卫星编号。采用双差观测值能够有效的消除接收机和卫星钟差,削弱电离层、对流层的影响。对于相位观测值而言,同时也使得模糊度具有整周特性,有利于后面的模糊度解算。

对式(4)做整理变换,得到误差方程式

(5)

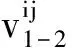
由观测数据计算得出载体在WGS-84坐标系下的基线向量值dXWGS-84,将空间坐标系下的基线向量转换到当地水平坐标系中[8]:

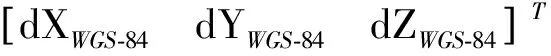
(6)

式中,B,L为主天线点的大地经纬度。

2 姿态滤波平滑及稳健参数估计

2.1 Kalman滤波在姿态解算中的应用

为了有效利用历元间的状态信息,同时要消除误差的影响,本文提出采用Kalman滤波进行姿态参数的抗差估计。在状态空间下的Kalman滤波的状态方程和观测方程为[9-11]

(7)

式中:Xk+1为系统状态向量;Lk+1为观测值;Φk+1为状态转移矩阵;Uk、Zk+1为非随机控制向量;Wk为系统动态噪声;Vk+1为观测误差;Υk+1、Ψk+1、Bk+1为相应的系数项,在一般系统中不考虑非随机控制量Uk和Zk+1,本文亦是如此。

假设系统具有随机统计特性

(8)

进行推导,得出Kalman滤波的递推解[4]为

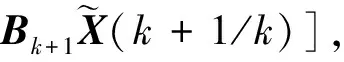
(9)

DX(k+1/k+1)= (E-Jk+1Bk+1)

DX(k+1/k)，

(10)

其中,滤波估计值为

(11)

其协方差阵

(12)

系统增益矩阵

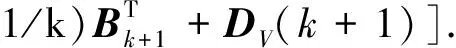
(13)

滤波解的另一种直接表达形式为

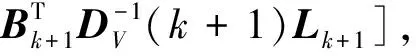
(14)

(15)

以系统的姿态角及其变化速率作为状态向量,即X=[yprvyvpvr]T,则其状态转移矩阵为

(16)

式中,Δt为前后历元时间间隔。

在姿态解算中,通常假定姿态角加速度为高斯白噪声,对各姿态角的系统噪声认为其方差为[3]

(17)

2.2 改进Kalman滤波稳健估计算法推导及程序实现

在2.1小节中论述的是经典Kalman滤波的基本过程及其如何应用在GNSS单历元姿态测量中。对于在计算过程中碰到可能出现的粗差问题,本文提出一种稳健Kalman滤波修正方法以期消除或削弱粗差对计算结果的影响。根据抗差M估计原理,引入降权因子γ,对于滤波计算过程中的新息残差向量:

(18)

结合Huber权函数,γ降权因子可由下式确定:

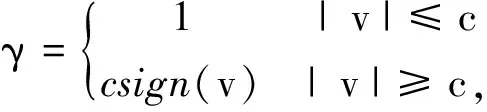
(19)

(20)

式中，c为预先设定的参数。引入单位权阵,则抗差Kalman滤波解为

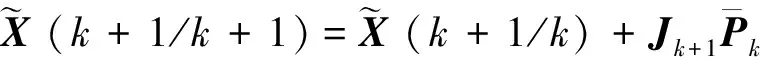
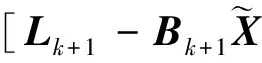
(k+1/k)],

(21)

(22)

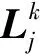
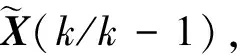
2)引入调节因子γ,设初始值为单位阵;

5)计算残差向量Vk,并判断其是否符合要求;

6)根据新息残差向量值,重新计算调节因子,由此新的调节因子γ,得到新的权阵,解算滤波值。

7)重复计算(2)到(6)步,直到残差向量收敛为止。

3 实验计算与分析

在建筑物顶架设载体,载体为三角框架结构,三个顶点上可以放置GPS接收机,中心点可以放置其他定姿仪器。实际数据采集时，在三个顶角上放置Leica GS15双频接收机,载体中心点上放置激光跟踪仪的6维定姿模块,载体底部放置IMU模块。3台GPS接收机进行同步观测,观测时的采样率设置为1 s,静置采集时间共20 min.

对姿态角进行直接解算,包括伪距解算和载波相位解算两种情况;其次,采用改进的稳健Kalman滤波算法解算,同样包括伪距解和载波相位解。两种方法的静态相位解算结果与跟踪仪定姿结果和IMU定姿结果相吻合。

另外,利用每一历元的观测值作虚拟动态定位,采用两种方法分别计算出每一历元的姿态参数。两种方法计算结果的误差统计表如表1所示。

从表1中的各姿态角平均值可以看出,无论是利用最小二乘方法还是利用改进的Kalman滤波方法,均能有效的解算出载体姿态角;通过比较最值可以看出改进Kalman滤波算法要比最小二乘算法的稳定性好。采用改进Kalman滤波算法的解算结果中消除掉了大部分的噪声值，使得定姿结果更趋于平稳；在出现粗差项时，改进Kalman滤波算法也具有很好的抗差性。

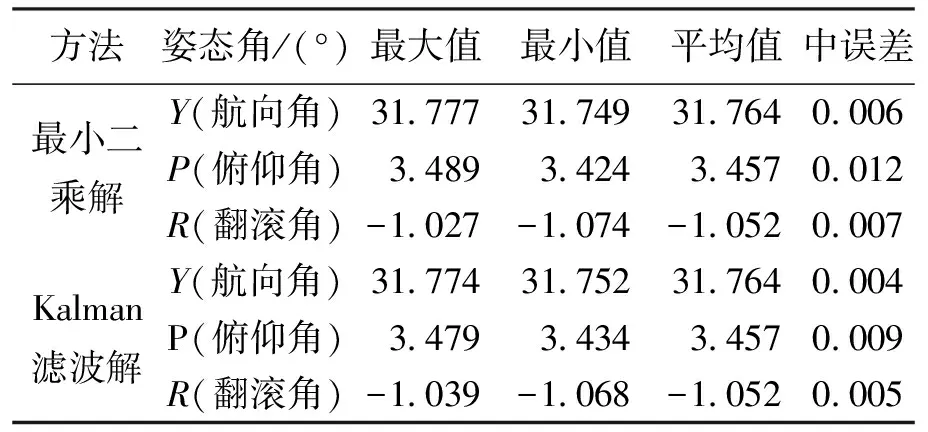
表1 姿态结果差值的统计分析

4 结束语

基于Kalman滤波的GPS定姿算法能够比较充分的利用前后历元间的载体姿态状态关系,提高定姿结果的平滑性和稳定性。本文提出的利用改进的Kalman滤波算法进行GNSS单历元姿态测量在抗差性上有了比较好的提高。通过对解算结果的统计分析及绘制出的折线图,可以看出:

1)在单历元动态定姿解算中,采用Kalman滤波进行姿态解算的解算结果要优于采用最小二乘间接平差的姿态角直接解算的结果;

2)对于出现的跳变数据或噪声项,Kalman滤波本身就具有一定的抵抗性,并且在加入抗差因子后,改进Kalman滤波算法能够较好的消除跳变值的影响。

如何更好的提高算法效率及更有效的解决单历元解算中模糊度解算问题是今后深入研究解决的问题。

[1]刘根友,欧吉坤.GPS单历元定向和测姿算法及其精度分析[J].武汉大学学报·信息科学版,2003,28(6):732-735.

[2]ZHEN D, KNEDLIK S, LOFFELD O,etal. A matlab toolbox for attitude determination with GPS multi-antenna systems[J].GPS Solut,2009,13(3):241-248.

[3]祁 芳.卡尔曼滤波算法在GPS非差相位精密单点定位中的应用[D].武汉：武汉大学测绘学院,2003.

[4]齐公玉,邱卫宁,花向红.卡尔曼滤波粗差修正方法应用[J].测绘工程,2010, 19 (2):50-52.

[5]WELCH G, BISHOP G. An introduction to Kalman filter[M]. ACM,INC,2001.

[6]张朝玉.卡尔曼滤波在多维AR序列建模中的应用[J].大地测量与地球动力学,2003(2):92-95.

[7]陈万通,秦红磊.一种新的GPS单频单历元定姿算法研究[J].上海航天,2012,29(3):11-14.