基于多普勒辅助的电离层残差探测与修复周跳改进方法

马 驰,李柏渝,刘文祥,王飞雪

(国防科学技术大学电子科学与工程学院卫星导航定位技术工程研究中心,湖南 长沙 410073)

0 引 言

卫星在空间的运行轨迹是一条平滑的曲线,因而卫星至接收机的距离观测值的变化是平缓而有规律的,而周跳将破坏这种规律性,使观测值产生一种系统性的粗差。周跳探测与修复的本质就是从载波相位观测值的时间序列中寻找可能存在的这种系统性粗差并加以改正。周跳产生的原因主要有三个方面:一是障碍物的遮挡造成卫星信号无法到达接收机天线,二是由于干扰或者多径的影响造成接收机处的卫星信号信噪比过低,三是接收机软件故障或者卫星信号振荡器故障。

传统的单频周跳探测方法有多项式拟合法[1]、高次差法[2],高次差法本质上与多项式拟合法是一致的,仅在目标动态变化较小时较为有效且精度不高;随着周跳技术不断发展,又出现了更加有效的多普勒积分法[3]、小波变换法[4];同时多频数据处理技术的发展促使精度更高的周跳探测方法产生,如电离层残差法[5]、M-W法(双频码相组合法)[6],电离层残差法是目前周跳探测与修复相对最准确的方法,可以准确探测到1周的小周跳,但当多个频点于同一历元发生周跳时,无法有效地进行周跳探测与修复。

本文充分研究电离层残差法与多普勒积分探测周跳的原理以及特点,提出了一种基于多普勒辅助的改进的电离层残差法来探测与修复周跳,并通过实验分析证明了该改进的方法有效解决了电离层残差法存在的上述问题,当多频点于同一历元发生周跳时,也能探测与修复小至1周的周跳,提高了电离层残差法探测与修复周跳的准确性与可靠性。

1 电离层残差法原理

卫星导航定位中接收机的载波相位观测方程为[7]

Tfi(tk))+fi(τr(tk)-τs(tk)),

(1)

式中:tk为观测历元时刻;fi为载波频率;φ(tk)为载波相位观测值;ρ(tk)为接收机与卫星之间的几何距离;N为载波相位整周模糊度;I(tk)为电离层延迟误差;T(tk)为对流层延迟误差;τr(tk)为接收机钟差;τs(tk)为卫星钟差。

由式(4)可得双频无几何关系载波相位组合观测值

φIE(tk) =λf1φf1(tk)-λf2φf2(tk)

=λf2Nf2-λf1Nf1+If2(tk)-If1(tk)

(2)

在相邻历元的无几何关系载波相位组合观测值之间作差,可得电离层残差

Δion(tk+1) =φIE(tk+1)-φIE(tk)

(3)

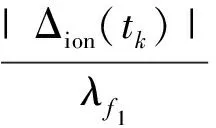
2 多普勒积分探测周跳原理

卫星与接收机之间存在着相对运动,导致接收机天线接收的卫星发射的载波频率附加了多普勒频移值。多普勒频移观测值与载波相位观测值具有如下关系

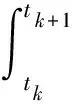
(4)

式中:φ(tk)为载波相位观测值;d(tk)为多普勒观测值;tk为观测历元时刻。

若在历元tk至tk+1间未发生周跳,则φ′(tk+1)与φ(tk+1)之间差值的绝对值(即多普勒残差,记为Δdopp(tk))应仅包含观测噪声的影响,其值应在一定范围之内

Δdopp(tk+1)=|φ′(tk+1)-φ(tk+1)|<δ，

(5)

式中,δ为门限值。由于多普勒观测值对周跳不敏感[7],若差值超出该门限,则可认为在历元tk至tk+1间发生了周跳,此时周跳的估值为多普勒残差值就近取整。

ΔN=[Δdopp(tk+1)]=[|φ′(tk+1)-φ(tk+1)|].

(6)

利用上述方法探测周跳,对各个频点上的载波相位观测值与多普勒观测值做相应处理,即使多频点同时发生周跳,也可以准确探测周跳发生的频点、位置及相应数值。

3 基于多普勒辅助的电离层残差法探测与修复周跳

由前两节的分析可知,多普勒积分法与电离层残差法有着很好的互补性,故提出一种综合利用多普勒积分与电离层残差的方法来探测与修复周跳。由于多普勒积分法能识别周跳发生的频点,于是用来与电离层残差法进行互补,形成综合策略。

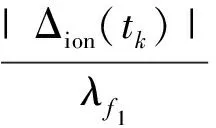
图1 周跳探测与修复流程图

4 实验与分析

为验证本方法,研究了2014年4月2日于长沙采集的一组BDS双频数据,两频点为B1与B3,故f1=152.6f0、f2=124f0,其中f0=10.23 MHz,设门限值ε=0.02,δ=0.4.经验证,如图2所示,整个观测时段的电离层残差平均值为1.6497×10-4<0.02,则该组数据无周跳。

4.1 常规电离层残差法性能研究实验

人为地在B1频点第200历元加入1周的周跳,在B3频点第500历元加入1周的周跳。如图3所示,对整个观测时段进行电离层残差分析。在第200历元处,电离层残差值|Δion(200)|=0.1923>0.02;在第500历元处,电离层残差值|Δion(500)|=0.2398>0.02.可知,观测数据在第200历元和第500历元发生周跳。

图2 原始数据的电离层残差图

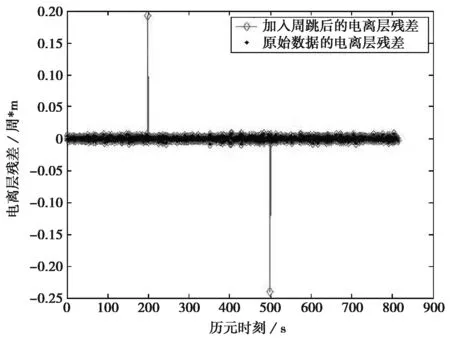
图3 加入周跳后的电离层残差图

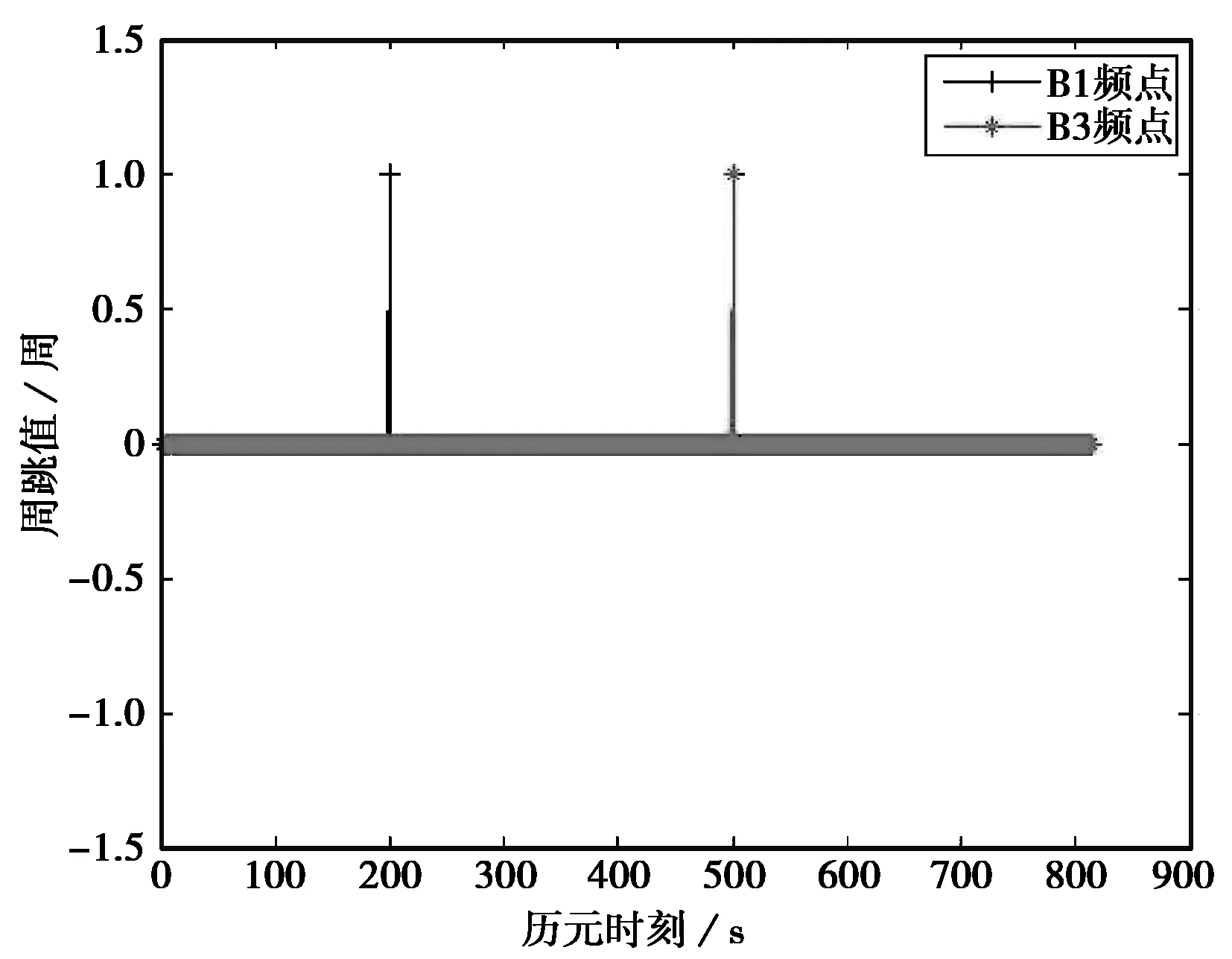
图4 周跳计算结果

如图5所示,对观测数据进行周跳修复后的整个观测时段上的电离层残差平均值为1.6497×10-4<0.02,可知常规电离层残差法可以准确而可靠地探测并修复不同历元上发生的周跳。

图5 进行周跳修复后的电离层残差图

4.2 常规与改进的电离层残差法性能比对实验

图6 加入周跳后的电离层残差图

在该种情况下,本文采用的基于多普勒辅助的改进的电离层残差法,运用多普勒积分进行周跳的频点以及大小探测。如图7所示,对整个观测时段进行多普勒残差分析,在第300历元处的B1频点的多普勒残差值Δdopp(300)=0.9225>0.4,则B1频点上发生周跳,且周跳值ΔN=[|Δdopp(300)|]=1;在第300历元处的B3频点的多普勒残差值Δdopp(300)=0.9680>0.4,则B3频点上发生周跳,且周跳值ΔN=[|Δdopp(300)|]=1.计算结果如图8所示,B1频点与B3频点均于第300历元发生1周周跳。

图7 各频点的多普勒残差图

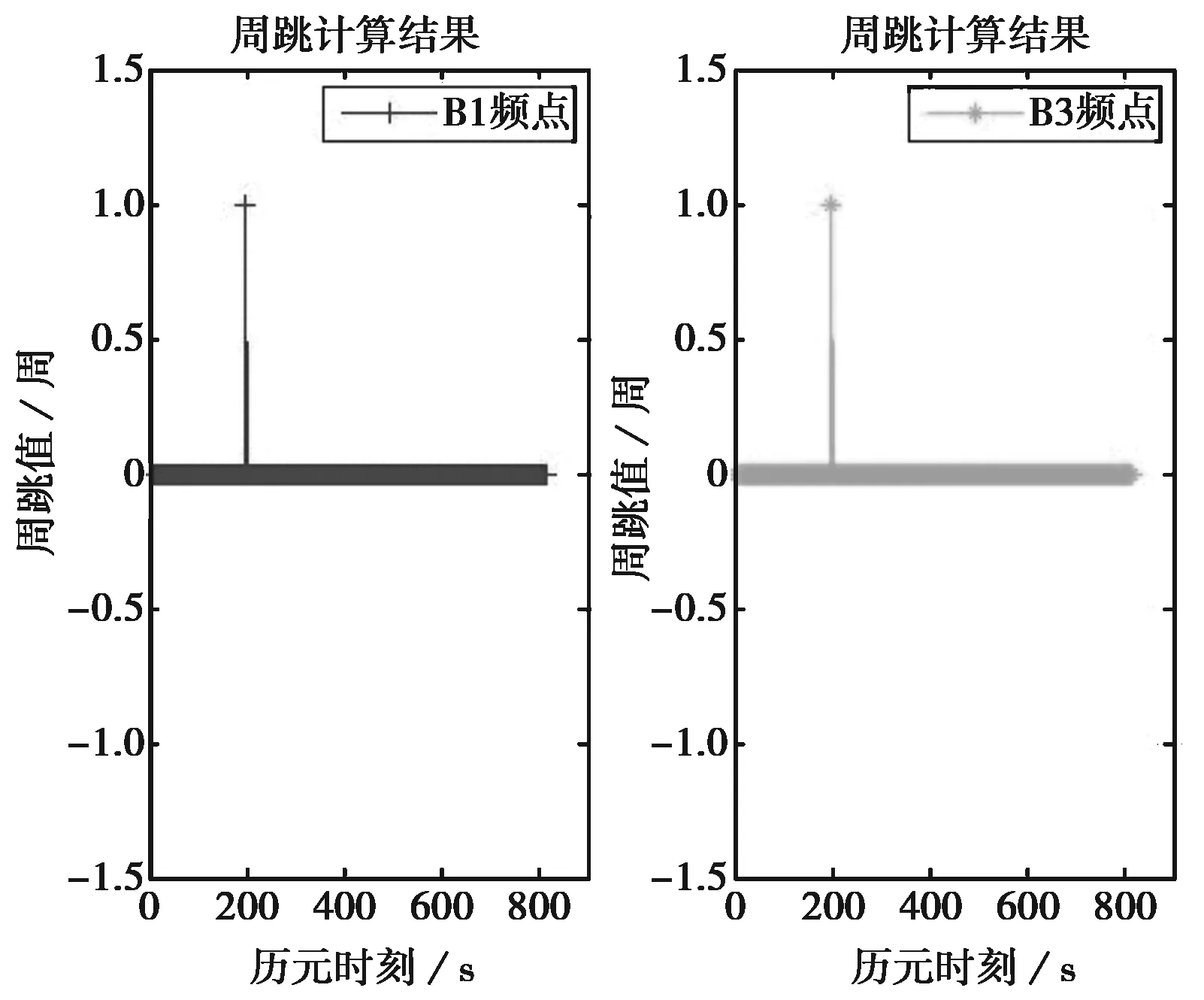
图8 周跳计算结果图

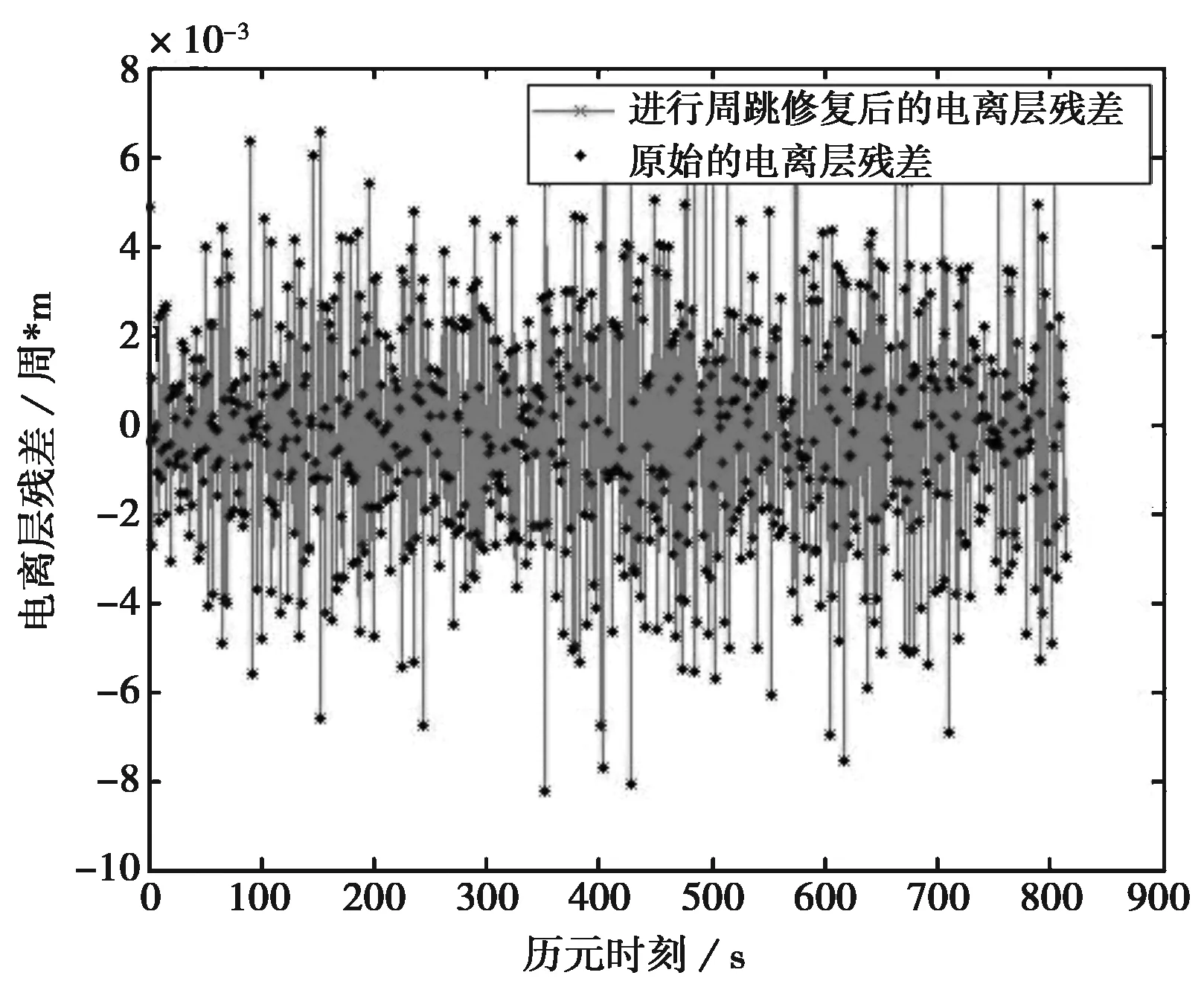
图9 进行周跳修复后的电离层残差图

如图9所示,对观测数据进行周跳修复后的整个观测时段上的电离层残差平均值为1.6497×10-4<0.02,可知当同一历元不同频点发生周跳时,改进的电离层残差法仍可以准确而可靠地探测并修复低至1周的小周跳。

5 结束语

本文分析研究了典型周跳探测与修复方法中的电离层残差法以及多普勒积分探测周跳的原理,提出一种基于多普勒辅助的改进的电离层残差法,并通过BDS双频实测与仿真数据对该方法进行了验证,实验结果分析表明：改进后的方法有效解决了当同一历元多个频点发生周跳时,常规电离层残差法不能准确探测与修复周跳的问题,可以准确而可靠地探测并修复低至1周的小周跳。

[1]李 明, 高星伟, 徐爱功. 一种改进的周跳多项式拟合方法[J]. 测绘科学, 2008, 33(4): 82-83.

[2]王爱生, 欧吉坤, 徐爱功. 周跳在高阶差分中的时序

特征及精确估计[J]. 大地测量与地球动力学, 2008, 28(5): 59-64.

[3]常志巧, 郝金明, 李俊义. 利用多普勒观测检测周跳和粗差[J]. 测绘通报, 2008(3): 28-30.

[4]蔡昌盛, 高井祥. GPS周跳探测及修复的小波变换法[J]. 武汉大学学报, 2007, 32(1): 39-42.

[5]LIU Zhizhao. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver[J]. Journal of Geodesy, 2011(85): 171-183.

[6]KIM D, LANGLEY R B. Instantaneous real time cycle-slip correction of dual-frequency GPS data[C]//International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation, Banff, Alberta, Canada, 2001.

[7]李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.

[8]严 悦. 电离层残差法探测与修复周跳特性分析[J]. 地理空间信息, 2010, 8(4): 118-120.