基于模糊神经网络算法的机器人路径规划研究

姚毅, 陈光建, 贾金玲

(四川理工学院b.计算机学院;a.自动化与电子信息学院, 四川自贡643000)

基于模糊神经网络算法的机器人路径规划研究

姚毅a, 陈光建b, 贾金玲b

(四川理工学院b.计算机学院;a.自动化与电子信息学院, 四川自贡643000)

路径规划是移动机器人研究的关键技术之一。在研究模糊理论和神经网络的基础上，提出了一种新的算法，即模糊神经网络。模糊神经网络既可以像神经网络那样并行处理、自行学习，又可以像模糊理论处理模糊信息、完成模糊推理功能。采用模糊神经网络来对移动机器人的路径进行规划，充分发挥模糊理论和神经网络的各自优势，从而获得从起始点到目标点的最优路径。在环境信息完全未知且静态的情况下进行了仿真实验，结果表明：该算法效率高、收敛速度快，有效提高了移动机器人的智能化水平。

移动机器人；路径规划；模糊理论；神经网络

引言

目前，机器人的发展趋势是高度智能化，而路径规划又是评定机器人智能化的重要指标。所谓路径规划技术就是当机器人在前进过程中当遇到障碍物无法前进时，需要重新寻找一条路径到达终点。新找的一条路径不仅能使机器人绕过障碍物，而且要用时最短，选择的距离最科学。障碍物的大小，距离机器人的距离都直接影响到机器人的路径规划。随着机器人技术向人工智能化方向的发展，对机器人的路径规划提出了越来越高的要求。神经网络和模糊算法在人工智能方面都表现了各自的优越性，但也存在许多弊端。神经网络虽然有很好的学习功能及鲁棒性，但是它不适合对已经存在的规律性知识的表达，对已有先验知识不能很好的利用。模糊逻辑能将通常不能用数学方法精确处理的问题用模糊的方法来综合判断，但需要全面的先验知识，来构成推理规则和模糊表。在路径规划中，通过模糊算法和神经网络的有机结合可以很好地综合各自的优点，使规划的方式更灵活，规划的效果更优越。

本文在研究了模糊逻辑算法和神经网络算法的基础上，提出了模糊神经网络算法，并应用于移动机器人的路径规划，最后通过了仿真验证该算法切实可行的。

1 模糊神经网络

1.1神经网络

人工神经网络(Artificial Neural Networks，简称ANN)是一种模拟人类大脑的思维能力，通过大量的模拟神经元来实现非线性算法功能的一种网络。它与人脑神经系统处理信息的过程类似，都具有学习和自适应功能，不同在于其理论基础是数学网络拓扑，用神经网络自身结构表达输入输出关系，使网络具有非线性映射的功能对信息进行并行处理。人工神经网络主要特点是非线性、能够并行处理信息的网络，且具有学习功能、容错性、信息分布式存储功能及鲁棒性。人工神经网络的学习规则主要有误差纠正学习、竞争学习、Hebb学习等。

1.2模糊理论

模糊理论(Fuzzy Theory)是指用到了模糊集合的基本概念或连续隶属度函数的理论。通过研究发现，模糊逻辑和神经网络这两种技术各有所长且具有互补性，因此利用一定的技术将模糊逻辑与神经网络适当地结合起来，形成一种新的结构，此结构吸取了两者的长处，且在不失原有特点的基础上又有自己的特性，是比单独的神经网络或单独的模糊系统性能更好的系统。对于移动机器人路径规划这样复杂的系统，模糊神经控制技术有其巨大的优势。

1.3模糊系统和神经网络的融合方式

将神经网络和模糊逻辑采用一定的手段结合起来形成了一种新结构的技术，叫神经模糊技术。它们的融合主要有神经网络和模糊系统集成[1]、模糊逻辑增强型的神经网络、模糊神经网络三种方式[2-4]。

本文研究的是模糊神经网络。模糊神经网络其实就是在传统的神经网络中加入了一些模糊成分而形成的。它既可以像神经网络那样并行处理、自行学习，又可以像模糊理论处理模糊信息、完成模糊推理功能。根据在神经网络中加入的模糊成分不同，又可以将模糊神经网络分成不同类型。模糊神经网络在保持原有功能的基础上又有自身的特点。

2 模糊神经网络的结构及学习算法

2.1模糊神经网络的结构

模糊推理中的关键问题就是隶属度函数和模糊规则的确定，而基于神经网络的模糊控制器将它们归结为神经网络参数和结构的训练。有学者提出了基于Takagi-Sugeno模型(简称T-S模型)的模糊神经网络，本文用变结构神经网络来实现基于T-S的模糊推理[5-9]。

模糊系统的输出量为每条规则的输出量的加权平均，即：

(1)

将多个单输出系统采用一定技术组合起来就形成了一个多输出系统。现代技术中可以用来实现上述模糊推理过程的典型方法就是神经网络。

2.2模糊神经网络的学习算法

模糊神经网络的学习包含两个步骤：

第一，参数初调及结构训练。根据经验确定网络参数初值，构造训练样本对，进行参数初始学习；然后根据如下规则进行变结构：对于与某个输出相对应的某个结点j，若与其相连的权均小于某域值，则删除该结点j。若对于所有的输出，其对应的结点j都被删除，则删除结点j。这表明第j条规则不存在，从而可以实现规则库的精炼[2]。

第二，进一步进行参数调整。在经过前面的训练调整后，其网络结构已经比较成熟，在此基础之上，让参数进行再学习。

从本质上来讲，由于模糊神经网络与BP网络的结构非常类似，因此，其参数学习完全可以借用BP网络的误差反传算法[10-11]。按照T-S模糊系统模型建立了模糊神经网络，该网络中的所有结点及相关参数都分别与模糊系统的隶属函数或者是推理过程对应。该网络中的参数值随系统的模糊或定性的知识都是可以根据需要确定的，因为神经网络是一个黑箱子，参数值要随机选取；另外，用较短的时间收敛到要求的输入输出关系，也是模糊神经网络的一个优点所在。由于它具有神经网络的结构，因此，可以实现规则及参数的自学习，与单纯的模糊逻辑系统相比，这也是它的优势所在。

3 机器人对环境的感知

机器人对环境的外部感知采用的是多传感器信息融合模型，具体结构如图1所示。

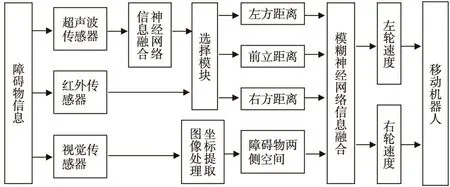
图1 机器人多传感器信息融合模型框图

实现它的核心硬件是智能机器人传感器交互模块，该模块通过串行口和I2C总线配置各个传感器，包括超声波、红外，摄像头；通过I2C总线连接六组超声波测距传感器和四组红外测距传感器获取机器人周围障碍物信息数据，并利用多传感器信息融合准确定位障碍物以便机器人实现避障和为返回做准备。用超声波传感器和红外传感器完成障碍物距离的测量，用视觉传感器完成障碍物边缘和位置信息的提取。在对障碍物距离的测量过程中，采用超声波传感器测距为主，红外传感器为辅，红外传感器主要用来弥补超声波传感器的一些缺陷，作为紧急避障来使用。

具体的原则为：对CCD摄像头采集到的视觉信息，按照数字图像处理的方法检测到障碍物的边缘，再利用分区扫描的办法获得障碍物边缘的像素坐标，最后得到障碍物两侧空间的大小，归一化处理后作为模糊神经网络输入[12]。

机器人在作业时主要靠传感器获得的外部障碍物信息以及自身所处的状态来决定下一步该怎样运动。机器人获得相关数据通后输入计算模块，通过计算得到合理的运动轨迹避开障碍物，且在避开障碍物后，能返回到设定运动路线上继续前进。

4 模糊神经网络的训练

为了减少模糊神经网络的训练时间，在此采用了离线训练[7,13]，其流程如图2所示。

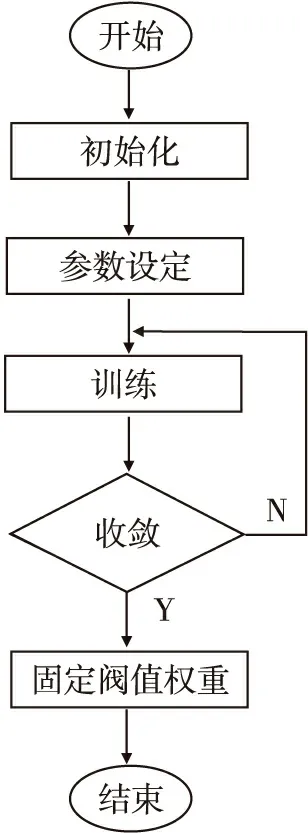
图2 模糊神经网络训练流程图

根据离线训练网络的参数和结构，把已建立的模糊控制规则作为模糊神经网络控制器的训练样本来训练网络。在训练好网络之后，模糊神经网络控制器就可以对移动机器人的局部运动进行规划，通过CCD摄像机、红外和超声波传感器来获取障碍物信息，从而实现对移动机器人的实时控制。

经过训练以后，隶属度函数变得很平缓，即机器人运行比较平稳；当障碍物距离机器人较近时，机器人会实时灵敏的做出相应的操作；当距离较远时，机器人具有较强的鲁棒性控制自己的运动。由此可知：经过训练，机器人的避障功能得到增强，用于输入变量的隶属度函数由于得到有效的优化而更适用于机器人的避障。

5 仿真结果

本仿真实验是在环境信息完全未知且静态的情况下进行的。在仿真实验中，一些外界信息都是通过计算得到的，但是在实际情况中，机器人作业环境的外部信息包括温度、湿度、障碍物分布情况等都是由传感器获得的。为了简化实验，在具体操作的时候，将外界信息理想化(比如将障碍物的形状用圆形来表示)。最后，分别给出了在同样的环境下障碍物多和障碍物少的路径图的两种仿真结果，其中移动机器人的起始点均为原点。图3是障碍物分布较密集的时候的路径轨迹,图4是障碍物分布较疏散的情况下的机器人仿真路径。

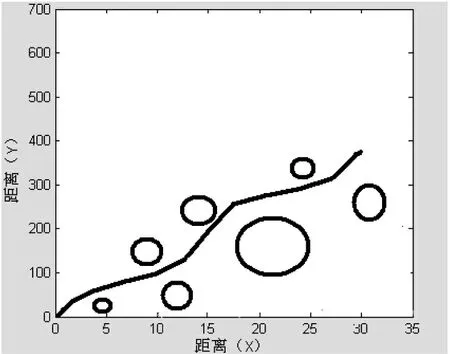
图3 障碍物(圆形)较多时的路径规划仿真图

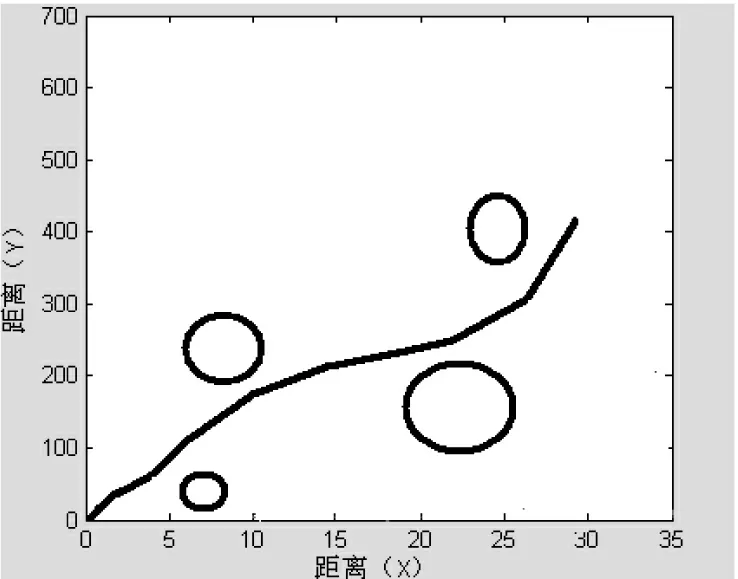
图4 障碍物(圆形)较少时的路径规划仿真图

通过以上仿真结果可以得出，采样时间的长短和转角度数的选择对机器人路径规划有相当重要的影响。仿真结果显示采样时间较短时，机器人在障碍物间就会不停地转向甚至在某些点会打转进而发生死锁现象；但当采样时间比较长时，机器人又会很容易和障碍物发生碰撞，当障碍物较小时机器人还会冲进障碍物区域。本文进行了多次试验，得到一组能满足大多数情况的采样时间和转角度数的组合：采样时间0.1秒，转角度数为5度。由仿真图可知，机器人可以比较顺利地完成路径规划，说明采用模糊神经网络算法是可行的。

6 结束语

本文以已有的机器人雏形为研究对象，针对未知环境下移动机器人路径规划问题开展研究。在对神经网络和模糊理论进行分析对比的基础上，将两者有机地结合到了一起，构建了在静态未知环境下用于路径规划的模糊神经网络，并提出了相应的方法。采用模糊神经网络对移动机器人的路径进行规划，从而获得从起始点到目标点的最优路径。该算法能够有效提高移动机器人的智能化水平。

[1] 许 亮.基于模糊神经网络的AUV路径规划技术[D].青岛:中国海洋大学,2007.

[2] 郑洪涛,李玉榕,乔 斌,等.基于模糊神经网络开关磁阻电动机转矩观测[J].仪器仪表学报,2002,23(4):351-353,360.

[3] 盖庆书,白 雪.基于神经网络模型的信息融合技术[J].华北水利水电学院学报,2009(1):25-27.

[4] 丛 爽,戴 宜.递归神经网络的结构研究[J].计算机应用,2004,24(8):18-21.

[5] 周 杰.含扩散项时滞模糊Cohen-Grossberg神经网络的指数稳定性[J].四川理工学院学报:自然科学版, 2010,23(3):270-274.

[6] 张寒松,贾瑞清.基于实际函数的机器人模糊神经网络路径规划[J].矿山机械,2010,38(14):44-48.

[7] 李贻斌,李彩虹,宋 勇.基于模糊神经网络的移动机器人自适应行为设计[J].山东大学学报:工学版,2010(2):28-33.

[8] 刘 毅.移动机器人路径规划中的仿真研究[J].计算机仿真,2011(6):227-230.

[9] 钱 夔,宋爱国,章华涛,等.基于自适应模糊神经网络的机器人路径规划方法[J].东南大学学报:自然科学版,2012(4):637-642.

[10] 李瑞峰,张 超,黄 超,等.清扫机器人路径规划的研究[J].机械设计与制造,2012(12):160-162.

[11] 郜园园,朱凡,宋洪军.进化操作行为学习模型及在移动机器人避障上的应用[J].计算机应用, 2013(8):2283-2288.

[12] 王华秋.自组织模糊神经网络的内模控制研究与应用[J].计算机仿真,2014(4):343-346.

[13] 张万绪,张向兰,李 莹.基于改进粒子群算法的智能机器人路径规划[J].计算机应用,2014(2):510-513.

Study on the Robot Path Planning Based on Fuzzy Neural Network Algorithm

YAOYia,CHENGuangjianb,JIAJinlingb

(a.School of Automation and Electronic Information; b.School of Computer Science, Sichuan University of
Science & Engineering, Zigong 643000, China)

Path planning is one of the key technologies for mobile robot researches. Based on the study of fuzzy theory and neural network, a new algorithm namely fuzzy neural network is proposed. Fuzzy neural network-FNN can not only perform parallel processing and self learning, as what NNs can do, but also process fuzzy information and perform fuzzy reasoning, as what fuzzy theory can do. The fuzzy neural network-FNN is used for designing routes of mobile robots, and respective advantages of fuzzy theory and NNs are fully utilized, then the optimum route from start point to object point is obtained. In conditions where environmental information is unknown and static, simulation experiment is conducted and the results indicate that this algorithm is efficient and has fast convergence rate, which helps to improve the intelligence level of mobile robots in an efficient way.

mobile robot; path planning; fuzzy theory; neural network

2014-08-01

人工智能四川省重点实验室基金项目(2014RYY01;2014RYY03);企业信息化与物联网测控技术四川省高校重点实验室基金项目(2013WZY02);四川理工学院校级培育科研项目(2012PY21;2013PY06)

姚 毅(1961-),男,四川自贡人,教授,硕士,主要从事信号检测与智能信息处理方面的研究,(E-mail)yaoyi@suse.edu.cn 陈光建(1979-),男,四川自贡人,副教授,硕士,主要从事计算机应用方面的研究,(E-mail)guangjian224@126.com;

1673-1549(2014)06-0030-04

10.11863/j.suse.2014.06.08

TP242

A