级联型多电平逆变器最小总谐波失真阶梯调制策略研究

李素非1，李国杰1，翟登辉2，王卫星2



级联型多电平逆变器最小总谐波失真阶梯调制策略研究

李素非，李国杰，翟登辉，王卫星

(1.电力传输与功率变换控制教育部重点实验室，上海交通大学电气工程系，上海 200240；2.许继电气股份有限公司，河南 许昌 461000)

为了降低级联型多电平逆变器的输出电压谐波分量，提出了一种新颖的基于KKT条件最优化方法的阶梯调制策略。利用KKT条件法，经过严格的数学推导，得到相应的导通角计算方法,所提出的阶梯调制策略能够在任意调制系数下最小化阶梯波输出的总谐波失真（THD）。另外利用牛顿-拉普逊迭代法来求取上述导通角计算中的关键参数。为了克服牛顿—拉普逊迭代法计算速度慢的缺点，提出了幂函数逼近法来简化计算复杂度。最后，对上述方法进行了仿真分析，得到了固定和可变调制系数下的级联逆变器输出电压波形和其频谱分布。仿真结果证实了调制策略的有效性。

级联型多电平逆变器；总谐波失真；阶梯调制；KKT条件法；函数逼近

0 引言

级联型逆变器在中/高功率等级的系统的中有广泛的应用。根据开关频率，可以将级联型逆变器的调制分为高频调制和低频调制。常见的高频调制策略有正弦载波调制（SPWM）、特定谐波消除脉宽调制（SHEPWM）空间电压矢量调制（SVPWM）。相对于高频调制策略而言，低频阶梯调制能减小开关损耗和器件的开关应力，延长其使用寿命，提高系统效率。

在阶梯调制中，各电平导通角的计算是一个研究热点。导通角计算方法包括选择谐波消去法（SHE）、等面积法、最小面积差法以及最小THD法。SHE法的目的是消去电压输出波形中的低次谐波，由于需要解多元非线性超越方程组，它的计算非常复杂。等面积法要求在每一个特定的时间区间内，参考正弦电压和阶梯调制波积分相同，但是它没有优化谐波失真，可能带来电压基频幅值失真。最小面积差法的主要目标是在每一个电平上，参考正弦电压和阶梯电压之差的积分最小，它同样会引入电压基波幅值失真。

总谐波失真是衡量逆变器输出波形质量的重要参数，本文主要研究最小化阶梯波调制中总谐波失真的方法。文献[26]采用Levenberg-Marquardt迭代法计算导通角，文献[27]提出粒子群优化算法，这些方法时间复杂度高，在线实现困难；同时，要求电压基频幅值不能随时间改变，且忽略高次谐波的影响，因而并不是严格数学意义下的最优解法。如果基频电压幅值是可变的，则需要离线解出对应于不同基频幅值下各电平的导通角，运行时通过查表得到各电平导通角。查表法虽然能降低计算复杂度，但精度和分辨率较低，并占用大量存储容量。有学者提出一种最小化总谐波失真的解析方法，能在线计算导通角，但仅优化了最多电平数量下的导通角，没有考虑较少电平数量下的限制条件，基频电压幅值也被限定在一定范围内；当电平数量多时利用牛顿—拉普逊迭代法，计算复杂。

本文利用KKT条件法，提出了一种在大范围基频电压下最小化阶梯波总谐波失真的在线计算方法，并利用函数逼近的方法简化计算过程。

1 级联型逆变器阶梯波调制简述

H桥级联型逆变器的拓扑结构如图1所示。它由个模块组成，每个模块有一个直流电压源，以及由四个开关器件及反并联二极管构成的H桥。

在图1中，对于第个模块来说，它的直流电压源是，输出电压为。当和导通，和关断时，；当和导通，和关断时，；当和导通，和关断时，。所以

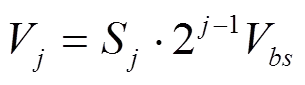
其中，

总输出电压为

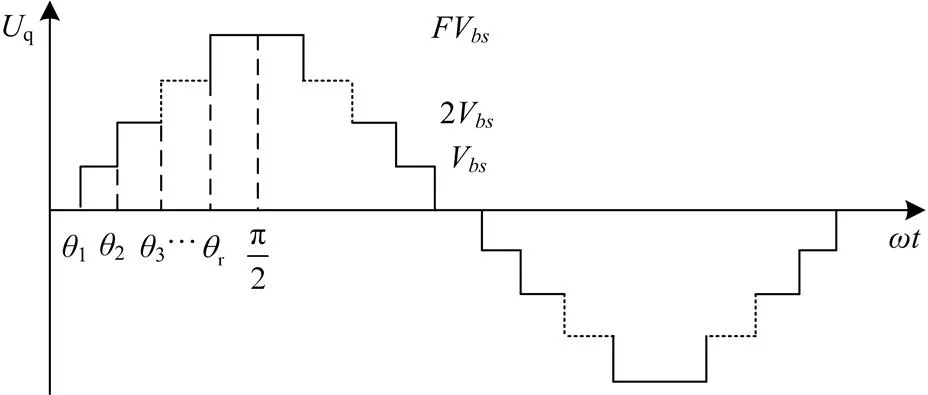
图2阶梯调制输出电压波形

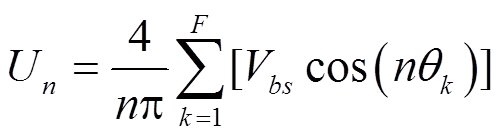
其中是奇数，偶次谐波为零。定义调制系数为

(4)

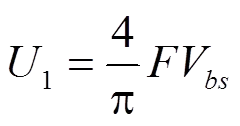
调制系数的范围为

(6)

总谐波失真定义为

根据帕斯瓦尔定理，有

(8)

将式（8）代入式（7）得

2 总谐波失真最小化方法

本节利用KKT条件法推导最小化总谐波失真的导通角计算方法。目标是在特定的调制系数下，求得一组导通角，使得式（9）中的总谐波失真最小。不失一般性，设，最高电平数为，在图1中。它等价于以下最优化问题：

(11)

(12)

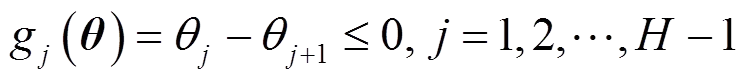
(14)

(16)

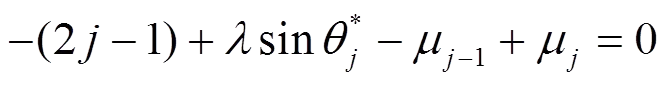
(19)

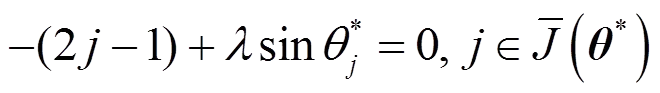
所以

(21)

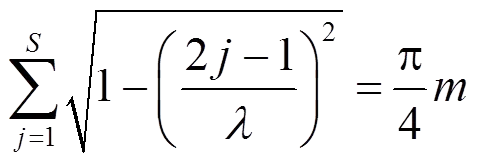
(23)

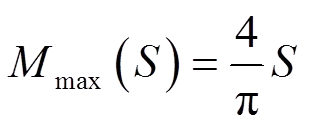
表1和

Table 1 and

Table 1 and

S 101.273 2 21.200 42.546 5 32.266 13.819 7 43.301 65.093 0 54.324 76.366 2 65.341 37.639 4 76.353 98.912 7 87.363 910.185 9 98.372 111.459 2 109.378 912.732 4 1110.384 814.005 6 1211.389 915.278 9 1312.394 416.552 1 1413.398 417.825 4 1514.401 919.098 6 1615.405 120.371 8

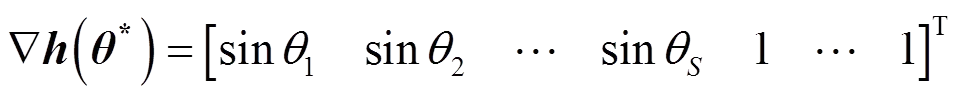
(26)

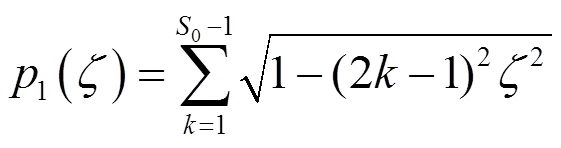
(29)

(30)

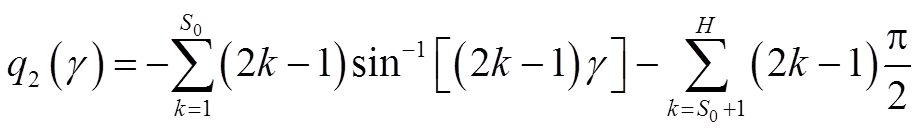
(32)

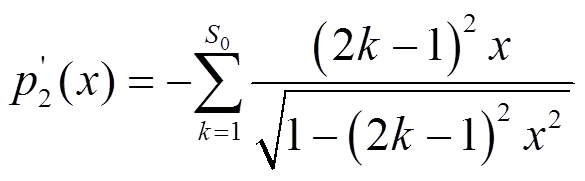
(34)

(35)

(37)

(38)

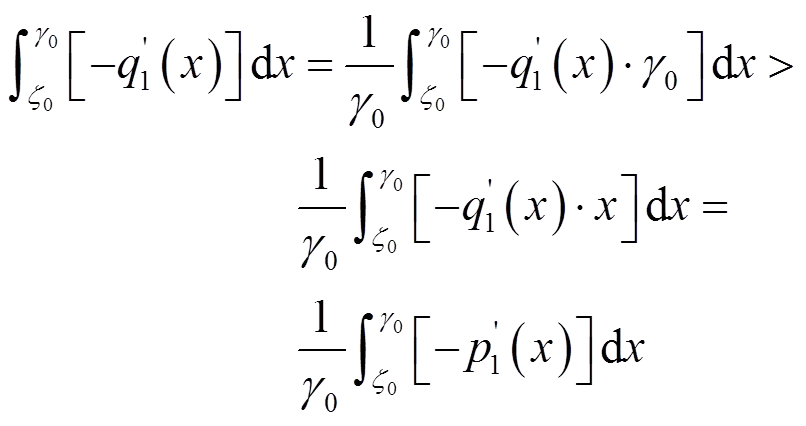
(40)

根据式（34），不等式（39）和式（40）的右侧相等。所以且。得证。

这样就得到了总谐波失真最小化的导通角计算方法。具体步骤如下：

4）根据式（21）计算各导通角的正弦，如果超过了1，令其为1。

3.1牛顿—拉普逊迭代法

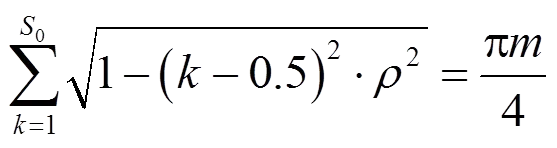
(42)

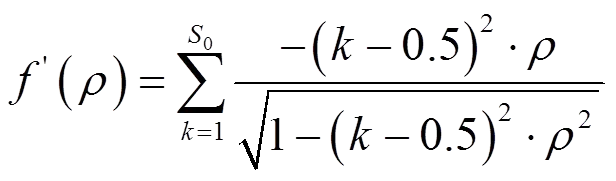
(44)

在实际系统中，调制系数是时变的，且在部分情况下它的变化比较连续。如果仍然在每一时刻都选取初始值，会增加迭代次数，占用计算资源。假设第时刻的第次迭代所计算的参数值为，第时刻迭代次后满足，且第时刻的阶梯级数为。则第时刻的参数初值按照以下方法求出：

下面讨论牛顿—拉普逊法的计算复杂度。这里仅包含迭代计算参数的算法复杂度，不考虑加减运算所消耗的时间，仅考虑乘法、除法、开方和反三角函数运算的时间。各，和的值已存储在微处理器或DSP芯片中。的值在对应于当前时刻的迭代开始前计算。对于当前时刻的各次迭代，根据式（42）和式（43），时间复杂度为

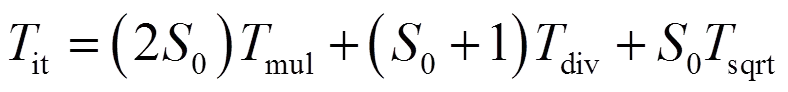
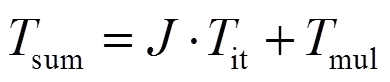
3.2幂函数逼近法

为节约运算资源，提升运算速度，并克服牛顿—拉普逊法的缺点，本文提出了幂函数逼近法。阶梯级数可以表示为调制系数的函数，即

(48)

3.2.1 选定拟合点集

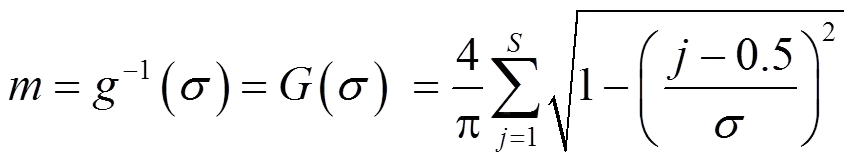
(50)

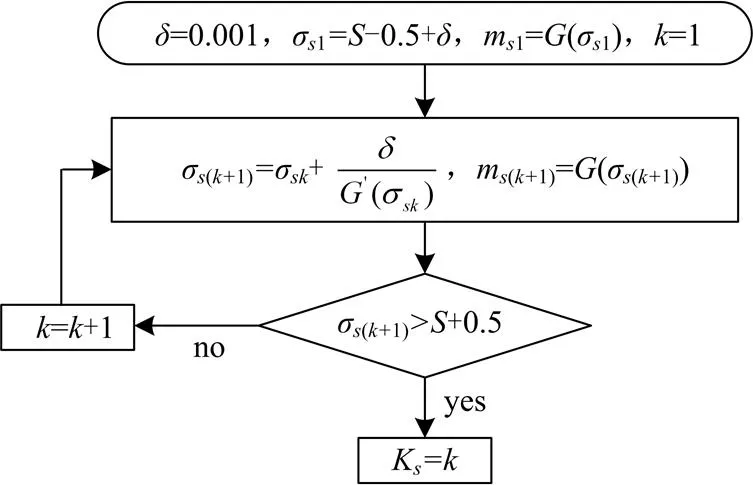
图3求取拟合点集的流程图

3.2.2 近似幂函数的求取

(52)

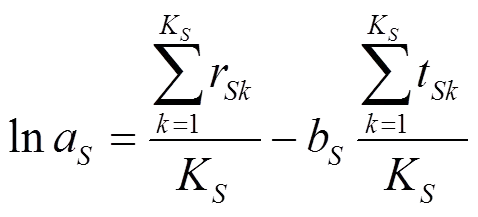
将式（52）和式（53）代入式（48）中就得到了近似的幂函数。为了评价近似函数的精度，分别定义对应于的相关系数和标准拟合误差为

(54)

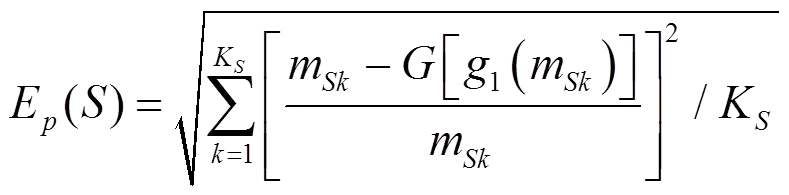
相应的近似幂函数系数和拟合精度结果如表2所示。

表2拟合结果

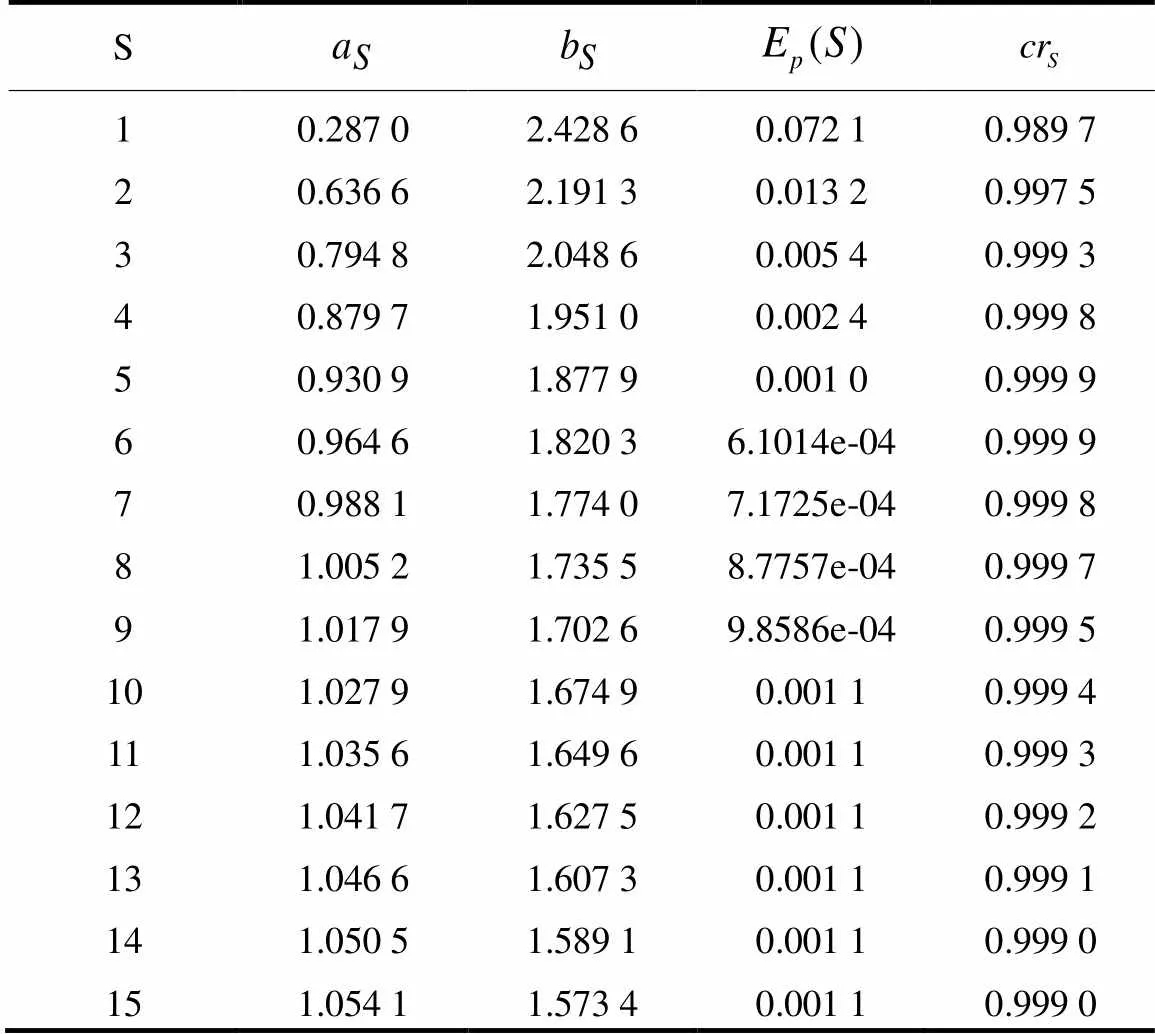
Table 2 Fitting results

调制系数的拟合误差如图4所示。调制系数的误差会导致基波幅值失真。

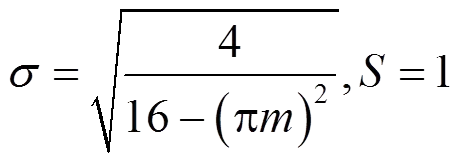
根据式（48），幂函数逼近法当前时刻的总时间复杂度为

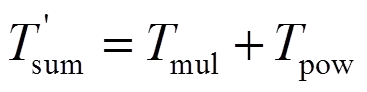
比较式（57）和式（46），可以发现幂函数逼近法的计算时间复杂度相对于牛顿—拉普逊法显著减少，并且不受阶梯级数、迭代次数的影响。为进一步节约计算资源，这里规定在第时刻，若，不再用式（48）计算对应于的参数的值，而是直接使用对应于的参数的值；否则需根据式（48）计算对应于的参数的值，并令，。其中为选定的误差阈值。目前的微处理器或DSP芯片能够胜任这些运算。

4 仿真结果

图5当时的输出电压及其各次谐波含量

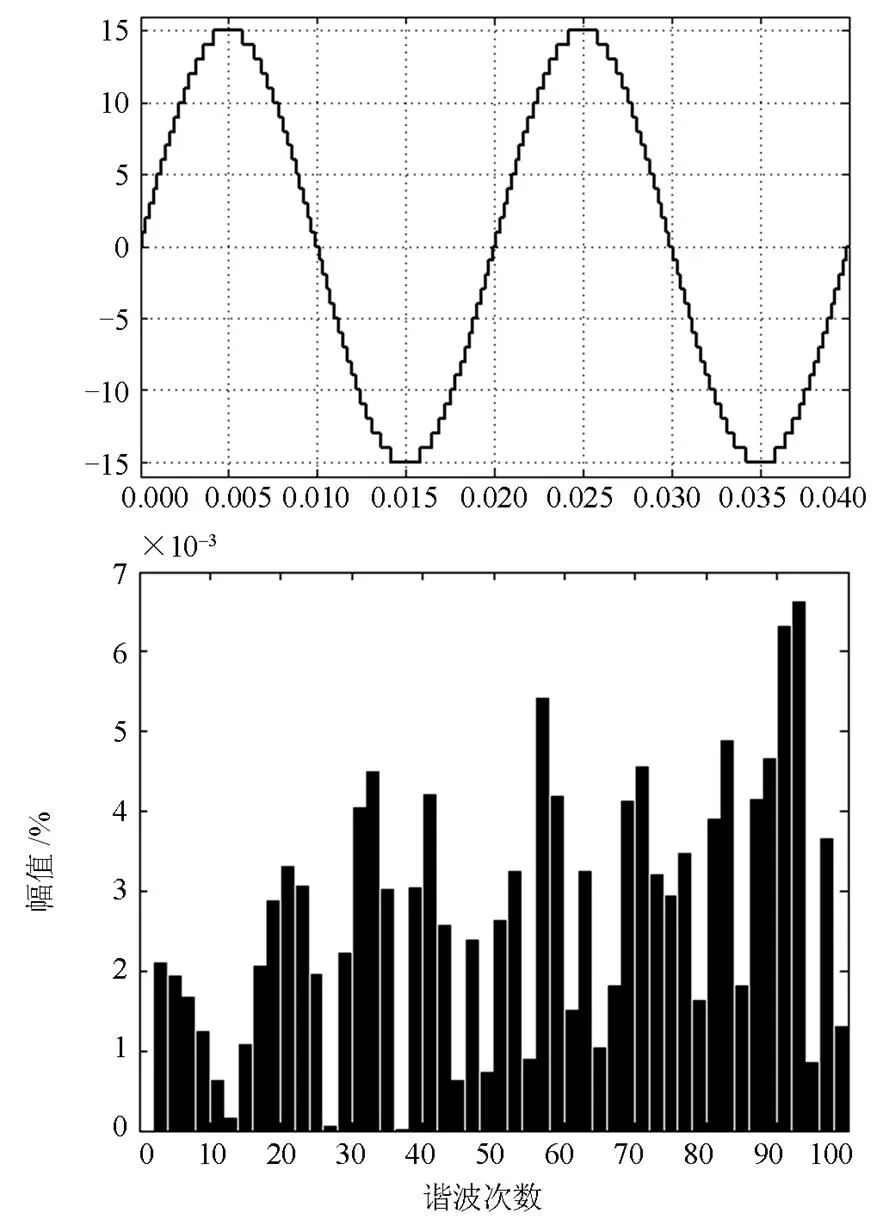
图6当时的输出电压及其各次谐波含量

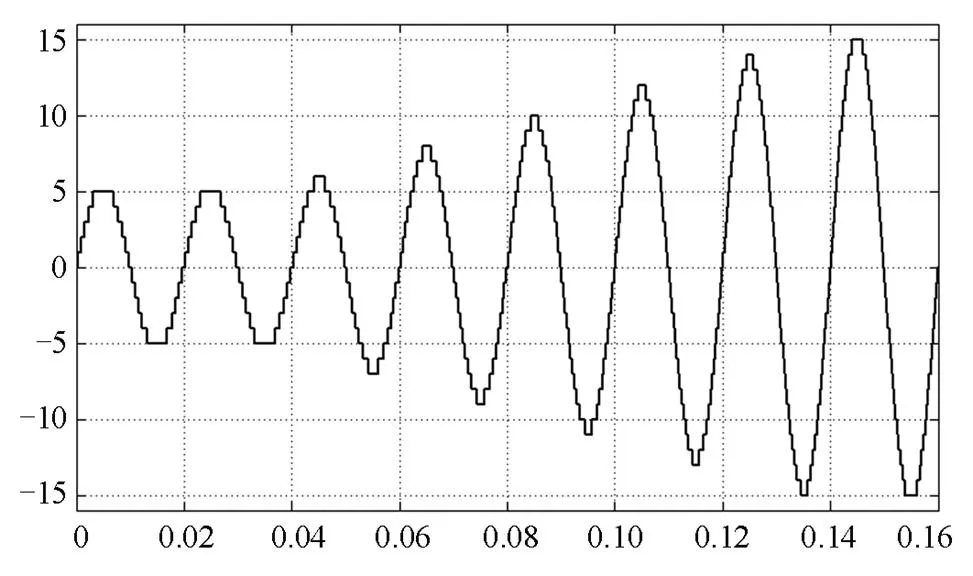
图7级联逆变器的输出电压

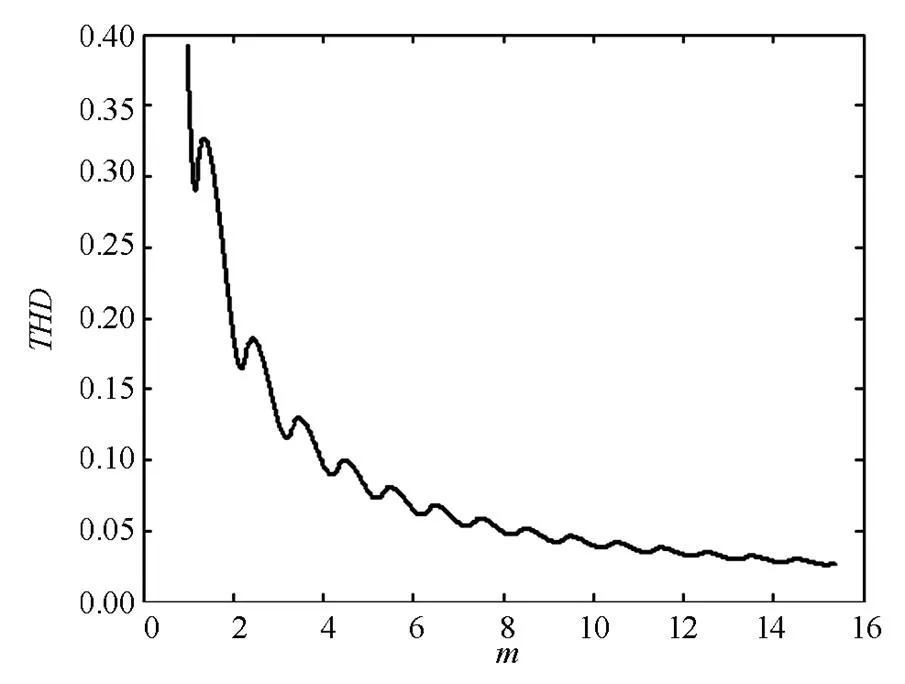
图8总谐波失真随调制系数变化曲线

5 结论

阶梯调制是级联型逆变器的一种重要的调制策略。本文经过严格的数学推导，提出了一种最小化总谐波失真的阶梯调制在线算法，总谐波失真总体趋势随调制系数的增大而减小，当调制系数为7.96和13.06时，总谐波失真分别达到5%和3%。

为了克服牛顿—拉普逊迭代法在求取导通角时计算复杂度高的缺点，本文提出了一种幂函数近似求取调制参数的方法，该方法大大简化了计算量。仿真结果证实了这些方法的有效性。

[1] 张民, 贺仁睦, 孙哲, 等. 基于PSCAD/EMTDC的直流控制保护仿真系统仿真平台及其在直流工程中的应用[J]. 电力系统保护与控制, 2013, 41(3): 112-117.

ZHANG Min, HE Ren-mu, SUN Zhe, et al. The HVDC control and protection simulation platform based on PSCAD/EMTDC and its application in HVDC projects[J]. Power System Protection and Control, 2013, 41(3): 112- 117.

[2] ESFANDIARI E, MARIUN N, MARHABAN M H, et al. Switch-ladder: reliable and efficient multilevel inverter[J]. Electronics Letters, 2010, 46(9): 646-647.

[3] ESFANDIARI E, MARIUN N B. Experimental results of 47-level switch-ladder multilevel inverter[J]. IEEE Trans on Industrial Electronics, 2013, 60(11): 4960-4967.

[4] LIANG Y, NWANKPA C O. A new type of STATCOM based on cascading voltage-source inverters with phase-shifted unipolar SPWM[J]. IEEE Trans on Industry Applications, 1999, 35(5): 1118-1123.

[5] 费万民, 都小利, 居荣, 等. 基于等面积法的多电平逆变器SPWM方法[J]. 电工技术学报, 2010, 25(3): 89-96.

FEI Wan-min, DU Xiao-li, JU Rong, et al. A novel PWM method for multilevel inverters[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 89-96.

[6] 陆志国, 赵丽丽, 吴春军, 等. 一种新型的三相桥级联型PWM变换器[J]. 电力系统保护与控制, 2012, 40(24): 131-137.

LU Zhi-guo, ZHAO Li-li, WU Chun-jun, et al. A novel three-phase-bridge cascaded PWM converter[J]. Power System Protection and Control, 2012, 40(24): 131-137.

[7] 费万民, 吕征宇, 姚文熙. 多电平逆变器特定谐波消除脉宽调制方法的仿真研究[J]. 中国电机工程学报, 2004, 24(1): 102-106.

FEI Wan-min, Lü Zheng-yu, YAO Wen-xi. Research of selected harmonic elimination PWM technique applicable to multi-level voltage inverters[J]. Proceedings of the CSEE, 2004, 24(1): 102-106.

[8] 费万民, 阮新波, 张艳丽, 等. 多电平逆变器特定谐波消除脉宽调制方法的初值问题研究[J]. 中国电机工程学报, 2007, 27(13): 87-92.

FEI Wan-min, RUAN Xin-bo, ZHANG Yan-li, et al. Research on the initial values of SHEPWM method for multi-level voltage inverters[J]. Proceedings of the CSEE, 2007, 27(13): 87-92.

[9] 许爱国, 谢少军. 阶梯波合成逆变器的波形调制技术研究[J]. 中国电机工程学报, 2009, 29(21): 34-39.

XU Ai-guo, XIE Shao-jun. Research on waveform modulatioin technique for staircase inverters[J]. Proceedings of the CSEE, 2009, 29(21): 34-39.

[10] 姚志垒, 肖岚. 基于改进DPC-SVM的三相并网逆变器[J]. 电力系统保护与控制, 2013, 41(4): 141-147.

YAO Zhi-lei, XIAO Lan. Three-phase grid-connected inverters with improved DPC-SVM[J]. Power System Protection and Control, 2013, 41(4): 141-147.

[11] 常伟, 史丽萍, 王思捷, 等. 空间矢量调制技术在6 kV级联静止同步补偿器中的应用[J]. 电力系统保护与控制, 2012, 40(12): 95-99, 140.

CHANG Wei, SHI Li-ping, WANG Si-jie, et al. Application of space vector modulation in 6kV cascade STATCOM[J]. Power System Protection and Control, 2012, 40(12): 95-99, 140.

[12] 王兆宇, 艾芊. 三电平逆变器空间矢量调制及中点电压控制[J]. 电力系统保护与控制, 2011, 39(20): 131-136.

WANG Zhao-yu, AI Qian. Space vector modulation for three-level inverter and neutral point potential control[J]. Power System Protection and Control, 2011, 39(20): 131-136.

[13] 倪喜军, 赵剑锋, 曹武, 等. 开关损耗优化的级联型逆变器全区域空间矢量调制策略[J]. 电工技术学报, 2012, 27(4): 101-109.

NI Xi-jun, ZHAO Jian-feng, CAO Wu, et al. Switching loss optimized SVPWM algorithm for cascade multilevel inverters in all region[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 101-109.

[14] 王翠. n级逆变器SVPWM调制零序电压优化算法[J]. 电工技术学报, 2013, 28(6): 158-164.

WANG Cui. An optimal algorithm on zero order voltage of space vector PWM modulation for n-cell inverters[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 158-164.

[15] 周明磊, 游小杰, 王琛琛, 等. 特定次谐波消除调制方式的谐波特性分析[J]. 电工技术学报, 2013, 28(9): 11-20.

ZHOU Ming-lei, YOU Xiao-jie, WANG Chen-chen, et al. Harmonic analysis of selected harmonic elimination pulse width modulation[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 11-20.

[16] TOLBERT L M, PENG F Z, HABETLER T G. Multilevel converters for large electric drives[J]. IEEE Trans on Industry Applications,1999,35(1): 36-44.

[17] SIRISUKPRASERT S, LAI J, LIU T. Optimum harmonic reduction with a wide range of modulation indexes for multilevel converters[J]. IEEE Trans on Industrial Electronics, 2002, 49(4): 875-881.

[18] FILHO F, TOLBERT L M, YUE C, et al. Real-time selective harmonic minimization for multilevel inverters connected to solar panels using artificial neural network angle generation[J]. IEEE Trans on Industry Applications, 2011, 47(5): 2117-2124.

[19] JIN W, AHAMADI D. A precise and practical harmonic elimination method for multilevel inverters[J]. IEEE Trans on Industry Applications, 2010, 46(2): 857-865.

[20] OZPINECI B, TOLBERT L M, CHIASSON J N. Harmonic optimization of multilevel converters using genetic algorithm[J]. IEEE Power Electron Lett, 2005, 3(3): 92-95.

[21] CHIASSON J N, TOLBERT L M, MCKENZIE K J, et al. A unified approach to solving the harmonic elimination equations in multilevel converters[J]. IEEE Trans on Power Electronics, 2004, 19(2): 478-490.

[22] KANG DW, KIM HC, KIM TJ, et al. A simple method for acquiring the conducting angle in a multilevel cascaded inverter using step pulse waves[J]. IEE ProcElectric Power Applications, 2005, 152(1): 103-111.

[23] 陈元娣, 夏敏学, 朱忠尼. 基于阶梯波与瞬时值反馈混合控制的光伏并网级联逆变器[J]. 电力系统自动化, 2012, 36(14): 172-176, 185.

CHEN Yuan-di, XIA Min-xue, ZHU Zhong-ni. Photovoltaic grid-connected cascaded inverter based on stepped waveforms and instantaneous value feedback hybrid control[J]. Automation of Electric Power Systems, 2012, 36(14): 172-176, 185.

[24] 陈元娣, 刘涤尘, 宋庆国, 等. 阶梯波调制级联逆变器触发角的一种简便算法[J]. 电工电能新技术, 2010, 29(1): 35-40.

CHEN Yuan-di, LIU Di-chen, SONG Qing-guo, et al. A simple algorithm of trigger angle for step wave modulated cascade inverters[J]. Advanced Technology of Electrical Engineering and Energy, 2010, 29(1): 35-40.

[25] HUANG F. Near optimal approach in the design and implementation of multilevel voltage source inverters[J]. IEE Proceedings Electric Power Applications, 1999, 146(6): 661-666.

[26] DIONG B, SEPAHVAND H, CORZINE K A. Harmonic distortion optimization of cascaded H-bridge inverters considering device voltage drops and noninteger DC voltage ratios[J]. IEEE Trans on Industrial Electronics, 2013, 60(8): 3106-3114.

[27] HAGH M T, TAGHIZADEH H, RAZI K. Harmonic minimization in multilevel inverters using modified species-based particle swarm optimization[J]. IEEE Trans on Power Electronics, 2009, 24(10): 2259-2267.

[28] LIU Y, HONG H, HUANG A Q. Real-time calculation of switching angles minimizing THD for multilevel inverters with step modulation[J]. IEEE Trans on Industrial Electronics, 2009, 56(2): 285-293.

[29] LIU Y, HONG H, HUANG A Q. Real-time algorithm for minimizing THD in multilevel inverters with unequal or varying voltage steps under staircase modulation[J]. IEEE Trans on Industrial Electronics, 2009, 56(6): 2249-2258.

Staircase modulation strategy with minimum total harmonic distortion for cascaded multilevel inverters

LI Su-fei, LI Guo-jie, ZHAI Deng-hui, WANG Wei-xing

(1. Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education (Department of Electrical Engineering, Shanghai Jiao Tong University), Shanghai 200240, China; 2. XJ Electric Co., Ltd., Xuchang 461000, China)

In order to decrease the output-voltage harmonic components of cascaded multilevel inverter, this paper proposes a novel staircase modulation strategy based on Karush-Kuhn-Tucker (KKT) conditions. With KKT conditions and rigorous mathematical derivation, this paper acquires the corresponding calculation method of conducting angles, and the proposed staircase modulation strategy can minimize the total harmonic distortion (THD) under arbitrary modulation index. Furthermore, this paper takes advantage of Newton-Raphson iteration method to obtain the key parameter in the aforementioned conducting angle calculation method. To overcome the deficiency of slow calculation speed of Newton-Raphson iteration method, this paper proposes the power function approximation approach to simplify calculation complexity. Finally, this paper undertakes simulation analysis and obtains the output voltage waveforms and their frequency-domain distributions under both fixed and varying modulation indices. Simulation results verify the effectiveness of the modulation strategy. This work is supported by National Natural Science Foundation of China (No. 51477098), National High Technology Research and Development Program of China (863 Program) (No. 2012AA050212), and International S&T Cooperation Program of China (No. 2013DFG71630).

cascaded multilevel inverter; THD; staircase modulation; KKT conditions; function approximation

TM464

A

1674-3415(2014)19-0008-10

2013-12-23；

2014-04-09

李素非(1988-)，男，硕士，研究方向为局部放电在线监测、电力电子技术等；E-mail: lsf5072@126.com

李国杰(1965-)，男，通信作者，博士，教授，主要研究方向为新能源控制与接入、微电网分析与控制。E-mail: liguojie@sjtu.edu.cn

翟登辉(1984-)，男，硕士，工程师，研究方向为微电网系统及电力电子设备研发。

国家自然科学基金(51477098)；国家高技术研究发展计划863计划(2012AA050212)；国家国际科技合作专项项目(2013DFG71630)