深基坑三维应力场和渗流场耦合分析与模拟

(广东水利电力职业技术学院，广州 510635)

1 研究背景

随着大规模城市地下空间的开发与利用，深基坑工程日益增多，且规模和深度也在逐渐加大。在一些地下水位较高的城市，基坑开挖过程中地下水是经常遇到的问题。地下水渗流影响土体的应力状态，而应力状态的改变又使孔隙介质中渗流空间发生改变，进而改变地下水流动的水力特征。在深基坑工程中，由于基坑及其周边地区的地下水位存在较大的水头差，使得基坑附近存在明显的地下水渗流现象，进而影响到深基坑的稳定性，并势必影响周边建筑物的安全和稳定。因此，在高水位地区的深基坑开挖，基坑周围渗流所引起的环境日益突出[1]。

深基坑降水施工过程实质上是渗流场和应力场相互影响、相互作用的过程。目前，关于基坑降水提出了许多分析计算模型，主要有水土分算模型、部分耦合模型[2-3],以及基于比奥固结理论的全耦合模型[4-5]。深基坑开挖过程中，地下水的渗流是一个非稳态非线性渗流过程。在基坑开挖过程中，基坑应力场作用在基坑周围土体上，使得土的孔隙比、渗透系数等渗透特性发生了改变；与此同时，开挖范围的扩大、基坑的分级降水、基坑周围土体渗流场的改变都会影响土体的应力状态，进而改变土体的变形计算参数。因此，在进行基坑分析计算时不仅应考虑变形参数E随应力状态的变化，而且还要考虑渗透系数随有效应力状态的变化。

目前国内外对基坑降水引起的渗流和变形采用的计算模型大都采用线弹性假设，而且没有考虑到土体渗透性随应力场的变化而变化，与实际基坑工作性状存在较大的差别。因此，在基坑分析计算中，考虑渗流场和应力场的耦合情况，不但可以使计算结果更加接近实际，而且可以为基坑降水和支护优化设计提供理论依据。本文采用完全耦合模型，考虑渗流参数与变形计算参数的耦合变化，针对三维典型深基坑，预测基坑在降水开挖过程中产生的变形。

2 非饱和渗流-应力全耦合模型

Bishop提出的适用于非饱和土的有效应力原理[6]：

σ′=σ-χuw。

(1)

式中：σ′为土中的有效应力；σ为土中总应力；uw为土体中的孔隙水压力；χ为面积系数，与土体的饱和度sr有关。

假定土骨架变形为线弹性和微小变形，地下水渗流符合达西定律，且不可压缩或微压缩，则各向同性非饱和土体的三维比奥固结方程如下：

(2)

式中：G为剪切模量；ν为泊松比；wx，wy，wz分别为x，y和z方向上的位移分量；u为孔隙水压力；n为孔隙率；γw为水的重度；γd为土的干重度。

饱和-非饱和土进出水量速率之差等于单元体内水量增减速率，得到非饱和土渗流连续性方程如下[7]：

(3)

式中：kx，ky，kz分别为x，y和z方向上的渗透系数；θ为体积含水量,θ=nsr；Ss为单位土体的贮水率。

上述位移平衡微分方程和水流连续性方程采用Galerkin加权余量法离散方程，得到增量形式表达的有限元方程：

(4)

3 邓肯-张非线性模型

采用非线性弹性的邓肯-张模型，考虑到弹性常数E-μ随着土体应力状态的变化而变化，根据广义虎克定律建立增量型本构关系：

{Δσ}=D{Δε} 。

(5)

式中：D为刚度矩阵，地基中任一点的切线模量和切线泊松比分别为:

(6)

(7)

式中：c和φ为强度指标；k，n，Rf，G，F，D为试验参数，可以由常规三轴试验确定；σ1，σ3分别为大主应力和小主应力；Pa为标准大气压。

4 渗透系数的非线性耦合响应

土体中地下水位变化而产生的固结过程，实质上就是渗流场与应力场的耦合作用过程。渗流产生的动、静水压力改变土体的应力状态，应力状态的改变又将导致土体渗透性质的变化。非饱和多孔介质土体的渗透性与其饱和度和孔隙率相关，假定上述两者的影响彼此独立，土体渗透系数的表达式如下：

(8)

式中：ks为饱和度影响系数；kn为孔隙率的影响系数；k0为土体初始渗透系数。

Nguyen和Durso[8]在1983年通过试验证明ks与饱和度之间满足如下关系：

(9)

李培超等[9]认为土体孔隙率影响系数kn与土体的初始孔隙率、体积变形相关

(10)

式中：n0为初始孔隙率；εV为体应变。

5 基坑开挖过程中的荷载

基坑降水开挖过程中的荷载主要表现为地下水位降低所引起的附加荷载，基坑开挖过程中引起的开挖荷载。

5.1 降水荷载

降低基坑内地下水位引起的荷载为

Pw=βΔhγw,

(11)

式中：Pw为水位变化施加于地层的荷载；β为折减系数，通常砂土层取1，黏性土层取0.5；Δh为Δt时间内含水层的水位变化幅度。

5.2 开挖荷载

开挖荷载是在开挖边界上的卸载点的荷载：

(12)

式中：M为被挖掉的单元数；σ0为初始应力场；B为应变位移矩阵；N为形函数。

6 工程应用实例

6.1 工程概况

某地处闹市区的工程基坑，平面尺寸65 m×40 m，设2层地下室，基坑设计开挖深度为9.25～9.75 m，局部电梯井深度达13.15 m，采用0.8 m厚的地下连续墙作为基坑支护结构兼防渗帷幕，同时兼作为地下室外墙。

基坑所在区域内地下水主要以潜水为主，地下水位较高，一般在地表以下2.5 m左右，由于基坑开挖面积较大，在基坑内设置2道钢筋混凝土支撑，支撑设置高程分别为-2.50，-6.50 m。采用对撑(1 000 mm×800 mm)和角撑(800 mm×600 mm)相结合的支撑方式。

基坑降水采用坑内深井降水，在坑内设置6个降水井，降水井深度为18.5 m。为了防止一次性降水对周边环境的影响，采取根据开挖进程分级降水的方式。基坑逐级进行开挖，降水后坑内的地下水位一般低于开挖面以下0.5～2.0 m。基坑的平面尺寸及降水井布置如图1所示。

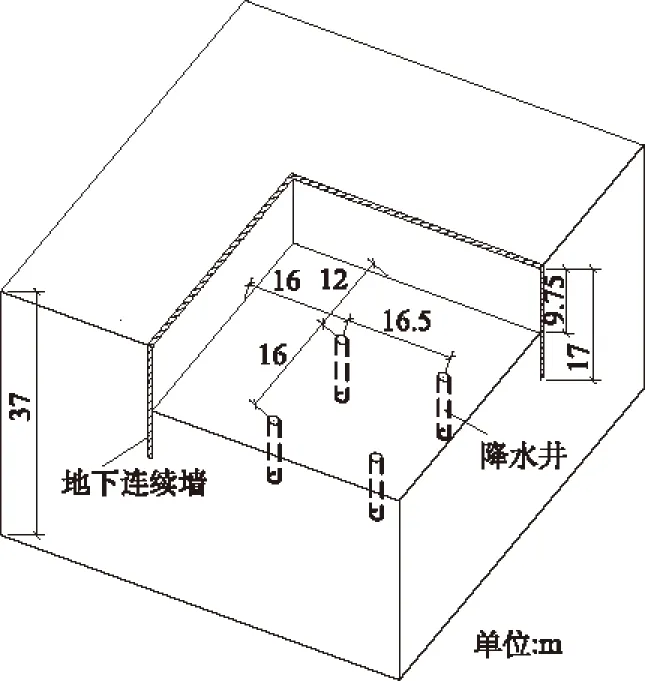
图1 计算模型示意图

表2基坑土层计算参数

Table2Parametersofsoillayersofthefoundationpitforcalculation

土层厚度/mγ/(kN·m-3)e0ø′/(°) c′/kPaK0/(cm·s-1)RfknGFDkur杂填土、素填土1.5018.1—24.07.4—0.782000.550.2801300砂质粉土10.0018.90.7833.47.21.450.805000.550.2801480粉砂夹粉土4.4019.10.7239.07.23.670.805500.550.2801520粉砂3.4019.30.6339.87.01.880.807000.600.3001680粉质黏土21.2018.30.9430.018.70.250.752500.500.26011 000

6.2 施工过程

基坑降水和开挖均采用分级进行，做到“边降水、边开挖”，避免一次性降水过低，引起渗透压力过大，与此同时没有及时设置支撑，而引起地面产生过大的沉降。施工过程顺序如表1所示。

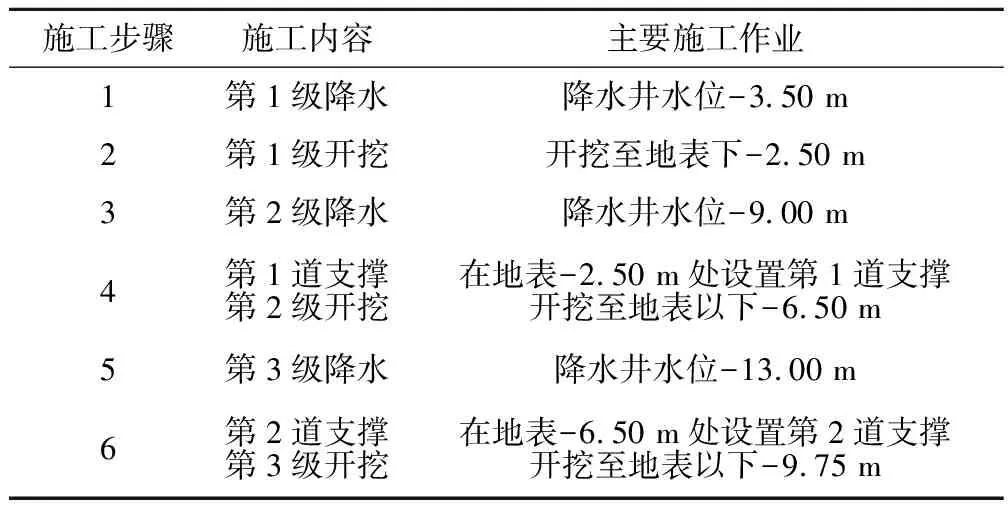
表1 基坑施工顺序

6.3 模型参数

计算范围内土层共5层，耦合分析模型涉及参数包含：内摩擦角，黏聚力，土体模量有关参数(k，n)，泊松比有关参数，渗透系数有关参数等。模型计算参数如表2所示。

地下连续墙采用钢筋混凝土结构，连续墙体的计算参数如表3所示。

表3 地下连续墙体材料参数

6.4 结果分析

根据上述数学模型，对某基坑工程进行有限元耦合模型分析，得出基坑围护结构及基坑外侧土体的变形场分布。图2、图3分别为地下连续墙短边和长边中点处沿深度方向的侧向位移曲线。图4、图5分别为基坑外侧长边方向和短边方向地面沉降曲线。图6为1/4基坑外侧在不同施工阶段的地面沉降(U3为竖直方向沉降)云图。

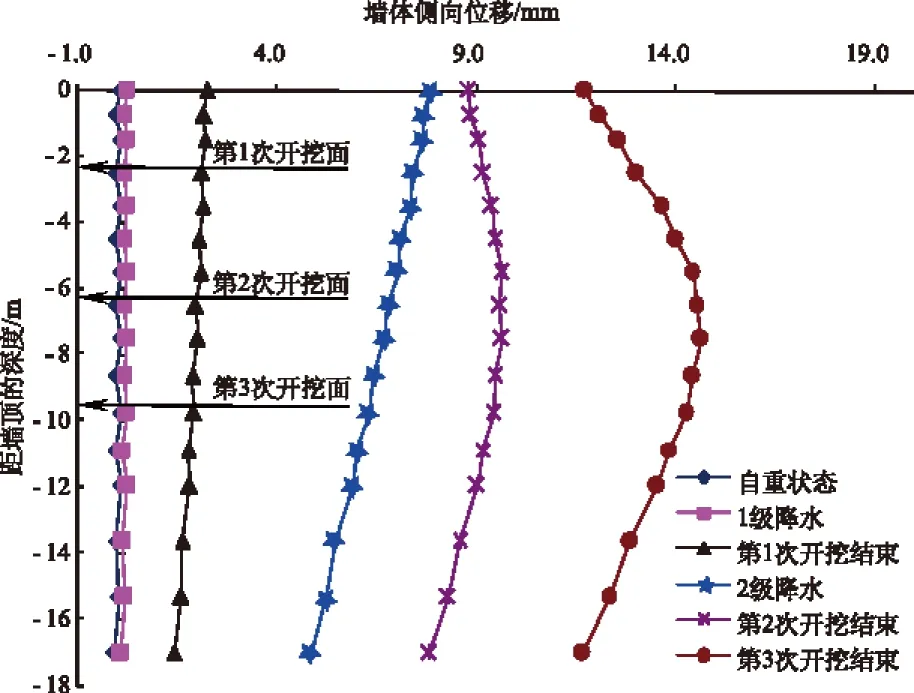
图2 地下连续墙短边中点的侧向位移

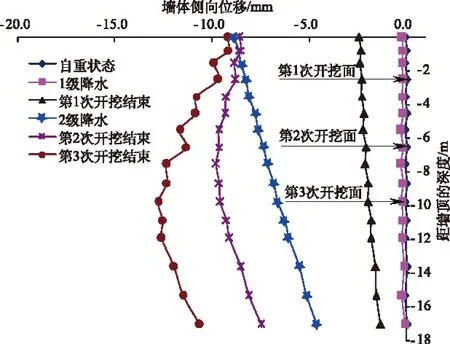
图3 地下连续墙长边中点的侧向位移

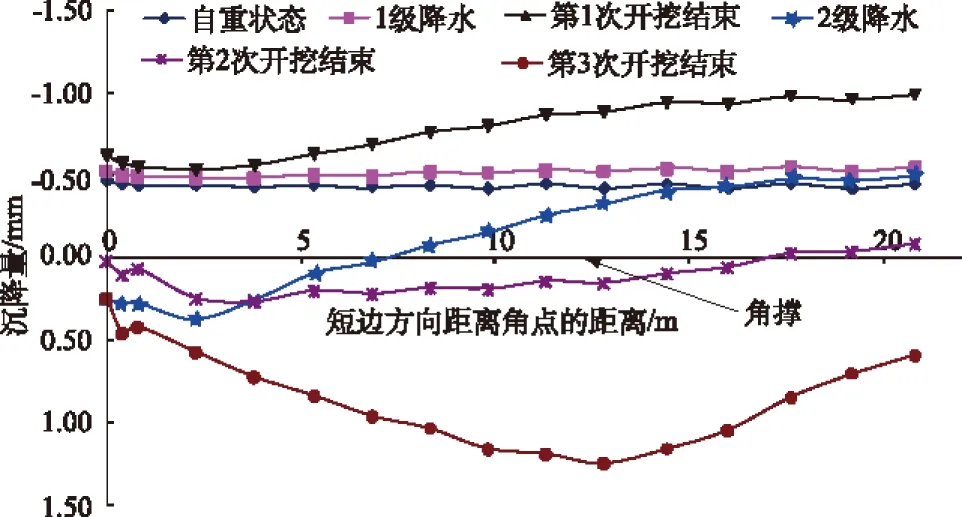
图4 基坑周围沿短边方向地面沉降

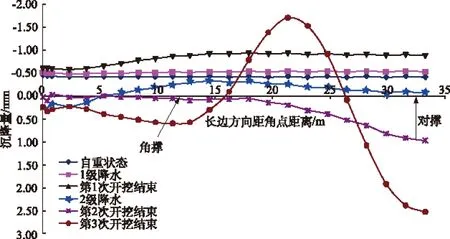
图5 基坑周围沿长边方向地面沉降

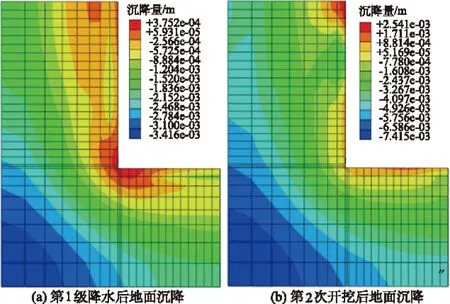
图6 基坑周围地面沉降图

由基坑周围地下连续墙的侧向位移图可知，在基坑开挖结束后，最大侧向位移基本上发生在基坑开挖面附近，短边方向侧向位移最大值14.6 mm，长边方向侧向位移最大值12.7 mm。侧向位移沿深度方向的分布图可以看出：设置支撑有效地限制了基坑顶部的侧向位移，侧向位移随着开挖深度的加大，逐步有向基坑底面转移的趋势。在基坑开挖过程中，未设支撑之前，长短边侧向位移均表现为顶部大、底部小接近于直线的趋势；当设置支撑后，上部的侧向位移逐步得到有效限制，侧向逐渐向基坑下部传递，均表现为开挖面附近侧向位移最大。这说明合理的支撑结构明显改变了支护结构侧向位移的变化趋势，有效地保护了基坑围护结构的变形。

6.5 监测结果对比

对此深基坑工程开挖进行变形监测，监测数据表明，开挖施工结束后，在基坑长边方向，顶部侧向位移为10.8 mm；在短边方向上，侧向位移为13.5 mm。通过上述耦合计算，如图2、图3所示，在基坑顶部的长边和短边中点位置侧向位移分别为9.2，11.7 mm。监测数据表明基坑围护结构在长边和短边方向的中点位置最大水平位移分别为13.9 mm和16.0 mm，与本次分析计算的12.7 mm和14.6 mm比较吻合。

根据本基坑开挖过程中，周围地面沉降的监测数据可知，基坑周围地面沉降量监测最大值为5.1 mm，与本工程有限元计算的最大沉降量4.43 mm比较吻合。此外，在基坑围护结构的边缘，沉降量均低于3 mm，这主要是由于合理的设置对应的支撑结构，限制了结构的变形所导致的。此外，周围地面沉降变形最大值并不是发生在紧贴基坑周边，而是发生在距离边缘一定距离的部位。

7 结 论

通过以上三维基坑开挖的有限元分析，可以得到以下主要结论：

(1) 考虑渗流和应力耦合情况下计算基坑变形明显大于传统的不考虑渗流和应力耦合情况下计算的基坑变形，与实际情况相比较发现，耦合计算的成果与实际监测数据更加接近，说明在实际基坑计算分析过程中，采用耦合计算结果更接近实际监测结果。

(2) 基坑在开挖过程中，为了防止在基坑顶部发生较大的侧向位移而导致基坑出现工程事故，应在开挖过程中尽快设置相应的支撑结构，以增加整体结构的刚度，限制顶部的侧向变形。

(3) 基坑周围沉降最大值发生在距离基坑周边一定距离范围内，距离根据基坑开挖深度和支护结构的情况不同而有所差别。但总体上来看，基本上最大沉降发生在基坑周边，当超过该范围后，基坑周围的沉降迅速减小。因此，在基坑施工过程中，周围沉降影响范围内的区域要加强监测工作。

参考文献：

[1] DESAI C S. Seepage Analysis of Earth Banks under Drawdown[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98SM(11): 1143-1163.

[2] 冉启全，顾小云.考虑流变特性的流固耦合地面沉降计算模型[J].中国地质灾害与防治学报，1998,9(2)：99-103.(RAN Qi-quan, GU Xiao-yun. A Coupled Model for Land Subsidence Computation with Consideration of Rheological Property[J]. The Chinese Journal of Geological Hazard and Control，1998，9(2)：99-103. (in Chinese))

[3] 周志芳，朱宏高，陈 静，等.深基坑降水与沉降的非线性耦合计算[J].岩土力学，2004,25(12)：1984-1988. (ZHOU Zhi-fang，ZHU Hong-gao，CHEN Jing，etal. Nonlinear Coupling Calculation between Dewatering and Settlement of Deep Foundation Pits[J]. Rock and Soil Mechanics，2004，25(12):1984-1988.(in Chinese))

[4] GU Xiao-yun, RAN Qi-quan. A 3-D Coupled Model with Consolidation of Rheological Properties[C]∥Proceeding of the Sixth International Symposium on Land Subsidence. Ravenna, Italy, September 25-29, 2000: 355-365.

[5] 吴宏伟，施 群.深基坑开挖中的应力路径[J].土木工程学报，1999,32(6)：53-58.(NG W W C, SHI Qun. Changes of Stress Path Caused by Stress Relief during Excavations[J]. China Civil Engineering Journal, 1999, 32(6): 53-58. (in Chinese))

[6] FREDLUND D G, RAHARDJO H. 非饱和土力学[M]．陈仲颐，张在明，陈愈炯,译．北京：中国建筑工业出版社，1997. (FREDLUND D G, RAHARDJO H. Soil Mechanics for Unsaturated Soils[M]. Translated by CHEN Zhong-yi, ZHANG Zai-ming, CHEN Yu-jiong,etal. Beijing: China Architecture and Building Press, 1997. (in Chinese))

[7] 毛昶熙，段祥宝，李祖贻,等．渗流数值计算与程序应用[M]．南京：河海大学出版社，1999. (MAO Chang-xi, DUAN Xiang-bao, LI Zu-yi,etal. Seepage Numerical Calculation and Program Application[M]. Nanjing: Hohai University, 1999. (in Chinese))

[8] NGUYEN H V, D F DURSO. Absorption of Water by Fiber Webs: An Illustration of Diffusion Transport[J]. TAPPI Journal, 1983, 66(12): 76-79.

[9] 李培超，孔祥言，卢德唐．饱和多孔介质流固耦合渗流的数学模型[J]．水动力学研究与进展(A辑)，2003,18(4)：419-426. (LI Pei-chao, KONG Xiang-yan, LU De-tang. Mathematical Modeling of Flow in Saturated Porous Media on Account of Fluid-Structure Coupling Effect[J]. Journal of Hydrodynamics, 2003, 18(4): 419-426. (in Chinese))