基于区间算术的含分布式电源电网无功优化方法

张勇军，苏杰和，羿应棋



基于区间算术的含分布式电源电网无功优化方法

张勇军，苏杰和，羿应棋

（华南理工大学电力学院，广东 广州 510640）

为了解决分布式电源出力不确定性以及负荷波动性所带来的影响，提出一种基于区间数的含分布式电源电网无功优化方法。介绍区间数和区间算术的概念并建立区间潮流模型；建立含分布式电源电网区间无功优化模型的目标函数和约束条件，并给出采用粒子群算法求解区间无功优化模型的步骤；最后通过Matlab对一个修改后的IEEE14节点系统进行区间无功优化仿真计算，并采用粒子群算法对单一潮流断面进行无功优化验证了所提算法的正确性。仿真结果表明，基于区间算术的无功优化方法能够在计及电网不确定性因素情况下，使得电网趋优运行。

分布式电源；无功优化；区间潮流；粒子群算法

0 引言

系统无功优化是保证系统安全经济运行的重要手段之一。传统的无功优化，是指在系统网络结构和系统负荷给定的情况下，通过调节控制变量，包括发电机电压幅值、电容器组的投切和变压器分接头的调节，使系统在满足各种约束条件下网损达到最小。文献[1-3]从经济性的角度出发给出系统的有功网损最小化作为目标函数，以潮流方程作为等式约束，以及无功补偿量、发电机出力、变压器抽头和电压幅值为不等式约束，通过无功优化不仅可以使全网电压在额定值附近运行，而且还能取得可观的经济效益，使电能质量、系统运行的安全性和经济性完美地结合在一起。

由于可再生能源的分布式电源的出力具有不确定性，这些情况下如果还采用确定性的潮流进行无功优化，就需要将各种可能的情况按不同的组合分别进行分析讨论。显然，若对所有可能出现的情况都做计算既不现实也无必要，计算工作量很大，也不一定能获得满意的结果。

在现有的文献中，计及不确定性因素的无功优化主要用概率分布函数或者模糊隶属度来考虑这些不确定性因素。

文献[5-10]采用概率分布来描述负荷和DG出力的不确定性，并将传统无功优化的潮流计算转化为概率潮流。然而，采用概率分布函数来表示不确定量的前提是概率密度函数能够准确的表示随机量的特征，但实际系统中不论光伏的出力还是负荷都没有精确的表达式能把这种不确定描述出来，所以所计算出来的控制变量不一定能够使电网优化运行。

文献[11]采用模糊集进行无功电压优化控制，但由于模糊控制适用处理不确定的无功优化问题，因此利用模糊集来解决多目标寻优问题。而文献[12-13]则将模糊数引入到潮流计算，由模糊潮流来得到潮流的可能性分布。

然而，在工程中，当一个问题的原始数据不能精确地被知道，而只知其包含在给定的界限范围内，或者原始数据本身就是一个区间而非某个点值时，即可利用区间数学来求解问题的未知解所在的范围或求取区间解。

文献[15]将区间数学引入求解不确定负荷下的潮流问题，以区间量为基础的潮流计算模型出发，采用Kraczyk_Moore区间迭代法进行不确定性负荷潮流计算。同样，文献[16]也采用区间算法进行直流区间潮流计算。但是，这些文献中只是用到区间数来算区间潮流，并没有用来实现无功电压的优化。

因此，本文提出了一种基于区间数的无功优化方法，只需要根据不确定量的区间范围，就可计及所有不确性因素的影响，简单而且容易处理，进而求出电网控制变量，使系统运行于趋优的状态下。

1 相关数学概念

1.1 区间数及区间算术

=[，]={∈R|≤≤} (1)

区间算术的具体运算规则及运算定理请详见于文献[11]。

1.2 区间潮流求解

设系统有个节点，其中，节点1，2，…，为PQ节点，节点(+1)，…，(-1)为PV节点，节点为平衡节点。则潮流方程可写为

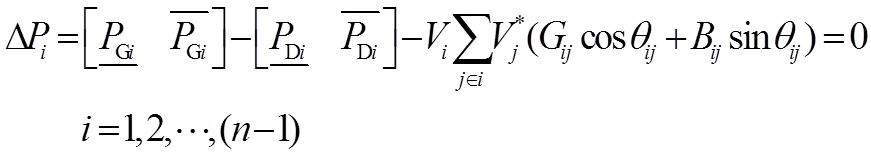
(3)

由计算模型式(2)和式(3)得到的方程组为(+-1)阶方程组，为了方便表述，将其表示为

() = 0 (4)

首先求Krawczyk-Moore算子，给定初始区间为

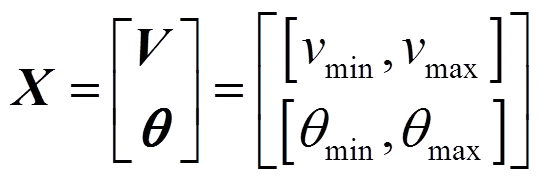
式中：为电压幅值，为维向量；为电压相角，为(-1)维向量；下标max、min分别表示上、下限。取中点mid()作为近似零点*，()在此点的值为(*)。

方程组(4)中，()的雅可比矩阵的具有包含单调性的区间扩展为

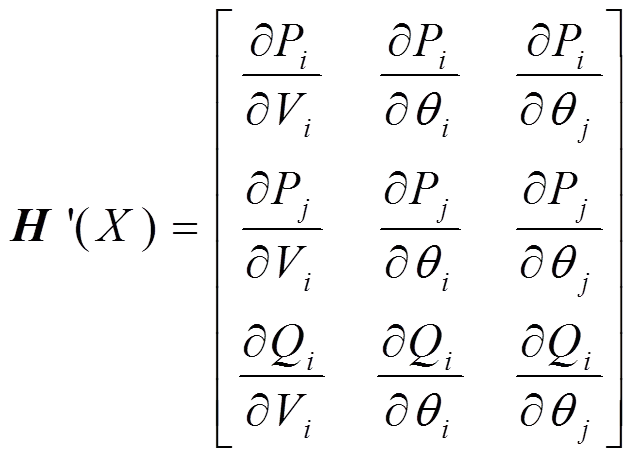
其中：=1，2，…，；=(+1)，(+2)，…，(-1)。

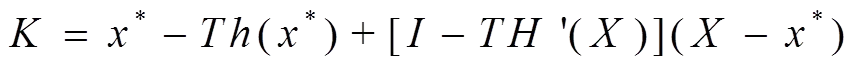
利用K算子进行迭代

(8)

即可得到潮流方程电压和相角的区间解。

2 区间无功优化模型

（1）目标函数

选取目标函数为网损最小，即

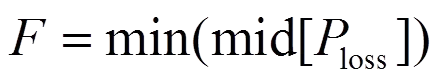
式中，mid[]为系统区间网损的中点值。

（2）潮流方程等式约束

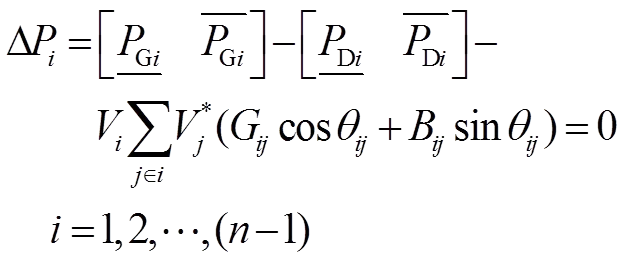
（3）不等式约束

控制变量不等式约束为

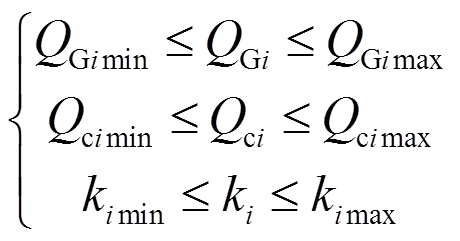
式中：_Gmin和为发电机组的无功出力的上下限；和为无功补偿设备容量的上下限；k和k有载变压器的变比上下限。

状态变量的约束，即节点电压的区间约束为

3 区间无功优化的求解

粒子群算法在搜索空间的位置对应于无功优化的控制变量，包括发电机端电压参与调压、有载变压器变比调压、增加无功补偿设备进行调压。

无功优化问题的状态约束，可通过设定控制变量的搜索边界自动满足，状态变量约束可以采用罚函数法处理。应用罚函数法，可建立适应度函数：

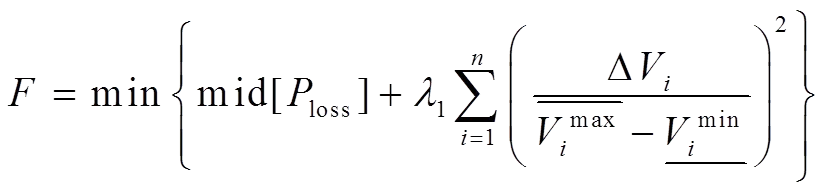
(14)

所以，采用粒子群算法对基于区间数的无功优化算法的求解步骤如下：

步骤1：在三组控制变量的初始化范围内，对由这三组控制变量的粒子群进行随机初始化，包括随机位置和速度，第个粒子的位置表示为

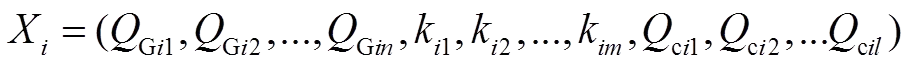
第个粒子的速度表示为

第个粒子经过的历史最好点表示为

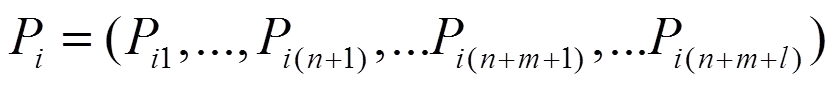
群体内所有粒子所经过的最好的点表示为

步骤2：给出电压和相角的初始区间，计算Krawczyk-Moore算子K如式(7)，利用K算子进行迭代，直到，得到收敛的电压幅值和相角的区间，计算每个粒子的适应值如式(13)。

步骤3：对每个粒子，将其适应值与所经历过的最好位置的适应值进行比较，如果更好，则将其作为粒子的个体历史的最优值，用当前的位置(即发电机机端电压、变压器档位、无功补偿设备容量这三组控制变量的值)更新个体的最好位置。

步骤4：对每个粒子，将其历史最优适应值与群体内或领域内所经的最好位置的适应值进行比较，若更好，则将其作为当前的全局最好位置。

步骤5：根据式(15)和式(16)对粒子的速度的位置和速度进行更新，即

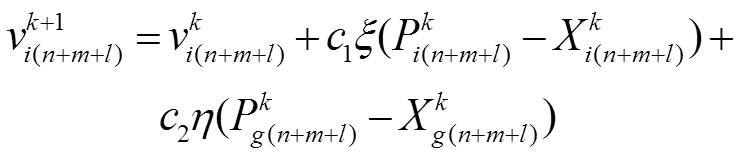
(16)

步骤6：判断是否达到最大迭代次数或者适应度函数的值相邻几代小于，若是则结束计算，否则转向步骤2，直到达到终止条件。

4 算例分析

本文对IEEE14节点系统进行修改，额定容量为49.5 MW的风电场通过10 km 架空线路LGJ-240接到额定容量为50 MVA、型号为SF29升压变压器在节点5并网如图1。算例选取33台额定功率为1.5 MW的变速恒频双馈风电机组，负荷以给定负荷的为区间，发电机以给定出力为区间出力，风电场以[0，49.5] MW作为风电场的区间出力。本文采用Matlab编写区间潮流程序及基于粒子群算法的区间无功优化，得出网损值的迭代曲线如图2所示。表1为IEEE14节点系统优化前后的对比，表2为最优控制方案。

为了具有可比性，但又考虑到无法一一列举各种情况，图3和图4给出了与区间无功优化相对比的两种基于PSO的确定无功优化，它们表示IEEE14节点系统在确定网架、发电机、负荷参数情况下，并入风电场和未并入风电场的确定无功优化情况下网损迭代曲线如图3和图4。表3和表4分别是在确定无功优化之后得到的电压标幺值以及对应的无功优化控制方案。

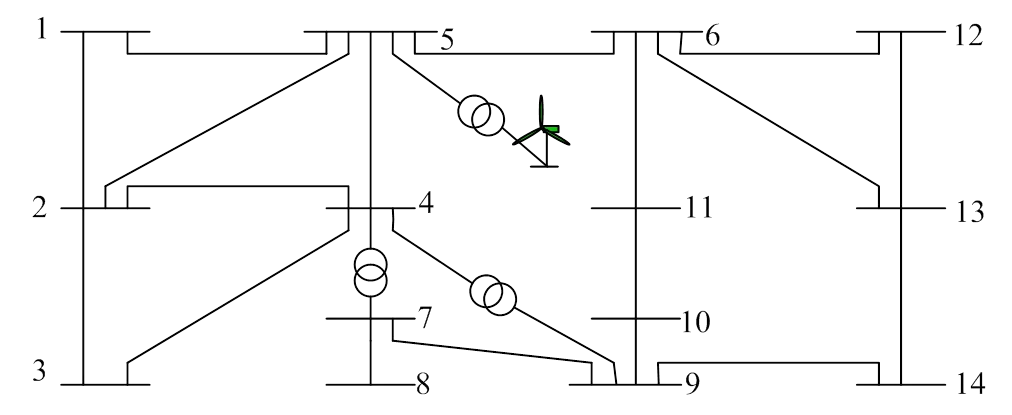
图1修改的IEEE14节点系统

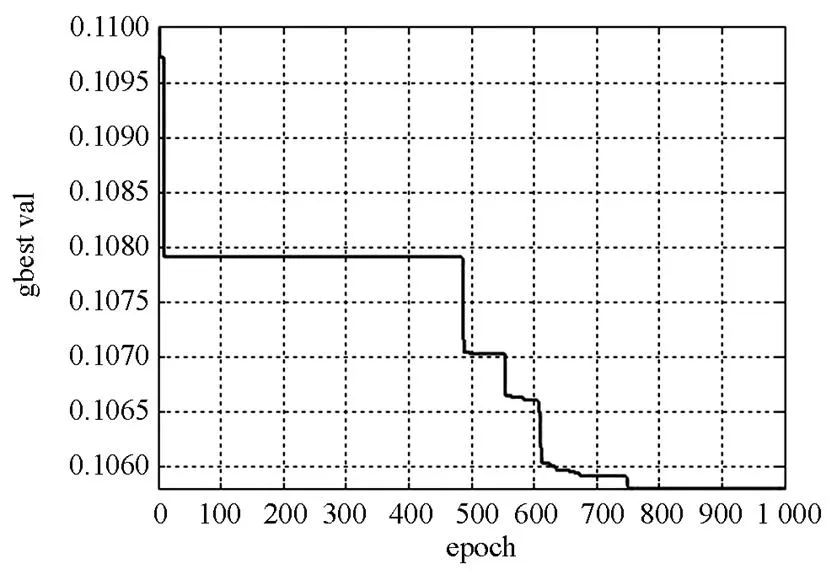
图2 区间无功优化网损中点值迭代曲线

Fig. 2Mid-range of power loss iteration curve based on interval reactive power optimization

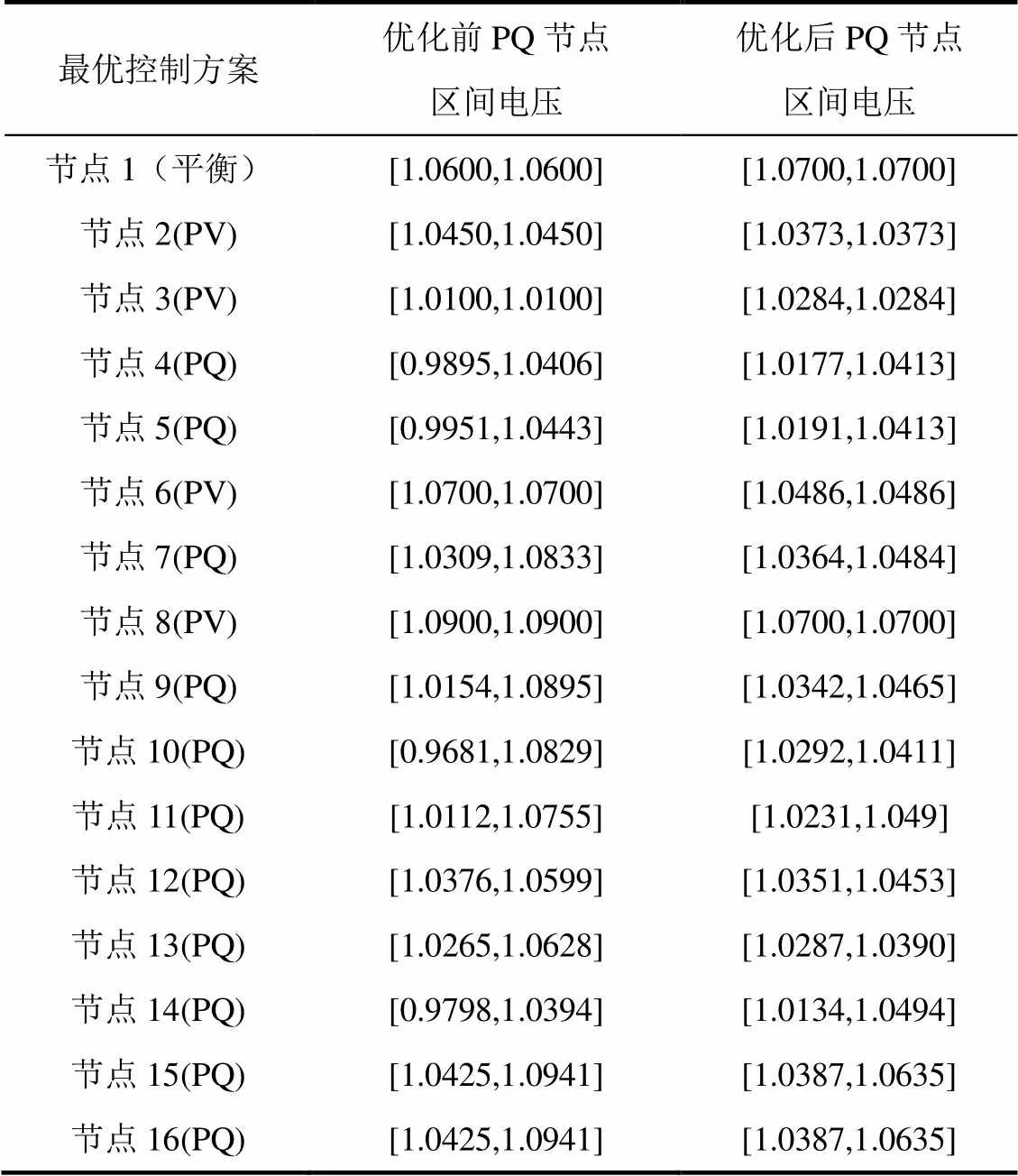
表1 优化前后节点区间电压

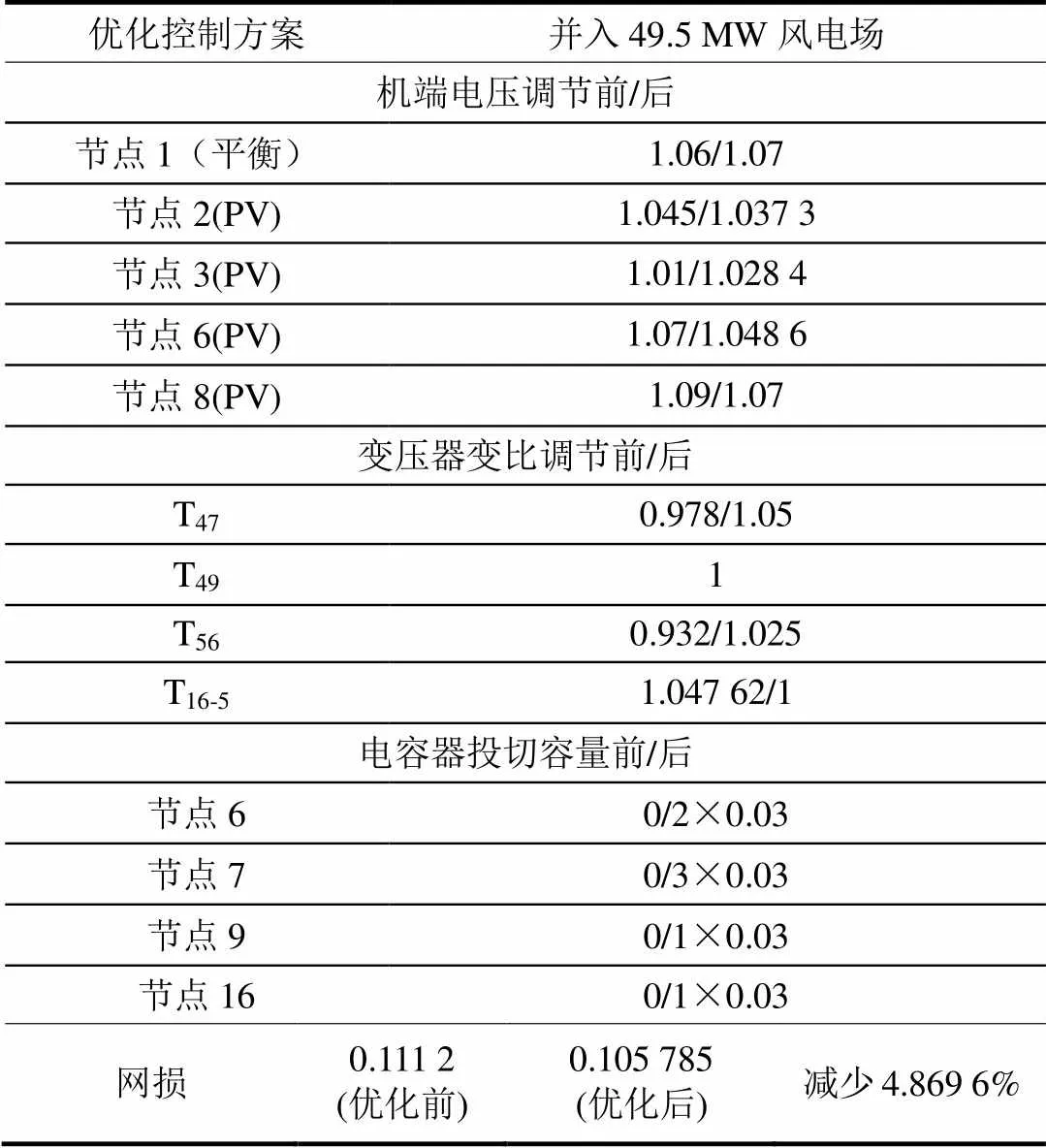
表2 区间无功优化的控制方案

由图和表1和表2可知，在计及发电机被迫停运、负荷波动及风电场出力不确定性时，进行无功优化前，由区间潮流计算得到的区间电压跨度相对较大，而且节点的区间电压也会越过区间安全电压[0.97,1.07]；进行无功优化后，而且都能把节点区间电压约束在安全的电压区间之内。

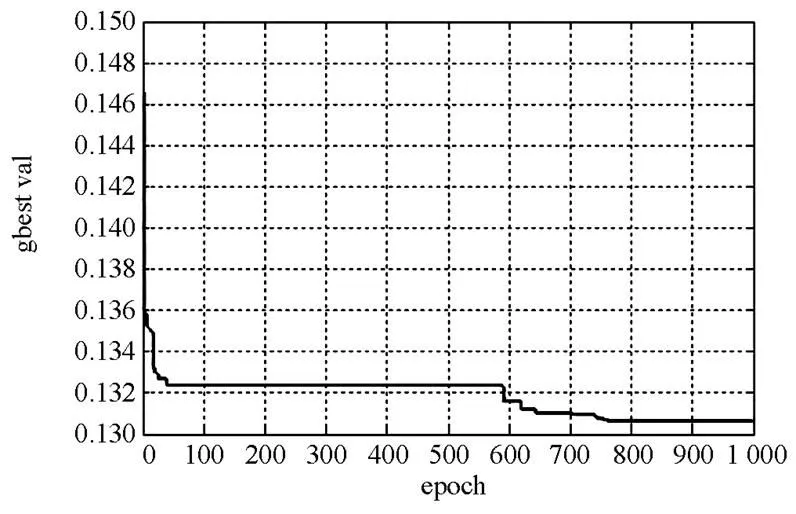
图3 未并入风电场时网损迭代曲线

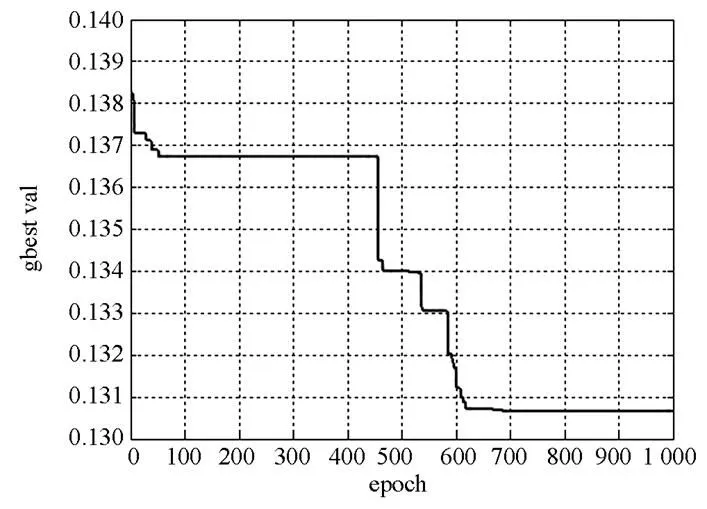
图4 并入49.5 MW风电场时网损迭代曲线

表3并入/未并入风电场时优化电压标幺值

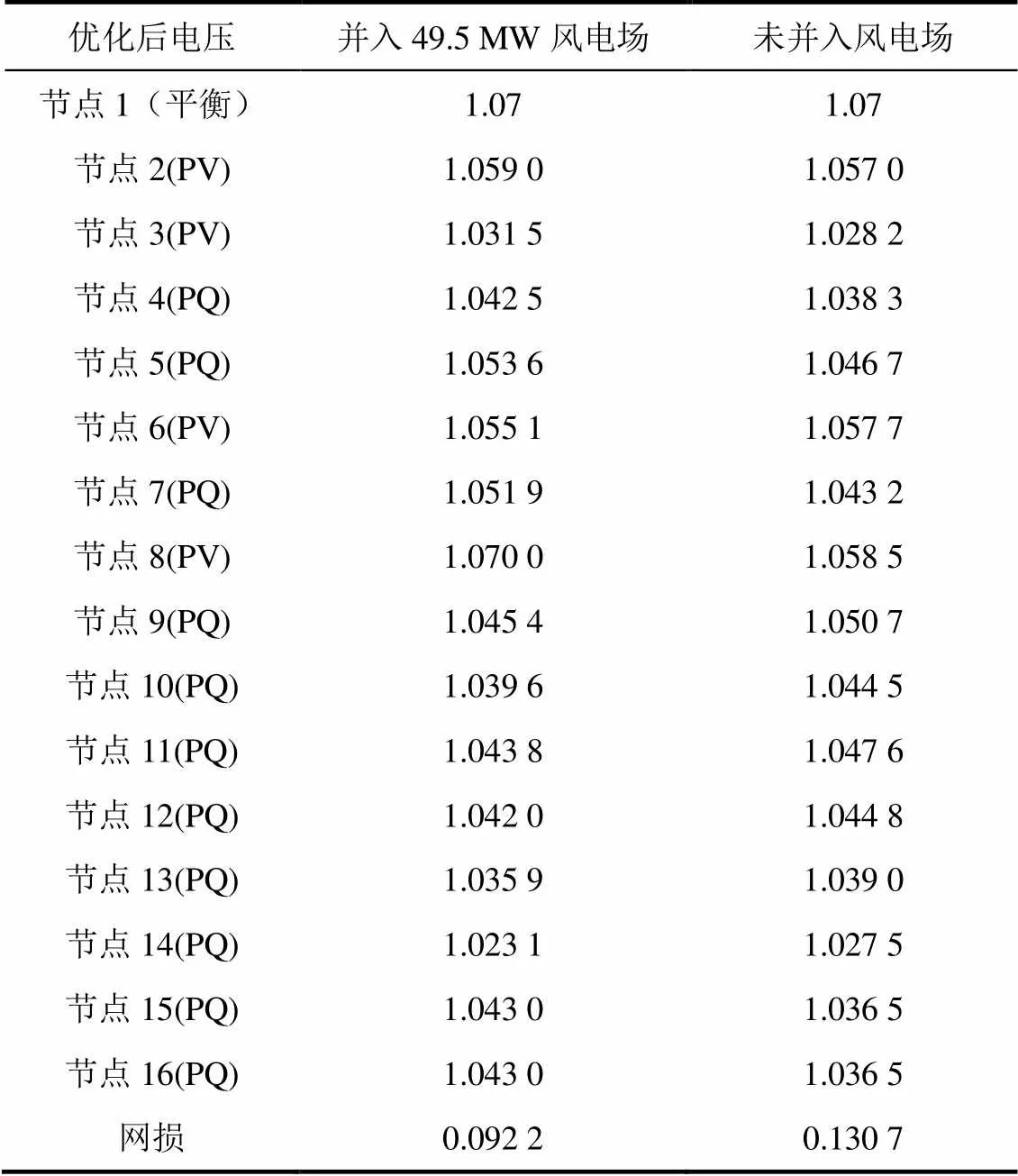
Table 3 Optimal voltage with/without wind farm

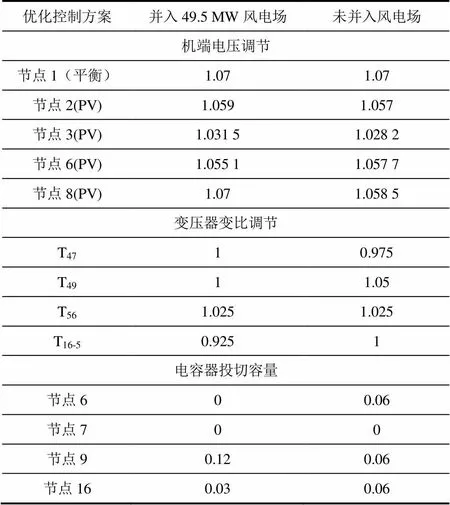
表4 并入/未并入风电场时优化控制方案

由算例的表和图可知：

(1) 从表1和表3可看出，风电场并入与否，系统无功优化之后得电网电压，都基本处于区间无功优化之后所得到的电压区间之内。

(2) 由图3和图4可以看出，在确定发电机出力情况和确定负荷情况下，未并入风电场系统的网损是0.130 7 p.u，并入风电场后，系统的网损为0.092 2 p.u，而区间无功优化的网损中点值为0.105 785 p.u。如果在未并入风电场之后，系统的负荷比较轻的话，系统的网损将会低于0.130 7 p.u；如果在并入风电场之后，负荷处于重载的情况下，系统的网损将高于0.092 2 p.u，因此基于区间算术的无功优化得到的趋优网损值在合理的范围之内。

(3) 由图2和表1可以看出，由本文所提的方法进行无功优化，节点电压都约束在区间[0.97,1.07]的范围之内，而且优化之后，网损的中点值较优化前减少4.869 6%。

因此，由上面的分析可以看出，本文所提的基于区间数的无功优化具有一定的合理性。

5 结论

针对电网运行过程中负荷、发电机被迫停运和并网分布式电源都具有不确定性，提出了一种基于区间数的无功优化方法，使得在计及不确定因素运行的情况下电网都能趋优运行。通过理论和算例验证表明，基于PSO的单个潮流断面无功优化得到的电压都基本包含于基于区间数的无功优化得到电压优化区间，而且区间无功优化的网损中点值也与单个潮流断面的优化网损相吻合。因此所提的基于区间数的无功优化模型在计及电网不确定性因素运行具有可行性，可以为考虑多种不确定因素下的电网无功优化提供一种有效的途径。另外，该优化控制方法可以用于日前调度计划安排，从总体上考虑未来一日内无功电压控制设备的调控情况，在达到日运行计划最优的同时能够避免设备的频繁操作。在网络建设、无功电源规划时也可以运用该方法来处理各种不确定因素。

[1] COVA B, LOSIGNORE N, MARANNINO P, et al. Contingency constrained optimal reactive power flow procedures for voltage control in planning and operation[J]. IEEE Trans on Power Systems, 1995, 10(2): 602-608.

[2] LIU M B, TSO S K, CHENG Y. An extended nonlinear primal-dual interior-point algorithm for reactive-power optimization of large-scale power systems with discrete control variables[J]. IEEE Trans on Power Systems, 2002, 17(4): 982-991.

[3] 张丽, 徐玉琴, 王增平, 等. 包含分布式电源的配电网无功优化[J]. 电工技术学报, 2011, 26(3): 168-174.

ZHANG Li, XU Yu-qin, WANG Zeng-ping, et al. Reactive power optimization for distribution system with distributed generators[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 168-174.

[4] 杨纶标, 高英仪. 模糊数学原理及应用[M]. 广州: 华南理工大学出版社, 2006.

YANG Lun-biao, GAO Ying-yi. Principle and application of fuzzy mathematics[M]. Guangzhou: South China University of Technology Press, 2006.

[5] 郭康, 徐玉琴, 张丽, 等. 计及光伏电站随机出力的配电网无功优化[J]. 电力系统保护与控制, 2012, 40(10): 53-58.

GUO Kang, XU Yu-qin, ZHANG Li, et al. Reactive power optimization of distribution network considering PV station random output[J]. Power System Protection and Control, 2012, 40(10): 53-58.

[6] 谢开贵, 肖畅. 计及负荷不确定性的无功优化模型与算法[J]. 电力系统保护与控制, 2011, 39(4): 18-22.

XIE Kai-gui, XIAO Chang. A reactive power optimization model and algorithm considering load uncertainty[J]. Power System Protection and Control, 2011, 39(4): 18-22.

[7] 刘志刚, 刘欢, 柳杰. 计及风电场概率模型的多目标无功优化[J]. 电力系统保护与控制, 2013, 41(1): 197-203.

LIU Zhi-gang, LIU Huan, LIU Jie. Multi-objective reactive power optimization considering wind farm probabilistic model[J]. Power System Protection and Control, 2013, 41(1): 197-203.

[8] 洪芦诚, 石立宝, 姚良忠, 等. 计及风电场发电功率不确定性的电力系统模糊潮流[J]. 电工技术学报, 2010, 25(8): 116-130.

HONG Lu-cheng, SHI Li-bao, YAO Liang-zhong, et al. Fuzzy modelling and solution of load flow incorporating uncertainties of wind farm generation[J]. Transactions of China Electrotechnical Society, 2010, 25(8): 116-130.

[9] 张丽, 徐玉琴, 王增平, 等. 包含分布式电源的配电网无功优化[J]. 电工技术学报, 2011, 26(3): 168-174.

ZHANG Li, XU Yu-qin, WANG Zeng-ping, et al. Reactive power optimization for distribution system with distributed generators[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 168-174.

[10] 邓威, 李欣然, 李培强, 等. 基于互补性的间歇性分布式电源在配网中的优化配置[J]. 电工技术学报, 2013, 28(6): 216-225.

DENG Wei, LI Xin-ran, LI Pei-qiang, et al. Optimal allocation of intermittent distributed generation considering complementarity in distributed network[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 216-225.

[11] TOMSOVIC K. A fuzzy linear programming approach to the reactive power/voltage control problem[J]. IEEE Trans on Power Systems, 1992, 7(1): 287-293.

[12] 张焰, 陈章潮. 计及不确定性的模糊交流潮流计算方法[J]. 电网技术, 1998, 22(2): 20-22.

ZHANG Yan, CHEN Zhang-chao. Algorithm of AC fuzzy load flow incorporating uncertainties[J]. Power System Technology, 1998, 22(2): 20-22.

[13] 刘秋野, 张化光, 刘兆冰. 配电网模糊潮流计算方法及其收敛性研究[J]. 中国电机工程学报, 2008, 28(10): 46-50.

LIU Qiu-ye, ZHANG Hua-guang, LIU Zhao-bing. Fuzzy flow calculation in power distribution system and its convergence[J]. Proceedings of the CSEE, 2008, 28(10): 46-50.

[14] 王德人, 张连生, 邓乃扬. 非线性方程的区间算法[M]. 上海: 上海科学技术出版社, 1986.

WANG De-ren, ZHANG Lian-sheng, DENG Nai-yang. Interval algorithm for nonlinear equations[M]. Shanghai: Shanghai Science and Technology Press, 1986.

[15] 裴爱华, 刘明波, 张弛. 考虑负荷不确定性的区间潮流计算方法[J]. 电力系统及其自动化学报, 2004, 16(6): 24-28.

PEI Ai-hua, LIU Ming-bo, ZHANG Chi. Interval algorithm for power flow calculation with uncertain load[J]. Proceedings of the CSU-EPSA, 2004, 16(6): 24-28.

[16] 王成山, 王守相. 基于区间算法的配电网三相潮流计算及算例分析[J]. 中国电机工程学报, 2002, 22(3): 58-62.

WANG Cheng-shan, WANG Shou-xiang. Distribution three-phase power flow based on interval algorithm and test results[J]. Proceedings of the CSEE, 2002, 22(3): 58-62.

Reactive power optimization based on interval arithmetic with distributed power grid

ZHANG Yong-jun, SU Jie-he, YI Ying-qi

(School of Electric Power, South China University of Technology, Guangzhou 510640, China)

Inorder to solve the uncertainty of the output of distributed power and the effects of load fluctuation, this paper presents a reactive power optimization method based on interval for the grid with distributed power. First, the concepts of interval number and interval arithmetic are introduced and the interval power flow is established. Then, objective function and constraint conditions of interval reactive power optimization model with distributed power are established, and the steps of solving the model with PSO are given. Finally, a modified IEEE 14 node system is simulated through Matlab and a certain power flow for reactive power optimization proves the correctness of the proposed algorithm.Simulation results shows that it can make the grid work in near-optimal state with taking into account the uncertainty of the grid. This work is supported by National High-tech R&D Program of China (863 Program) (No. 2012AA050209) and National Natural Science Foundation of China (No. 51147006).

distributed power; reactive power optimization; interval power flow; PSO

TM561

A

1674-3415(2014)15-0021-06

2013-10-23；

2014-03-20

张勇军(1973-)，男，博士，教授，主要从事电力系统无功优化和电压稳定、电力系统可靠性与规划等研究；E-mail：zhangjun@scut.edu.cn

苏杰和(1988-)，男，硕士生，主要从事电力系统无功优化与无功电压控制研究；

羿应棋（1990-)，男，硕士生，主要从事电力系统无功优化与无功电压控制研究。

863计划（2012AA050209）；国家自然科学基金资助项目（51147006）