一种远海岛(礁)区域高程基准转换的新方法

郭忠磊，滕惠忠，赵俊生，邓凯亮，黄辰虎

(1. 大连舰艇学院 海洋测绘系，辽宁 大连 116018； 2. 天津海洋测绘研究所，天津 300061)

一、引 言

国内学者大多采用传递的方式将大陆的高程基准传递到海岛上，李建成比较分析了静力水准法、动力水准法及常规大地测量法3种方法的优缺点[1]；章传银等研究了基于EGM2008模型的高程基准统一与转换方法[2-3]；张利明研究了利用基于重力等位面的方法进行跨海高程传递的问题[4]。理论上，在海洋区域平均海面与(似)大地水准面是重合的，由于海面地形的存在，使得二者存在差异。在海洋测绘中，海图深度基准面相对于平均海面而确定,海岛(礁)区域高程基准转换的目的是实现海岛礁地形图与海图的拼接。海岛(礁)区域高程基准以1985国家高程基准起算，海图与岛(礁)地形图的拼接将会面临基准偏差难以确定的问题。按照《海道测量规范》(GB 12327—1998)[5]规定：远离大陆的岛礁地形测绘高程基准一般采用当地平均海面。

在缺少甚至无验潮资料的岛礁区域，如何精确构建岛礁区域的平均海面模型是实现高程基准转换的关键。基于不同卫星测高模型，国内外学者进行了广泛的应用与研究：王正涛等利用法国的CLS01测高平均海面模型研究了海洋重力似大地水准面与区域测高似大地水准面的拟合问题[6]；孙翠羽以武汉大学的WHU2009平均海面模型及3个验潮站的观测数据作为控制条件，建立了渤海湾基于CGCS2000参考椭球的海洋垂直参考系统[7]。Yong cun Cheng基于DNSC08MSS比较了有潮汐数据与无验潮数据区域的海面变化情况[8]；Per Knudsen基于GOCE数据及DTU10MSS(DTU10 mean sea surface)重新构建了新的海面动态地形DTU12MDT，并以此计算了海洋环流[9]。已有的应用实践说明了现有卫星测高模型的高精度和广泛适用性。

本文选择丹麦空间技术中心最新发布的高精度、高分辨率平均海面模型——DTU10MSS，采用最小二乘(least squares, LS)与全最小二乘(total least squares, TLS)二次多项式拟合方法构建岛礁区域的平均海面模型，实现GPS测量的大地高转换为当地平均海面起算的高程值，并在某远海岛(礁)区域进行了计算比较。计算结果说明在远离大陆的海岛(礁)区域进行高程转换时可采用该卫星测量模型，转换精度满足不大于1∶5000比例尺地形图测绘的高程精度要求。

二、 曲面拟合模型

拟合通常采用两种方式即插值方式和逼近方式来实现。两者的共同点是均利用曲面上或接近曲面的一组离散点，寻求良好的曲面方程。两者主要的区别是：插值方式得到的方程所表示的曲面全部通过这组数据点；而逼近方式只要求在某种准则下，其方程表示的曲面与这组数据点接近即可。卫星测高模型即为一个格网化均匀分布的离散数据点，二次多项式曲面拟合法可以在拟合点分布均匀的情况下构建平均海面变化趋势，二次多项式模型为

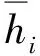
式(1)中有6个参数，因此参与拟合的格网点至少是6个。当点多于6个时，仍列出相应的误差方程，根据最小二乘原理求解参数的解。

1. 最小二乘法参数解算

最小二乘法准则是一种逼近理论，也是采样数据进行拟合时最常用的一种方法。曲面一般不通过已知数据点，而是根据拟合的曲面在取样处的值与实际值之差的平方和达到最小求得，它的主旨思想就是实测数据与真实值之间的偏差平方和达到最小。误差方程为

V=AX-L

(2)

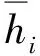
在式(3)求解过程中，将卫星测高的格网点视为独立等价权的观测值。

2. 全最小二乘参数解算

理论上，总体最小二乘是比最小二乘更合适的拟合方法。该方法同时顾及观测向量L和设计矩阵A中的误差，使得拟合得到的趋势面模型能够更好地反映平均海面的变化趋势。

全最小二乘准则是1980年Gohb[10]等人引入的。其误差模型为

L-V=(A-EA)X

(4)

式中，EA为设计矩阵的误差。

从几何的观点看线性拟合问题：对于2维数据，即寻找1维的一条直线近似描述它们的关系；对于3维数据来说，寻找2维的一张平面来近似描述它们的关系。假设有p+1维空间中一组数据，要用p维子空间(直线、平面或超平面)来拟合p+1维空间中的数据，因此这是数值分析上的一个降秩逼近问题，一般可选择奇异值分解(SVD)方法解算

[A;L]=UΣVT

(5)

式中，U、V为酉矩阵；Σ为对角阵，σi为[A;L]的奇异值，σ1≥σ2≥…≥σm+1。

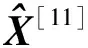
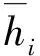
三、DTU10MSS模型

2010年丹麦空间技术研究中心发布了分辨率为1′×1′的DTU10模型，它是对DNSC08模型的改进，DTU10MSS与DNSC08MSS的偏差不超过3 cm[12]。DTU10是基于多源测高卫星数据建立的测高模型，融合的数据包括17年的TOPEX/Poseidon及后续卫星Jason-1、ERS、Envisat、Geosat-Follow-On(GFO)。数据处理采用最小二乘配置构建分辨率为1′×1′的全球平均海面模型。DTU10与其他测高模型特点比较见表1。

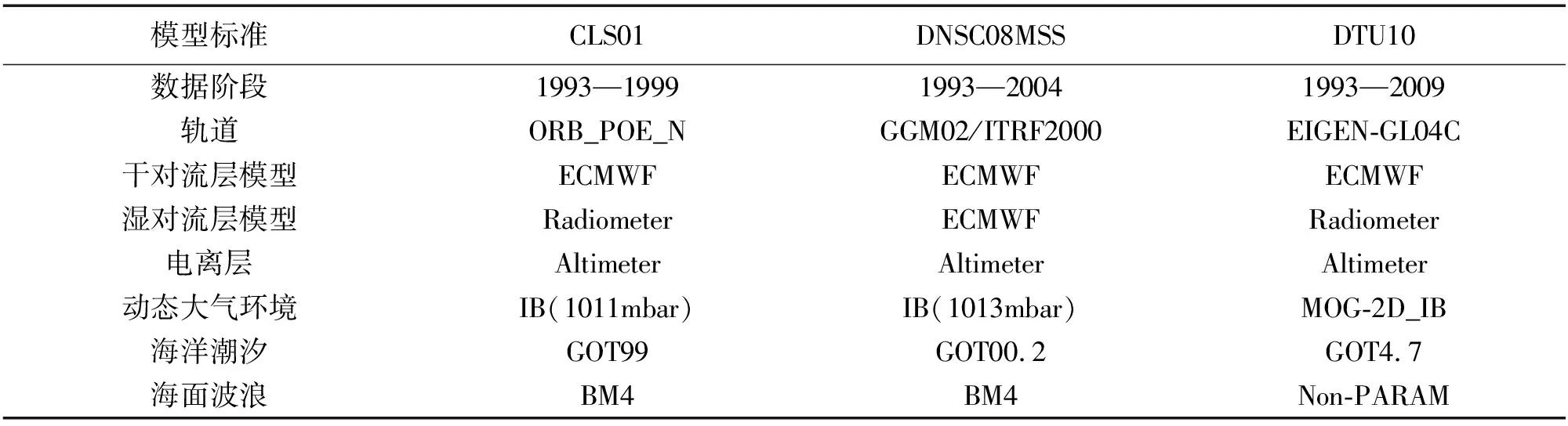
表1 CLS01、DNSC08MSS 、DTU10比较

从表1可以看出，DTU10模型采用的数据周期时间更长，数据后处理采用了新的海洋潮汐预报模型、动态大气环境模型、海面波浪模型，而这3项改正是对测高精度影响最大的误差源。

卫星测高技术虽然可以持续提供广阔海面上的潮汐信息，但是在浅水区域，测高计的雷达回波会受到陆地反射信号的干扰，再加上近岸海洋环境较为复杂，在近岸几十千米的浅海区域及岛屿周围，测高数据都难以取得较好的精度。试验数据为某远离大陆海区(距离大于100 km)的卫星测高数据，该海域的岛礁面积小，最大岛礁范围不超过2倍的格网分辨率，而且岛屿近岸处海水的深度变化剧烈，水深普遍大于20 m。因此，卫星测高数据在该区域具有良好的适用性。

四、试验分析

由于试验区内的岛屿分布零散、面积小，模型拟合时根据岛屿的地理分布与大小划定拟合半径。选择4个岛屿，分别采用LS拟合与TLS拟合建立对应岛屿的平均海面模型，利用该4个区域的GPS/水准测量结果作为检核数据。试验区岛屿分布如图1所示，试验比对结果见表2。

图1 岛屿分布

表2 LS与TLS在不同区域的拟合值与实测值比较 m

从表2可以看出，无论是LS算法的拟合结果还是TLS算法的拟合结果，与实测值存在较大偏差(最大0.844 m，最小0.406 m)。

通过分析发现，拟合结果存在的偏差是系统性的，主要原因是DTU10模型与WGS-84坐标系采用的椭球基准不一致。DTU10模型是基于多源测高卫星数据建立的，采用的测高卫星的轨道参数见表3，数据处理时参考基准统一到T/P卫星上。因此，在应用卫星测高模型进行基准的转换时必须改正参考椭球基准不同造成的高差。高差改正公式为

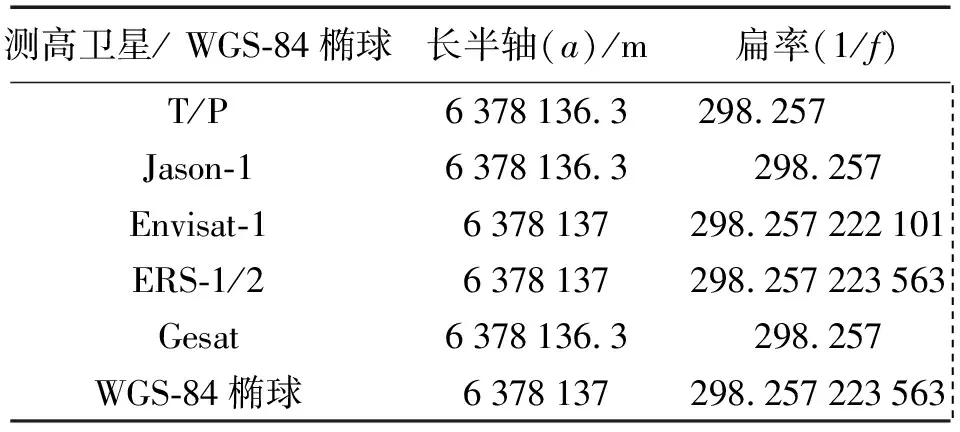
表3 不同测高卫星与WGS-84坐标系采用椭球参数

表4 纬度与高差关系

由表4可以看出，在不同纬度地区，对于不同的测高卫星，椭球参数、椭球定位和定向的差别可以导致测高数据观测值的差距达到0.70 m左右，是一个系统偏差。

椭球面与大地水准面并不平行性，还要考虑增加一项垂线偏差改正。国内学者张有广等利用TOPEX/POSEIDON卫星测高数据对垂线偏差造成的海面高误差进行了分析，认为误差在毫米量级，个别点的误差超过1 cm[13]；邢乐林通过对测高数据增加垂线偏差改正建立新的卫星测高模型，与CLS01模型比较，也证明垂线偏差造成的误差量级比较小，大部分误差为毫米量级[14]。因此，在应用DTU10MSS测高数据模型时，忽略垂线偏差产生的误差。表5为基准统一后的拟合结果。

表5 DTU10MSS基准统一后计算结果比较 m

从表5可以看出，TLS算法拟合结果整体优于LS算法拟合结果，即采用TLS算法能够更好地拟合平均海面的变化趋势；从实测点与拟合点的比较可看出，统一基准后模型仍有较大的误差，最大为0.294 m，考虑海面地形的动态差异性，在中小比例尺测图时，该误差可以接受。

在D区域出现较大异常，主要原因是D区域的比对点为一验潮站水准点，验潮观测的数据受地形影响，与由模型推算的结果存在偏差；拟合值与实测值之间误差的存在也说明卫星测高模型面临近岸海域海水局部动力环境，如水深变化、海岸形状、海底地形、海流河流、岛屿分布、潮流等影响，目前已有的全球海面地形模型用于近岸海域存在系统差的几率较大[15]。

五、结束语

远离大陆的海岛(礁)分布零散，数量众多，如果采用常规测量手段，实现海岛礁的地形测量任务繁重。尤其是在远离大陆的海岛(礁)上一般需要建立验潮站进行水位联测，确定当地的高程起算面，更是增加了测量的周期与作业成本。在海洋测绘中，海岛礁区域高程基准转换的主要目的是实现海岛礁地形图与海图的拼接，海图深度基准面相对于平均海面确定。因此，在海岛礁地形测量中的高程应选择平均海面起算。在缺少甚至无验潮数据的远离大陆海岛(礁)区域，采用高精度、高分辨率的测高模型——DTU10MSS可以实现大地高到平均海面高的转变，转换精度满足中小比例尺岛礁地形测量对高程基精度的要求。由于实地测量的检查点数据较少，难以准确反映出海面地形及其他因素的影响。今后将会通过采集更多的检查点进行比对，分析海面地形的影响特点。

参考文献：

[1] 李建成,姜卫平.长距离跨海高程基准传递方法的研究[J]．武汉大学学报:信息科学版，2001，26(6):514-517.

[2] 章传银,郭春喜,陈俊勇,等.EGM2008 地球重力场模型在中国大陆适用性分析[J].测绘学报，2009,38(4):283-289.

[3] 柯宝贵,章传银,张利明.远离大陆海岛的高程传递[J].测绘通报,2011(12):3-4.

[4] 张利明.与陆地一致的海岛(礁)高程传递方法:中国,20100198624[P].2010-06-12.

[5] 国家质量技术监督局.GB 12327—1998海道测量规范[S].北京：中国标准出版社,1999.

[6] 王正涛,李建成,晁定波.海洋重力似大地水准面与区域测高似大地水准面的拟合问题[J].武汉大学学报：信息科学版,2005,30(3):234-237.

[7] 孙翠羽．海洋无缝垂直基准面建立方法研究—以渤海海域为例[D]．青岛：山东科技大学，2011.

[8] CHENG Y C,ANDERSEN O B,KNUDSEN P. Integrating Non-Tidal Sea Level Data from Altimetry and Tide Gauges for Costal Sea Level Prediction[J]. Advances in Space Research,2012,50(8):1099-1106.

[9] KNUDSEN P,BINGHAM R, ANDERSEN O, et al. Enhanced Mean Dynamic Topography and Ocean Circulation Estimation Using GOCE Preliminary Models[C]∥Proceedings of 4th International GOCE User Workshop.Munich,Germany:ESA,2011.

[10] GOLUB H G, Van LOAN F C. An Analysis of the Total Least Squares Problem[J]. SIAM (Soc. Ind. Appl. Math.) J. Numer. Anal,1980,17(6):883-893.

[11] FELUS Y A. Application of Total Least Squares for Spatial Point Process Analysis[J]. Journal of Surveying Engineering,2004,130(3):126-133.

[12] ANDERSEN O, KNUDSEN P. DNSC08 Mean Sea Surface and Mean Dynamic Topography Models[J].Journal of Geographysical Research:Oceans(1978—2012)，2009，114(11):493-496.

[13] 金涛勇,李建成，姜卫平，等.基于多源卫星测高数据的新一代全球平均海面高模型[J].测绘学报,2011,40(6)：723-729.

[14] HWANG C．Analysis of Some Systematic Errors Affecting Altimeter—Derived Sea Surface Gradient with Application to Geoid Determination over Taiwan[J].Journal of Geodesy,1997,71(2):113-130.

[15] 陈俊勇,李建成.我国海域大地水准面的计算及其与大陆大地水准面拼接的研究和实施[J].地球物理学报，2003，46(1)：31-35.

[16] 张有广,张杰，纪永刚.TOPEX/Poseidon卫星测高的垂线偏差修正[C]∥第十四届全国遥感技术学术交流会论文集.北京：中国海洋学会，2003.

[17] 邢乐林,刘冬至，金涛勇，等.垂线偏差对用卫星测高数据建立海面高模型的影响[J].大地测量学与地球动力学,2007,27(2):61-63.