响应面中心组合设计对高填特种纸浆料助滤系统的优化
卫晓林 李杰辉,3 羡羽佳 庄金风,*
(1.中国制浆造纸研究院,北京,100102;2.制浆造纸国家工程实验室,北京,100102;3.天津科技大学,天津,300457)
如今纤维原料紧缺且价格昂贵,为了节约纤维、降低成本,生产高填纸已成为众多造纸企业求生存、求发展的选择之一[1]。填料含量的增加不仅会降低纸张强度性能,还会影响纸张的抄造性能[2]。为了提高高填纸浆料中细小组分的留着和浆料在湿部的脱水能力,在造纸生产过程中应选用合适的助留助滤体系。本研究以高填特种纸浆料为对象,对其助滤系统的应用进行了优化研究。首先通过单因素实验(只控制助剂用量)对单元和双元助滤系统进行了筛选,然后从助剂用量、搅拌转速、反应时间等方面考虑,采用响应面法的中心组合设计利用SAS统计软件对其进行了进一步优化,得出了实验模型。最后,对所得模型进行了实验验证。

表1 实验采用的各种助剂及相关参数
1 实 验
1.1 实验原料与仪器
浆料:高填特种纸浆料,由木浆纤维、填料与其他助剂以一定比例在实验室配制而成。
化学品:实验所用化学品均由巴斯夫公司提供,各参数指标如表1所示。
仪器:比过滤阻力仪为本实验室自制。
1.2 实验方法
1.2.1滤水性的测定
本研究选用比过滤阻力(Specific Filtration Resistance,SFR,单位m/g)来评价浆料的滤水性。比过滤阻力描述的是浆料的一种内在特性,它与仪器的几何形状无关,其数值表示水在一定温度下以单位流速通过单位质量自然形成的浆料滤饼的阻力。比过滤阻力起源于Darcy定理,是从对不可压缩介质的滤水性的研究发展起来的。W. L. Ingmanson等人认为,Darcy定理也可用于可压缩植物纤维层的过滤,由于浆料的总过滤阻力为滤网的阻力和纤维垫层的阻力之和,在此基础上,提出了适用于浆料的过滤方程[3],公式如下:
(1)

(2)
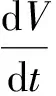
国内已有学者对采用比过滤阻力评价浆料滤水性进行过论述[3- 6],但其仅仅是综述性概述,未详细描述测试所用仪器装置。本研究采用自制的比过滤阻力仪测定浆料的SFR,并对助滤系统的优化设计进行研究。测定过程为:称取含3.0 g绝干浆料,按所需条件添加助剂;关闭比过滤阻力仪阀门,向测量筒中加水,使水刚好浸没过铜网;将配制好的浆料倒入测量筒中;打开阀门,使浆料在无外界干扰的自然过滤条件下形成一层均匀的滤饼;而后关闭阀门,放入限流板,沿限流板导杆向测量筒中加水,使其产生溢流,从而保证测量筒中液位恒定;打开阀门,收集滤液60 s,然后测定滤液质量和温度;干燥滤饼并称其质量;将各参数带入公式计算SFR。
1.2.2助滤系统的选择
从助剂用量和种类两个方面考查了助剂对浆料滤水性的影响。采用单元助滤系统的实验步骤为:在低速搅拌过程中向浆料中添加CPAM,反应60 s后测定浆料的SFR;采用双元助滤系统时的实验步骤(见图1)为:在低速搅拌过程中向浆料中添加CPAM,反应60 s后提高搅拌转速搅拌15 s,然后降低搅拌转速,再向浆料中添加第二种助剂(膨润土或高支化PAM),反应20 s后测定浆料的SFR。根据SFR选出最佳助滤系统,而后采用响应面法优化浆料SFR的影响因素。

图1 滤水性实验的基本操作过程
1.2.3响应面中心组合设计
根据前期实验结果选出最佳助滤系统,然后再从助剂用量、搅拌转速和反应时间等方面对其进行优化。优化过程采用响应面中心组合设计法,该方法方便简单,能得出自变量与变量之间函数关系的回归方程[7- 8]。在本研究中,每个因素取5个水平(-2,-1,0,+1,+2),按方程xi=(Xi-X0)/X对自变量进行编码。其中,xi为自变量的编码值,Xi为自变量的真实值,X0为实验中心点处自变量的真实值,X为自变量的变化步长。据此列出实验表,根据相应的实验表进行实验后,对数据进行二次回归拟合,得到包括一次项、平方项和交互项的二次方程,再分析各因素的主效应和交互效应,最后在一定水平范围内求取最佳值。
本实验利用SAS软件设计分析实验,由方差分析得出各因素的主效应、交互效应以及该实验的预测模型(本实验将置信概率规定为95%)。总共需进行31次(N=2n+2n+n0,其中n为影响因素的个数,n=4;n0为中心点的实验个数,n0=7)实验。假设实验中的影响因素分别为X1、X2、X3、X4…,则预测模型的二次方程式如下:
2 结果与讨论
2.1 助滤系统的筛选
图2为不同助滤系统对浆料滤水性的影响。由图2可知,单元助滤系统效果较差,对浆料滤水性改善效果不明显,而且,4种CPAM的效果差异也不大。与单元助滤系统相比,双元助滤系统的助滤效果比较显著。
根据助剂对浆料滤水性的作用效果可知,CPAM用量约为0.015%时,系统滤水性的提高趋于平缓,而此时3#CPAM+高支化PAM的滤水性提高最明显,故从这12种组合中选择3#CPAM+高支化PAM系统进行下一步实验。除助剂种类外,助剂用量、加入点等工艺条件也对浆料留着、滤水及成纸匀度有显著影响。在后续的影响因素优化实验中,本研究通过控制搅拌转速和反应时间来模拟研究助剂在生产线上的加入位置。
2.2 中心组合设计
在前期实验的基础上,以SFR为响应值,对CPAM(3#,下同)用量、搅拌转速、反应时间、高支化PAM用量等4个因素的影响进行了考察,每个因素取“-2、-1、0、+1、+2”5个水平。中心组合设计中的因素与水平设计如表2所示。
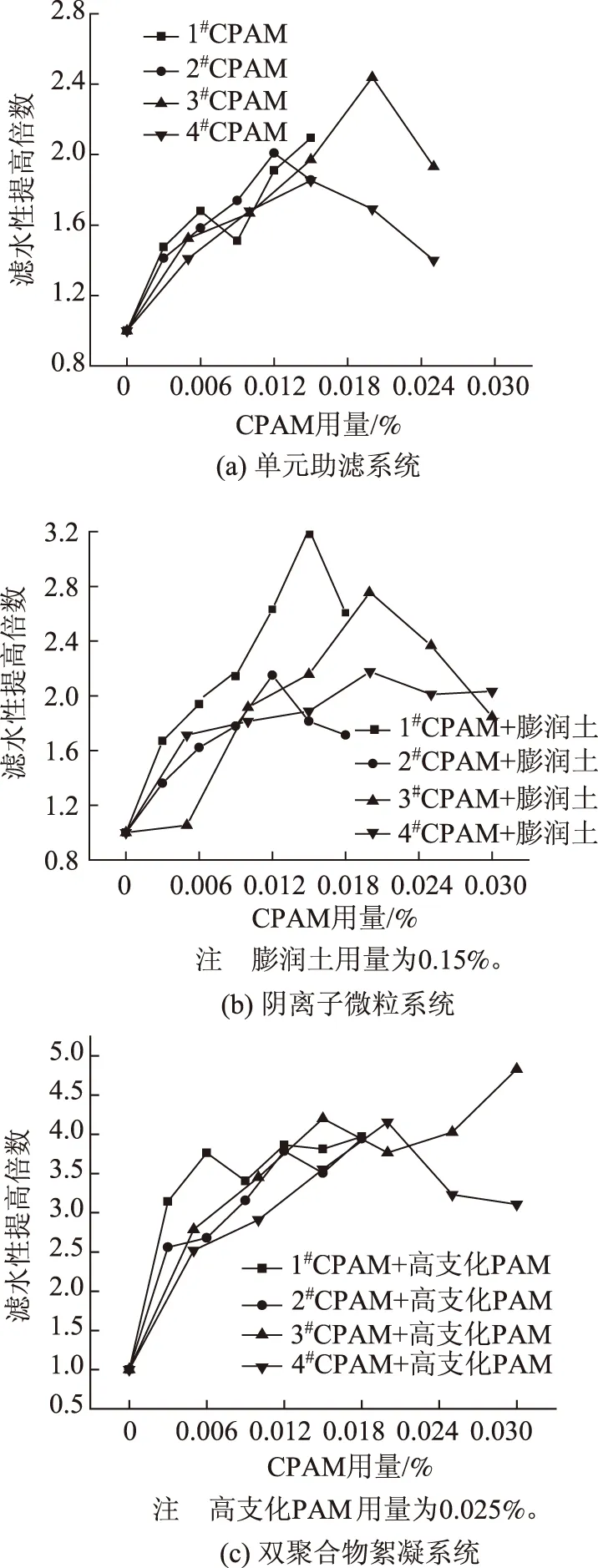
图2 不同助滤系统中助滤剂用量对滤水性的影响
表2中心组合设计中四因素五水平的设计

影响因素 五水平设计a(-2)-10+1A(+2)X1CPAM用量/%0.0050.0100.0150.0200.025X2搅拌转速/r·min-125050075010001250X3反应时间/s306090120150X4高支化PAM用量/%0.010.020.030.040.05
2.2.1响应面分析方案及结果
由响应面中心组合设计法设计实验,实验组数N=31,其中设置7个虚拟列(即零点列,也称为中心点列)用来考察实验误差,以比过滤阻力(SFR)Y1作为响应值,实验设计及结果见表3。
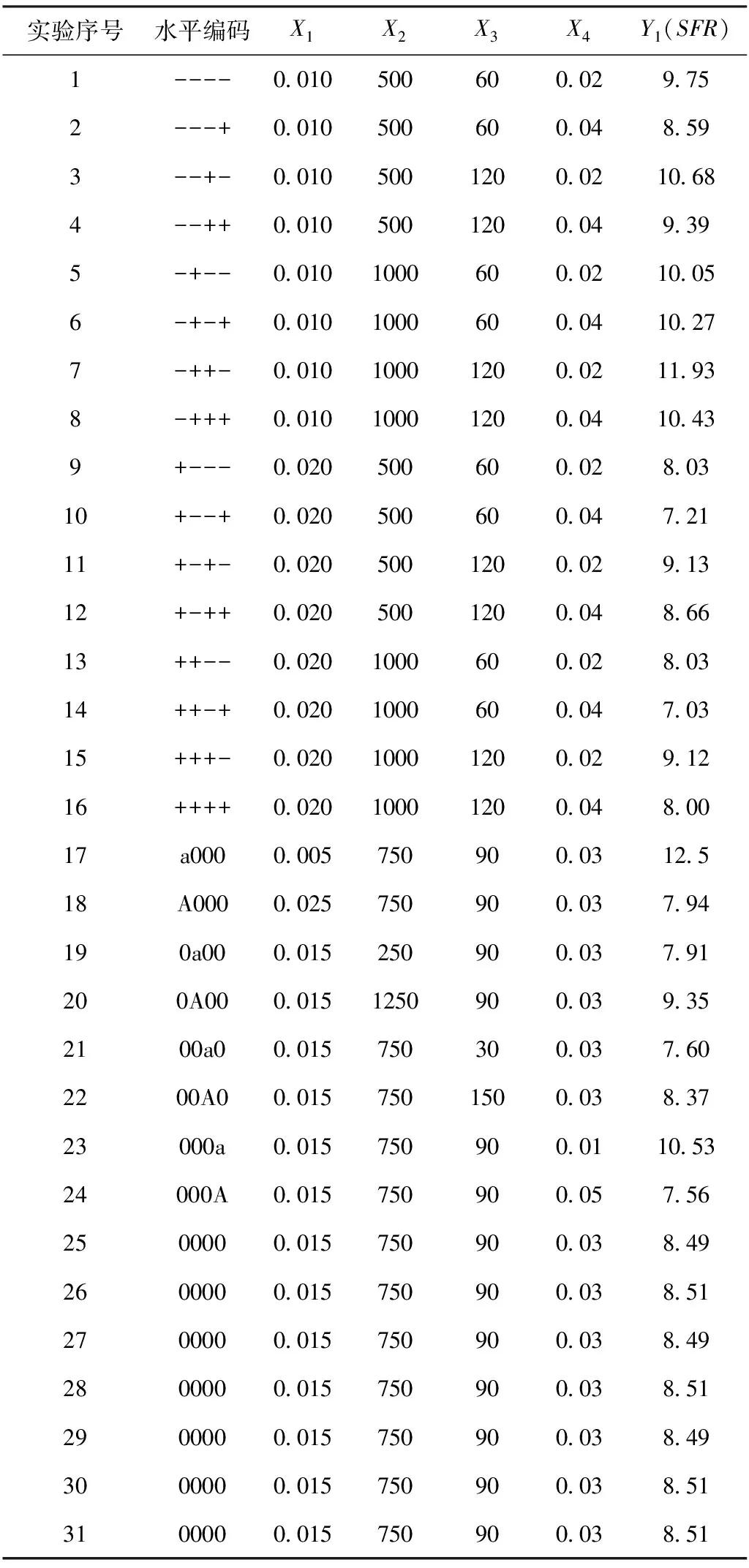
表3 响应面中心组合实验设计及结果
用SAS统计软件包对表3中的实验数据进行方差分析,所得结果如表4所示。各因素经回归拟合后得出如下回归方程:
Y1=8.5016-1.0444x1+0.2623x2+0.4138x3-
其相关系数R2=0.9534,实验值与预测值拟合性良好。

表4 回归方程方差分析

图3 置信概率为95%滤水性实验的预测曲线
由表4可看出各因素对浆料滤水性影响的显著性。其中,α值越小,其影响越显著;当α<0.05时,表明其影响显著;当α<0.01时,表明其影响极其显著;α值越大,其影响越不显著,当α>0.05时,表明其影响不显著。由此可知,各因素对滤水性影响的显著性水平的大小依次为:CPAM用量>高支化PAM用量>反应时间>搅拌转速;而不同因素之间的交互效应对滤水性的影响都不显著。整体模型的α<0.01,表明该二次方程模型有较高的适用性。
图3显示了在置信概率为95%时滤水性实验的预测曲线。虚线部分表示曲线的正负误差范围。由图3可知,随CPAM用量(X1)的增加,SFR首先逐渐减小,但当用量过大时,SFR略微增大;随高支化PAM用量(X4)的增加,SFR呈逐渐减小的趋势;而增大搅拌转速(X2)会给浆料滤水带来不良影响;延长反应时间(X3)也会使浆料滤水性变差。
2.2.2因素间的交互影响
采用SAS软件分析响应面数据的结果见图4。图4直观地给出了在2个因素的水平固定在中心点的情况下其余2个因素交互效应的响应面的3D分析图。由X1(CPAM用量)和X2(搅拌转速)对Y1(SFR)的响应曲面图(见图4a)可看出,固定X2,Y1随X1的增加而减小,达到最低值后又略微增大;固定X1,Y1随X2的增加而增大。故在助剂添加过程中需同时关注CPAM用量和剪切力对絮聚体的影响。
2.2.3回归模型的验证
为了验证回归方程的准确性,额外进行了6组实验(见表5),然后将实验结果与方程计算结果进行对比。图5为实验值与模型值的对比。由图5可知,实验值与模型值具有较好的一致性。因此,可通过该模型计算得出最佳工艺条件的编码值,CPAM用量、搅拌转速、反应时间及高支化PAM用量的编码值分别为0.3、1、-2.3、0.2,由此推算出其真实值分别为0.016%、1000 r/min、21 s及0.032%,相应的比过滤阻力为6.9 cm/g。

表5 模型验证实验设计
另外,采用SAS软件中的响应面设计法也可得出不同因素在不同水平下的等高线图(见图6)。由图6可知,选定X1与X2之间交互效应的等高线图为例(X3与X4的水平分别固定为+1、-1),由此等高线图可以直观地得知图中任意点的因素、水平与响应值的具体数值及其相互关系,对此可根据需求确定实验条件。
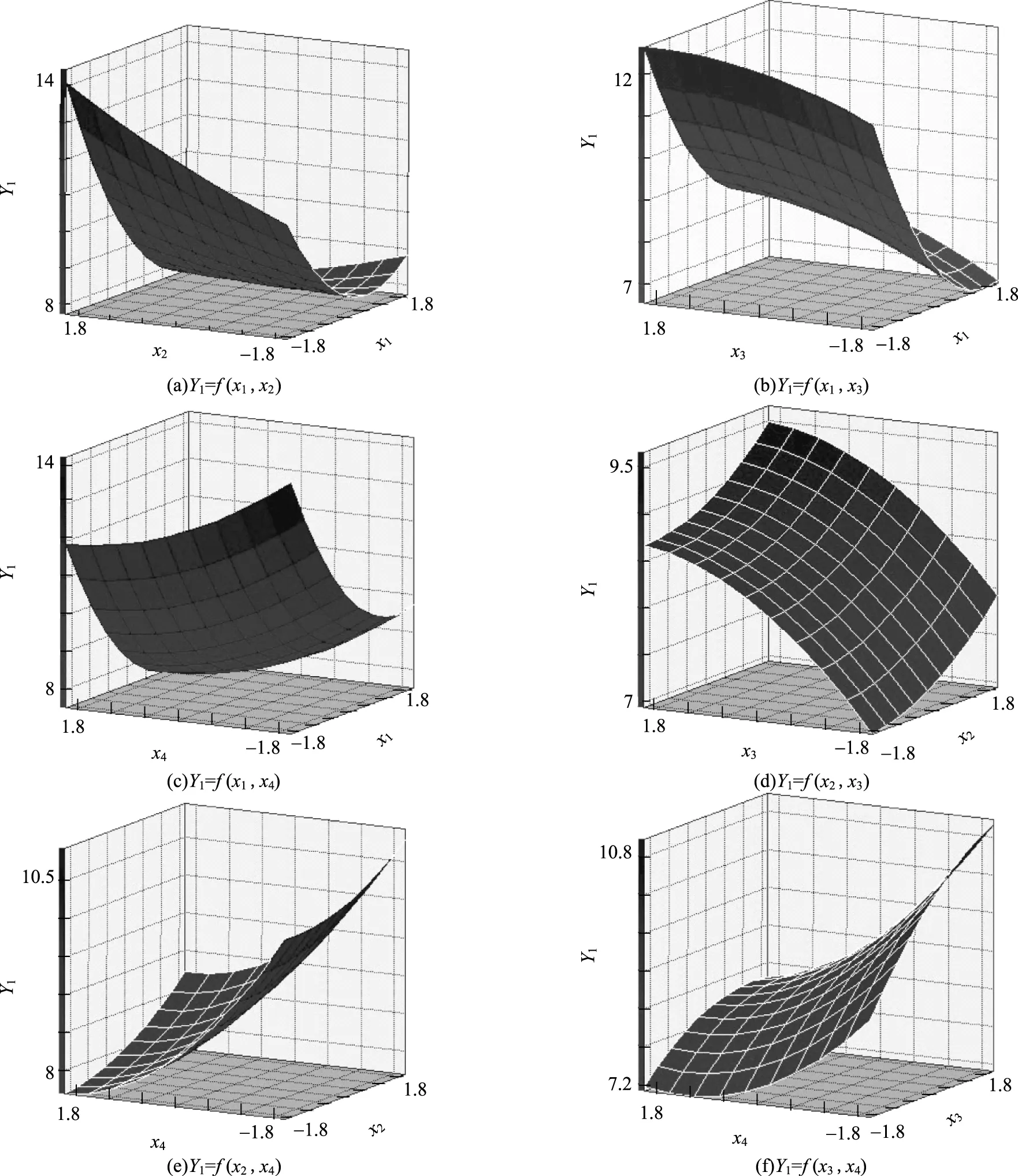
图4 响应面3D分析图
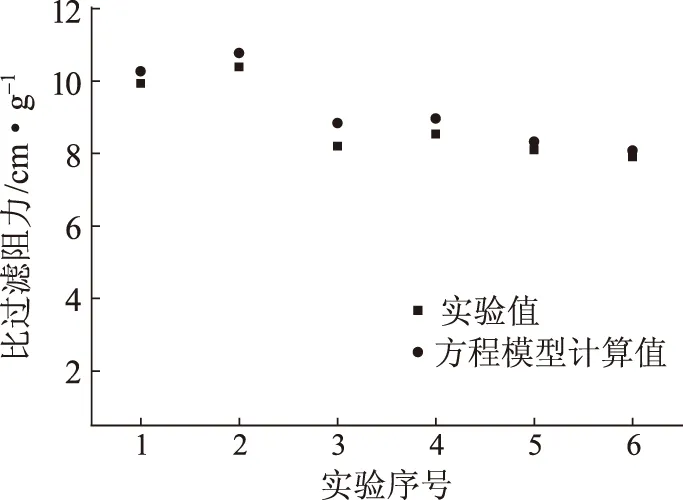
图5 模型验证实验的实验值与计算值

图6 Y1=f(x1,x4)的响应面等高线图
3 结 语
本实验首先通过一系列单因素实验筛选出了最佳助滤系统,采用响应面中心组合设计从助剂用量、搅拌转速、反应时间等方面优化了助滤系统的使用工艺条件,得出了实验模型,然后,对所得实验模型进行了验证。验证结果表明,模型计算值与实验值吻合。由该模型计算出工艺条件的具体数值,分别为CPAM用量0.016%、搅拌转速1000 r/min、反应时间23 s及高支化PAM用量0.032%。同时也可根据实验需求,通过等高线图来选择合适的使用工艺条件。
参 考 文 献
[1] 姚晓红. 高填料纸张制备技术及其性能研究[D]. 杭州: 浙江理工大学, 2012.
[2] 刘 忠. 造纸湿部化学[M]. 北京: 中国轻工业出版社, 2010.
[3] 施志超, 徐立新. 评价和改善纸浆滤水性能的几种方法[J]. 上海造纸, 2005, 36(4): 22.
[4] 梁 云, 陈克复. 用比过滤阻力评价纸浆滤水性能[J]. 中国造纸学报, 1999, 14: 110.
[5] 梁 云, 陈克复. 用比过滤阻力系数来评价纸浆滤水性能[J]. 广东造纸, 1998(2): 27.
[6] 陈 韡. 纸浆絮聚特性可视化及过滤阻力的研究[D]. 天津: 天津轻工业学院, 2000.
[7] Sang Yizhou, McQuaid Michael, Englezos Peter. Pre-flocculation of precipitated calcium carbonate filler by cationic starch for highly filled mechanical grade paper[J]. BioResources, 2012, 7(1): 354.
[8] Sang Yizhou, McQuaid Michael, Englezos Peter. Optimization of chemical use for highly filled mechanical grade papers with precipitated calcium carbonate[J]. BioResources, 2011, 6(1): 656.

