基于改进遗传算法的海上油气田优化气举研究
赵春立 朱 颐 李禹呈 杨 志 周 倩
(1.西南石油大学, 成都 610500; 2.川庆钻探工程有限公司川西钻探公司, 成都 610000;3.西南油气田分公司川中油气矿, 四川 遂宁 402660; 4.西南油气田分公司蜀南气矿,四川 泸州 642450)
压缩机组作为气举采油的动力源,直接影响气举采油系统的规模。由于维护要求或故障原因,部分压缩机通常不能正常运转,机组总供气量降低最终影响到压缩机出口压力,这时一些井就需要关闭,而且需要判断关闭哪些井对总产量影响最小。当注气压力低于一些井的最小注气压力时,可能造成气举井的间喷。间喷带来的压力和流速振荡将降低系统总产量,造成设备的严重扰动,甚至引发系统停机。另外,井口压力峰值还会造成分离器内压力过高、压缩系统过载以及由于流体压力振荡所产生的设备疲劳问题。
为避免以上问题,必须对每口气举井的注气速度进行优化,确定每口井最佳气举注气速度是一个组合优化问题。遗传算法作为一种启发式搜索方法,其固有特点是优化解不依赖初始条件且容易考虑限制条件。此算法广泛应用于国内外油气田[1-6],非常适合处理带有压缩机停机、单井注气压力限制等复杂因素的注气速度优化问题。
1 限制性条件
Ray在2007年就对气举最佳注气速度的优化问题进行了分析[7]。但他没有考虑压缩机容量的限制问题,而且使用Ray的方法必须事先知道总的可注入气举气量。本文在Ray的研究基础上,把压缩机容量限制作为一个重要前提,并对各单井注气量进行拟合,从而预测总的气举可注入气量。
1.1 单井动态曲线拟合
近些年来,单井气举研究取得了长足发展[8-11]。获取单井特征曲线的方程表达式是确定气举操作区间的关键,按照Ray的方法,单井特征曲线可由幂函数f(Qg)来计算:
Qo=f(Qg)
(1)
式中:Qg为单井注气量,104m3d;Qo为单井产油量,m3d。
f(Qg)的次数由该井特征曲线的拟合情况来确定。Ray方法要求的可注入气举总气量可由单井所需注气量加和得到。这里使用气举软件(如Pipsim软件)对单井模拟模型进行敏感性分析并得到各注气量下的产油量,从而绘出气举特性曲线,然后再用幂函数f(Qg)对气举特性曲线进行拟合。图1是对海上某油气田X-01井模拟模型进行敏感性分析后得到的气举特性曲线。由图1可知,对于X-01井来说,五次方程能很好地对其气举特性曲线进行拟合, 故f(Qg)的次数为5。
在图1中,气举操作区间由2条垂直线(L1和L2)来界定,低于区间的下界时生产井不稳定,高于区间的上界时会导致产量下降。操作区间的上界(L2)就是X-01井的技术最优生产点。

图1 X-01井的气举特性曲线
1.2 目标函数与限制条件
将所有井的特征曲线拟合函数fi(Qgi)计算得到的产量相加得到总产量,然后将总产量取最大值作为目标函数,如公式(2)所示:
(2)
根据单井注气速度Qgi应处于气举操作区间之内这一限制条件,Qgi应满足:
Qgimin≤Qgi≤Qgimax
(3)
同时,把压缩机容量限制作为一个重要前提,即所有井的总注气量不能大于压缩机系统用于气举的最大输气量:
(4)
式中:Qo为总产量;Qgimax指i井的最大气举注气量;Qgimin指i井的最小气举注气量;若openi等于1则表明井是在生产;若openi等于0则表明井是关闭的。
2 优化气举遗传算法
由于每个配气方案包含所有注气井的全部相关参数,利用枚举法不可能详尽评估所有可能的解决方案,遗传算法等搜索方法的目的就是减少评估次数,从而快速找到足够接近全局最优的配气方案[12-13]。
根据图2所示的结构示意图,遗传算法可用来解决上述具有苛刻压缩机能力极限限制的气举优化问题。
2.1 编码方案与初始群体
与Ray研究相同,把与每一口井注入气相关的参数编成染色体字符串,染色体的长度等于井的数目。每口井气举注入速度必须在气举生产区间内,并且通常注气速度不接近零。受到达尔文的启发,遗传算法先是生成配气方案问题可能解的种群,然后让种群进行进化,种群规模设置为200个体(每个种群包含200个体,即200个配气方案),每个个体用染色体来表示。

图2 遗传算法结构图
为了产生初始种群,采用等概率分布函数随机产生一组数,这样就产生了一系列包含从0到1之间随机数的向量,向量的长度等于气举井的数量,向量的数目等于种群的大小,这些向量组成了一个大矩阵(种群矩阵),矩阵的每一行对应一个单一的个体。由于是随机产生,种群矩阵具有更大的“生物多样性”。 配气方案中最重要的参数是单井有效气举注气速度,第口井有效气举注气速度Qgi由式(5)表示:
Qgi=Qgimin+ran(Qgimax-Qgimin)
(5)
式中ran函数用来产生0到1之间的随机数。
遗传算法解决气举优化问题虽然没有从数学上确定出达到收敛的平均迭代次数,但通过案例研究发现,遗传不超过200代就收敛到足够接近全局最优的配气方案。
2.2 个体评价
虽然每口井(基因)得到了有效值,但个体本身有可能是无效的,因为所有井的总注气量不能超过压缩机机组的总供气量。如果不满足这个条件,算法就减少其中一口井的注气量,该井新的注气量要是低于自身的最小注气量,这口井就被关闭。基于此原因,个体生成以后必须先对染色体进行解码,解码后由前所述限制条件先行判断,不合格的个体不进入适应度函数计算和评价。然后,算法验证减少后的总注气量是否小于压缩机机组总供气量,如果不能满足这个条件,另一口井的注气量也将被减少。如果所有井经过减少注气量的过程后,单口井的值还是无效的,那么算法将重新回到开始选井阶段。当然,如果总注气量低于压缩机总供气量时,也可以通过相同的过程来增加注气量。经过减少(或增加)单井注气量后得到的一系列有效个体(满足限制条件)组成整个群体,这个过程通常称为均匀随机初始化过程。
适应度函数为每个个体计算适应度Fitness,并以此对每个个体进行排序。遗传算法一般用目标函数来计算适应度。在这里,适应度的函数值等于所有井的总产量。它可以通过气举动态曲线和相关注气量来计算。
(6)
2.3 个体选择
个体选择是一个被动过程,个体生存或繁殖依赖于其应对环境挑战的能力 —— 基因特征。选择过程是一个长期反复试误并积累优点的过程,其目的是选择优良个体组为以后交叉繁殖后代做准备。有很多种方法来选择个体组,传统的方法是通过轮盘赌来选择。这种方法首先利用适应度函数来评价个体,得到的适应度值必须进行归一化处理,这样所有适应度函数值之和就等于一,然后对个体按照其适应度值的高低进行降序排名,每个个体适应度值决定了个体的繁殖概率,最后将每个个体的归一化后适度值累加起来组成轮盘。传统的方法在处理情况简单、个体适应度差异大的种群时效果较好,但气举配气优化问题在加入限制条件后情况较复杂,为了保证个体的多样性,在计算时往往设置很大的备选种群的规模,如此个体适应度之间的差异开始变小(如图3(a)),这样极大影响了计算收敛速度。为了提高收敛速度,这里采用A Morales等人的MiniVar方法对轮盘赌选择进行改进[14-15]。
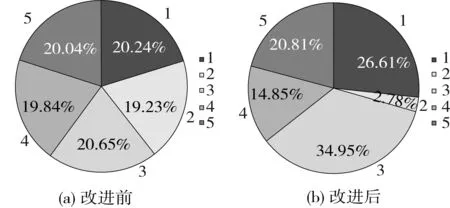
图 3 轮盘赌对比图
首先对初始的适度值数据进行均值和标准方差计算,以此创建一个标准正态分布种群,并获取各个体新的适度值数组:
(7)
式中:x(i)代表i个体的初始适度值,μ和σ表示初始适度值的均值和标准方差,Np代表种群规模。
然后再用高斯误差函数erf()对新的适度值数组进行处理:

(8)
式中μ0和σ0表示各个体新的适度值数组的均值和标准方差。
经过MiniVar改进的轮盘赌适度值分布如图3b所示。两图对比可以看出,图3a中的个体2(占比例最小)与其他个体相比所占比例差距不大,在轮盘赌中很难把个体2淘汰出局。经过改进后在图3(b)中,个体2所占比例大大缩小,这就使个体2被选中的几率大大降低,从而使计算的整体收敛速度大大提高。
2.4 交叉操作
接下来就要对新种群中选出的2个个体进行交叉操作,一般的交叉方法有单点交叉、两点交叉、多点交叉、均匀交叉、融合交叉,方法不同则效果不同。本文采用如图4所示的单点交叉方式, 交叉点随机产生。交叉操作要在一定的概率下进行,这个概率称为交叉率,一般设置为0.5~0.95。按照单点交叉要求,将父代中所有的个体,进行两两交叉。如图4(a)所示,需要随机选定一个位置作为交叉点,将2个个体划分成2部分,相互交换后半部分,分别得到2个新的个体。

图4 交叉运算与变异运算
2.5 变异操作
从父代中随机选择的个体要进行变异操作。变异就是对染色体的结构进行变异,使其改变原来的结构(值也就改变),达到突变进化的目的。通过变异可以把搜索范围扩大到初始种群产生的基因组合之外。这也减少了收敛到局部最优的概率。变异操作也要遵从一定的概率来进行,一般设置为0~0.5。如果变异的概率是0.25,那么将有四分之一的个体将进行变异。
如图4(b)所示,选定一个随机位置,翻转该位置的二进制字符,从而得到一个新样本。
本文的变异方法直接采取基因位反转变异法,即0变为1,1变为0。要进行变异的基因位的选取也是随机的。
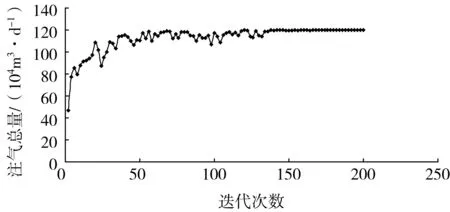
图5 优化计算迭代过程图
传统遗传算法是在每次迭代后保持种群个体数量恒定,按照这种方法,新产生的个体数量等于上一代的个体数量(完全取代)。本文对传统遗传算法进行细微的修改,即以前最好的个体组的一小部分(20%)被保持到下面的迭代过程。这保证了下一代最佳个体不比上一代最佳个体差。新算法可以减少收敛时间和加快优化过程。
3 设计实例
在此运用遗传算法对中国海上某油气田的11口井进行气举优化。为得到各口井的特征曲线,应用气举软件对这些井进行气举敏感性分析,其中一口井(X-01)的特征曲线见图1。
考虑到气体输出及电力条件问题,浮式生产储油系统配备了2个压缩机组,2个机组并行时,总排气量约120×104m3d。遗传算法参数设置如下:编码长度为15;种群规模为200;选择方式为轮盘赌(MiniVar);交叉类型为单点交叉;交叉概率为0.5;变异概率为0.1;迭代终止次数设置为500。
图5是利用种群中所有个体目标函数的平均值绘出的优化计算迭代过程图。由图5可以看出,迭代次数初步设置为500次,但实际计算显示遗传不超过200代计算程序就开始收敛到足够接近全局最优的配气方案。
表1反映出各井配气及产量情况。可以看出,由于所研究的井都需要气举来维持产量, X-04井和X-09井气举速度较小,相对于其他井而言效益较低而被关闭。由表1中的实际产油量和设计产油量对比可以看出,两者大体一致。这验证了遗传算法最基本的特点:虽然无法找到这种问题的全局最优解,但能找到可以接受的全局次优解。

表1 各井配气及产量表
4 结 语
(1)在考虑单井注气速度应处于气举操作区间和总注气量必须不大于压缩机总容量等限制条件的情况下,运用改进的遗传算法能够选择关闭井以及井的关闭顺序。
(2)在遗传算法选择个体的过程中,本文采用A Morales等人的MiniVar方法对轮盘赌进行了改进,从而极大地提高了遗传算法的收敛速度。
(3)改进后的遗传算法在处理带有压缩机停机、单井注气压力限制等复杂因素的注气速度优化问题时,虽然无法找到全局最优解,但能找到可以接受的全局次优解。
[1] 崔智敏,王银凤.基于遗传算法的油田注水系统运行优化研究[J].科学技术与工程,2012,12(7):1656-1658.
[2] 黄辉,吴晓东,孙天礼.基于遗传算法的低渗透气藏水平井压裂参数优化[J].天然气工业,2008,28(5):91~93.
[3] Qin Lu,Graham C Fleming.The Optimization of Continuous Gas Lift Process Using an Integrated Compositional Model[G].SPE 140935,2011.
[4] Sharifa Al-Ruheili,Mathew Angelatos,Sujith Nair,et al.Production Optimization and Zonal Allocation for Auto Gas Lift Wells:A Case Study from Oman[G].SPE 161648,2012.
[5] Artur Posenato Garcia,Vinícius Ramos Rosa.A Genetic Algorithm for Gas Lift Optimization With Compression Capacity Limitation[G].SPE 153175,2012.
[6] Pierre Samier.Comparisons of Various Algorithms for Gas-Lift Optimization in a Coupled Surface Network and Reservoir Simulation[G].SPE 130912,2010.
[7] Ray T,Sarker.R.Genetic Algorithm for Solving a Gas Lift Optimization Problem[J].Journal of Petroleum Science and Engineering,2007,59:84-96.
[8] 于淑珍,胡康,冯朋鑫,等.一种井间互联气举排水采气新方法[J].特种油气藏,2013,20(4):138-140.
[9] 李华锋,王庆,冯祥.考虑井筒压降的水平井流速及压力分布研究[J].断块油气田,2011,18(3):366-368.
[10] 张林,熊友明.水平井筒油水两相流压降计算模型[J].断块油气田,2009,16(5):77-80.
[11] 杨帆.气井多相垂直管流段压力损失敏感性分析[J].特种油气藏,2008,15(5):63-65.
[12] 钟海全,李颖川,刘永辉.用混合罚函数法求解气举区块优化配气模型[J].石油学报,2007,28(1):146-150.
[13] 罗银富,黄炳光,王怒涛,等.改进的非支配排序遗传算法优化气举配气[J].西南石油学院学报,2009,31(2):64-66.
[14] Morales A,Nasrabadi H,Zhu D.A Modified Genetic Algorithm for Horizontal Well Placement Optimization in Gas Condensate Reservoirs[G].SPE 135182,2010.
[15] Morales A N,Nasrabadi H. Zhu D.A New Modified Genetic Algorithm for Well Placement Optimization under Geological Uncertainties[G].SPE 143617,2011.

