Wilcoxon秩和检验在热带气旋强度预报方法评定中的应用

周聪，余晖，傅刚

(1．中国海洋大学海洋环境学院，山东青岛266100;2．中国气象局上海台风研究所，上海200030)

0 引言

热带气旋(tropical cyclone，简称TC)强度变化的研究和预报历来受到重视(于润玲等，2013)。目前国内外常见的热带气旋强度预报方法主要有数值预报方法和统计预报方法。研究表明，数值预报对TC路径预报效果较好，而统计预报对TC强度预报的优势较明显(汤杰等，2011)。在对TC强度业务预报的精度进行评定时，一般考虑TC强度的平均绝对误差、预报趋势一致率、均方根误差、箱线图和技巧水平等指标(占瑞芬等，2010;汤杰等，2011)。

在TC强度的业务预报上，除了关注上述指标外，往往还需要知道TC强度预报的显著性检验结果。从统计的角度看，由于对TC强度预报精度评定时所考虑的样本总体分布是非正态分布，所以在显著性检验时不能直接利用常规的t、F等参数检验方法，而应先对样本采取正态化转换，或者使用简单有效的非参数检验法。事实上，气象统计样本总体分布往往是非正态分布，或仅满足局部正态分布(Gunn and Marshall，1958;White，1980;Ulbrich，1983;Birmili et al．，2001)，因此研究非参数检验法在气象上的应用具有十分重要的科学意义和实用价值。气象上常见的非参数检验方法是蒙特卡罗检验，在使用蒙特卡罗检验时，为使其统计检验有较高的模拟精度，样本量N需要很大(超过十万甚至上百万)。本文将介绍一种不依赖样本总体分布，且不需要满足大样本条件的非参数Wilcoxon检验法。

目前中国TC强度的业务客观预报方法(中国气象局，2012)有4个:气候持续法模型(余晖等，2006)、统计预报模型(Chen et al．，2011)、遗传神经网络模型(姚才等，2007)、偏最小二乘模型(宋金杰等，2011)。为便于讨论，本文选择两种TC强度业务预报方法进行比较，即:气候持续模型(Climatology and Persistence Scheme，简称CLIPER)和偏最小二乘法(Partial Least Squares Scheme，简称 PLS)。CLIPER于2005年正式投入业务使用，PLS于2010年投入准业务使用。

1 热带气旋强度误差分布

将某一时次的TC强度误差(Error，简称E)定义为

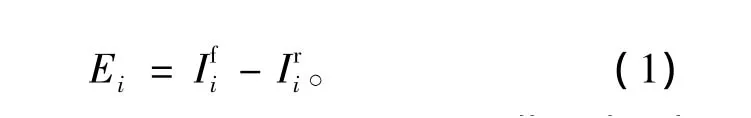
式中:i指第 i个时次样本，i=1，2，…，n;n指预报时次总数;I代表台风强度(以TC近中心最大风速表征);f、r分别代表强度预报模型和实际情形。

计算2005—2012年6月12 h预报时刻 CLIPER模型的预报误差，记为Ei。

将 Ei(i=1，2，…，n)标准化，记为，绘制频率分布，如图1所示，其中x轴表示E(1)i值，y轴表示对应值出现的频数。与标准正态分布曲线(虚线)比较，初步判断的分布是非正态分布。进一步对E(1)i做描述性统计分析，发现其偏度与峰度超过正态分布临界标准(Mardia，1970;Srivastava，1984)，可以判定该数据的总体分布是显著非正态分布。如果对此类对象进行显著性检验，常用的t检验、F检验等参数检验无法使用。

记 Ei(i=1，2，…，n)中位数为 θ，记θ(i=1，2，…，n)，并绘制频率分布，如图 2 所示，其中x轴表示值，y轴表示对应值出现的频数。若将看作近似的对称分布，此时可采取适用于对称分布总体的非参数检验方法。

2 非参数检验法

参数检验指用某些参数(如正态分布中的平均值和方差)来描述总体的特征并对样本所属总体的性质做出若干假设检验，是近代气候学研究中最常用的统计方法。由这类方法导出的结论会受到参数假设的限制。而对参数不作严格的假设，相对于参数检验而言，对资料的分布形态没有特殊的要求或只作一点诸如对称性之类的简单假设，一般称作非参数检验。

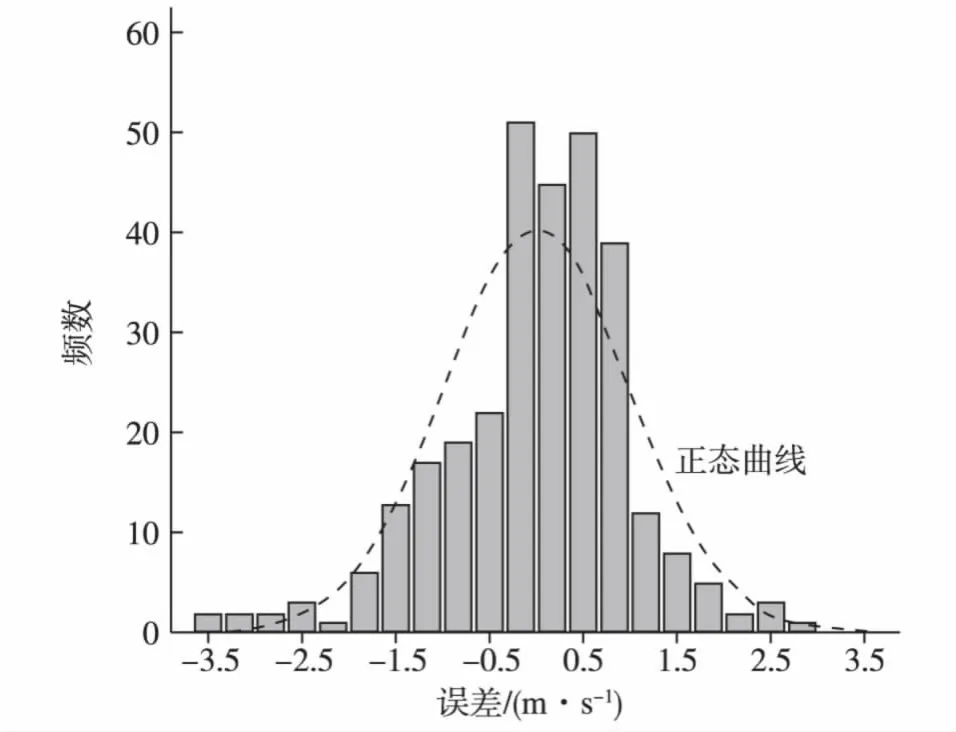
图1 E的频数分布Fig．1 Frequency distribution of E

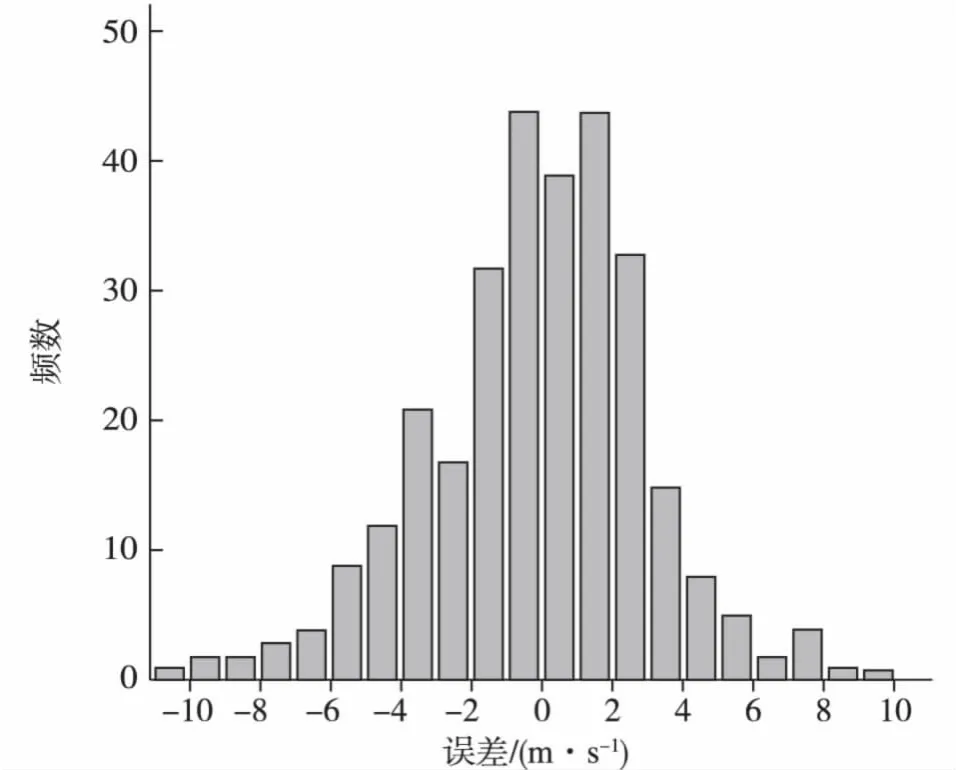
图2 E的频数分布Fig．2 Frequency distribution of E

非参数检验把数据按大小排队，使每个数据都有自己的“地位”，称为秩(Rank)。虽然不知道原始数据的分布形式，但是这些秩及由其产生的一些统计量的性质和分布是可以得到的。吴喜之(2006)研究认为，由这种方法得出的结论更具普遍意义。

常用的非参数统计方法有符号检验、秩和检验、等级相关检验、Mann-Whitney检验，超大样本如气候学研究中常见的蒙特卡罗检验等。在气象学研究中，很多情况下参数检验不适用，这是因为在参数检验中，数据的分布一般默认为正态分布、方差齐性，然而大多数气象数据并不满足此种特征，在这种情况下假如坚持使用参数检验，势必会歪曲数据的本来面目，从而使人们对检验的有效性产生怀疑。

Wilcoxon(1945)针对对称分布提出了一种简单有效的非参数检验方法，在总体分布未知、或者不考虑研究对象具体分布的情况下，非参数检验可以用于研究目标总体与理论总体分布是否相同，或者各样本所在总体的分布位置是否相同(张文彤和闫洁，2004)。Wilcoxon(1945)巧妙地将非参数过程转化为参数过程(Conover and Iman，1981)，该方法在医学统计、生物、行为科学中已有广泛应用(Gehan，1965;Tarone and Ware，1977;蒋知俭，1997;Roth et al．，1998)。

3 Wilcoxon符号秩和检验

在 X1，X2，…，Xn中，Xi如果是第 Ri个最小值，即Xi=X(Ri)(第 Ri个顺序统计量)，称 Ri为 Xi的秩。R统计量只考虑了样本点的大小而未考虑其绝对值的大小，然而其绝对值的大小有时也必须考虑。

Wilcoxon符号秩统计量用W来表示。样本的绝对值|X1|，|X2|，…，|Xn|排序，其顺序统计量为表示|Xj|在绝对值样本中的秩，即，还用S(x)表示符号函数I(x＞0)，它在x＞0时为1，否则为0。Wilcoxon符号秩统计量定义为

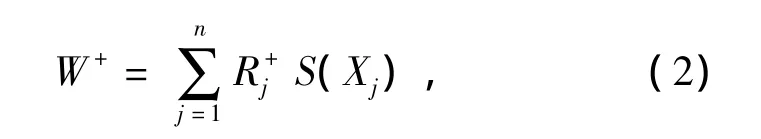
它是正的样本点按绝对值所得的秩的和(Wilcoxon，1945)。

假设F(x－θ)为连续分布的总体，通常零假设为H0:θ=0，按照以上定义，有以下定理:

如果零假设 H0:θ=0成立，则 W1，W2，…，Wn是独立同分布的(吴喜之，2006)，其分布为P(Wi=

用正态近似求W+的分布，则

由中心极限定理，在n大时，可近似地认为

对于上面的正态近似，也可以如下表示，当n很大时，有

以上检验过程不仅适用于单样本，而且可推广到配对样本上(Wilcoxon，1945;吴喜之，2006)。假设(X1，Y1)，(X2，Y2)，…，(Xn，Yn)代表随机抽样的一组配对数据。

令 Pi=Yi－ Xi，Qi=Xi－ Yi(i=1，2，…，n)，根据中位数性质，Pi、Qi的总体也具有连续对称性，设其总体的中位数为 θP、θQ，则原假设 H0:θ1= θ2可替换为H'0:θP=θQ=0，即回归到单样本情形。

在TC强度预报中实现Wilcoxon秩和检验，首先定义误差E1i、E2i:

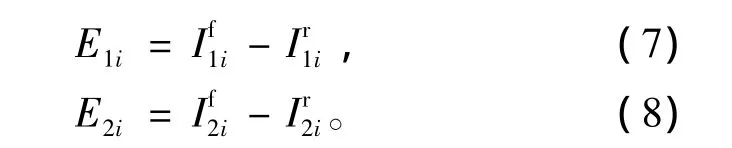
其中:i指第 i个时次样本，i=1，2，…，n;n代表独立样本个数;代表两种台风强度预报方法的预报结果;f、r分别代表强度预报模型和实际情形。

经过整理简化，Wilcoxon符号秩检验在TC强度预报检验中的流程为:

1)令 Wi=E2i－ E1i(i=1，2，…，n)，如果 Wi是正数，记为正号;Wi为负数，记为负号。

2)计算Wi的绝对值。

3)将Wi的绝对值按升序排列，求出相应的秩。

4)分别计算正、负号Wi的秩和，分别记为W+和W－。

若正、负秩总和大致相当，可以认为两配对样本数据正负变化程度基本相当，分布差距较小。

两配对样本的Wilcoxon符号秩和检验，按照下面的公式计算Z统计量，当样本容量足够大时，Z近似服从正态分布。

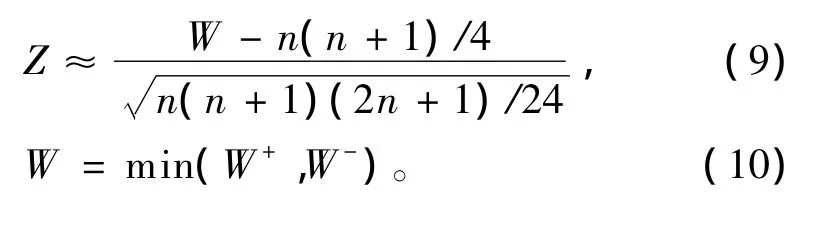
对于单边检验H0:θ=θ0，Hα:θ＞θ0及水平α，W的临界值为

其中:Zα通过查正态分布表获得。若W的计算值超过临界值c，则否定原假设，认为两个样本的分布不同。

分别计算2005—2012年12 h预报时刻下CLIPER模型、PLS模型的预报误差，记 ECLIPERi、EPLSi。根据Wilcoxon秩和检验方法，得到Z统计量超过临界值，拒绝原假设，即认为2005—2012年6月的CLIPER模型和PLS模型在12 h的预报误差存在显著性差异。

4 结论与讨论

TC强度的预报结果与观测结果的误差分布是非正态分布，此时若进行显著性检验，可使用非参数检验方法。作为最常用的非参数检验方法之一，Wilcoxon秩和检验不要求确保样本所属的总体符合某种理论分布，仅需总体具有对称性，具有十分广泛的适用性(吴喜之，2006)。

Wilcoxon秩和检验也可以与其他TC强度预报评定参数相结合，有利于进一步提高当前精度预报水平。然而，该方法也有一定的局限性。在总体分布已知时，相比参数方法，非参数方法无法充分利用样本中信息，因此，在大多情况下参数检验方法仍然是最有效的显著性检验方法。

蒋知俭．1997．医学统计学［M］．北京:人民卫生出版社:168-174．

宋金杰，王元，陈佩燕，等．2011．基于偏最小二乘回归理论的西北太平洋热带气旋强度统计预报方法［J］．气象学报，69(5):745-756．

汤杰，陈国民，余晖．2011.2010年西北太平洋台风预报精度评定及分析［J］．气象，37(10):1320-1328．

吴喜之．2006．非参数统计［M］．北京:中国统计出版社:23-25;32-41．

姚才，金龙，黄明策．2007．遗传算法与神经网络相结合的热带气旋强度预报方法试验［J］．海洋学报，29(4):11-19．

余晖，胡春梅，蒋乐贻．2006．热带气旋强度资料的差异性分析［J］．气象学报，64(3):357-363．

于润玲，余晖，端义宏．2013．登陆华南热带气旋强度变化与大尺度环流的关系［J］．大气科学学报，36(5):619-625．

占瑞芬，汤杰，余晖．2010.2009年西北太平洋热带气旋定位和业务预报精度评定［J］．气象，36(10):114-121．

张文彤，闫洁．2004．SPSS统计分析基础教程［M］．北京:高等教育出版社:279-301．

中国气象局．2012．台风业务和服务规定［S］．北京:气象出版社．

Birmili W，Wiedensohler A，Heintzenberg J，et al．2001．Atmospheric particle number size distribution in central Europe:Statistical relations to air masses and meteorology［J］．J Geophys Res，106(D23):32005-32018．

Chen P Y，Yu H，Chan J C．2011．A western North Pacific tropical cyclone intensity prediction scheme［J］．Acta Meteor Sinica，25:611-624．

Conover W J，Iman R L．1981．Rank transformations as a bridge between parametric and nonparametric statistics［J］．Am Stat，35(3):124-129．

Gehan E A．1965．A generalized two-sample Wilcoxon test for doubly censored data［J］．Biom，52(3/4):650-653．

Gunn K L S，Marshall J S．1958．The distribution with size of aggregate snowflakes［J］．J Meteor，15(5):452-461．

Mardia K V．1970．Measures of multivariate skewness and kurtosis with applications［J］．Biom，57(3):519-530．

Roth J A，Atkinson E N，Fossella F，et al．1998．Long-term follow-up of patients enrolled in a randomized trial comparing perioperative chemotherapy and surgery with surgery alone in resectable stage III:A non-small-cell lung cancer［J］．Lung Cancer，21(1):1-6．

Srivastava M S．1984．A measure of skewness and kurtosis and a graphical method for assessing multivariate normality［J］．Stat Probabil Lett，2(5):263-267．

Tarone R E，Ware J．1977．On distribution-free tests for equality of survival distributions［J］．Biom，64(1):156-160．

Ulbrich C W．1983．Natural variations in the analytical form of the raindrop size distribution［J］．J Climate Appl Meteor，22(10):1764-1775．

White G H．1980．Skewness，kurtosis and extreme values of Northern Hemisphere geopotential heights［J］．Mon Wea Rev，108(9):1446-1455．

Wilcoxon F．1945．Individual comparisons by ranking methods［J］．Biometrics Bull，1(6):80-83．