Reliability Study on the Risk Precontrol Management System of Coal Mines Safety
SUN Qing (孙 青)
1 Postdoctoral Work Station, Shenhua Group Corporation Limited, Beijing 100011, China 2 Postdoctoral Mobile Research Station, China University of Mining and Technology, Beijing 100083, China
Reliability Study on the Risk Precontrol Management System of Coal Mines Safety
SUN Qing (孙 青)1,2*
1PostdoctoralWorkStation,ShenhuaGroupCorporationLimited,Beijing100011,China2PostdoctoralMobileResearchStation,ChinaUniversityofMiningandTechnology,Beijing100083,China
Risk precontrol management system of coal mines safety (RPMSCS) provides a set of preventive safety management strategy for high-risk coal industries, which has captured extensive attentions. Fundamentally, there are several membership systems with subsystems in the management system, and the subsystem reliability has an important influence on the management system performance. Through analyzing the structure characteristics of the management system, the phase type distribution was employed to analyze its subsystem reliability by considering repair process and three states including working, fail-abnormal, and fail-emergency states. The reliability indices of the subsystem were derived respectively, including the probabilities that the subsystem in three states, mean time to the first failure, mean time to first fail-emergency, mean working time to first fail-emergency, and mean maintenance time to the first fail-emergency, are derived respectively. The probabilities of the membership systems and the management system in three states were also derived. Some numerical examples were used to show the procedures. The result is important for better understanding the management system operation and improving its operational performance from the respect of system reliability.
safetymanagement;riskprecontrolmanagementsystem;systemmodeling;phasetypedistribution;systemreliability
Introduction
As the leader of R&D units of the risk precontrol management system of coal mines safety (RPMSCS) system, industry’s giant Shenhua Group vigorously implements the RPMSCS system in the range of the group. In 2012, the State Council of China organized the National Coal Mine Production Safety Experience Sharing Forum in Shenhua Ningxia Coal Industry Group to promote Shenhua’s safety management experience, and it pointed out that one of the Shenhua’s most important safety management lessons is constructing the RPMSCS system.
Analyses on the topic of RPMSCS system recently appeared a lot. Chen advised adopting hazards identification and risk analysis to form a standardized self-management mechanism[1]. Shuetal. proposed the risk pre-control management information system to realize effective management for the risk of coal mine safety[2]. Hao systematically studied the RPMSCS system including planning and establishment, processes and methods, safeguard and supervisory mechanism, and the control methods for the unsafe behavior[3-4]. Zhang proposed a theoretical model of coal mine accident causation based on summarizing the characteristics of hazard sources and failure modes in coal mines[5]. The similarity of the above researches is all of them trying to improve the safety management level of coal mine by their studies; however, all of them ignore the study on the RPMSCS system reliability. The more complicated system is, the greater its demand for reliability is. If the RPMSCS system reliability can’t reach the requirement, the possibility of the RPMSCS system failure and the loss will increase.
Although researches on the reliability of the RPMSCS system can be rarely found, lots of papers on the complicated system can be easily obtained, which are valuable in enriching the research approaches. Geraedetal. presented a low-cost, compositional approach based on the use of the first four statistical moments to characterize the failure time distributions of the constituent components, subsystems, and top-level system[6]. Hawkesetal. studied the iron channel characteristics and the achievement they obtained held an important place in the research including system reliability, stochastic process, and aggressive Markov process[7-8]. Tianetal. presented a new method considering different meanings of probability interval to calculate uncertainty importance[9]. Deliaetal. studied a two-unit cold standby system under the assumption of the random operational and repair times following phase type distributions[10].
Based on the research above, this paper analyzes the structural relationships among the RPMSCS system, its membership systems, and the subsystems of the membership systems, and employs the phase type distribution to analyze its subsystem reliability by considering repair process and three states including working, fail-abnormal, and fail-emergency states. The reliability indices of the subsystem are derived respectively, including the probabilities that the subsystem in three states, mean time to the first failure, and mean time, mean working and mean maintenance time to the first fail-emergency. The probabilities of the membership systems and the RPMSCS system in three states are also derived. This study will help us to better understand the RPMSCS system and improve its operational performance.
1 Models and Assumptions
1.1 Structural analysis of the RPMSCS system
RPMSCS was creatively established in 2011, based on summarizing the experience and lesson of the safety management practice of the coal industry of China. By analyzing the structural characteristics of the RPMSCS system, we can find that RPMSCS system is composed of six membership systems: risk precontrol management system, guarantee management system, unsafe behavior management system, safety factors management system, comprehensive management systems, and evaluation management system. And each of these membership systems consists of several subsystems. Taking the risk precontrol management system for example, this membership system has hazard identification subsystem and other six subsystems. More details about the RPMSCS system, its membership system and the subsystems of the membership system, can be found in Ref. [4]. In this paper, we will directly use the number of the subsystems of each membership system to calculate the related indices.
From the respect of system reliability, we also can find that: firstly, to stress the strict reliability requirement, the RPMSCS system is the series system consisting of the six membership systems; secondly, for each membership system having finite subsystems, if some of them maintain high reliability, the corresponding membership system will maintain high reliability as well; thirdly, the number of the subsystems may change by considering management condition changes. In this paper, we deem that the subsystems of each membership system are connected inkout ofn:G.
As shown in Fig.1, the RPMSCS system considered here consists of the above mentioned six membership systems connected in series, with the membership system consisting of the corresponding number subsystems inkout ofn:G. So, if the reliability indices of the subsystem can be obtained, we will get the RPMSCS system reliability indices.

Fig.1 The demonstration of the RPMSCS system
In this paper,si(i=1, 2, …, 6) represents the membership systemi,sijrepresents the subsystemjof the membership systemi, andki(i=1, 2, …, 6) means the minimal number of the subsystems to make the corresponding membership systemiwork.Wrepresents working state,FArepresents fail-abnormal state,FErepresents fail-emergency state,MTTFFis the mean time to the first failure state, andMTTFFEis the mean time to the first fail-emergency state.
1.2 Assumptions of the subsystem model
To better illustrate the model, the assumptions of the subsystem are as follows.
(1) At the beginning, each subsystem is new, and it has three states:W,FA, andFE.
(2) Each subsystem lifetime distribution obeys the same phase type distribution.
(3) If the subsystem doesn’t work at timeTi, the subsystem will enter into the fail-abnormal stateFAiwith probabilityui, and into the fail-emergency stateFEwith probability 1-ui.
(4) When the subsystem enters into the fail-abnormal stateFAiat timeTi, the minimal repair actions will be adopted by
considering prudent repair strategy, and the repair time of the system obeys the exponential distribution with parameterυi.
(5) When the subsystem enters into the fail-emergency stateFEat timeTi, no repair action will be adopted by considering prudent repair strategy.
(6) When the subsystem adopts the repair actions at timeTi, the system will return back to the working stateWiwith probabilityβiby considering the possible practical management limitations, and enter into the fail-abnormal stateFAi+1with probability 1-βiuntil timeTn-1.
Based on the above assumptions, the state transition diagram of the subsystem can be precisely modeled, as shown in Fig.2. There arenworking states,nfail-abnormal states, and one fail-emergency state.

Fig.2 The state transition diagram of the subsystem
2 Reliability Indices of the System
2.1 Analysis of the subsystem states
Based on the above assumptions, the subsystem states can be described by the Markov process. By considering fail-abnormal and fail-emergency, we divide the space of the subsystem states into three subsets:W,FA, andFE, where subsetWconsists of all the working states, subsetFAconsists of all the fail-abnormal states, and subsetFEconsists of the fail-emergency states. Obviously, the subsystem generator matrixQcan be separated as

(1)
And the expression ofQWW,QWFA,QWFE,QFAW, andQFAFAcan also be obtained


AndQFAFE=QFEW=QFEFA=QFEFE=0.
2.2 The reliability indices of the system
Based on the related reliability theory and previous researches, we can obtain the following reliability indices of the subsystem.
(1) LetQFAW=0, andQFAFA=0, a new Markov model will be obtained. By solving the corresponding differential equations with initial conditionP(0), we will get the reliabilityR(t), the fail-abnormal probabilityPFA(t), and the fail-emergency probabilityPFE(t) of the subsystem.
(2) If we re-divide the space of the subsystem states as

We will getFT(t)=1-P(0)eQRARAtI, whereIis the column vector of ones. Then we can get the subsystem’s mean time to the first fail-emergencyMTTFFEfrom the formula

(2)
(3) By separatingMTTFFE, we will get the subsystem’s mean working time (MWTTFFE) and mean maintenance time (MMTTFFE) to the first fail-emergency state.
From Fig.1, we can find that the subsystems of the membership systemsi(i=1, 2, …, 6) are connected inkout ofn∶G. And based on previous researches, the reliability indices of the membership systemsi(i=1, 2, …, 6) can be obtained as follows.
(4) The working probability is, when at leastkisubsystems are in working state:
(3)
(5) The fail-emergency probability is, when at leastni-ki+1 subsystems are in fail-emergency state:
(4)
(6) The fail-abnormal probability is, when the membership systemsiis in neither working nor fail-emergency state,

(5)
As shown in Fig.1, the membership systems of RPMSCS system are connected in series. And based on previous studies, we can get the following reliability indices of RPMSCS system.
(7) The working probability is, when all the six membership systems are in working state:

(6)
(8) The fail-emergency probability is, when at least one membership system is in fail-emergency state:

(7)
(9) The fail-abnormal probability is, when the RPMSCS system is in neither working nor fail-emergency state,
(8)
3 Numerical Examples
For simplicity, we assume that the subsystem has two working states, and the parameters of the subsystem areλ1, 2=2,λ1, 3=2,λ2, 4=5,u1=0.5,u2=0.6,β1=0.5,υ1=2,β2=1,υ2=1, andki=ni-1, wherekimeans the minimal number of the subsystems to make the corresponding membership systemsiwork, andniis the number of the subsystems of the membership systemsi. Based on the study above, the generator matrix of the subsystem is

(1) By using Maple, we can get that the reliability of subsystem isR(t)=3e-4t-2e-5t, and mean time to the first failure of the subsystem isMTTFF=7/20. The probabilities of the subsystem in the fail-abnormal and fail-emergency states arePFA(t)=0.55-7/4·e-4t+6/5·e-5tandPFE(t)=0.45-5/4·e-4t+4/5·e-5t, respectively.
(2) By using Maple, we can find that the subsystem’s mean time to the first fail-emergency state isMTTFFE=2, and the subsystem’s mean working time and mean maintenance time to the first fail-emergency state areMWTTFFE=9/14 andMMTTFFE=19/14, respectively.
(3) For the derived expressions of the working, fail-abnormal and fail-emergency probabilities of the six membership systems and the RPMSCS system by Maple are too complicated. Here, we use the figures to show the results. Figures 3-5 show the results of the six membership systems, and the results of the RPMSCS system are shown in Fig.6.

Fig.3 R(si)(t) of six membership systems
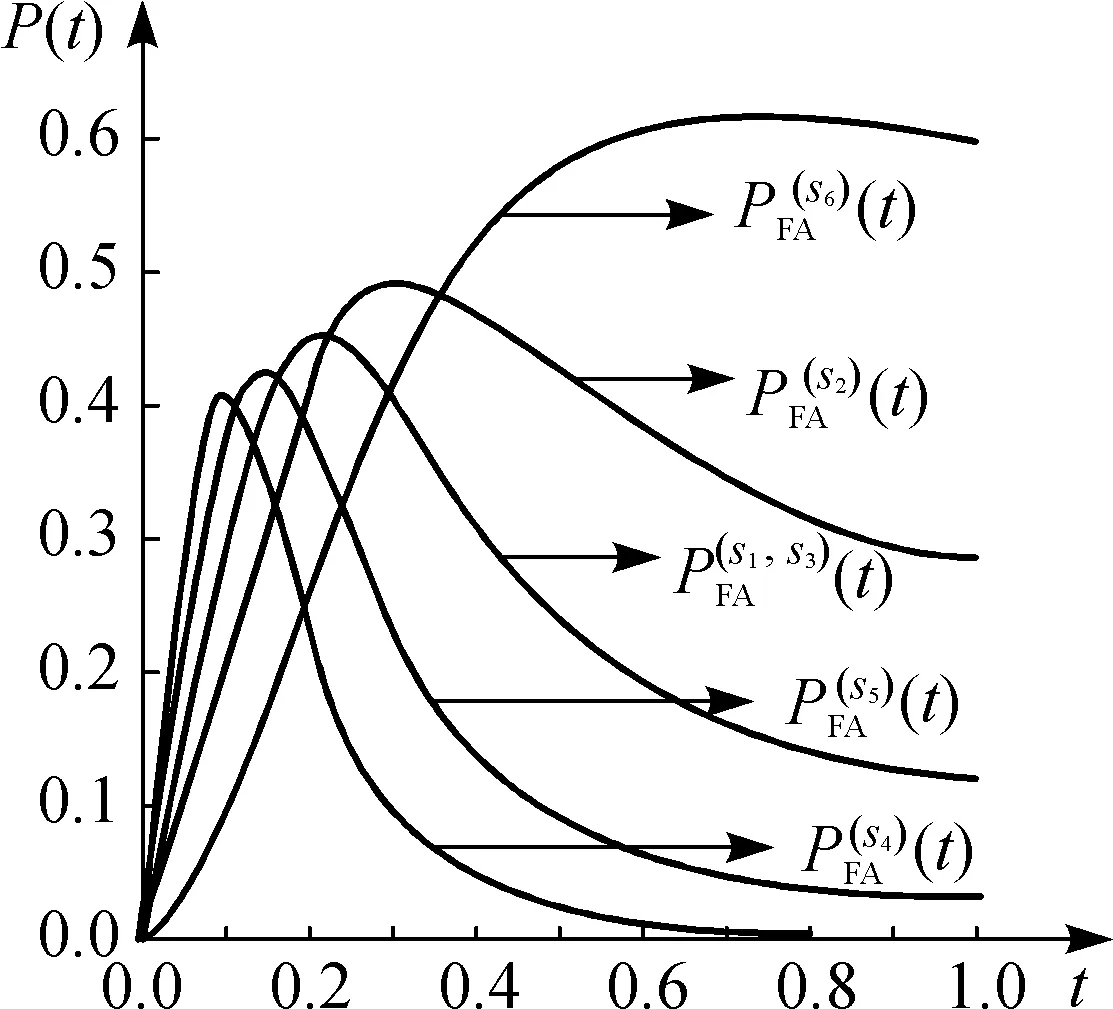
Fig.4 (t) of six membership systems
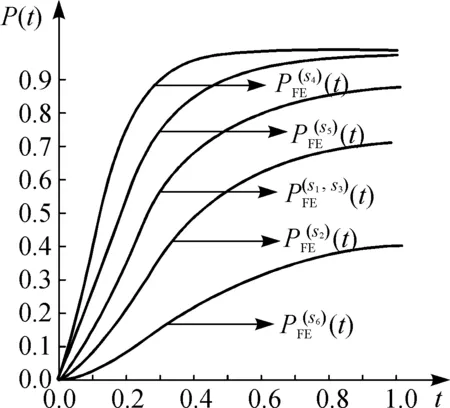
Fig.5 (t) of six membership systems

Fig.6 Reliability indices of RPMSCS system
4 Conclusions
Practice proves that the RPMSCS system is an effective system to improve the safety management level of the high-risk coal industry.In 2012, State Production Commission of State Council of China issued a special document to promote Shenhua’s experience in safe production. Based on analyzing the structure characteristics of the RPMSCS system from the respect of system reliability, lots of system reliability indices are derived. Our formulas have significant meanings for deeper understanding the RPMSCS system operation and improving its operational performance from the respect of reliability. The extension can be made by considering general form of lifetime distribution, maintenance strategy,etc.
[1] Chen W M. Coal Mine Intrinsic Safety Management Based on Rrisk Precontrol [J].ChinaSafetyScienceJournal, 2007, 17(7): 59-62.(in Chinese)
[2] Shu L C, Zhang C. Risk Precontrol Management Information System of Coal Mine Safety [J].IndustryandMineAutomation, 2011, 4: 18-22.(in Chinese)
[3] Hao G. Risk Precontrol Management is the Optimal Method for Hidden Danger Check and Control [J].ChinaCoal, 2011, 37(12): 86-88.(in Chinese)
[4] Hao G. Risk Precontrol of Safety in Coal Mine [M]. Beijing: China Coal Industry Publishing House, 2013: 48-52. (in Chinese)(in Chinese)
[5] Zhang J M. Coal Mine Accident Causation Theory and Safety Management Measures [J].ChinaCoal, 2013, 39(6): 93-97.(in Chinese)
[6] Geraed L R, Arjan J CV G. Reliability Analysis of Hierarchical Systems Using Statistical Moments [J].IEEETransactionsonReliability, 2007, 56(3): 525-533.
[7] Colquhoun D, Hawkes A G. On the Stochastic Properties of Single Ion Channel [J].ProceedingsoftheRoyalSocietyofLondon.SeriesB,BiologicalSciences, 1981, 211(1183): 205-235.
[8] Colquhoun D, Hawkes A G. On the Stochastic Properties of Burst of Single Ion Channel Opening an of Clusters of Bursts [J].PhilosophicalTransactionsoftheRoyalSocietyofLondonSeriesB-BiologicalSciences, 1982, 300(1 098): 1-59.
[9] Tian H, Chen B Z, Wu Q,etal. Reliability Analysis With Uncertainty of Multistate System[J].SystemsEngineeringandElectronics, 2001, 23(4): 99-102.(in Chinese)
[10] Delia M C, Rafael P A. Deteriorating Two-System with Two Repair Modes and Sojourn Times Phase-Type Distributed [J].ReliabilityEngineeringandSystemSafety, 2006, 91(1): 1-9.
1672-5220(2014)06-0886-04
Received date: 2014-08-08
*Correspondence should be addressed to SUN Qing, E-mail: hhgsunqing@163.com
CLC number:X913.4 Document code: A
 Journal of Donghua University(English Edition)2014年6期
Journal of Donghua University(English Edition)2014年6期
- Journal of Donghua University(English Edition)的其它文章
- Stress-Strength Structural Reliability Model with a Stochastic Strength Aging Deterioration Process
- Settlement Prediction of Dredger Fill with the Optimal Combination Model
- Condition-Based Maintenance Decision-Making for Equipment
- Identification of the Credit Guarantee Network of Steel Trade Enterprises in China
- Methods for Reliability Assessment under Irregular Time-Varying-Stress Degradation Testing
- Efficient Method for Accelerated Reliability Qualification Testing
