Electric Multiple Unit Bogie Maintainability Allocation with Interval Analysis and Fuzzy Evaluation Method

LI Yong-hua(李永华), YU Hong-jie(禹红杰)

School of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116 028, China

Electric Multiple Unit Bogie Maintainability Allocation with Interval Analysis and Fuzzy Evaluation Method

LI Yong-hua(李永华)*, YU Hong-jie(禹红杰)

SchoolofTrafficandTransportationEngineering,DalianJiaotongUniversity,Dalian116 028,China

Based on the failure rate and design features allocation method, considering the multiple influential factors which affect electric multiple unit (EMU) bogies, maintainability allocation on EMU bogie was presented by interval analytic hierarchy analysis and fuzzy comprehensive assessment. The maintainability allocation model was established. Weight based on the influence degree of each factor on maintenance was assigned. Fuzzy interval numbers were used to substitute real numbers and express uncertain information. The maintenance weighting factors for each subsystem were calculated by fuzzy comprehensive assessment. Then the allocation method was applied to EMU bogie. The results show that the method is feasible. The problem difficult to quantify for EMU bogie maintenance allocation is solved effectively.

MaintainabilityAllocation;IntervalAnalysis;FuzzyComprehensiveEvaluation;Bogie

Introduction

Maintainability allocation is assigned the maintenance index to various parts of the various functional products, and insures the functional products meet the quantitative requirements on maintainability[1]. In the maintainability allocation schemes, only one or two factors considered apparently can’t reflect the actual situation. This could lead to unreasonable allocation results. The weighted allocation method based-on failure rate and design features may consider a variety of flexible factors. However, it is not quite reasonable to equally distinguish various factors and their influence levels. And the various factors need to be given directly. Actually, it is difficult to use an accurate number expressing the certain factors.

To solve the above-mentioned problems, it is necessary to resolve the factors uncertainties of influence level and various values for a subsystem. The uncertainties are usually solved by expert marking[2]. However the view of expert is ambiguous in nature. The results should not be judged solely by real numbers. So Ref. [3] put forward the integrated interval analysis with fuzzy analytic hierarchy process (AHP) method which might solve fuzzy problems effectively. The paper uses interval AHP and fuzzy comprehensive assessment method based-on the failure rate and design features allocation[4]to carry out maintainability allocation of electric multiple unit (EMU) bogie.

1 Maintainability Allocation Model

When weighting factor allocation method which integrates the failure rate with design features is presented to allocate maintainability index, the factors of complexity, testability, accessibility, exchangeability, scalability and maintainability are considered. Maintenance parameter mean time to repair (MTTR) is selected. The maintainability allocation model is:

whereTCTis MTTR of the system,TCTiis MTTR of the subsystem,kiis weighting factor,λiis failure rate of subsystem,nis the subsystem number.

Ifk1∶k2∶…∶kn=b1∶b2∶…∶bn,TCTican be converted as:

wherebiis the ratio coefficient of maintenance weighting factor for each subsystem.

wherebjis the ratio coefficient of maintenance weighting factor for subsystem, and ∘ is fuzzy arithmetic operators[6].

2 Maintainability Allocation for EMU Bogie

2.1 Determining the maintainability index and subsystem sets

The maintainability index includes selection of the maintenance parameter and maintainability allocation index. In the paper, MTTR is selected as the maintenance parameter. The maintainability index is determined by user based-on the maintenance level of similar products. EMU power bogie concludes wheel, axle box, primary suspension, bogie frame, secondary suspension, drive device, foundation brake rigging. LetIi(i=1, 2, …, 7) symbolize the above subsystems respectively.

2.2 Determining the influence factors and weights of maintainability allocation

In the paper, six uncertainty factors of failure detection and isolation, accessibility, exchangeability, scalability, complexity and maintenance environment are considered in maintainability allocation of EMU bogie.

Because the nature of the experts’ opinion is ambiguous, pairwise comparison of the results should not be a mere form of real numbers. Traditional hierarchy analysis[7]of a 1-9 scale will be extended for the continuous scale from 0 to 9. The experts give pairwise comparison importance values of the various factors. The ratio can be selected according to the actual needs of an arbitrary number of intervals on the scale. Interval judgment matrix is:

where,φijis the ratio of the influencing factorsUiandUj,φij=1/φji, 1≤i≤6, 1≤j≤6.

2.3 Determining the membership matrix of influencing factors

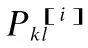
where, 1≤i≤6, 1≤j≤7. The interval number need defuzzificate[8].

Therefore, the maintainability allocation indicators EMU bogie subsystems can be obtained.

3 A Case of EMU Bogie System Maintainability Allocation

Take a power bogie as an example, the main steps of maintainability allocation are as follows.

3.1 Determining the maintainability allocation index

Compared with the similar products maintenance level to determine mean time to repair for the power bogie system isTCT= 3.02 h. It’s about 180 min.

3.2 Determining influencing factor weights of the maintainability allocation

3.3 Determining the membership matrix of factors

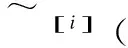
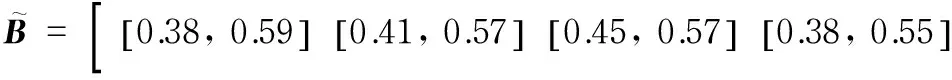
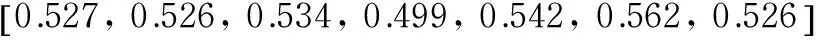
The failure rate of subsystems are known respectively as:

λ1=6.849×10-6,λ2=6.27×10-6,λ3=5.707×10-6.

λ4=4.561×10-6,λ5=2.28×10-6,λ6=5.136×10-6,
λ7=2.905×10-6.

Comparing the maintainability allocation index values of the subsystems with MTTR of the similar existing subsystem, the results are shown in Fig.1. It is a great difference of drive system. So it’s necessary to make maintainability design to lower drive system’s MTTR.

Fig.1 The comparison between maintainability allocation values and existing maintenance levels

4 Conclusions

A variety of design features are necessarily considered in maintainability allocation, and using traditional allocation methods and avaliable data is difficult to quantitative analysis for these features. The interval AHP and fuzzy comprehensive evaluation are applied to establishing maintainability allocation model by weighting factor allocation method which integrated, failure rate with design features.

For evaluation process, interval numbers which are assigned to the interval AHP can make up the stortage of traditional AHP evaluation. It effectively improves the evaluation accuracy.

The proposed method considers a variety of maintainability design characteristics, both the qualitative analysis and quantitative analysis, which has an important referenced value in the actual application. The example results verify the feasibility of the above methods through a system-level power bogie maintainability allocation. In addition, the method can also be applied in the maintenance allocation of other mechanical systems.

[1] Lü C. Design, Analysis and Verification of Maintainability [M]. Beijing: Defense Industry Press. 2012. (in Chinese)

[2] Moore R, Lodwick W. Interval Analysis and Fuzzy Set Theory [J].FuzzySetsandSystems, 2003, 135(1): 5-9.

[3] Hao Q B, Yang Z J, Chen F,etal. A Fuzzy Maintainability Allocation Method for NC Machine Tools Based on Interval Analysis [C]. International Conference on Reliability, Maintainability and Safety, Guiyang, China, 2011: 889-896.

[4] Li C R. Comprehensive Post-Evaluation of Rural Electric Network Reformation Based on Fuzzy Interval Number AHP [C]. Risk Management & Engineering Management, Beijing, China, 2008: 171-177.

[5] Fan L G, Niu D X. An IAHP-Based MADM method in Transmission Network Planning [J].Relay, 2007, 35(12): 47-51.

[6] Wang X F, Wang J Q, Yang W E. General Fuzzy Number Intuitionistic Fuzzy Arithmetic Aggregation Operators Based on Fuzzy Structured Element [C]. Control and Decision Conference, Taiyuan, China, 2012: 2640-2645.

[7] Liang Q W, Jiang S S, Sun T Y. Study on Method of Maintainability Allocation of under Autonomous Water Vehicle Based on Analytic Hierarchy Process [J].FireControlandCommandControl, 2013, 38(7): 115-118. (in Chinese)

[8] Ma M, Kandel A, Friedman M. A New Approach for Defuzzification [J].FuzzySetsandSystems, 2000, 111(3): 351-356.

Traction Power State Key Laboratory of Southwest Jiaotong University, China (No.TPL1 312); Key Project of Technology Research and Development Plan of Railway Ministry, China (NO.2012J009-A); National Natural Science Foundation of Liaoning Province, China (No. 2014028020); Liaoning Province Education Administration Project, China (No.L20138182)

1672-5220(2014)06-0860-03

Received date: 2014-08-08

*Correspondence should be addressed to LI Yong-hua, E-mail: yonghuali@163.com

CLC number: U271.91 Document code: A